Velocity amplification in pressure-driven flows between superhydrophobic gratings of small solid fraction
Abstract
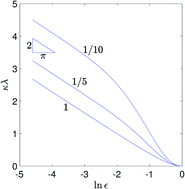
With diminishing fraction of their solid portion, compound gas–solid superhydrophobic surfaces exhibit a large amount of slip which allows for appreciable velocity amplification in pressure-driven microchannel flows. We address this small solid-fraction limit in the context of a grating-like configuration, where superhydrophobicity is provided by a periodic array of flat-meniscus bubbles which are trapped in a Cassie state within the grooved channel walls. Asymptotic analysis for both longitudinal and transverse flows reveals a logarithmic scaling of the effective slip length in the solid fraction of the compound boundaries, thus refuting earlier claims of an algebraic singularity. The logarithmic scaling in the longitudinal problem is explained using an analogy between the unidirectional velocity and the velocity potential in two-dimensional irrotational flows. In the transverse problem it has to do with the Stokes paradox. The mechanisms identified herein explain the absence of slip-length singularity in the comparable asymmetric configuration, where only one of the channel walls is superhydrophobic.


 Please wait while we load your content...
Please wait while we load your content...