Fluctuation tension and shape transition of vesicles: renormalisation calculations and Monte Carlo simulations
Abstract
It has been known for long that the fluctuation surface tension of membranes r, computed from the height fluctuation spectrum, is not equal to the bare surface tension σ, which is introduced in the theory either as a Lagrange multiplier to conserve the total membrane area or as an external constraint. In this work we relate these two surface tensions both analytically and numerically. They are also compared to the Laplace tension γ, and the mechanical frame tension τ. Using the Helfrich model and one-loop renormalisation calculations, we obtain, in addition to the effective bending modulus κeff, a new expression for the effective surface tension σeff = σ − εkBT/(2ap) where kBT is the thermal energy, ap the projected cut-off area, and ε = 3 or 1 according to the allowed configurations that keep either the projected area or the total area constant. Moreover we show that the crumpling transition for an infinite planar membrane occurs for σeff = 0, and also that it coincides with vanishing Laplace and frame tensions. Using extensive Monte Carlo (MC) simulations, triangulated membranes of vesicles made of N = 100–2500 vertices are simulated within the Helfrich theory. As compared to alternative numerical models, no local constraint is applied and the shape is only controlled by the constant volume, the spontaneous curvature and σ. It is shown that the numerical fluctuation surface tension r is equal to σeff both with radial MC moves (ε = 3) and with corrected MC moves locally normal to the fluctuating membrane (ε = 1). For finite vesicles of typical size R, two different regimes are defined: a tension regime for ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) eff = σeffR2/κeff > 0 and a bending one for −1 <
eff = σeffR2/κeff > 0 and a bending one for −1 < ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) eff < 0. A shape transition from a quasi-spherical shape imposed by the large surface energy, to more deformed shapes only controlled by the bending energy, is observed numerically at
eff < 0. A shape transition from a quasi-spherical shape imposed by the large surface energy, to more deformed shapes only controlled by the bending energy, is observed numerically at ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) eff ≃ 0. We propose that the buckling transition, observed for planar supported membranes in the literature, occurs for
eff ≃ 0. We propose that the buckling transition, observed for planar supported membranes in the literature, occurs for ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) eff ≃ −1, the associated negative frame tension playing the role of a compressive force. Hence, a precise control of the value of σeff in simulations cannot but enhance our understanding of shape transitions of vesicles and cells.
eff ≃ −1, the associated negative frame tension playing the role of a compressive force. Hence, a precise control of the value of σeff in simulations cannot but enhance our understanding of shape transitions of vesicles and cells.
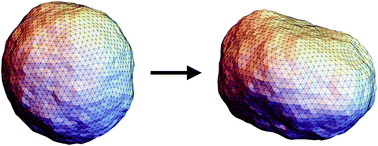


 Please wait while we load your content...
Please wait while we load your content...