Ground state instabilities of protein shells are eliminated by buckling†
Abstract
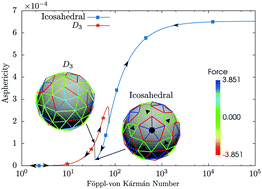
We propose a hybrid discrete–continuum model to study the ground state of protein shells. The model allows for shape transformation of the shell and buckling transitions as well as the competition between states with different symmetries that characterize discrete particle models with radial pair potentials. Our main results are as follows. For large Föppl–von Kármán (FvK) numbers the shells have stable isometric ground states. As the FvK number is reduced, shells undergo a buckling transition resembling that of thin-shell elasticity theory. When the width of the pair potential is reduced below a critical value, then buckling coincides with the onset of structural instability triggered by over-stretched pair potentials. Chiral shells are found to be more prone to structural instability than achiral shells. It is argued that the well-width appropriate for protein shells lies below the structural instability threshold. This means that the self-assembly of protein shells with a well-defined, stable structure is possible only if the bending energy of the shell is sufficiently low so that the FvK number of the assembled shell is above the buckling threshold.


 Please wait while we load your content...
Please wait while we load your content...