Dynamics of Miura-patterned foldable sheets in shear flow
Abstract
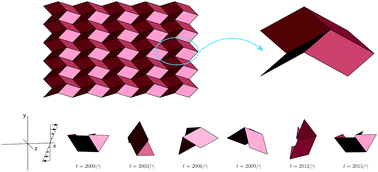
We study the dynamics of piecewise rigid sheets containing predefined crease lines in shear flow. The crease lines act like hinge joints along which the sheet may fold rigidly, i.e. without bending any other crease line. We choose the crease lines such that they tessellate the sheet into a two-dimensional array of parallelograms. Specifically, we focus on a particular arrangement of crease lines known as a Miura-pattern in the origami community. When all the hinges are fully open the sheet is planar, whereas when all are closed the sheet folds over itself to form a compact flat structure. Due to rigidity constraints, the folded state of a Miura-sheet can be described using a single fold angle. The hinged sheet is modeled using the framework of constrained multibody systems in the absence of inertia. The hydrodynamic drag on each of the rigid panels is calculated based on an inscribed elliptic disk, but intra-panel hydrodynamic interactions are neglected. We find that when the motion of a sheet remains symmetric with respect to the flow-gradient plane, after a sufficiently long time, the sheet either exhibits asymptotically periodic tumbling and breathing, indicating approach to a limit cycle; or it reaches a steady state by completely unfolding, which we show to be a half-stable node in the phase space. In the case of asymmetric motion of the sheet with respect to the flow-gradient plane, we find that the terminal state of motion is one of – (i) steady state with a fully unfolded or fully folded configuration, (ii) asymptotically periodic tumbling, indicating approach to a limit cycle, (iii) cyclic tumbling without repetition, indicating a quasiperiodic orbit, or (iv) cyclic tumbling with repetition after several cycles, indicating a resonant quasiperiodic orbit. No chaotic behavior was found.


 Please wait while we load your content...
Please wait while we load your content...