The maximum penalty criterion for ridge regression: application to the calibration of the force constant in elastic network models

Abstract

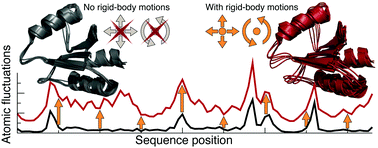
Tikhonov regularization, or ridge regression, is a popular technique to deal with collinearity in multivariate regression. We unveil a formal analogy between ridge regression and statistical mechanics, where the objective function is comparable to a free energy, and the ridge parameter plays the role of temperature. This analogy suggests two novel criteria for selecting a suitable ridge parameter: specific-heat (C_v) and maximum penalty (MP). We apply these fits to evaluate the relative contributions of rigid-body and internal fluctuations, which are typically highly collinear, to crystallographic B-factors. This issue is particularly important for computational models of protein dynamics, such as the elastic network model (ENM), since the amplitude of the predicted internal motion is commonly calibrated using B-factor data. After validation on simulated datasets, our results indicate that rigid-body motions account on average for more than 80% of the amplitude of B-factors. Furthermore, we evaluate the ability of different fits to reproduce the amplitudes of internal fluctuations in X-ray ensembles from the B-factors in the corresponding single X-ray structures. The new ridge criteria are shown to be markedly superior to the commonly used two-parameter fit that neglects rigid-body rotations and to the full fits regularized under generalized cross-validation. In conclusion, the proposed fits ensure a more robust calibration of the ENM force constant and should prove valuable in other applications.