Revisiting the (E + A) ⊗ (e + a) problems of polyatomic systems with trigonal symmetry: general expansions of their vibronic Hamiltonians†
Abstract
In this work, we derive general expansions in vibrational coordinates for the (E + A) ⊗ (e + a) vibronic Hamiltonians of molecules with one and only one C3 axis. We first derive the expansion for the lowest C3 symmetry. Additional symmetry elements systematically eliminate terms in the expansion. We compare our expansions with the previous results for two cases, the 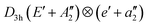 and the C3 (E + A) ⊗ e. The first comparison demonstrates the robustness, completeness, conciseness, and convenience of our formalism. There is a systematic discrepancy in the second comparison. We discuss the origin of the discrepancy and use a numerical example to corroborate our expansion. Our formalism covers 153 vibronic problems in 6 point groups. It also gives general expansions for the spin–orbit vibronic Hamiltonians of the p-type (E + A) ⊗ (e + a) problems.
and the C3 (E + A) ⊗ e. The first comparison demonstrates the robustness, completeness, conciseness, and convenience of our formalism. There is a systematic discrepancy in the second comparison. We discuss the origin of the discrepancy and use a numerical example to corroborate our expansion. Our formalism covers 153 vibronic problems in 6 point groups. It also gives general expansions for the spin–orbit vibronic Hamiltonians of the p-type (E + A) ⊗ (e + a) problems.
- This article is part of the themed collection: 2017 PCCP HOT Articles

 Please wait while we load your content...
Please wait while we load your content...