The defect level and ideal thermal conductivity of graphene uncovered by residual thermal reffusivity at the 0 K limit

Abstract

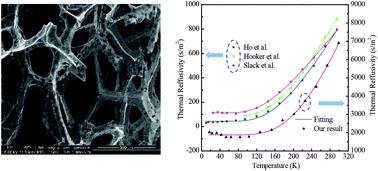
Due to its intriguing thermal and electrical properties, graphene has been widely studied for potential applications in sensor and energy devices. However, the reported value for its thermal conductivity spans from dozens to thousands of W m⁻¹ K⁻¹ due to different levels of alternations and defects in graphene samples. In this work, the thermal diffusivity of suspended four-layered graphene foam (GF) is characterized from room temperature (RT) down to 17 K. For the first time, we identify the defect level in graphene by evaluating the inverse of thermal diffusivity (termed “thermal reffusivity”: Θ) at the 0 K limit. By using the Debye model of Θ = Θ₀ + C × e^−θ/2T and fitting the Θ–T curve to the point of T = 0 K, we identify the defect level (Θ₀) and determine the Debye temperature of graphene. Θ₀ is found to be 1878 s m⁻² for the studied GF and 43–112 s m⁻² for three highly crystalline graphite materials. This uncovers a 16–43-fold higher defect level in GF than that in pyrolytic graphite. In GF, the phonon mean free path solely induced by defects and boundary scattering is determined as 166 nm. The Debye temperature of graphene is determined to be 1813 K, which is very close to the average theoretical Debye temperature (1911 K) of the three acoustic phonon modes in graphene. By subtracting the defect effect, we report the ideal thermal diffusivity and conductivity (κ_ideal) of graphene presented in the 3D foam structure in the range of 33–299 K. Detailed physics based on chemical composition and structure analysis are given to explain the κ_ideal–T profile by comparing with those reported for suspended graphene.