Geometric capture and escape of a microswimmer colliding with an obstacle
Abstract
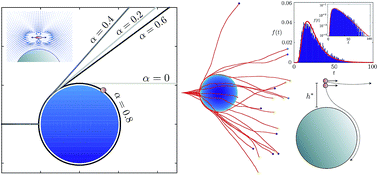
Motivated by recent experiments, we consider the hydrodynamic capture of a microswimmer near a stationary spherical obstacle. Simulations of model equations show that a swimmer approaching a small spherical colloid is simply scattered. In contrast, when the colloid is larger than a critical size it acts as a passive trap: the swimmer is hydrodynamically captured along closed trajectories and endlessly orbits around the colloidal sphere. In order to gain physical insight into this hydrodynamic scattering problem, we address it analytically. We provide expressions for the critical trapping radius, the depth of the “basin of attraction,” and the scattering angle, which show excellent agreement with our numerical findings. We also demonstrate and rationalize the strong impact of swimming-flow symmetries on the trapping efficiency. Finally, we give the swimmer an opportunity to escape the colloidal traps by considering the effects of Brownian, or active, diffusion. We show that in some cases the trapping time is governed by an Ornstein–Uhlenbeck process, which results in a trapping time distribution that is well-approximated as inverse-Gaussian. The predictions again compare very favorably with the numerical simulations. We envision applications of the theory to bioremediation, microorganism sorting techniques, and the study of bacterial populations in heterogeneous or porous environments.

 Please wait while we load your content...
Please wait while we load your content...