Graphene mechanics: I. Efficient first principles based Morse potential

Abstract

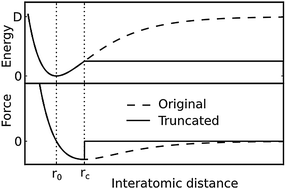
We present a computationally efficient pairwise potential for use in molecular dynamics simulations of large graphene or carbon nanotube systems, in particular, for those under mechanical deformation, and also for mixed systems including biomolecules. Based on the Morse potential, it is only slightly more complex and computationally expensive than a harmonic bond potential, allowing such large or mixed simulations to reach experimentally relevant time scales. By fitting to data obtained from quantum mechanics (QM) calculations to represent bond breaking in graphene patches, we obtain a dissociation energy of 805 kJ mol⁻¹ which reflects the steepness of the QM potential up to the inflection point. A distinctive feature of our potential is its truncation at the inflection point, allowing a realistic treatment of ruptured C–C bonds without relying on a bond order model. The results obtained from equilibrium MD simulations using our potential compare favorably with results obtained from experiments and from similar simulations with more complex and computationally expensive potentials.