Migration of a sphere in a viscoelastic fluid under planar shear flow: Experiments and numerical predictions

Abstract

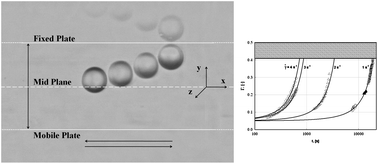
Solid–liquid disperse systems are complex fluids, extensively used for a variety of applications. The flow behavior of such materials is strongly dependent on the matrix rheological properties: when the suspending fluid shows viscoelastic behavior, isolated suspended particles in confined flow fields tend to migrate across the streamlines. In this work, we carry out a detailed experimental investigation of such migration phenomenon for a rigid, spherical particle in planar shear flow, and compare the experimental findings with 3D numerical simulations based on finite elements. A highly elastic non-Newtonian fluid is chosen as the suspending medium. The migration is studied by varying the confinement, the external shear rate and the fluid normal stresses. The particle is always found to move towards the closest wall, regardless of its initial position. For a fixed set of geometrical and flow parameters, the trajectories from different initial positions can be shifted in time to overlap on a single curve. Migration dynamics is governed by an exponential law as the particle is in the region around the midgap. Stronger confinements, higher shear rates and higher levels of normal stresses all enhance the migration speed. We found qualitative agreement between predictions from numerical simulations and experimental results.