Equations of explicitly-correlated coupled-cluster methods

Abstract

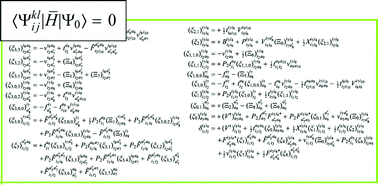
The tensor contraction expressions defining a variety of high-rank coupled-cluster energies and wave functions that include the interelectronic distances (r₁₂) explicitly (CC-R12) have been derived with the aid of a newly-developed computerized symbolic algebra SMITH. Efficient computational sequences to perform these tensor contractions have also been suggested, defining intermediate tensors—some reusable—as a sum of binary tensor contractions. SMITH can elucidate the index permutation symmetry of intermediate tensors that arise from a Slater-determinant expectation value of any number of excitation, deexcitation and other general second-quantized operators. SMITH also automates additional algebraic transformation steps specific to R12 methods, i.e. the identification and isolation of the special intermediates that need to be evaluated analytically and the resolution-of-the-identity insertion to facilitate high-dimensional molecular integral computation. The tensor contraction expressions defining the CC-R12 methods including through the connected quadruple excitation operator (CCSDTQ-R12) have been documented and efficient computational sequences have been suggested not just for the ground state but also for excited states via the equation-of-motion formalism (EOM-CC-R12) and for the so-called Λ equation (Λ-CC-R12) of the CC analytical gradient theory. Additional equations (the geminal amplitude equation) arise in CC-R12 that need to be solved to determine the coefficients multiplying the r₁₂-dependent factors. The operation cost of solving the geminal amplitude equations of rank-k CC-R12 and EOM-CC-R12 (right-hand side) scales as O(n⁶) (k = 2) or O(n⁷) (k ≥ 3) with the number of orbitals n and is surpassed by the cost of solving the usual amplitude equations O(n^2k+2). While the complexity of the geminal amplitude equations of Λ- and EOM-CC-R12 (left-hand side) nominally scales as O(n^2k+2), it is less than that of the other O(n^2k+2) terms in the usual amplitude equations. This suggests that the unabridged equations should be solved in high-rank CC-R12 for benchmark accuracy.