 Open Access Article
Open Access ArticleQuantum algorithm for alchemical optimization in material design†
Panagiotis Kl.
Barkoutsos
a,
Fotios
Gkritsis
ab,
Pauline J.
Ollitrault
ac,
Igor O.
Sokolov
 ad,
Stefan
Woerner
a and
Ivano
Tavernelli
ad,
Stefan
Woerner
a and
Ivano
Tavernelli
 *a
*a
aIBM Quantum, IBM Research – Zurich, 8803 Rüschlikon, Switzerland. E-mail: ita@zurich.ibm.com
bKing's College London, London, UK
cLaboratory of Physical Chemistry, ETH Zürich, 8093 Zürich, Switzerland
dDepartment of Chemistry, University of Zürich, Switzerland
First published on 22nd January 2021
Abstract
The development of tailored materials for specific applications is an active field of research in chemistry, material science and drug discovery. The number of possible molecules obtainable from a set of atomic species grow exponentially with the size of the system, limiting the efficiency of classical sampling algorithms. On the other hand, quantum computers can provide an efficient solution to the sampling of the chemical compound space for the optimization of a given molecular property. In this work, we propose a quantum algorithm for addressing the material design problem with a favourable scaling. The core of this approach is the representation of the space of candidate structures as a linear superposition of all possible atomic compositions. The corresponding ‘alchemical’ Hamiltonian drives the optimization in both the atomic and electronic spaces leading to the selection of the best fitting molecule, which optimizes a given property of the system, e.g., the interaction with an external potential as in drug design. The quantum advantage resides in the efficient calculation of the electronic structure properties together with the sampling of the exponentially large chemical compound space. We demonstrate both in simulations and with IBM Quantum hardware the efficiency of our scheme and highlight the results in a few test cases. This preliminary study can serve as a basis for the development of further material design quantum algorithms for near-term quantum computers.
1 Introduction
The chemical compound space (CCS), that is, the ensemble of possible molecules that can be constructed with a given set of atoms, is known to grow exponentially with the size of the molecular systems of interest. For example, in a 2004 Nature Insight issue the number of small organic molecules expected to be stable has been estimated to exceed 1060.1–3 By contrast, current records held by the Chemical Abstract Services of the American Chemical Society account for only 100 million compounds characterized so far.The vastness of the CCS offers a formidable opportunity for the discovery of new materials, but at the same time, it poses enormous challenges. In fact, while the exponentially large set of possible chemical species enables the potential design of novel molecules and materials with improved properties for numerous applications in physics, chemistry and biology, current experimental and computational techniques are still unable to perform an efficient optimization in such a high-dimensional space.
Classical approaches to molecular design are currently based either on deterministic algorithms to exploit function–structure relationships using first-principle (or force-fields based) solutions of the underlying physical models (e.g., Schrödinger's or Newton's equations of motion) or on machine learning (ML) and regression models, like the quantitative structure–activity relationship (QSAR) techniques.4 Rational design based on the quantum mechanical framework is crucial for the unbiased exploration of CCS since it enables, at least in principle, the exact and deterministic evaluation of system properties through the calculation of expectation values. However, the computational cost associated to this approach hampers a systematic exploration of the complete CCS, limiting drastically its applicability. On the other hand, despite a long tradition of ML methods in pharmaceutical applications5–9 and many successful applications as filters applied to large molecular libraries,10 the overall usefulness of ML for molecular design is still controversial.11,12 Of different nature are the alchemical perturbative approaches13–15 and the more recent ML techniques trained across the CCS and used to predict, among others, reorganization energies,16 chemical reactivity,17 and crystal properties.18,19 The automatic generation of ML models for classical and quantum observables has only recently been accomplished within the rigorous realm of physical chemistry.20 However, even though promising, these methods are still in their infancy and therefore not yet of general applicability.20
In the case of drug discovery, the main goal is often to find the ‘best’ molecular structure that is capable to produce favourable interaction with a given biological target like, for instance, the binding pocket of an enzyme. Also in this case, the number of accessible stable molecules that can potentially lead to a favourable drug–target interaction is immense. In the case of the optimization of the ligands associated to a known molecular motif (a molecular scaffold), the number of possible configurations obtained by associating a given ligand – selected from a ligand species database with ns elements – to each of the np insertion points of a given molecular scaffold grows exponentially as nsnp.
In this work, we introduce a quantum algorithm that enables the efficient simultaneous optimization of the atomic composition and corresponding electronic structure for an exponentially large set of molecules loaded as a linear superposition of structures in the Hilbert space of a N-qubit quantum register. Within this linear combination of all possible drug candidates the quantum optimization algorithm will then select a small subset of stable candidates with a favourable interaction with the external potential. The quantum advantage of this approach is therefore twofold. On one side, we benefit from the favorable 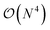 scaling for the solution of the Schrödinger equation (SE) in a quantum computer,21,22 and – on the other side – we can exploit the size of the qubit Hilbert space to efficiently scan the properties of an exponential set of potential drugs.
scaling for the solution of the Schrödinger equation (SE) in a quantum computer,21,22 and – on the other side – we can exploit the size of the qubit Hilbert space to efficiently scan the properties of an exponential set of potential drugs.
In this perspective, our quantum algorithm falls in the category of ‘inverse design’,23 namely the optimization of molecular structures given a desired target property. As such, this approach is not limited to the design of new drugs that minimize a given ligand–receptor interaction, but it can be easily generalized to the optimization of different properties of interest in chemistry and physics like, for instance, the optical absorption and emission of chromophores, the efficiency of new catalysts, and the prediction of binary alloys. This work is focusing exclusively on those aspects of the design process that determine the exponential cost of simulations and that can be addressed using a quantum computing algorithm. Additional steps including the molecular relaxation of the system and of its environment can be added without altering the scaling properties.
2 The alchemical Hamiltonian
In this work, we construct an ‘alchemical’ Hamiltonian that describes a linear superposition of all possible molecular structures generated by the insertion of ni molecular fragments chosen from a set with nl elements into a molecular scaffold of a defined structure. As an example, one can think about a simple drug scaffold such a cholesterol derivative and the attempt to improve its interaction with a target molecule by changing a subset of its functional groups. Even though our quantum algorithm can be generalized to any type of ligands, this study is limited to the single atomic ‘mutations’ of a given drug motif. The chemical nature of the atomic species is encoded in the nuclear charge and effective core potentials24 (ECP) that describe the effect of the atomic core electrons that are not treated explicitly in the solution of the corresponding electronic structure equation. The corresponding ‘alchemical’ Hamiltonian has the form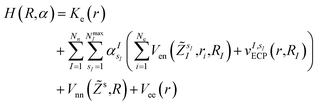 | (1) |
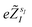 are the valence charges with
are the valence charges with 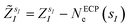 (where
(where 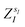 is the atomic number of atom I of species sI, e is the electron charge, NECPe(sI) are the number of electrons of the core), e
is the atomic number of atom I of species sI, e is the electron charge, NECPe(sI) are the number of electrons of the core), e![[Z with combining tilde]](https://www.rsc.org/images/entities/i_char_005a_0303.gif) s is the collective vector of all valence charges and all possible atomic species, I and i are indices for the atoms and the electrons, respectively, sI runs over the different chemical species associated to the atomic position I, NsI (with NmaxI = maxI{NsI}), and αIs are the ‘alchemical’ weights subject to the constraint
s is the collective vector of all valence charges and all possible atomic species, I and i are indices for the atoms and the electrons, respectively, sI runs over the different chemical species associated to the atomic position I, NsI (with NmaxI = maxI{NsI}), and αIs are the ‘alchemical’ weights subject to the constraint 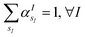 and α is the collective vector of all αIs. In eqn (1), Ke is the kinetic energy of the electrons, Vnn is the nuclear–nuclear interaction,
and α is the collective vector of all αIs. In eqn (1), Ke is the kinetic energy of the electrons, Vnn is the nuclear–nuclear interaction, 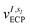 is the potential generated by the core electrons of atoms I in its ‘alchemical’ form sI, and finally Vee is the electron–electron interaction. All calculations are performed in the unrestricted formalism, without fixing the total electronic spin state. A detailed description of the different terms in given in the ESI.† The cost function that is used to score the different potential molecular candidates is given by the binding energy in the field generated by a set of external charges, qk placed in positions
is the potential generated by the core electrons of atoms I in its ‘alchemical’ form sI, and finally Vee is the electron–electron interaction. All calculations are performed in the unrestricted formalism, without fixing the total electronic spin state. A detailed description of the different terms in given in the ESI.† The cost function that is used to score the different potential molecular candidates is given by the binding energy in the field generated by a set of external charges, qk placed in positions ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) k and defined by
k and defined byΔE(R,α,![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) ,q) = EC(R,α, ,q) = EC(R,α,![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) ,q) − E(R,α) ,q) − E(R,α) | (2) |
![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) ,q) is the expectation value (ground state energy) of the system in the field of the external charges governed by the Hamiltonian
,q) is the expectation value (ground state energy) of the system in the field of the external charges governed by the Hamiltonian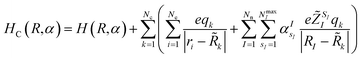 | (3) |
![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) ,q). The last two energy contributions are referred as Veq and Vnq, respectively. Note that in eqn (2) additional repulsion terms can be added to the cost function to account for eventual contacts between the system and its environment. Furthermore, structural relaxation can be added to the optimization procedure to prevent steric contacts between the two subsystems. Finally, in order to ensure stable molecular candidates with negative formation energies and reasonable electronic structure configurations, we can either add a new term to the cost function (eqn (2)) proportional to the system energy
,q). The last two energy contributions are referred as Veq and Vnq, respectively. Note that in eqn (2) additional repulsion terms can be added to the cost function to account for eventual contacts between the system and its environment. Furthermore, structural relaxation can be added to the optimization procedure to prevent steric contacts between the two subsystems. Finally, in order to ensure stable molecular candidates with negative formation energies and reasonable electronic structure configurations, we can either add a new term to the cost function (eqn (2)) proportional to the system energy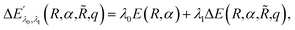 | (4) |
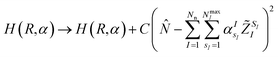 | (5) |
![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) is the electronic number operator and λ0, λ1 and C are tunable parameters. However, in none of the examples presented in this work it became necessary to introduce a penalty term of this kind.NIs
is the electronic number operator and λ0, λ1 and C are tunable parameters. However, in none of the examples presented in this work it became necessary to introduce a penalty term of this kind.NIs
The quantum algorithm requires the transformation of the ‘alchemical’ Hamiltonian in the second quantization framework.25–31 This needs the selection of one-electron basis functions, which is commonly assumed to be the set of molecular Hartree–Fock (HF) orbitals. However, this would imply the solution of the HF equations for each of the exponentially many possible structures obtained by assigning different atomic species (characterized by the ‘valence’ atomic number 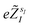 with sI in the set of considered elements) at each atomic position of the molecular scaffold. To avoid this potential pitfall, we prepare the second quantized Hamiltonian in the basis of the atomic functions, that in our case is given by the Gaussian STO-3G basis set.32,33 However, due to the non-orthogonality of the AO basis functions, a transformation into the orthonormal Löwdin's basis is required. Details are given in Section 6. We denote the elements of this basis set with ψp(r) where p is a collective index that runs over all basis functions associated to all atomic species allowed at each atomic position. The total number of such basis functions is therefore Ntb = NnNsNb, when we assume for simplicity that at each atomic position we have the same number of possible alternative atomic species (Ns), each one described by the same number of atomic basis functions
with sI in the set of considered elements) at each atomic position of the molecular scaffold. To avoid this potential pitfall, we prepare the second quantized Hamiltonian in the basis of the atomic functions, that in our case is given by the Gaussian STO-3G basis set.32,33 However, due to the non-orthogonality of the AO basis functions, a transformation into the orthonormal Löwdin's basis is required. Details are given in Section 6. We denote the elements of this basis set with ψp(r) where p is a collective index that runs over all basis functions associated to all atomic species allowed at each atomic position. The total number of such basis functions is therefore Ntb = NnNsNb, when we assume for simplicity that at each atomic position we have the same number of possible alternative atomic species (Ns), each one described by the same number of atomic basis functions 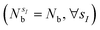 . The main drawback of this choice consists in the requirement of a larger number of qubits, N, for the construction of the molecular wavefunction, without, however, modifying the overall scaling of the algorithm, which remains
. The main drawback of this choice consists in the requirement of a larger number of qubits, N, for the construction of the molecular wavefunction, without, however, modifying the overall scaling of the algorithm, which remains 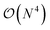 . The Hamiltonian in eqn (3) becomes
. The Hamiltonian in eqn (3) becomes
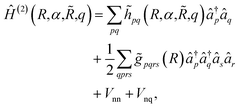 | (6) |
![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) pq(R,α,
pq(R,α,![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) ,q) are the sum of the matrix elements of the one-electron terms in eqn (1) and (3) (i.e., the potentials Ven,
,q) are the sum of the matrix elements of the one-electron terms in eqn (1) and (3) (i.e., the potentials Ven, 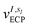 and Veq), and
and Veq), and ![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) pqrs are the two-electron integrals of the potential Vee, which depend only implicitly on R, α,
pqrs are the two-electron integrals of the potential Vee, which depend only implicitly on R, α, ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) , and q (see also Section 6 and the ESI†).
, and q (see also Section 6 and the ESI†).
Note that the ‘alchemical’ Hamiltonian (eqn (3)) has the same complexity as the original electronic structure problem formulated in second quantization, with the only difference that the ground state solution is now evaluated for a superposition of structures characterized by the coefficients 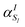 . Thanks to the quantization in the atomic basis, we achieve to break down the exponential cost to linear, since each atom in the molecule is contributing to the total wavefunction with a set of independent orbitals of the size NIs.
. Thanks to the quantization in the atomic basis, we achieve to break down the exponential cost to linear, since each atom in the molecule is contributing to the total wavefunction with a set of independent orbitals of the size NIs.
The optimization of the ‘alchemical’ system wavefunctions Ψ(r;R) and Ψ′(r;R,α,![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) ,q), respectively in the absence and in the presence of the external potential generated by the point charges, is performed using the variational quantum eigensolver (VQE) algorithm.34 For an initial set of parameters α, the circuit in Fig. 2(a) evaluates a trial wavefunction for the corresponding linear superposition of molecular Hamiltonians. The wavefunction is parametrized by the single qubit rotation angles, θ = {θ1, …, θM} (where M is the total number of parametrized gates) according to the hardware-efficient Ansatz described in ref. 26 and 27. In the most general case, the total number of the electrons is not fixed during the optimization, but it varies as the atomic composition of the ensemble evolves, in such a way to minimize the molecular potential energy and maximize the interaction with the environment. This is achieved with the use of the so-called hardware efficient wavefunction Ansätze27 that, while providing an efficient way of generating entangled trial states, enable the sampling of the full electronic Fock space without imposing any constraint on the total number of electrons. However, when needed, it is also possible to confine the search within the subspace corresponding to the desired number of electrons or to a given molecular total charge by means of a constraint such as the one given in eqn (5). At each VQE iteration both parameter sets, {θ, α}, are updated in order to minimize the cost function ΔE(R,α,
,q), respectively in the absence and in the presence of the external potential generated by the point charges, is performed using the variational quantum eigensolver (VQE) algorithm.34 For an initial set of parameters α, the circuit in Fig. 2(a) evaluates a trial wavefunction for the corresponding linear superposition of molecular Hamiltonians. The wavefunction is parametrized by the single qubit rotation angles, θ = {θ1, …, θM} (where M is the total number of parametrized gates) according to the hardware-efficient Ansatz described in ref. 26 and 27. In the most general case, the total number of the electrons is not fixed during the optimization, but it varies as the atomic composition of the ensemble evolves, in such a way to minimize the molecular potential energy and maximize the interaction with the environment. This is achieved with the use of the so-called hardware efficient wavefunction Ansätze27 that, while providing an efficient way of generating entangled trial states, enable the sampling of the full electronic Fock space without imposing any constraint on the total number of electrons. However, when needed, it is also possible to confine the search within the subspace corresponding to the desired number of electrons or to a given molecular total charge by means of a constraint such as the one given in eqn (5). At each VQE iteration both parameter sets, {θ, α}, are updated in order to minimize the cost function ΔE(R,α,![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) ,q) in eqn (2) for fixed values of the charges and corresponding positions (
,q) in eqn (2) for fixed values of the charges and corresponding positions (![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) , q). Note that in this application we are dealing with a modified version of the original VQE algorithm in which the optimization is extended to a set of parameters α that defines the cost function. At convergence, the algorithm provides the set of optimized parameters {θopt, αopt}, which defines the ‘alchemical’ state that minimizes the interaction with the environment. This corresponds to a superposition of possible physical states (molecules) weighted by the coefficients αopt. The final step consists in the selection of the most suited atomic species to be located at the atomic site I of the optimized molecule, according to the sampled VQE distributions (see the Results section). The algorithm can converge towards a pool of potential candidates with similar scoring values instead of a single structure. In this case, after imposing a threshold value, it is possible to identify a small subset of molecules that can be further analyzed.
, q). Note that in this application we are dealing with a modified version of the original VQE algorithm in which the optimization is extended to a set of parameters α that defines the cost function. At convergence, the algorithm provides the set of optimized parameters {θopt, αopt}, which defines the ‘alchemical’ state that minimizes the interaction with the environment. This corresponds to a superposition of possible physical states (molecules) weighted by the coefficients αopt. The final step consists in the selection of the most suited atomic species to be located at the atomic site I of the optimized molecule, according to the sampled VQE distributions (see the Results section). The algorithm can converge towards a pool of potential candidates with similar scoring values instead of a single structure. In this case, after imposing a threshold value, it is possible to identify a small subset of molecules that can be further analyzed.
3 Models and simulations
As a proof-of-principle example, we consider the case of a diatomic molecule placed at the center of the six charges disposed in a bipyramidal arrangement as shown in Fig. 1(a). The atomic species at each molecular site can be selected from a set composed by the light elements S = {H, Li, Na} of the first column of the periodic table, which are characterized by a single valence electron. The number of possible molecules generated is therefore nsnp = 32, since due to the potential asymmetry of the axial charges the XY molecule may have a different binding energy than the reversed YX molecule, with X, Y ∈ S. This choice allows us to keep the number of qubits and the circuit depth of the VQE implementation within the limits of what can be afforded using state-of-the-art simulators and quantum hardware, without limiting the generality of the approach. The equatorial charges (as shown in Fig. 1(a) in blue) are all set to the same value, while the axial charges (as shown in Fig. 1(a) in orange) are varied in order to favour different target molecules. The different charge setups are summarized in the table of Fig. 1(e).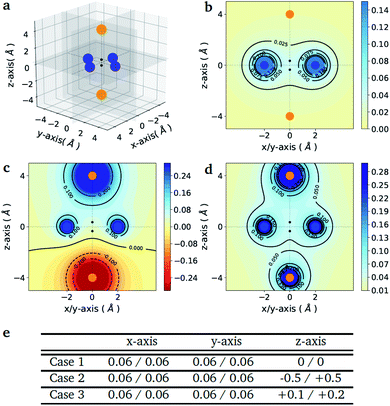 | ||
| Fig. 1 Point charge distributions. (a) Position of the point charges (blue and orange dots) relative to the molecule to optimize (black dots). Shown is the case of the H2 molecule. The orange charges along z-axis are allowed to change (values reported in panel (e)) whereas the blue charges are kept fixed at the value of 0.06. (b–d) Contour plots of the potential energy generated by the 6 point charges in the xz plane for the three different cases given in the table below (panel e). The potentials are in atomic units. (e) Value of the charges (in the unit of the fundamental electronic charge e) used to generate the 3 different external potentials. For all molecules (A1–A2) in Fig. 2 (panel e) the first atom (A1) is the one with negative z-coordinate. | ||
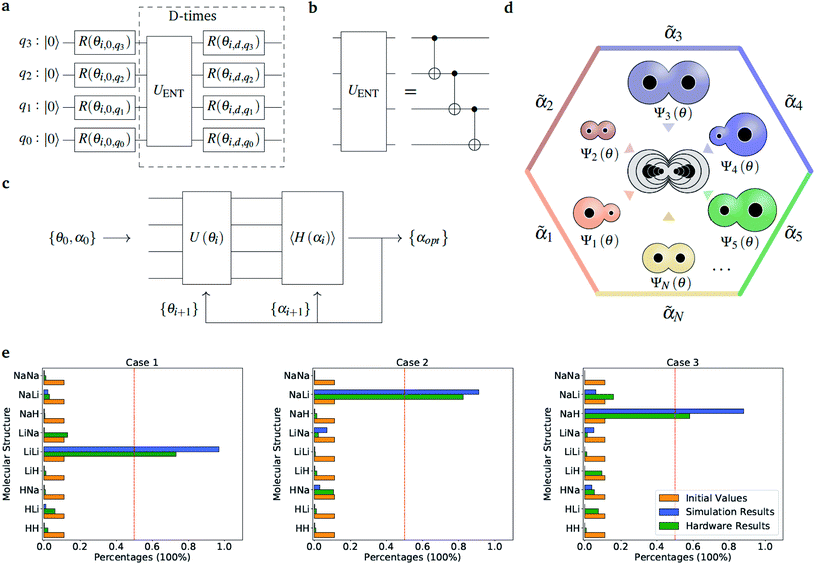 | ||
Fig. 2 Diatomic molecules in a point charge environment. (a) Variational circuit used to generate the trial alchemical wavefunctions (for this case D = 2). (b) Entanglement block used in the variational form for the hardware runs. In the classical simulations, we used entangler blocks connecting all qubits. (c) Circuit and feedback loop used to update the wavefunction parameters (circuit variables) and the alchemical weights (of the Hamiltonian). (d) Sketch of the molecular superposition state with the contribution of 6 (over N) representative molecules participating to the ensemble, each contributing with the probability  . (e) Distribution of the molecular propensities for each of the three charge distributions described in Fig. 1(e). The initial uniform distribution is shown in orange. The converged VQE distributions obtained in simulations and hardware calculations are given in blue and green, respectively. . (e) Distribution of the molecular propensities for each of the three charge distributions described in Fig. 1(e). The initial uniform distribution is shown in orange. The converged VQE distributions obtained in simulations and hardware calculations are given in blue and green, respectively. | ||
For all three elements we used a STO-3G basis set, which amounts to 1, 5, 9 atomic basis functions for H, Li, and Na, respectively. In order to keep the number of qubits and the number of matrix elements hμν(R,α,![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) ,q) and gμνκλ(R) constant for all molecules, we extended the active space for every molecule according to the minimum active space requirements of the largest molecule (see also Section 6).
,q) and gμνκλ(R) constant for all molecules, we extended the active space for every molecule according to the minimum active space requirements of the largest molecule (see also Section 6).
The bond distances used to compute the matrix elements for the potentials 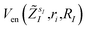 and
and 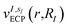 of eqn (1) (which also contribute to hμν(R,α,
of eqn (1) (which also contribute to hμν(R,α,![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) ,q)) are obtained from tabulated values, provided from ref. 35. In the case of more complex molecular scaffolds, the algorithm can be extended to include a geometry optimization step where atomic forces are computed from additional measurements of the gradients of the Hamiltonian performed using the ‘alchemical’ wavefunction Ψ(r;R,α,
,q)) are obtained from tabulated values, provided from ref. 35. In the case of more complex molecular scaffolds, the algorithm can be extended to include a geometry optimization step where atomic forces are computed from additional measurements of the gradients of the Hamiltonian performed using the ‘alchemical’ wavefunction Ψ(r;R,α,![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) ,q) at each VQE iteration.36,37 The cost of the geometry optimization step does not modify the scaling of the algorithm but only implies additional 6Nn measurements, all performed with the same VQE alchemical wavefunction.
,q) at each VQE iteration.36,37 The cost of the geometry optimization step does not modify the scaling of the algorithm but only implies additional 6Nn measurements, all performed with the same VQE alchemical wavefunction.
As a second application, we investigate the binding affinity for different diatomic gases in the binding pocket of the hemeprotein H-NOX (PDB entry code: 3TFA). This protein is involved in sensing and signaling the presence of simple gas molecules in the environment. In particular, in H-NOX one can identify a series of apolar channels that connect the exterior of the protein to the buried heme group. The nature of the hydrophobic pockets arranged along the channels favours the selectivity of the gas molecules and their mobility (see Fig. 3(b)). In this study, we compute in a single VQE simulation the binding affinity for all possible diatomic molecules that can be generated from the set {C, N, O, S} (the ones chemically unstable are naturally discarded due to their unfavourable formation energies). The center of mass of all molecules is placed at the position of the Xe atom that occupies the binding pocket in the X-ray structure.38 The optimal orientation of the diatomic molecules in the pocket is determined for a single element of the ensemble (namely the molecule CO) and kept fix during the VQE optimization. The binding energies obtained for all stable molecules are reported in Table VI of the ESI.†
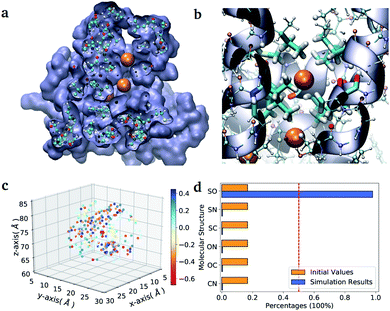 | ||
| Fig. 3 Diatomic molecules in a protein environment. (a) X-ray crystal structure of the protein H-NOX (PBD entry code 3TFA) showing the main channel with three binding pockets occupied by Xe atoms (orange spheres). (b) Zoom into the first binding pocket with highlighted the apolar residues that favour the selection and diffusion of the gas molecules. The orange spheres indicate the position of the co-crystallized Xe atoms, which mark the center of the binding pockets. (c) Position of the point charges used to mimic the enzyme pocket. The red dot corresponds to the center of the diatomic molecules. (d) Initial and final distributions of the molecular structures obtained with the ‘alchemical’ optimization. | ||
4 Results and discussion
Fig. 1(e) reports the 3 charge distributions used to test the proposed method. For each of these charge sets, we optimized the atomic species of the diatomic molecule placed at the center of the charge distribution (see Fig. 1) sampling the elements from the set {H, Li, Na}. Two-dimensional cuts of the electrostatic potentials generated by the different charge arrangements are shown in Fig. 1(b)–(d). It is under the influence of these electrostatic potentials that the different atomic compositions for the dimer are selected.The VQE is initialized using an unbiased distribution of the atomic weights associated to each atomic position, namely 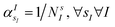 so that
so that 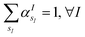 . All Ntb qubits are initialized in state ‘1’ (note that the choice of atomic basis functions in place of molecular (HF) ones implies the possible occupation of all orbitals in the generation of the system wavefunction). As a consequence, the circuit used to sample the ‘alchemical’ wavefunction is not required to conserve the total occupation number (i.e., the number of ‘1’ in the qubit register). Fig. 2(e) shows the evolution of the atomic compositions at the two molecular sites of the system in Fig. 2(a) throughout the optimization process for different choices of the external charges (see table in Fig. 1(e)). Starting from the initial equally distributed atomic compositions we observe in all cases a smooth increase of the population of a given atomic species at each of the two atomic positions. As expected, the most probable final structure depends on the choice of the external potential. The correctness of our predictions are confirmed with an a posteriori calculation of the binding energies using an equivalent classical algorithm. The results of this comparison are reported in ESI, Table V.† Note that in the case the algorithm converges in a broad distribution of candidates, L1-regularization techniques can be used to enhance the sampling towards a restricted set of structures (see also ESI†).
. All Ntb qubits are initialized in state ‘1’ (note that the choice of atomic basis functions in place of molecular (HF) ones implies the possible occupation of all orbitals in the generation of the system wavefunction). As a consequence, the circuit used to sample the ‘alchemical’ wavefunction is not required to conserve the total occupation number (i.e., the number of ‘1’ in the qubit register). Fig. 2(e) shows the evolution of the atomic compositions at the two molecular sites of the system in Fig. 2(a) throughout the optimization process for different choices of the external charges (see table in Fig. 1(e)). Starting from the initial equally distributed atomic compositions we observe in all cases a smooth increase of the population of a given atomic species at each of the two atomic positions. As expected, the most probable final structure depends on the choice of the external potential. The correctness of our predictions are confirmed with an a posteriori calculation of the binding energies using an equivalent classical algorithm. The results of this comparison are reported in ESI, Table V.† Note that in the case the algorithm converges in a broad distribution of candidates, L1-regularization techniques can be used to enhance the sampling towards a restricted set of structures (see also ESI†).
In the case of H-NOX simulation, we determined the diatomic molecule obtained combining two elements from the set {C, O, N, S}, which has the best affinity for the first binding pocket exposed to the solvent. The simulation of the ‘alchemical’ quantum algorithm proposed in this work unequivocally selects the molecule SO, independently from the orientation of the molecular axis (see ESI† for the details on the calculation). The solution is in agreement with the ‘classical’ solution obtained by scanning the binding energy of all possible molecules.
5 Conclusions
In this work, we present a method for the design of molecular systems that best fit in a given external potential using an ‘alchemical’ quantum algorithm that simultaneously optimizes the electronic structure and the nuclear composition of given compounds. The search occurs in the exponentially large chemical compound space, which hampers an efficient implementation using classical algorithms, also due to the cost associated to the solution of the SE. The advantage of our approach is two-fold: it leverages the favourable scaling of quantum electronic structure algorithms (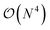 in the number of basis functions) as well as the possibility to search in an exponentially large space using a polynomial number of resources (i.e., number of qubits and gate operations).
in the number of basis functions) as well as the possibility to search in an exponentially large space using a polynomial number of resources (i.e., number of qubits and gate operations).
The algorithm was successfully applied to the optimization of a diatomic molecule composed by elements from the ensemble {H, Li, Na} placed in an external potential generated by 6 point charges. Simulations and hardware calculations performed on ibmq_singapore chip could unequivocally identify the best fitting molecule over an ensemble of 9 possible structures. To further validate our approach, we also apply the same algorithm for the determination of the diatomic molecules (with elements from the ensemble C, O, N and S) that best fit in the binding pocket of the hemeprotein H-NOX represented by 330 point charges. Also in this case, the simulation correctly selects the most stable molecule, namely SO, as confirmed by electronic structure and DFT calculations shown in ESI (Table VI).†
In conclusion, we propose and demonstrate a quantum algorithm which enables the optimization of chemical structures in a given external potential. The results illustrate the potential of quantum algorithms as a tool for the efficient and accurate sampling of the chemical compound space and open up new perspectives for the use of quantum computers in material design and drug discovery applications.
6 Computational methods
In order to ensure that the ‘alchemical’ Hamiltonian can be encoded in the same qubit register, we used the same number of basis functions for all molecules. This required the extension of the active space with ‘empty’ basis functions for the atomic species with less valence electrons. For instance, in the case of combinations made of atoms C, N, O, S the minimum active space required is composed by 8 atomic orbitals (16 qubits) as needed by the SN molecule.In this work, we used a localized basis set composed of atom centered orbitals 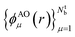 . The main consequences of this choice can be summarized as follows:
. The main consequences of this choice can be summarized as follows:
(i) Orbitals are not orthogonal to each other
| 〈ϕAOμ(r)|ϕAOν(r)〉 = Sμν ≠ δμν | (7) |
(ii) The commutation rules for the corresponding creation and annihilation operators: ĉ†μ,ĉμ become
| [ĉ†μ,ĉ†ν]+ = 0 | (8) |
| [ĉμ,ĉν]+ = 0 | (9) |
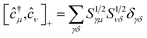 | (10) |
(iii) Löwdin rules for the calculation of matrix elements are modified as described for instance in ref. 39.
The Hamiltonian in the AO basis has the usual form
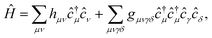 | (11) |
Points (ii) and (iii) can be demonstrated applying the Löwdin's orthogonalization procedure defined by the new set of orthogonal Löwdin's orbitals
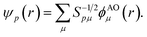 | (12) |
In order to circumvent the problem associated to the non-conventional commutation rules of eqn (10), we therefore rewrite the Hamiltonian of eqn (11) in the new orthonormal basis
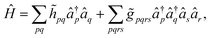 | (13) |
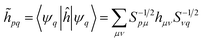 | (14) |
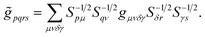 | (15) |
The operators â†i and âi defined as
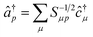 | (16) |
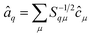 | (17) |
The simulation of the ‘alchemical’ Hamiltonian is executed in the Qiskit40 framework. For the classical optimization procedure, we employed the SLSQP optimizer as integrated in Qiskit Aqua. To ensure that the alchemical parameters remain within the interval [0,1], we implemented in the SLSQP algorithm a constraint of the form 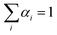 . The wavefunction parameters were initialized randomly within the interval [0, π]. After each optimization run, the parameters were re-initialized with the values estimated in the previous step. All qubit angles θ were constrained in the interval 0 to 2π. In the classical simulations of the quantum algorithm we set the maximum number of iterations to 500, while for the calculations on hardware we used 100 iterations.
. The wavefunction parameters were initialized randomly within the interval [0, π]. After each optimization run, the parameters were re-initialized with the values estimated in the previous step. All qubit angles θ were constrained in the interval 0 to 2π. In the classical simulations of the quantum algorithm we set the maximum number of iterations to 500, while for the calculations on hardware we used 100 iterations.
In the optimization process, we observed that multiplying the binding energies by a factor f allows for a faster convergence of the VQE. For this reason, the minimization was driven by the cost function minθ〈ψ(θ)|f(HC(R,α) − H(R,α))|ψ(θ)〉 while the binding energies were calculated using (〈ψ(θ)|f(HC(R,α) − H(R,α))|ψ(θ)〉)/f. For the results in Fig. 2 a factor f = 103 was used while for the system described in Fig. 3 we chose f = 104. To improve the convergence of the algorithm, we performed several restarts of the VQE algorithm using as initial parameters the ones outputted in the previous optimization loop.
The hardware runs were executed on ibmq_singapore 20-qubit chip via Qiskit.40 The connectivity of the chip is shown in ESI, Fig. 1.† In all runs, we used 8192 measurements and we exploited the natural connectivity of the qubits to implement the variational circuit (Fig. 2(a) and (b)).
Conflicts of interest
The authors declare no competing interests.Acknowledgements
P. J. O., I. O. S. and I. T. acknowledge financial support from the Swiss National Science Foundation (SNF) through the grant No. 200021-179312. All authors acknowledge support from Ismael Faro and interesting discussions with Alessandro Curioni and the whole IBM Quantum team. IBM, IBM Q, IBM Quantum, Qiskit are trademarks of International Business Machines Corporation, registered in many jurisdictions worldwide. Other product or service names may be trademarks or service marks of IBM or other companies.Notes and references
- P. Kirkpatrick and C. Ellis, Chemical space, Nature, 2004, 432(7019), 823 CrossRef CAS.
- C. Lipinski and A. Hopkins, Navigating chemical space for biology and medicine, Nature, 2004, 432(7019), 855–861 CrossRef CAS.
- C. M. Dobson, Chemical space and biology, Nature, 2004, 432(7019), 824–828 CrossRef CAS.
- K. Roy, S. Kar, and R. N. Das. A Primer on QSAR/QSPR Modeling: Fundamental Concepts. Springer International Publishing, 2015 Search PubMed.
- 3D QSAR in Drug Design, Volume 1: Theory Methods and Applications, ed. H. Kubinyi, Springer Netherlands, 1994 Search PubMed.
- J.-L. Faulon, D. P. Visco and R. S. Pophale, The signature molecular descriptor. 1. using extended valence sequences in qsar and qspr studies, J. Chem. Inf. Comput. Sci., 2003, 43(3), 707–720 CrossRef CAS.
- A. Golbraikh, M. Shen, Z. Xiao, Y.-D. Xiao, K.-H. Lee and T. Alexander, Rational selection of training and test sets for the development of validated qsar models, J. Comput.-Aided Mol. Des., 2003, 17(2), 241–253 CrossRef CAS.
- O. Ivanciuc, Qsar comparative study of wiener descriptors for weighted molecular graphs, J. Chem. Inf. Comput. Sci., 2000, 40(6), 1412–1422 CrossRef CAS.
- P. Baldi, K.-R. Müller and G. Schneider, Editorial: Charting chemical space: Challenges and opportunities for artificial intelligence and machine learning, Mol. Inf., 2011, 30(9), 751 CrossRef CAS.
- M. N. Drwal and R. Griffith, Combination of ligand- and structure-based methods in virtual screening, Drug Discovery Today: Technol., 2013, 10(3), e395–e401 CrossRef.
- A. F. Wagner, G. C. Schatz and J. M. Bowman, The evaluation of fitting functions for the representation of an O(3P)+H2 potential energy surface. I, J. Chem. Phys., 1981, 74(9), 4960–4983 CrossRef CAS.
- G. Schneider, Virtual screening: an endless staircase?, Nat. Rev. Drug Discovery, 2010, 9, 273–276 CrossRef CAS.
- K. Y. Samuel Chang, S. Fias, R. Ramakrishnan and O. Anatole von Lilienfeld, Fast and accurate predictions of covalent bonds in chemical space, J. Chem. Phys., 2016, 144(17), 174110 CrossRef.
- A. Solovyeva and O. Anatole von Lilienfeld, Alchemical screening of ionic crystals, Phys. Chem. Chem. Phys., 2016, 18, 31078–31091 RSC.
- K. Y. Samuel Chang and O. Anatole von Lilienfeld, AlxGa1−xAs crystals with direct 2 eV band gaps from computational alchemy, Phys. Rev. Mater., 2018, 2, 073802 CrossRef.
- M. Misra, D. Andrienko, B. Baumeier, J.-L. Faulon and O. Anatole von Lilienfeld, Toward quantitative structure–property relationships for charge transfer rates of polycyclic aromatic hydrocarbons, J. Chem. Theory Comput., 2011, 7(8), 2549–2555 CrossRef CAS.
- M. A. Kayala and P. Baldi, Reactionpredictor: Prediction of complex chemical reactions at the mechanistic level using machine learning, J. Chem. Inf. Model., 2012, 52(10), 2526–2540 CrossRef CAS.
- K. T. Schütt, H. Glawe, F. Brockherde, A. Sanna, K. R. Müller and E. K. U. Gross, How to represent crystal structures for machine learning: Towards fast prediction of electronic properties, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 205118 CrossRef.
- B. Meredig, A. Agrawal, S. Kirklin, J. E. Saal, J. W. Doak, A. Thompson, K. Zhang, A. Choudhary and C. Wolverton, Combinatorial screening for new materials in unconstrained composition space with machine learning, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 094104 CrossRef.
- M. Rupp, T. Alexandre, Klaus-Robert Müller and O. Anatole von Lilienfeld, Fast and accurate modeling of molecular atomization energies with machine learning, Phys. Rev. Lett., 2012, 108, 058301 CrossRef.
- Note that the number of measurements needed to achieve a given statistical accuracy ε2 of the total energy (where ε is defined as the standard error at the 68% confidence interval22) scales
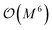 , where M is the number of basis functions used.
, where M is the number of basis functions used. - J. R. McClean, B. Ryan, P. J. Love and A. Aspuru-Guzik, Exploiting locality in quantum computation for quantum chemistry, J. Phys. Chem. Lett., 2014, 5(24), 4368–4380 CrossRef CAS.
- M. Wang, X. Hu, D. N. Beratan and W. Yang, Designing molecules by optimizing potentials, J. Am. Chem. Soc., 2006, 128(10), 3228–3232 CrossRef CAS.
- H. Hellmann, A new approximation method in the problem of many electrons, J. Chem. Phys., 1935, 3(1), 61 CrossRef.
- J. Romero, B. Ryan, J. R. McClean, C. Hempel, P. J. Love and A. Aspuru-Guzik, Strategies for quantum computing molecular energies using the unitary coupled cluster ansatz, Quantum Sci. Technol., 2018, 4(1), 014008 CrossRef.
- P. Kl Barkoutsos, J. F. Gonthier, I. Sokolov, N. Moll, G. Salis, A. Fuhrer, M. Ganzhorn, D. J. Egger, M. Troyer and A. Mezzacapo, et al., Quantum algorithms for electronic structure calculations: Particle-hole hamiltonian and optimized wave-function expansions, Phys. Rev. A, 2018, 98(2), 022322 CrossRef CAS.
- A. Kandala, A. Mezzacapo, K. Temme, M. Takita, M. Brink, J. M. Chow and J. M. Gambetta, Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets, Nature, 2017, 549(7671), 242–246 CrossRef CAS.
- P. J. J. O'Malley, et al., Scalable quantum simulation of molecular energies, Phys. Rev. X, 2017, 6, 031007 Search PubMed.
- I. Sokolov, P. K. Barkoutsos, P. J. Ollitrault, D. Greenberg, J. Rice, M. Pistoia and I. Tavernelli, Quantum orbital-optimized unitary coupled cluster methods in the strongly correlated regime: Can quantum algorithms outperform their classical equivalents?, J. Chem. Phys., 2020, 52, 124107 CrossRef.
- M. Reiher, W. Nathan, K. M. Svore, D. Wecker and M. Troyer, Elucidating reaction mechanisms on quantum computers, Proc. Natl. Acad. Sci. U. S. A., 2017, 29, 7555–7560 CrossRef.
- Y. Cao, J. Romero, J. P. Olson, M. Degroote, P. D. Johnson, M. Kieferová, I. D. Kivlichan, T. Menke, P. Borja and N. P. D. Sawaya, et al., Quantum chemistry in the age of quantum computing, Chem. Rev., 2019, 119(19), 10856–10915 CrossRef CAS.
- J. Frank, Atomic orbital basis sets, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3(3), 273–295 Search PubMed.
- W. J. Hehre, R. F. Stewart and J. A. Pople, Self-consistent molecular-orbital methods. i. use of gaussian expansions of slater-type atomic orbitals, J. Chem. Phys., 1969, 51(6), 2657–2664 CrossRef CAS.
- P. Alberto, J. McClean, P. Shadbolt, Y. Man-Hong, X.-Qi Zhou, P. J. Love, A. Aspuru-Guzik and J. L. O’Brien, A variational eigenvalue solver on a photonic quantum processor, Nat. Commun., 2014, 5, 1 Search PubMed.
- NIST Computational Chemistry Comparison and Benchmark Database; NIST Standard Reference Database Number 101, http://cccbdb.nist.gov/ Search PubMed.
- T. E. O'Brien, S. Bruno, R. Sagastizabal, X. Bonet-Monroig, A. Dutkiewicz, F. Buda, L. DiCarlo and L. Visscher, Calculating energy derivatives for quantum chemistry on a quantum computer, npj Quantum Inf., 2019, 5(1), 1–12 CrossRef.
- I. O. Sokolov, P. K. Barkoutsos, L. Moeller, P. Suchsland, G. Mazzola, and I. Tavernelli, Microcanonical and finite temperature ab initio molecular dynamics simulations on quantum computers, 2020, arXiv:2008.08144 [quant-ph].
- M. B. Winter, M. A. Herzik, J. Kuriyan and M. A. Marletta, Tunnels modulate ligand flux in a heme nitric oxide/oxygen binding (h-nox) domain, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(43), E881–E889 CrossRef CAS.
- P. R. Surján, Second Quantization for Nonorthogonal Orbitals, Springer Berlin Heidelberg, Berlin, Heidelberg, 1989, pp. 103–113 Search PubMed.
- G. Aleksandrowicz, T. Alexander, P. Barkoutsos, L. Bello, Y. Ben-Haim, D. Bucher, F. J. Cabrera-Hernández, J. Carballo-Franquis, A. Chen, C.-F. Chen, J. M. Chow, A. D. Córcoles-Gonzales, A. J. Cross, A. Cross, J. Cruz-Benito, C. Culver, S. D. L. P. González, E. De La Torre, D. Ding, E. Dumitrescu, I. Duran, P. Eendebak, M. Everitt, I. F. Sertage, A. Frisch, A. Fuhrer, J. Gambetta, B. G. Gago, J. Gomez-Mosquera, D. Greenberg, I. Hamamura, V. Havlicek, J. Hellmers, Ł. Herok, H. Horii, S. Hu, T. Imamichi, T. Itoko, A. Javadi-Abhari, N. Kanazawa, A. Karazeev, K. Krsulich, P. Liu, Y. Luh, Y. Maeng, M. Marques, F. J. Martín-Fernández, D. T. McClure, D. McKay, S. Meesala, A. Mezzacapo, N. Moll, D. M. Rodríguez, G. Nannicini, P. Nation, P. Ollitrault, L. J. O'Riordan, H. Paik, J. Pérez, A. Phan, M. Pistoia, V. Prutyanov, M. Reuter, J. Rice, A. R. Davila, R. H. P. Rudy, M. Ryu, N. Sathaye, C. Schnabel, E. Schoute, K. Setia, Y. Shi, A. Silva, Y. Siraichi, S. Sivarajah, J. A. Smolin, M. Soeken, H. Takahashi, I. Tavernelli, C. Taylor, P. Taylour, K. Trabing, M. Treinish, W. Turner, D. Vogt-Lee, C. Vuillot, J. A. Wildstrom, J. Wilson, E. Winston, C. Wood, S. Wood, S. Wörner, I. Y. Akhalwaya, and C. Zoufal, Qiskit: An open-source framework for quantum computing, 2019 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc05718e |
| This journal is © The Royal Society of Chemistry 2021 |
