Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Rational design of transparent p-type conducting non-oxide materials from high-throughput calculations†
Ramya
Kormath Madam Raghupathy
*a,
Thomas D.
Kühne
b,
Claudia
Felser
a and
Hossein
Mirhosseini
 *a
*a
aMax-Planck-Institute for Chemical Physics of Solids, D-01187 Dresden, Germany. E-mail: ramya@cpfs.mpg.de; hossein.mirhosseini@cpfs.mpg.de; Tel: +49 351 4646-3249
bDepartment of Chemistry, University of Paderborn, Warburger Str. 100, 33098 Paderborn, Germany
First published on 14th December 2017
Abstract
In this work, high-throughput ab initio calculations are employed to identify the most promising chalcogenide-based semiconductors for p-type transparent conducting materials (TCMs). A large computational data set is investigated by data mining. Binary semiconductors with large band gaps (Eg) and anions that are less electronegative than oxygen are considered. The roles of intrinsic defects and extrinsic dopants are investigated to probe the p-type performance of these semiconductors. Nine novel p-type non-oxide TCMs that have a low hole effective mass, good optical transparency, and hole dopability are proposed (ZnS, ZnSe, ZnTe, MgS, MgTe, GaSe, GaTe, Al2Se3, and BeTe). This study also focuses on a material engineering approach to modulate the electronic properties as a function of the layer thickness and external stress.
1 Introduction
Transparent conducting materials (TCMs) have been widely investigated owing to their diverse applications ranging from solar cells to transparent electronics.1–4 Potential materials for TCMs should offer two contradictory properties: a wide band gap and a low carrier effective mass.5 Among various TCMs, oxides have been widely studied owing to their stability, low electron effective mass, and optical transparency.6 Previous research on transparent conducting oxides (TCOs) has shown their outstanding properties as high-performance n-type conductors in transparent transistors, UV light-emitting diodes, detectors, gas sensors, and solar cells.7 However, in many optoelectronic applications, such as interlayer electrodes in tandem cells, high-performance p-type TCMs are required. The performance of p-type TCOs is hindered by the localized p states of oxygen in the valence band, which results in heavy holes.8,9 Demands for p-type TCMs and the deficient performance of this class of material have promoted intensive research efforts from academia and industry to rationalize and design potential p-type TCMs.4,10The discovery of CuAlO2 as a promising p-type TCO led to the development of rational design rules for p-type TCOs containing Cu1+ and prompted an extensive investigation of Cu-based materials.11 Experimental and theoretical efforts also revealed that mixing O with other anions, such as S and Se, influences p-type dopability. For example, p-type dopability has been observed in LaCuOS and BaCuOSe based compounds.12 Further, mixing of other anions with oxygen leads to higher valence band energies, making ternary oxides promising p-type conductors.8,13,14 In addition, p-type dopability has been tested for a series of compounds in which Cu is replaced by other cations (X2SeO2 (X = La, Pr, Gd, and Nd)).15 However, p-type TCOs are commonly hampered by the carrier mobility of candidate materials.16 Hence, there is a necessity for enhanced research efforts towards the rational design of suitable materials beyond TCOs.
Experimental studies and theoretical calculations have also been performed on non-oxide TCMs to determine the underlying physics of p-type TCMs. It has been shown that BaCuQF (Q = S, Se) compounds have a considerably large carrier mobility compared with most TCOs.17–19 Further, it has been observed that the electronegativity and size of the anion influence the bonding characteristics and structures of such materials, which determine the p-type performance.20 Studies of the intrinsic and substitutional defects in BaCuChF (Ch = S, Se, Te) based compounds have revealed unintentional p-type conductivity owing to the presence of Cu vacancies.21,22 The optoelectronic properties of BAMChF (A = Sr, Ba; M = Cu, Ag; and Ch = S, Se, Te) based chalcogenide fluorides have been found to vary with atomic substitution or with vacancy formation.23 Chalcogenide-based compounds have been found to exhibit a larger carrier mobility than oxides.24,25
The majority of experimental studies and ab initio calculations performed so far have analyzed the p-type performance of Ba- and Cu-based ternary and quaternary chalcogenides and oxides. Until now, the question remains open as to whether alternative chemistries and design rules could lead to the discovery of promising transparent materials with low hole effective masses. Addressing this question plays a dominant role in the TCM field, with the aim of rationally designing materials sought by the optoelectronic industry. Recently, high-throughput density functional theory (DFT) approach has been employed for non-oxide binary semiconductors and found boron phosphide (BP) to be a promising p-type TCM candidate.26 Their work has opened up a new direction of investigation into binary non-oxide TCMs. However, an in-depth understanding of the factors that influence the p-type performance of these materials is still required.
In this work, we performed high-throughput DFT calculations for chalcogenide-based binary semiconductors to identify the most promising p-type transparent conductors. Our material screening strategy led to the identification of nine potential p-type transparent conductors (ZnS, ZnSe, ZnTe, MgS, MgTe, GaSe, GaTe, Al2Se3, and BeTe). In addition, we proposed strategies to alter the electronic structure of the materials through material engineering approach. As an example, we demonstrated how to tune the electronic properties of GeS so that it can be employed as a p-type TCM.
2 Computational details
2.1 DFT calculations
All DFT calculations were performed using the Vienna Ab initio Simulation Package (VASP)27 with PAW pseudopotentials28,29 and a plane-wave cutoff of 500 eV. The exchange correlation is described with the Perdew–Burke–Ernzerhof (PBE)30 form of the generalized gradient approximation for structural optimization. All the atoms in the system were allowed to relax until the force on each atom was less than 0.01 eV Å−1. Brillouin zone integration was performed on a Monkhorst k-point mesh. We adapted the k-mesh of each supercell to maintain a constant k-point density for each system. Since PBE functional tends to underestimate the band gaps of semiconductors, we employed the HSE06 screened hybrid functional (HSE)31 to calculate the band structures and hole effective masses of selected compounds. Effective masses were calculated using the EMC code.32 We first determined the top of the valence band for each compound. Then, the EMC code has been employed to evaluate ∂2E/∂kikj (i, j = x, y, and z) numerically using the finite difference method. The effective mass tensor is calculated from this derivative. For non-cubic systems we calculated the band structure along the high-symmetry directions as well. Assuming the valence band has a parabolic shape in the small area close to the VBM, we calculated the aforementioned derivative by curve fitting. We note in passing that we compared our calculated effective masses with those calculated by BoltzTraP code33 and found a reasonable agreement although the methods are different.The supercell calculation is the most common method to calculate the formation energy of defects.34 In this method a defect α with the charge state q is introduced into the supercell. The periodic boundary is held by repeating the supercell periodically in x, y, and z directions. The dimension of the supercell has to be rather large to reduce the spurious interactions between a defect and its periodic replicas.35 In this work defect formation energies and the corresponding charge transition states were calculated on large supercells (more than 100 atoms) in order to minimize finite-size effects. The formation energy of a defect is defined as
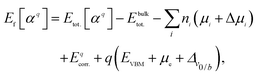 | (1) |
In order to ensure the validity of our approach and results, we performed calculations for our final compounds with the recently developed PyCDT script.38 This script gets the atomic structure and formation energies of the compounds from the Materials Project (MP) database.39 The correction terms are calculated based on the Freysoldt approach.40 As it is expected,36 there is a very good agreement between the results achieved by two approaches.
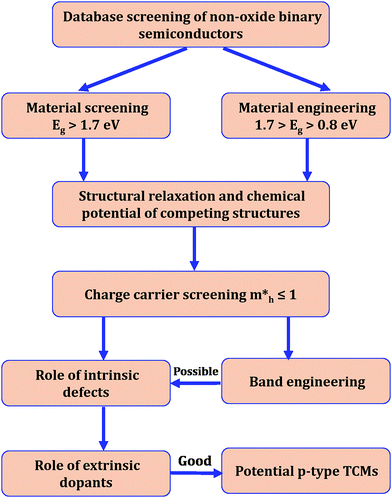
2.2 Material screening and engineering strategy
High-throughput computational screening was performed to identify potential transparent conductors. Further, the electronic and optical properties of selected compounds were tuned by material engineering. Our approach utilized data mining of chalcogenide-based non-oxide binary semiconductors that have already been synthesized and documented in the literature.41 The crystalline structures of the binary compounds were obtained from the Inorganic Crystal Structure Database (ICSD) or Materials Project database.39 Our screening strategy is based on the flowchart depicted in Fig. 1. The following steps were followed for the rational design of materials that are potential p-type candidates:3 Results and discussion
Our study focused on material screening and material engineering for optoelectronic applications. Our criteria for material screening were as follows: materials with Eg > 1.7 eV (the minimum value needed for Cu(In, Ga)Se2-based tandem cells45) and a hole effective mass <1. Among 500 compounds, we found less than 40 chalcogenides that satisfied our screening criterion for Eg. The calculated hole effective mass versus the experimentally measured band gap for some compounds with hole effective masses of <3 are shown in Fig. 2. We divided the compounds into three groups: group A compounds satisfy our screening criteria for Eg and hole effective mass. The compounds to the left of the vertical green line (group B) have low hole effective masses but Eg is too small whereas the compounds above the horizontal green line (group C) have large Eg value but their hole effective masses are larger than 1. Material engineering was carried out to overcome the deficiencies in the group B and C compounds.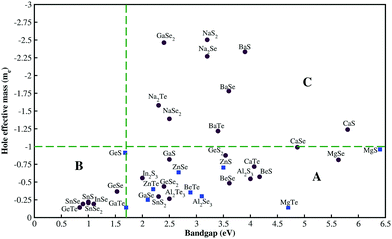 | ||
| Fig. 2 Experimentally measured band gap41vs. calculated hole effective mass. Blue squares indicate the materials we suggest for p-type TCM applications. Red circles show materials that are not suitable for high-performance TCMs either owing to a small band gap (group B), or a large hole effective mass (group C), or the lack of dopability. | ||
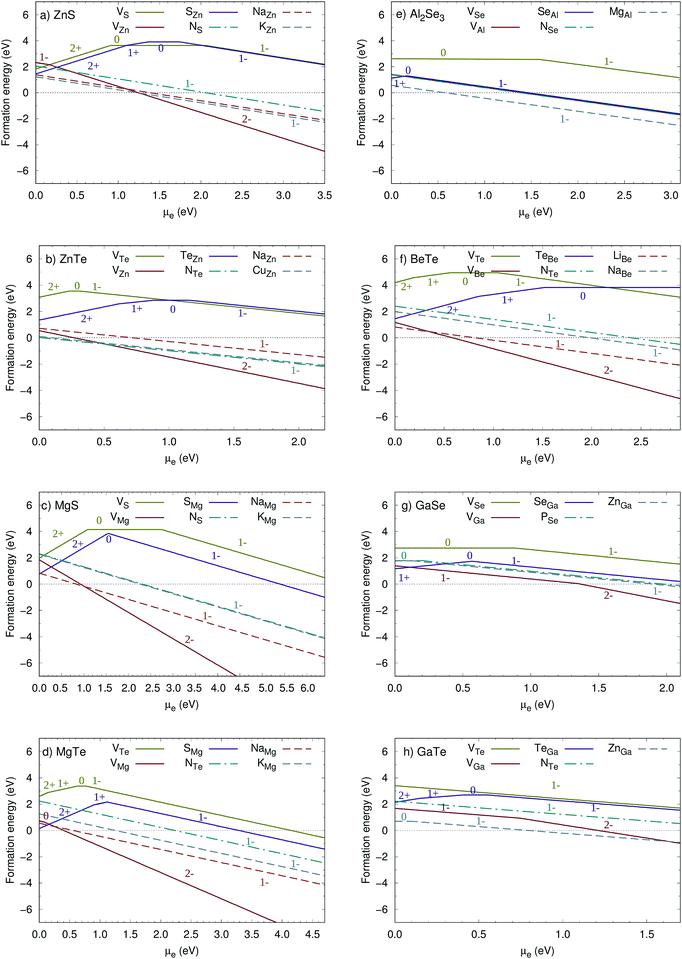
We further examined the dopability of the group A compounds by introducing intrinsic defects such as vacancies and antisites. Anion vacancies are usually donor defects that compensate for the holes provided by acceptor-like defects. The p-type dopability of a material depends predominantly on the formation of anion vacancies. It is possible to hinder the formation of anion vacancies during synthesis by controlling the chemical potential of the elements. Anion-rich conditions impede the formation of anion vacancies, but can also lead to the formation of antisites. Hence, we calculated the intrinsic defect formation energies under anion-rich conditions.
Among the various chalcogenides, only a few compounds were found to uphold the intrinsic defects. For example, cubic CaTe (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) has a wide Eg (∼4 eV)46 and a relatively small hole effective mass (0.72). Despite its promising electronic properties, the formation of TeCa antisites in CaTe compensated for the holes generated by VCa. We neglected compounds from group A whose hole-compensating defects have low formation energies (red circles in Fig. 2).
m) has a wide Eg (∼4 eV)46 and a relatively small hole effective mass (0.72). Despite its promising electronic properties, the formation of TeCa antisites in CaTe compensated for the holes generated by VCa. We neglected compounds from group A whose hole-compensating defects have low formation energies (red circles in Fig. 2).
The materials we considered here demonstrated propensity for increased anion vacancy formation energy and decreased cation vacancy formation energy on moving from sulfides to tellurides. For example, in ZnTe, the formation of anion vacancies is about 1.2 eV larger than that in ZnS. Further, cation vacancies are more favorable in ZnTe than in ZnS or ZnSe. Similar trends were observed for antisite defects, although the change in formation energies is much smaller. From these trends, we cannot say a priori whether tellurides are better candidates for p-type TCMs than sulfides. While lower anion vacancies in tellurides are beneficial for hole conductivity, the formation of donor-like antisites can be detrimental for p-type conductivity.
Another vital prerequisite for high-performance TCMs is plausibility of doping with dopants that enhance the free-carrier density in the system. Regardless of the possibility that the intrinsic defects will increase the hole concentration, a TCM must be doped to improve performance. Therefore, we doped our compounds that showed good p-type dopability. We also studied the p-type doping properties of compounds for which the formation energy of intrinsic defects is high, even if they did not show the desired properties. A potential p-type TCM candidate may also exhibit considerably lower formation energy for some p-type dopants compared with intrinsic defects.
When dopants are incorporated into the host semiconductor, depending on experimental conditions, the chemical potentials of the dopant are subject to specific bounds.47 We considered two extreme limits in our calculations, namely when the dopants are in the elemental phases, and when the chemical potentials of dopants are bounded by avoiding the formation of the secondary phases. The upper limits for the chemical potential of dopants to avoid the formation of the secondary phases are listed in the ESI.† In practice, the chemical potentials of dopants vary between these two limits depending on the experimental conditions. In Fig. 3, the formation energies of extrinsic defects under the later condition are shown. The formation energies under the former condition are shown in the ESI.†
We found nine chalcogenides that satisfied the above-mentioned criteria and could be employed as p-type TCMs (blue squares in Fig. 2). The compounds, their symmetries, calculated/measured band gaps, and calculated hole effective masses are listed in Table 1. We note that these compounds have different atomic and electronic structures. The required application determines whether a layered-structure compound (GaSe) or a symmetric structure (ZnTe) is desirable. The following sections outline the properties of the most promising p-type TCM candidates.
3.1 Zn-Based chalcogenides
Zinc chalcogenides have zincblende atomic structure (F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m). The electronic structures of ZnS, ZnSe, and ZnTe are very similar, namely, the top of the valence band is at the Γ point and has mainly anion p character with a small contribution from Zn. The band gaps and hole effective masses of Zn chalcogenides decrease with decreasing anion electronegativity (Fig. 2).
3m). The electronic structures of ZnS, ZnSe, and ZnTe are very similar, namely, the top of the valence band is at the Γ point and has mainly anion p character with a small contribution from Zn. The band gaps and hole effective masses of Zn chalcogenides decrease with decreasing anion electronegativity (Fig. 2).
ZnS is a direct band gap semiconductor with a wide measured Eg of 3.7 eV.48 When the Fermi level was close to the valence band maximum (VBM), hole-compensating defects formed more easily than cation vacancies (Fig. 3a). The formation energy of cation vacancies, however, decreased rapidly as the electron chemical potential μe increased. Considering the intrinsic defects, ZnS is not a promising p-type conductor.55 However, the role of extrinsic dopants for ZnS was explored owing to its promising electronic properties. We observed that extrinsic dopants such as Na and K for Zn, as well as N for S, increase the hole concentration. The formation energies for these defects were found to be smaller than those for intrinsic defects. It has been reported that the transparency and conductivity of Cu-doped ZnS are satisfactory for a p-type TCM.56,57 In agreement with the previous results, we also found that CuZn acts as an acceptor and increases the hole concentration. Doping with the suggested alkali metals will give rise to better p-type conductivity by preventing the formation of intrinsic antisite defects. NS defects, on the other hand, will prevent the formation of hole-compensating anion vacancies.
In ZnTe, cation vacancies formed more easily than anion vacancies and antisites (Fig. 3b). Cation vacancies introduced holes into the system and improved conductivity in ZnTe. Antisites and anion vacancies impacted the transport properties of ZnTe. However, the formation energies of these intrinsic defects were too high. Similar to ZnS, ZnTe could also be doped with Na, Cu, and N. NaZn, CuZn, and NTe substitutional defects had low formation energies and formed easily in ZnTe. Cu-doped ZnTe films and nanowires have been synthesized previously and show good p-type conductivity and transparency.58,59 In this respect, our results are in agreement with experimental observations. The behavior of ZnSe falls between that of ZnS and ZnTe (ESI,† Fig. S2). There are several reports on the good conductivity of p-doped ZnSe60,61 and our results agree well with the reported observations. We found Zn-based chalcogenides to be promising p-type candidates.
3.2 Mg-Based chalcogenides
Mg-Based chalcogenides have wide band gaps, which is the primary requirement for optoelectronic applications. Cubic MgS has an indirect Eg of 6.4 eV,51 whereas hexagonal MgTe has a direct band gap of 4.7 eV52 (Fig. S5 of the ESI†). In order to understand defect physics in these compounds, we examined the influence of point defects on the carrier concentration. The formation of intrinsic defects was less likely in MgS than in MgTe (Fig. 3c and d). Although both materials had small hole densities without doping, Na- or K-doped MgS and MgTe are good candidates for p-type conductors. Adding these alkali metals to these systems led to the formation of NaMg and KMg substitutional acceptor defects. Anion substitutional defects (NS and NTe) also resulted in acceptor defects in these compounds. The VBM of MgS consists of p states of the anion with a hole effective mass of 0.96. By substituting S with Te, the characteristics of the VBM did not change, but the effective mass and Eg decreased. We also studied MgS with the zinc-blende structure (F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m). In contrast to MgS with the Fm
3m). In contrast to MgS with the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetry, zinc-blende MgS is not a good candidate for p-type TCMs owing to easy formation of donor-like defects.
m symmetry, zinc-blende MgS is not a good candidate for p-type TCMs owing to easy formation of donor-like defects.
Our results indicate that with intentional doping, MgS and MgTe could be used as a high-performance TCMs. To the best of our knowledge, Mg-based chalcogenides have not been considered so far as p-type TCMs. In contrast to MgS and similar to other layered-structure materials, the effective mass of MgTe is anisotropic. While the hole effective mass is as small as 0.18 parallel to the layers, it is 8.06 perpendicular to the layers. It has been shown that depending on the growth conditions, the orientation of the layers in layered-structure materials can be controlled.62 This property gives a degree of freedom in designing devices to control the conductivity in the preferred direction.
3.3 Al-Based chalcogenides
Al2Se3 has a wide direct band gap (Eg = 3.1 eV)41 (Fig. S6 of the ESI†). The top of the valence band has mainly Se p character and is very close to the Γ point. This band structure results in a rather low hole effective mass of 0.30. The formation of anion vacancies generated transition states at about 0.60 eV above the VBM (Fig. 3e). Antisite and cation vacancies had low formation energies compared with anion vacancies. However, the intrinsic defects in Al2Se3 have very high formation energies and consequently their concentrations are low. In contrast to intrinsic defects, NSe and MgAl substitutional defects had low formation energies and both defects were beneficial for p-type conductivity. PSe was also an acceptor dopant, but the formation energy of this defect was comparable to those of intrinsic defects (not shown here). Al2Se3 has a wurtzite-type structure with four ordered Al vacancies per unit cell. Owing to this symmetry, the effective mass of this compound is anisotropic (0.30, 2.71, and 3.33). This anisotropy is less pronounced in devices where TCMs are grown as polycrystalline films.Replacing Se with Te resulted in a smaller Eg and hole effective mass in Al2Te3. The formation of antisites was more favorable in Al2Te3 than in Al2Se3. In contrast to Al2Se3, cation vacancies created charge transition levels in the band gap of Al2Te3. Although these defects hindered p dopability, substitutional dopants such as MgAl and NTe could be employed to improve the hole conductivity of Al2Te3. Al2S3 has a larger band gap and better p-dopability than Al2Se3. Nevertheless, we could not find an appropriate dopant to increase the hole concentration in Al2S3. Hence, among aluminum chalcogenides, Al2Se3 was found to be the most promising candidate.
3.4 Be-Based chalcogenides
BeTe is an indirect band gap semiconductor with a large band gap (Eg = 2.9 eV)41 and a small hole effective mass of 0.35. Similar to other good candidates, the VBM consists of p states. Without doping, BeTe is a potential p-type conductor because the formation energies for cation vacancies are low compared with other intrinsic defects (Fig. 3f). To enhance the hole conductivity, BeTe was intentionally doped with Li, Na, and N atoms. LiBe has low formation energies when the Fermi level is at the VBM. This defect is an acceptor and increases the hole concentration in the valence band. BeS has a larger band gap and hole effective mass than BeTe. Antisite defects were detrimental for p-type conductivity in BeS. Doping with alkali metals was also not beneficial since the formation energies were comparable to those of antisites. Hence, BeTe was found to be the most promising candidate among the various Be-based chalcogenides.3.5 Ga-Based chalcogenides
GaSe is another chalcogenide that has a low hole effective mass and relatively large band gap (2.1 eV).53 The VBM of GaSe has p character, which is a mixture of the Ga and Se p states. Anion vacancies and antisites acted as donors at small electron chemical potentials and created transition levels in the band gap (Fig. 3g). Cation vacancies created a transition state in the band gap. All interstitial defects had relatively high formation energies and consequently low concentrations in GaSe. GaSe could be doped with P and Zn to enhance the p-type conductivity. ZnGa and PSe defects created shallow acceptor levels. It has been shown experimentally that Zn enhances the hole conductivity of GaSe,63 which is also evident from our calculations.Replacing Se with S resulted in a wider band gap and larger effective mass. The dopability of GaS is worse than that of GaSe owing to the formation of anion vacancies rather than cation vacancies. ZnGa and NS substitutional defects in GaS remained neutral and were not beneficial for p-type conductivity. Replacing Se with Te, on the other hand, increased the probability of cation vacancy formation in GaTe. Although cation vacancies are acceptor defects, they are harmful for conductivity since they create charge transition levels in the band gap. To enhance the hole conductivity, GaTe can be doped with Zn and N (Fig. 3h). The size of the band gap and hole effective mass decreases in Ga chalcogenides from GaS to GaTe. Despite the low effective mass and good dopability of GaTe, it is not suitable for many optoelectronic applications owing to its small band gap. For this reason, we investigated GaTe and similar compounds from the band engineering perspective as discussed in the next section. We note in passing that the effective masses of GaSe and GaTe are anisotropic owing to the crystal symmetry. GaSe and GaTe are layered compounds and the effective masses are small parallel to the layers; 0.30 and 0.14 for GaSe and GaTe, respectively. The values of effective mass perpendicular to the layers are 1.78 and 18.92 for GaSe, and 0.91 and 10.01 for GaTe.
4 Band engineering
4.1 Role of the layer thickness
Band gap modulation can be achieved for layered compounds by tuning the layer thickness.64–66 Here, we investigated the electronic and optical properties of the group B compounds (Fig. 2) as a function of the layer thickness. As shown in Table 2, Eg shows an increasing trend with a reduction in the layer thickness. The change in the band gap size could be as large as 60% for SnS. As an example, we show the modulation of the band gap of GeS with the layer thickness (Fig. S3 of the ESI†). Reducing the layers of GeS widened the band gap and at the same time induced a direct to indirect band gap transition.| Compound | E HSEg (eV) | |||
|---|---|---|---|---|
| Monolayer | Bilayer | 4 layers | Bulk | |
| SnS | 2.26 | 1.63 | 1.60 | 1.41 |
| SnSe | 1.65 | 1.49 | 1.45 | 1.10 |
| GeS | 2.50 | 2.20 | 1.96 | 1.85 |
| GeSe | 1.80 | 1.86 | 1.60 | 1.40 |
| GeTe | 1.23 | — | — | 1.07 |
| GaTe | 2.38 | 1.84 | 1.63 | 1.50 |
Changes in the hole effective masses were comparatively predominant in Ge-based compounds (Table S2 of the ESI†). Although Te-based compounds normally have smaller hole effective masses than sulfides, the band gap modulation was less effective in Te-based compounds and most promising in S-based compounds. These results show that anions influence the optoelectronic properties significantly. We doped two S-based compounds (GeS and SnS) that showed large band gap modulation with the layer thickness to understand the defect physics. In GeS, cation vacancies had lower formation energies than anion vacancies and antisites (Fig. S4 of the ESI†). In contrast, for SnS, the anion vacancies and antisites had lower formation energies than cation vacancies, which hindered the performance. Further, extrinsic dopants, such as NaGe and NS, were found to increase the hole concentration in GeS. These results indicate that by controlling the layer thickness and by substitutional doping, GeS can be considered as a promising p-type TCM.
4.2 External stress
In devices, TCMs are normally used as thin films. The lattice parameters of epitaxially grown films are either compressed or expanded owing to lattice mismatch. Normally, for materials under pressure, when the lattice parameters are compressed, the valence band becomes more disperse, which results in a smaller hole effective mass.44,67,68 This change in the electronic structure by stress can be used to enhance hole conductivity. If TCM films are grown coherently on substrates in such a way that the lattice parameters of the film are compressed, then one expects to observe a smaller hole effective mass. We studied the evolution of the optoelectronic properties of a few compounds in groups A and C (Fig. 2) when the lattice parameters were compressed. The lattice parameters of MgS, CaSe, Na2Te, and BaTe were compressed by about 5% and the effective mass was calculated. The changes in the effective masses were about 9% for Na2Te and about 15% for MgS, CaSe, and BaTe. We suggest that this strategy can be employed for reducing the hole effective mass further to improve the performance of p-type TCMs.5 Concluding remarks
Data mining and high-throughput calculations were performed to identify high-performance p-type TCMs. Our criteria for material selection are a band gap larger than 1.7 eV and a hole effective mass smaller than 1. Our calculations suggested nine promising p-type TCM candidates (ZnS, ZnSe, ZnTe, MgS, MgTe, GaSe, GaTe, Al2Se3, and BeTe). The VBM for the promising candidates consists of anion p states, which demonstrates the importance of the anions in p-type TCMs. For a particular cation, the anion vacancy formation energies were found to increase from sulfides to tellurides, whereas the formation energies of the cation vacancies and antisites decreased. We showed that with intentional external doping, some of the compounds with high-energy intrinsic defects could be promising p-type TCMs. In addition, material engineering was carried out for materials with Eg < 1.7 eV or a hole effective mass larger than 1. It was observed that the optoelectronic properties of a material could be modulated by tuning the layer thickness and external stress.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge financial support from the German Bundesministerium für Wirtschaft und Energie (BMWi) for the speedCIGS project (0324095C). The authors gratefully acknowledge the Gauss Centre for Supercomputing e.V. (http://www.gauss-centre.eu) for funding this project by providing computing time on the GCS Supercomputer SuperMUC at Leibniz Supercomputing Centre (http://www.lrz.de). Open Access funding provided by the Max Planck Society.References
- K. Ellmer, Nat. Photonics, 2012, 6, 809–817 CrossRef CAS.
- E. Fortunato, D. Ginley, H. Hosono and D. C. Paine, MRS Bull., 2007, 32, 242–247 CrossRef CAS.
- D. Ginley, H. Hosono and D. C. Paine, Handbook of Transparent Conductors, Springer, New York, 3rd edn, 2011 Search PubMed.
- C. G. Granqvist, Sol. Energy Mater. Sol. Cells, 2007, 91, 1529–1598 CrossRef CAS.
- P. Yu and M. Cardona, Fundamentals of Semiconductors, 2010 Search PubMed.
- R. G. Gordon, MRS Bull., 2000, 25, 52–57 CrossRef CAS.
- X. Yu, T. J. Marks and A. Facchetti, Nat. Mater., 2016, 15, 383–396 CrossRef CAS PubMed.
- G. Hautier, A. Miglio, G. Ceder, G.-M. Rignanese and X. Gonze, Nat. Commun., 2013, 4, 3292–3297 Search PubMed.
- M. Morales-Masis, S. De Wolf, R. Woods-Robinson, J. W. Ager and C. Ballif, Adv. Electron. Mater., 2017, 3, 1600529 CrossRef.
- K. P. Loh, Q. Bao, G. Eda and M. Chhowalla, Nat. Chem., 2010, 2, 1015–1024 CrossRef CAS PubMed.
- H. Kawazoe, M. Yasukawa, H. Hyodo, M. Kurita, H. Yanagi and H. Hosono, Nature, 1997, 389, 939–942 CrossRef CAS.
- K. Ueda, S. Inoue, S. Hirose, H. Kawazoe and H. Hosono, Appl. Phys. Lett., 2000, 77, 2701–2703 CrossRef CAS.
- G. Hautier, A. Miglio, D. Waroquiers, G.-M. Rignanese and X. Gonze, Chem. Mater., 2014, 26, 5447–5458 CrossRef CAS.
- A. Bhatia, G. Hautier, T. Nilgianskul, A. Miglio, J. Sun, H. J. Kim, K. H. Kim, S. Chen, G.-M. Rignanese, X. Gonze and J. Suntivich, Chem. Mater., 2016, 28, 30–34 CrossRef CAS.
- N. Sarmadian, R. Saniz, B. Partoens and D. Lamoen, Sci. Rep., 2016, 6, 20446–20455 CrossRef CAS PubMed.
- K. H. L. Zhang, K. Xi, M. G. Blamire and R. G. Egdell, J. Phys.: Condens. Matter, 2016, 28, 383002 CrossRef PubMed.
- H. Yanagi, J. Tate, S. Park, C.-H. Park and D. A. Keszler, Appl. Phys. Lett., 2003, 82, 2814 CrossRef CAS.
- H. Yanagi, J. Tate, S. Park, C.-H. Park, D. A. Keszler, K. M. Hirano and H. Hosono, J. Appl. Phys., 2006, 100, 083705 CrossRef.
- R. Kykyneshi, D. H. MeIntyre, J. Tate, C.-H. Park and D. A. Keszler, J. Solid State Chem., 2006, 179, 1668–1673 CrossRef.
- K. Feng, W. Yin, Z. Lin, J. Yao and Y. Wu, Inorg. Chem., 2013, 52, 11503–11508 CrossRef CAS PubMed.
- A. Zakutayev, R. Kykyneshi, G. Schneider, D. H. McIntyre and J. Tate, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 155103 CrossRef.
- A. Zakutayev, J. Tate and G. Schneider, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 195204 CrossRef.
- V. V. Bannikov, I. R. Shein and A. L. Ivanovskii, J. Solid State Chem., 2012, 196, 601–606 CrossRef CAS.
- S. Hongliang, S. Bayrammurad, S. J. David, S. S. Athena and D. Mao-Hua, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 184104 CrossRef.
- Y. Feng, Z. Xiuwen, Y. G. Yonggang, Y. Liping, N. Arpun, M. O. Thomas and Z. Alex, Nat. Commun., 2015, 6, 7308 CrossRef PubMed.
- J. B. Varley, A. Miglio, V.-A. Ha, M. J. van Setten, G.-M. Rignanese and G. Hautier, Chem. Mater., 2017, 29, 2568–2573 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- P. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- A. Fonari and C. Sutton, Effective Mass Calculator for Semiconductors, 2012, https://github.com/afonari/emc Search PubMed.
- G. K. Madsen and D. J. Singh, Comput. Phys. Commun., 2006, 175, 67–71 CrossRef CAS.
- E. Ghorbani, J. Kiss, H. Mirhosseini, G. Roma, M. Schmidt, J. Windeln, T. D. Kühne and C. Felser, J. Phys. Chem. C, 2015, 119, 25197–25203 CAS.
- S. B. Zhang, S.-H. Wei, A. Zunger and H. Katayama-Yoshida, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 9642–9656 CrossRef CAS.
- H.-P. Komsa, T. T. Rantala and A. Pasquarello, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 045112 CrossRef.
- S. Lany and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 235104 CrossRef.
- D. Broberg, B. Medasani, N. Zimmermann, A. Canning, M. Haranczyk, M. Asta and G. Hautier, 2017, arXiv:1611.07481.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and A. K. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- C. Freysoldt, J. Neugebauer and C. G. Van de Walle, Phys. Rev. Lett., 2009, 102, 016402 CrossRef PubMed.
- W. H. Strehlow and E. H. Cook, J. Phys. Chem. Ref. Data, 1973, 2, 163–199 CrossRef CAS.
- C. L. Gomes and A. Carvalho, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 085406 CrossRef.
- C. Chowdhury, S. Karmakar and A. Datta, J. Phys. Chem. C, 2017, 121, 7615–7624 Search PubMed.
- K. P. Dhakal, S. Roy, H. Jang, X. Chen, W. S. Yun, H. Kim, J. Lee, J. Kim and J.-H. Ahn, Chem. Mater., 2017, 29, 5124–5133 CrossRef CAS.
- P. Mantilla-Perez, T. Feurer, J.-P. Correa-Baena, Q. Liu, S. Colodrero, J. Toudert, M. Saliba, S. Buecheler, A. Hagfeldt, A. N. Tiwari and J. Martorell, ACS Photonics, 2017, 4, 861–867 CrossRef CAS.
- G. A. Saum and E. B. Hensley, Phys. Rev., 1959, 113, 1019–1022 CrossRef CAS.
- C. Freysoldt, B. Grabowski, T. Hickel, J. Neugebauer, G. Kresse, A. Janotti and C. G. Van de Walle, Rev. Mod. Phys., 2014, 86, 253–305 CrossRef.
- A. Kudo and Y. Miseki, Chem. Soc. Rev., 2009, 38, 253–278 RSC.
- M. F. Al-Kuhaili, A. Kayani, S. M. A. Durrani, I. A. Bakhtiari and M. B. Haider, ACS Appl. Mater. Interfaces, 2013, 5, 5366–5372 CAS.
- J. Wang and M. Isshiki, in Wide-Bandgap II-VI Semiconductors: Growth and Properties, ed. S. Kasap and P. Capper, Springer US, Boston, MA, 2007, pp. 325–342 Search PubMed.
- R. Pandey, J. E. Jaffe and A. B. Kunz, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 9228–9237 CrossRef CAS.
- M. Inoue, J. Phys. Soc. Jpn., 1969, 26, 1186–1195 CrossRef CAS.
- C. S. Jung, F. Shojaei, K. Park, J. Y. Oh, H. S. Im, D. M. Jang, J. Park and H. S. Kang, ACS Nano, 2015, 9, 9585–9593 CrossRef CAS PubMed.
- U. Giorgianni, G. Mondio, P. Perillo, G. Saitta and G. Vermiglio, J. Phys., 1977, 38, 1293–1299 CAS.
- P. Li, S. Deng, L. Zhang, G. Liu and J. Yu, Chem. Phys. Lett., 2012, 531, 75–79 CrossRef CAS.
- A. M. Diamond, L. Corbellini, K. R. Balasubramaniam, S. Chen, S. Wang, T. S. Matthews, L.-W. Wang, R. Ramesh and J. W. Ager, Phys. Status Solidi A, 2012, 209, 2101–2107 CrossRef CAS.
- X. Xu, J. Bullock, L. T. Schelhas, E. Z. Stutz, J. J. Fonseca, M. Hettick, V. L. Pool, K. F. Tai, M. F. Toney, X. Fang, A. Javey, L. H. Wong and J. W. Ager, Nano Lett., 2016, 16, 1925–1932 CrossRef CAS PubMed.
- L. Feng, D. Mao, J. Tang, R. T. Collins and J. U. Trefny, J. Electron. Mater., 1996, 25, 1422–1427 CrossRef CAS.
- H. B. Huo, L. Dai, C. Liu, L. P. You, W. Q. Yang, R. M. Ma, G. Z. Ran and G. G. Qin, Nanotechnology, 2006, 17, 5912 CrossRef CAS.
- A. Yahata, H. Mitsuhashi, K. Hirahara and T. Beppu, Jpn. J. Appl. Phys., 1990, 29, L4 CrossRef CAS.
- H. S. Song, W. J. Zhang, G. D. Yuan, Z. B. He, W. F. Zhang, Y. B. Tang, L. B. Luo, C. S. Lee, I. Bello and S. T. Lee, Appl. Phys. Lett., 2009, 95, 033117 CrossRef.
- J. H. Yu, H. R. Lee, S. S. Hong, D. Kong, H.-W. Lee, H. Wang, F. Xiong, S. Wang and Y. Cui, Nano Lett., 2015, 15, 1031–1035 CrossRef CAS PubMed.
- S. Shigetomi, T. Ikari, H. Nakashima and H. Nishimura, Phys. Status Solidi A, 1991, 128, K95–K98 CrossRef CAS.
- J. N. Coleman, M. Lotya, A. O'Neill, S. D. Bergin, P. J. King, U. Khan, K. Young, A. Gaucher, S. De, R. J. Smith, I. V. Shvets, S. K. Arora, G. Stanton, H.-Y. Kim, K. Lee, G. T. Kim, G. S. Duesberg, T. Hallam, J. J. Boland, J. J. Wang, J. F. Donegan, J. C. Grunlan, G. Moriarty, A. Shmeliov, R. J. Nicholls, J. M. Perkins, E. M. Grieveson, K. Theuwissen, D. W. McComb, P. D. Nellist and V. Nicolosi, Science, 2011, 331, 568–571 CrossRef CAS PubMed.
- H. Mirhosseini, G. Roma, J. Kiss and C. Felser, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 205301 CrossRef.
- A. Arora, K. Nogajewski, M. Molas, M. Koperski and M. Potemski, Nanoscale, 2015, 7, 20769–20775 RSC.
- H. J. Conley, B. Wang, J. I. Ziegler, R. F. Haglund, S. T. Pantelides and K. I. Bolotin, Nano Lett., 2013, 13, 3626–3630 CrossRef CAS PubMed.
- M. A. ElGhazali, P. G. Naumov, H. Mirhosseini, V. Süβ, L. Müchler, W. Schnelle, C. Felser and S. A. Medvedev, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 96, 060509 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7tc05311h |
| This journal is © The Royal Society of Chemistry 2018 |