Unravelling the role of electron–hole pair spin in exciton dissociation in squaraine-based organic solar cells by magneto-photocurrent measurements†
Abstract
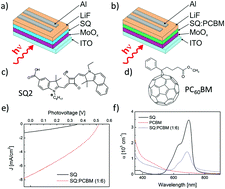
A high absorption coefficient and narrow absorption bands in squaraine (SQ) dyes have resulted in rapidly growing interest in them as a donor material in photovoltaic devices. The exciton dissociation process in organic systems proceeds via a multistep mechanism where the electron–hole pairs (charge transfer states) involved in the current generation process determine the recombination losses and subsequently limit the overall performance of organic solar cells. In this work, these basic electronic processes are investigated by magneto-photocurrent measurements (MPC, the photocurrent change induced by the external magnetic field) of SQ:PC60BM bulk-heterojunction solar cells with varying electron acceptor concentrations under magnetic fields up to 9 T and at different temperatures. Under a weak external magnetic field, the change in photocurrent is due to electron and hole (e–h) pairs that experience a modulating hyperfine interaction associated with nuclear (mainly proton) magnetic moment, while in strong magnetic fields the photocurrent is affected by the Δg mechanism with spin dephasing due to different Lande factors of the electron and hole entities (Δg ≈ 10−3). To consistently interpret the amplitudes and lineshapes of the MPC signals at various temperatures, charge carrier hopping in a disordered environment competing with the magnetic dipole spin precession is proposed. The requirements for efficient small-molecular weight organic:fullerene bulk-heterojunction solar cells are briefly discussed.


 Please wait while we load your content...
Please wait while we load your content...