Silk fibroin as a biotemplate for hierarchical porous silica monoliths for random laser applications†
Abstract
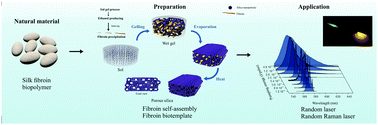
Bombyx mori silk fibroin offers unlimited opportunities for functionalization, processing, and biological integration. We describe in this work the design of structured organic inorganic hybrids based on silica and silk fibroin, taking advantage of the relationship between the structure and processing of the latter. In situ self-assembly of fibroin nanofibers along with hydrolysis and polycondensation of tetraethyl orthosilicate was employed. Structural characterization was performed by Raman and solid state NMR spectroscopies. Our findings demonstrated that fibroin precipitates in the reaction medium with prevailing β-sheet conformation. The transition from amorphous to crystalline state was observed to be favored by the increase of the fibroin concentration in the samples. The samples were obtained as robust and biocompatible monoliths, making them candidates for several applications, particularly in the biomedical field. As a novel development, the fibroin nanofibers were used as pore biotemplates to create mechanically robust silica monoliths with a hierarchical macro-mesoporous network in an easy templating process. The template was removed by thermal treatment and the as obtained silica based materials displayed surface area values ranging from 704 to 1057 m2 g−1 and a maximum pore volume of 0.621 mL g−1. The porous silica monoliths were then doped with rhodamine 6G and typical random laser action could be observed, with a minimum laser threshold of 9.7 μJ per pulse and a linewidth narrowing from 40 to 4 nm. In addition, it was shown that two coupled gain mechanisms were taking place, the random lasing and the stimulated Raman scattering, allowing us to observe Raman Stokes lines due to vibrational modes of the dye molecule.
- This article is part of the themed collection: Materials and Nano Research in Brazil


 Please wait while we load your content...
Please wait while we load your content...