Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
First-principles insights into tin-based two-dimensional hybrid halide perovskites for photovoltaics†
Zhenyu
Wang
abc,
Alex M.
Ganose
 bcd,
Chunming
Niu
a and
David O.
Scanlon
bcd,
Chunming
Niu
a and
David O.
Scanlon
 *bcd
*bcd
aXi'an Jiaotong University, Center of Nanomaterials for Renewable Energy, State Key Lab of Electrical Insulation and Power Equipment, School of Electrical Engineering, 99 Yanxiang Road, Xi'an 710054, China
bDepartment of Chemistry, University College London, 20 Gordon Street, London WC1H 0AJ, UK. E-mail: d.scanlon@ucl.ac.uk
cThomas Young Centre, University College London, Gower Street, London WC1E 6BT, UK
dDiamond Light Source Ltd., Diamond House, Harwell Science and Innovation Campus, Didcot, Oxfordshire OX11 0DE, UK
First published on 13th March 2018
Abstract
The two-dimensional (2D) hybrid halide perovskites have recently attracted attention due to their excellent photovoltaic performance. In comparison to their three-dimensional (3D) analogues, they show superior long-term durability and moisture tolerance. Meanwhile, their layered topology offers greater flexibility for electronic structure tuning. To date, most devices containing 2D perovskites have been based on Pb, which presents environment concerns and a possible roadblock to commercialisation due to its toxicity. The development of lead-free alternatives is therefore immensely important to facilitate the uptake of perovskite-based photovoltaics. Herein, we investigate the geometrical, electronic and optical properties of the semiconducting 2D tin perovskites (CH3(CH2)3NH3)2(CH3NH3)n−1SnnI3n+1 (n = 1, 2 and 3), using relativistic hybrid density functional theory calculations. We demonstrate that the band gaps of the series decrease with increasing perovskite-like layer thickness, from 1.85 eV (n = 1) to 1.38 eV (n = 3). We find strong and broad optical absorption across the series, in addition to small effective masses of electrons and holes in the laminar plane. The n = 3 composition displays a high spectroscopic limited maximum efficiency of 24.6%. Our results indicate this series of homologous 2D tin halide perovskites are a promising class of stable and efficient light-absorbing materials for photovoltaics.
Introduction
The drive towards reduced costs, higher conversion efficiencies and environmentally friendly alternatives to current photovoltaic technologies is immensely important in the search to relieve the world's reliance on fossil fuels and promote sustainable economic development.1–3 Since the first reports of solid-state hybrid perovskite solar cells in 2012,4 power conversion efficiencies (PCEs) have increased dramatically up to 22.1%.5 Despite the rapid rise in efficiencies of the hybrid lead perovskite such as CH3NH3PbI3 (MAPbI3), their poor long-term stability6,7 and the toxicity of water-soluble lead compounds,8 necessitates the development of alternative lead-free halide perovskite materials with improved moisture tolerance.One solution to instability issues has been proposed in the form of the layered hybrid perovskites, which show less PCE degradation over time than their 3D counterparts.9–12 2D hybrid perovskites, with the formula (RNH3)2(MA)n−1BnI3n+1 (where MA = CH3NH3+), contain large cations which are sandwiched between slabs of perovskite-like sheets. 2D perovskites can be produced if the organic cation, such as CH3(CH2)3NH3+ (BA), and C6H5(CH2)2NH3+ (PEA), is too big to fit in the perovskite cage.13,14 Although 2D hybrid halide perovskites have been known since they were first synthesised by Mitzi et al. in 1994,15 they were not investigated as solar cell absorbers until Smith et al. found the 2D perovskites to be more resistant to moisture than their 3D analogues,9 owing to the hydrophobicity of the organic cation16 and van der Waals interactions between the organic molecules and the surface of the inorganic framework.17,18
Besides enhanced moisture tolerance, 2D perovskites also present other prospective benefits. For example, the inorganic framework provides the potential for high carrier mobilities, whereas the organic moiety can enable intense photoluminescence (PL), owing to the quantum confinement effect.19,20 Compared with the 3D hybrid perovskites, the 2D configuration provides greater flexibility for morphology and electronic structure engineering. This has been exemplified in the L2(BX3)n−1BX4 series (where L = octylammonium, butylammonium; B = Sn, Pb; X = Cl, Br, I), in which choice of alkyl chain length and perovskite-like layer thickness play a crucial role in controlling platelet size and band gap.21 Additionally, environmental concerns can be addressed by replacing Pb with less toxic elements, such as Sn and Ge.22–24 The band gaps of the 2D series generally decrease monotonically with increasing perovskite-like layer thickness, finally tending to that of corresponding 3D perovskite.25,26 In this way, the 2D hybrid perovskites have attracted increasing attention and witnessed a sharp rise in efficiency over the past two years,27 with champion devices (containing (PEA)2(MA)59Pb60I181) showing efficiencies of 15.3%.12
Despite these recent improvements, most devices containing 2D perovskites show efficiencies below 5%, due to the increase in band gap associated with moving from a 3D connected metal-halide framework to one with 2D connectivity.9,10,26,28 Based on the well-known Shockley–Queisser limit,29 a solar absorber should possess a band gap between 1.0 and 1.5 eV (ref. 30) to maximise its efficiency. This limits the applicability of the butylammonium containing layered perovskites, (BA)2(MA)n−1PbnI3n+1, which possess band gaps of 2.43, 2.17 and 2.03 eV for the n = 1, 2, and 3 compositions, respectively.10 Similar to the reduction in band gap seen when moving from MAPbI3 (1.55 eV) to MASnI3 (1.2 eV), the band gaps of the Sn-based butylammonium layered perovskites are smaller than to their Pb analogues.26 As recently demonstrated by Cao et al., the (BA)2(MA)n−1SnnI3n+1 series are semiconductors with band gaps decreasing from 1.83 eV (n = 1), to 1.64 eV (n = 2), and 1.50 eV (n = 3).26 Particularly in the case of the n = 3 composition, these band gaps are closer to the ideal specified by the Shockley–Queisser limit and should enable increased efficiencies. Furthermore, it has been suggested that the Sn-based iodide perovskites possess much lower exciton binding energies than their lead counterparts, due to their larger dielectric constants, and should therefore show reduced open-circuit voltage losses. Thus, the low n tin-based 2D perovskites should possess the best of both worlds, with optimal band gaps and improved moisture stability.
In 2017, the n = 3 and 4 structures of the (BA)2(MA)n−1SnnI3n+1 series were fabricated into heterojunction solar cell devices, using mesoporous TiO2 as an electron-accepting layer.26 Despite growing the 2D perovskites with the sheets aligned perpendicular to the electrodes (as shown to be necessary in highly efficient 2D perovskite devices),10 the devices showed poor efficiencies of 1.94% (n = 3) and 2.53% (n = 4). This was, in part, due to low fill factor and small open-circuit voltages (Voc) of 382 mV (n = 3) and 229 mV (n = 4), well below the optical band gaps of the materials. Importantly, however, the stability of the devices was drastically improved, with 90% of the initial efficiency retained after 1 month, in contrast to comparable MASnI3 films which deteriorated to 0% efficiency in a similar timeframe. Despite poor efficiencies, this series shows promise for the future of lead-free perovskite solar cells, with the authors highlighting a clear path to improve efficiencies, through use of alternative electron contact materials to enable higher Voc.
In this paper, we investigate the optoelectronic properties of a series of Sn containing layered hybrid perovskites, (BA)2(MA)n−1SnnI3n+1 (n = 1, 2 and 3), using relativistic hybrid density functional theory. We systematically assess the relationship between crystal structure and electronic properties, in particular the effect of octahedral distortions. Lastly, evaluation of the thin-film photovoltaic ability of the series, indicates promising applications in the future of lead-free perovskite solar cells.
Computational methodology
First-principles calculations were performed using the Vienna Ab initio Simulation Package (VASP).31–34 The interactions between core and valence electrons were described via the projector augmented-wave (PAW) method.35,36 The plane wave cut-off energy was set to 580 eV, with a Γ-centered 3 × 3 × 1 k-point mesh employed for the unit cells of the n = 1 and n = 3 structures, and a Γ-centered 3 × 3 × 2 used for the unit cell of the n = 2 composition, of which structures are shown in Fig. S1 and the lattice parameters are provided in Table S1 of the ESI.† These parameters were necessary to converge the total energy of each system to within 1 meV per atom.Based on previous studies on the hybrid perovskites, we tested lattice relaxations using two functionals:37–39 the Perdew–Burke–Ernzerhof functional40 (PBE), with dispersion interactions included via Grimme's D3 dispersion correction41 (PBE-D3), and the PBEsol functional,42 a version of PBE revised for solids. Both functionals have been shown to accurately reproduce the structural parameters of layered materials and those containing weak van der Waals' type forces.43,44 During geometry optimisation, the atomic positions, lattice shape and cell volume were allowed to relax, until the forces on each atom totalled less than 0.02 eV Å−1.
In order to obtain an accurate description of the electronic structure of our systems, hybrid density functional theory was employed. Here, we used the Heyd–Scuseria–Ernzerhof (HSE) functional45,46 incorporating 43% Hartree–Fock exact exchange α and 100% of the correlation energy from PBE. This has been shown to reproduce the band gap of MAPbl3,47 and therefore we expect that it will perform well here. To properly account for the relativistic effects present on the heavy elements Sn and I,48–51 all electronic structure calculations explicitly included spin–orbit coupling (SOC). This combination of HSE43 + SOC was used for all band structure, density of states, optical absorption and charge density calculations. The high-frequency dielectric response was calculated from the optical transition matrix elements within the transversal approximation.52,53 The ionic dielectric contribution was calculated using density functional perturbation theory (DFPT),54 using the PBE-D3 functional. Crystal Orbital Hamilton Population (COHP) analysis was performed using the LOBSTER program55,56 based on wavefunctions calculated using HSE43. Due to constraints of the LOBSTER program, spin–orbit effects were not included in the COHP analysis, however, we note that while SOC introduces a slight spin-splitting of the band edges, the orbital nature of the bands is expected to remain unchanged.
Results and discussion
Geometric structure
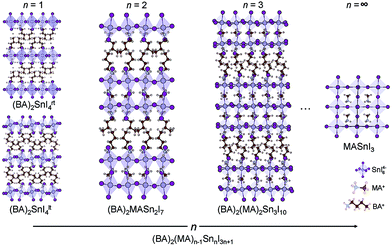
(CH3(CH2)3NH3)2(CH3NH3)n−1SnnI3n+1 (n = 1, 2 and 3) are members of the layered perovskite family adopting the Ruddlesden–Popper type crystal structure, where n is the number of anionic perovskite-like layers, comprising 2D sheets of corner-sharing SnI64− octahedra (Fig. 1).57 The layers are separated from one another by organic butylammonium (BA) cations. The molecule acts to maintain charge neutrality and stabilises the perovskite structure.58 For the n > 1 structures, methylammonium (MA) cations are present in the interstitial site at the centre of the perovskite cage. A larger value of n indicates a thicker perovskite-like component, with n = ∞ equivalent to the 3D perovskite, MASnI3. In this paper, (BA)2SnI4rt (n = 1), (BA)2(MA)Sn2I7 (n = 2) and (BA)2(MA)2Sn3I10 (n = 3) were optimised from the unit cells determined by X-ray diffraction,15,59,60 with the relaxed primitive cells displayed in Fig. S1 of the ESI.† Both a room temperature phase (273 K) and a low temperature phase (128 K) of the n = 1 composition were studied, identified herein as (BA)2SnI4rt and (BA)2SnI4lt, respectively, with the low-temperature phase possessing greater tilting of the octahedra. The low temperature structure was found to be marginally lower in energy by 2.3 meV per atom.Geometry relaxations were trialled using both PBEsol and PBE-D3, with the full results provided in Table S2 of the ESI.† Overall, the PBE-D3 lattice constants showed greater agreement with experiment (Table 1) and, as such, these structures were employed for the rest of this report. We note that the β parameter of the n = 2 structure increased upon lattice relaxation, likely due to the fixed orientations of the organic cations which will show significant flexibility in the room temperature structure. All other lattice parameters showed acceptable agreement with the experimental values.
| Compounds | Functional | a | b | c | α | β | γ |
|---|---|---|---|---|---|---|---|
| (BA)2SnI4rt | PBE-D3 | 8.497 | 8.724 | 28.034 | 90.0 | 90.0 | 90.0 |
| Ref. 59 | 8.591 | 8.814 | 27.644 | 90.0 | 90.0 | 90.0 | |
| (BA)2SnI4lt | PBE-D3 | 8.410 | 8.911 | 26.074 | 90.0 | 90.0 | 90.0 |
| Ref. 59 | 8.408 | 8.932 | 26.023 | 90.0 | 90.0 | 90.0 | |
| (BA)2(MA)Sn2I7 | PBE-D3 | 39.458 | 8.946 | 8.479 | 90.0 | 95.1 | 90.0 |
| Ref. 60 | 39.497 | 8.858 | 8.776 | 90.0 | 90.0 | 90.0 | |
| (BA)2(MA)2Sn3I10 | PBE-D3 | 8.551 | 50.184 | 9.085 | 89.4 | 90.9 | 92.0 |
| Ref. 15 | 8.795 | 51.921 | 8.858 | 90.0 | 90.0 | 90.0 |
Electronic properties
The fundamental band gaps of the series, calculated using HSE43 + SOC, are listed in Table 2. In all cases, the band gaps are larger than that of MASnI3 (1.3 eV).22 As expected, the band gaps decrease monotonically as the thickness of the perovskite layer increases (Fig. 1),24,61,62 from 1.85 eV (n = 1), to 1.50 eV (n = 2), and 1.38 eV in the n = 3 case. These are in good agreement with ultraviolet-visible spectroscopic measurements, which show band gaps of 1.83, 1.64 eV, and 1.50 eV for the n = 1, 2, and 3 structures, respectively.26| Compounds | E g | ∠SnISn | ∠‖SnISn | ∠⊥SnISn | m ‖h | m ‖e | ε ‖r | ε ⊥r | SLMEa |
|---|---|---|---|---|---|---|---|---|---|
| a Thickness: 0.5 μm. | |||||||||
| (BA)2SnI4rt | 1.85 | 153.5 | 26.4 | 2.3 | 0.13 | 0.15 | 21.24 | 4.36 | 19.01 |
| (BA)2SnI4lt | 2.13 | 149.6 | 21.3 | 22.3 | 0.20 | 0.18 | 31.87 | 5.19 | 15.24 |
| (BA)2(MA)Sn2I7 | 1.50 | 168.3 | 5.3 | 7.8 | 0.13 | 0.14 | 34.05 | 11.71 | 22.64 |
| (BA)2(MA)2Sn3I10 | 1.38 | 168.2 | 7.3 | 9.1 | 0.13 | 0.13 | 47.99 | 9.77 | 24.64 |
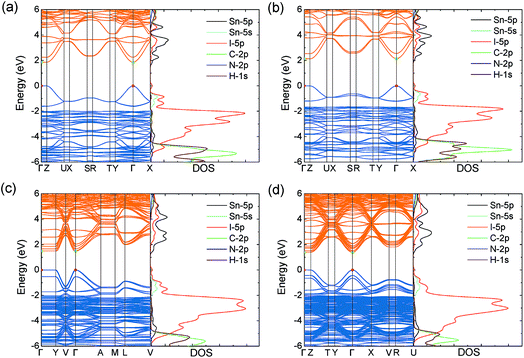
Similar to MASnI3,49 the upper valence band of the series is determined by Sn 5s and I 5p anti-bonding orbitals, with the lower conduction band composed entirely of Sn 5p anti-bonding orbitals (Fig. 2), both of which give rise to excellent band dispersion. The antibonding character of these states is demonstrated by the Crystal Orbital Hamilton Population (COHP) analysis provided in Fig. S2 of the ESI.† Because the states of the organic cations are several eV away from the band edges, they will not play a role in determining the electron and hole transport properties. The HSE43 + SOC calculated band structures for the series are plotted in Fig. 2. The results indicate that all systems possess direct fundamental band gaps with the valence band minimum (VBM) and conduction band maximum (CBM) situated at the Γ point (0.0, 0.0, 0.0).
Both the VBM and CBM are dispersive along the directions parallel to the perovskite-like layers (Y–Γ and Γ–X), while they are flat in the perpendicular direction (Γ–Z), due to the 2D connectivity of the tin iodide octahedra. As a result, the calculated effective masses are nearly infinite in the perpendicular direction, indicating carriers will be immobile across the layers (Table 2). Accordingly, any devices containing these systems should possess [SnnI3n+1](1+n)− slabs that are oriented perpendicular to the device contacts, allowing for efficient extraction of charge carriers to the electrodes. This has recently been demonstrated experimentally for the (BA)2(MA)n−1SnnI3n+1 series, in which judicial choice of solvent enables control over the orientation of the perovskite-like layers.26
Owing to the dispersive VBM and CBM, the series display light hole and electron effective masses in the directions parallel to the 2D sheets (in all cases below 0.2m0). Moving across the series, the carrier effective masses decrease as the thickness of the inorganic layer increases. In particular, the n = 3 composition possesses light hole and electron effective masses of 0.13m0 and 0.13m0, respectively, smaller than those of MAPbI3 (0.25m0 and 0.19m0) and comparable to the effective masses of MASnI3 (0.13m0 and 0.28m0) calculated by GW + SOC.48 In general, the series shows slightly larger masses than their lead analogues, such as (BA)2PbI4 (0.14m0 and 0.08m0), (BA)2(MA)2Pb3I10 (0.14m0 and 0.10m0), (BA)2(MA)3Pb4I13 (0.15m0 and 0.09m0), as calculated by Stoumpos et al.25 We note that the calculations performed by Stoumpos et al. did not include the effects of spin–orbit coupling, and may therefore not accurately represent the true properties of the systems.
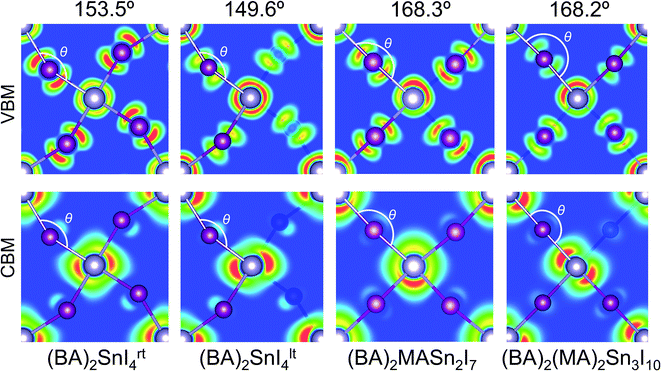
Previous reports have indicated the Sn–I–Sn bond angle (∠SnIsn) as a primary factor in the controlling electronic properties of lead and tin based layered perovskites.24,61,62 This bond angle quantifies the degree of distortion in the SnI64− octahedra, with a value of 180° indicating the ideal (undistorted) structure. This distortion can be further broken down into its in-plane (∠‖SnISn) and out-of-plane (∠⊥SnISn) components. Analysis of the distortion angle provides an explanation for the discrepancy in band gap between room temperature and low temperature n = 1 structures (Table 2). The greater distortion in the Sn–I–Sn bond angle of (BA)2SnI4lt (149.6°) gives rise to an increased band gap of 2.13 eV, compared with a band gap of 1.85 eV for the room temperature structure (153.5°). The Sn–I–Sn angle, when decomposed into it's out-of-plane and in-plane contributions, indicates the in-plane distortion remains similar (26.4° vs. 21.3°), whereas the out-of-plane distortion is significantly greater in the tilted structure (22.3° vs. 2.3°), and is therefore likely responsible for the variation in band gap. We note, that in general our results contrast previous reports, which suggest the in-plane distortion plays a greater role in tuning the band gap.61,62 In reality, as both distortions occur simultaneously, the effect of the distortions will be cooperative and should be considered at the same time, as quantified by the overall Sn–I–Sn bond angle. For the n = 2 and 3 structures, the tilting angles were found to be close to the ideal (168.3° and 168.2°), indicating relatively little structural distortion.
The charge density isosurfaces shown in Fig. 3, provide an explanation for the effect of Sn–I–Sn bond angle on electronic properties. Due to the structural distortion, the in-plane I atoms are displaced such that they do not sit directly between two adjacent Sn atoms. As demonstrated in the inorganic perovskite, CsPbI3,61,62 greater distortion results in a reduction of the in-plane orbital overlap of the states that comprise the upper valence band (Sn 5s and I 5p), producing larger hole effective masses and a narrower valence band width. Likewise, a similar effect is found on the lower conduction band overlap (composed of Sn 5p and a small contribution from the I 5p), which increases its band width and results in greater electron effective masses. For example, within the n = 1 structures, the greater distortion of (BA)2SnI4lt (149.6°) compared to (BA)2SnI4rt (153.5°), results in a wider band gap (2.13 eV), larger effective masses of electrons (0.20m0) and holes (0.18m0), and reduced valence (0.95 eV) and conduction band widths (1.53 eV). Further analysis of the charge density isosurfaces in the two n = 1 structures (Fig. S3 of the ESI†), indicates the conduction band minima are derived mainly of Sn 5px and py orbitals, with the pz orbital showing very little contribution. For this reason, the out-of-plane distortion will have a reduced impact on the electronic properties of the conduction band, compared with the in-plane distortion, explaining the limited variation in electron effective masses and conduction band widths between the two structures. For the n = 2, and 3 structures, the minimal distortion further produces optimal optoelectronic properties, such as small band gaps very light hole and electron effective masses.
Optical properties
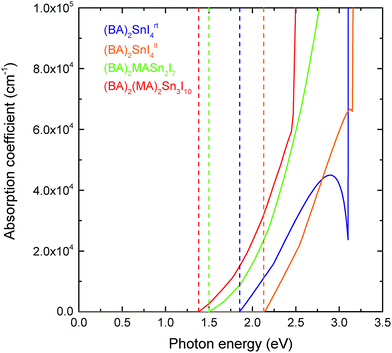
In comparison to the 3D hybrid perovskites, the unique layered configuration introduces a directional dependence into the dielectric constants and optical response. 2D perovskites can be regarded as quantum-well-like structures, of which the inorganic sheets (“wells”) are more polarisable, and the organic layers (“barriers”) are less polarisable.63,64 Previous computational studies have shown that in the 2D hybrid perovskites, the dielectric constant of the inorganic component is significantly greater than that of the organic layer.65,66 Since the bulk dielectric response calculated here corresponds to an average over both the inorganic and organic components, those compounds with thicker inorganic layers should possess greater dielectric constants. This is in agreement with our results, which show that both the in-plane (ε‖r) and out-of-plane (ε⊥r) dielectric constants increase as the thickness of the perovskite-like layer increases. For the n = 1 (BA)2SnI4rt structure, the in-plane and out-of-plane dielectric constants are 21.24 and 4.36, respectively, which increase to 34.05 and 11.71 for the n = 2 structure, and 47.99 and 9.77 in the n = 3 case. As n decreases, the negative charge arising from the perovskite-like surface is distributed over a decreasing number of Sn and I ions. This has the effect of making these ions less positive, in turn reducing their polarisability and thus their ability to screen charge, as evidenced by the reduction in their Born effective charge (provided in Table S3 of the ESI†). In general, the dielectric constants for the direction perpendicular to the perovskite sheets are much smaller than those in the parallel directions. Again, the Sn–I–Sn bond angle plays an important role, with the low temperature, more distorted structure ((BA)2SnI4lt) actually showing larger in-plane and out-of-plane dielectric constants (31.87 and 5.19, respectively) than the room temperature compound.As discussed in the introduction, one of the advantages of the tin layered perovskites over their lead analogues is that their fundamental band gaps are closer to the optimum value for a single junction solar cell.30 The optical response for the series, calculated using HSE43 + SOC, is provided in Fig. 4. Similar to other layered perovskites,11,12,25 an increase in the perovskite-like layer thickness causes a red shifting of the absorption edge. In all cases, the optical absorption edges of the (BA)2(MA)n−1SnnI3n+1 (n = 1, 2 and 3) series are located at the fundamental band gaps, indicating that the fundamental band gap transitions are symmetry allowed. All four perovskites studied exhibit strong optical absorption, with the absorption coefficient reaching 105 cm−1 within ∼1 eV of the band edge. The strength of optical absorption is dependent on the thickness of the inorganic component—as the number of layers increases, the optical absorption gets stronger. This is to be expected as the organic cations do not contribute to the optical response until larger excitation energies.
In the Shockley–Queisser limit,29 the efficiency of an absorber is dependant solely on its band gap. In practice, however, strong visible light absorption as well as a fundamental allowed band gap transition are also critical for achieving high efficiency cells. In a real solar cell, the maximum efficiency is also determined by the thickness of the absorber layer. After taking all the above factors into consideration, the maximum photovoltaic efficiency of an ideal absorber thin film can be simulated using the spectroscopic limited maximum efficiency (SLME) metric proposed by Yu and Zunger.67 The SLME metric improves on the Shockley–Queisser limit in a number of ways: firstly, the non-radiative recombination rate is approximated, based on the difference between the lowest allowed optical transition and the fundamental band gap; secondly, the frequency dependant absorption coefficient of the material is taken into account; lastly, the thin-film thickness is also considered. The full details of how the SLME is calculated are provided in the ESI.†
In order to evaluate the photovoltaic performance of these 2D perovskites, the SLMEs, computed based on a thin film thickness of 0.5 μm, are listed in Table 2. The n = 3 composition possesses the highest efficiency (24.6%) as expected based on it's high optical absorption coefficient and favourable band gap (1.38 eV), which is close to the optimal value based on the Shockley–Queisser limit. The predicted SLME values are significantly higher than efficiencies of the devices produced by Cao et al.,10 highlighting the potential of further device engineering. The high SLME of (BA)2(MA)2Sn3I10 is comparable to that of many state-of-art solar cell absorbers, such as CdTe (24.85%) and CuZnSnS (25.71%), and even greater than that of MAPbI3 (22.1%), further confirming its potential as a lead-free replacement to the 3D hybrid perovskites.68
Conclusion
In summary, we have shown that the layered lead-free perovskites (BA)2(MA)n−1SnnI3n+1 (BA = CH3(CH2)3NH3+, MA = CH3NH3+, n = 1, 2 and 3) exhibit intrinsic properties that are well suited for solar cell applications, including band gaps close to the ideal indicated by the Shockley–Queisser limit and strong optical absorption. Furthermore, both electrons and holes show small effective masses in the directions parallel to the perovskite-like sheets. We have further elucidated the role that structural distortions, in the form of octahedral tilting, play in determining the optoelectronic properties of the series. Impressively, the champion absorber, (BA)2(MA)2Sn3I10 (n = 3), displays a high spectroscopic limited maximum efficiency greater than 24%. Based on these properties, the structures where n ≤ 2, are promising candidates for top cells in tandem devices, whereas the n = 3 composition is expected to perform well in a heterojunction solar cell in its own right. Despite the low power conversion efficiencies previously demonstrated by Cao et al.,26 our results indicate a significant scope for improvement and suggest further device engineering and optimisation may be fruitful.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work made use of the ARCHER UK National Supercomputing Service (http://www.archer.ac.uk), via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202). DOS acknowledges support from the EPSRC (EP/N01572X/1). DOS acknowledges membership of the Materials Design Network. CN acknowledges the financial support from the National Natural Science Foundation of China (Grant No. 21773182). AMG acknowledges Diamond Light Source for the co-sponsorship of a studentship on the EPSRC Centre for Doctoral Training in Molecular Modelling and Materials Science (EP/L015862/1). ZW acknowledges the China Scholarship Council (CSC) for supporting a visit to University College London.References
- J. Chow, R. J. Kopp and P. R. Portney, Energy resources and global development, Science, 2003, 302, 1528–1531 CrossRef PubMed.
- Q. Schiermeier, J. Tollefson, T. Scully, A. Witze and O. Morton, Energy alternatives: Electricity without carbon, Nature, 2008, 454, 816–823 CrossRef CAS PubMed.
- A. Polman, M. Knight, E. C. Garnett, B. Ehrler and W. C. Sinke, Photovoltaic materials: Present efficiencies and future challenges, Science, 2016, 352, aad4424 CrossRef PubMed.
- H.-S. Kim, C.-R. Lee, J.-H. Im, K.-B. Lee, T. Moehl, A. Marchioro, S.-J. Moon, R. Humphry-Baker, J.-H. Yum, J. E. Moser, M. Grätzel and N.-G. Park, Lead iodide perovskite sensitized all-solid-state submicron thin film mesoscopic solar cell with efficiency exceeding 9%, Sci. Rep., 2012, 2, 591 CrossRef PubMed.
- W. S. Yang, B.-W. Park, E. H. Jung, N. J. Jeon, Y. C. Kim, D. U. Lee, S. S. Shin, J. Seo, E. K. Kim, J. H. Noh and S. I. Seok, Iodide management in formamidinium-lead-halide-based perovskite layers for efficient solar cells, Science, 2017, 356, 1376–1379 CrossRef CAS PubMed.
- S. Ahmad, P. K. Kanaujia, H. J. Beeson, A. Abate, F. Deschler, D. Credgington, U. Steiner, G. V. Prakash and J. J. Baumberg, Strong Photocurrent from Two-Dimensional Excitons in Solution-processed Stacked Perovskite Semiconductor Sheets, ACS Appl. Mater. Interfaces, 2015, 7, 25227–25236 CAS.
- G. Nagabhushana, R. Shivaramaiah and A. Navrotsky, Direct calorimetric verification of thermodynamic instability of lead halide hybrid perovskites, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 7717–7721 CrossRef CAS PubMed.
- G. Niu, X. Guo and L. Wang, Review of recent progress in chemical stability of perovskite solar cells, J. Mater. Chem. A, 2015, 3, 8970–8980 CAS.
- I. C. Smith, E. T. Hoke, D. Solis-Ibarra, M. D. McGehee and H. I. Karunadasa, A Layered Hybrid Perovskite Solar-Cell Absorber with Enhanced Moisture Stability, Angew. Chem., Int. Ed., 2014, 126, 11414–11417 CrossRef.
- D. H. Cao, C. C. Stoumpos, O. K. Farha, J. T. Hupp and M. G. Kanatzidis, 2D homologous perovskites as light-absorbing materials for solar cell applications, J. Am. Chem. Soc., 2015, 137, 7843–7850 CrossRef CAS PubMed.
- H. Tsai, W. Nie, J.-C. Blancon, C. C. Stoumpos, R. Asadpour, B. Harutyunyan, A. J. Neukirch, R. Verduzco, J. J. Crochet, S. Tretiak, L. Pedesseau, J. Even, M. A. Alam, G. Gupta, J. Lou, P. M. Ajayan, M. J. Bedzyk, M. G. Kanatzidis and A. D. Mohite, High-efficiency two-dimensional Ruddlesden-Popper perovskite solar cells, Nature, 2016, 536, 312–316 CrossRef CAS PubMed.
- L. N. Quan, M. Yuan, R. Comin, O. Voznyy, E. M. Beauregard, S. Hoogland, A. Buin, A. R. Kirmani, K. Zhao, A. Amassian, D. H. Kim and E. H. Sargent, Ligand-stabilized reduced-dimensionality perovskites, J. Am. Chem. Soc., 2016, 138, 2649–2655 CrossRef CAS PubMed.
- G. Kieslich, S. Sun and A. K. Cheetham, An extended tolerance factor approach for organic–inorganic perovskites, Chem. Sci., 2015, 6, 3430–3433 RSC.
- W. Travis, E. Glover, H. Bronstein, D. Scanlon and R. Palgrave, On the application of the tolerance factor to inorganic and hybrid halide perovskites: a revised system, Chem. Sci., 2016, 7, 4548–4556 RSC.
- D. B. Mitzi, C. Feild, W. Harrison and A. Guloy, Conducting tin halides with a layered organic-based perovskite structure, Nature, 1994, 369, 467–469 CrossRef CAS.
- D. Bi, P. Gao, R. Scopelliti, E. Oveisi, J. Luo, M. Grätzel, A. Hagfeldt and M. K. Nazeeruddin, High-Performance Perovskite Solar Cells with Enhanced Environmental Stability Based on Amphiphile-Modified CH3NH3PbI3, Adv. Mater., 2016, 28, 2910–2915 CrossRef CAS PubMed.
- D. B. Mitzi, K. Chondroudis and C. R. Kagan, Organic–inorganic electronics, IBM J. Res. Dev., 2001, 45, 29–45 CrossRef CAS.
- W. Jiang, J. Ying, W. Zhou, K. Shen, X. Liu, X. Gao, F. Guo, Y. Gao and T. Yang, A new layered nano hybrid perovskite film with enhanced resistance to moisture-induced degradation, Chem. Phys. Lett., 2016, 658, 71–75 CrossRef CAS.
- T. Hattori, T. Taira, M. Era, T. Tsutsui and S. Saito, Highly efficient electroluminescence from a heterostructure device combined with emissive layered-perovskite and an electron-transporting organic compound, Chem. Phys. Lett., 1996, 254, 103–108 CrossRef CAS.
- G. V. Prakash, Naturally self-assembled nanosystems and their templated structures for photonic applications, J. Nanopart., 2013, 2013, 2013 Search PubMed.
- M. C. Weidman, M. Seitz, S. D. Stranks and W. A. Tisdale, Highly tunable colloidal perovskite nanoplatelets through variable cation, metal, and halide composition, ACS Nano, 2016, 8, 7830–7839 CrossRef PubMed.
- F. Hao, C. C. Stoumpos, D. H. Cao, R. P. Chang and M. G. Kanatzidis, Lead-free solid-state organic–inorganic halide perovskite solar cells, Nat. Photonics, 2014, 8, 489–494 CrossRef CAS.
- N. K. Noel, S. D. Stranks, A. Abate, C. Wehrenfennig, S. Guarnera, A.-A. Haghighirad, A. Sadhanala, G. E. Eperon, S. K. Pathak, M. B. Johnston, A. Petrozza, L. M. Herz and H. J. Snaith, Lead-free organic–inorganic tin halide perovskites for photovoltaic applications, Energy Environ. Sci., 2014, 7, 3061–3068 CAS.
- C. C. Stoumpos, L. Frazer, D. J. Clark, Y. S. Kim, S. H. Rhim, A. J. Freeman, J. B. Ketterson, J. I. Jang and M. G. Kanatzidis, Hybrid germanium iodide perovskite semiconductors: active lone pairs, structural distortions, direct and indirect energy gaps, and strong nonlinear optical properties, J. Am. Chem. Soc., 2015, 137, 6804–6819 CrossRef CAS PubMed.
- C. C. Stoumpos, D. H. Cao, D. J. Clark, J. Young, J. M. Rondinelli, J. I. Jang, J. T. Hupp and M. G. Kanatzidis, Ruddlesden–Popper hybrid lead iodide perovskite 2D homologous semiconductors, Chem. Mater., 2016, 28, 2852–2867 CrossRef CAS.
- D. H. Cao, C. C. Stoumpos, T. Yokoyama, J. L. Logsdon, T.-B. Song, O. K. Farha, M. R. Wasielewski, J. T. Hupp and M. G. Kanatzidis, Thin Films and Solar Cells Based on Semiconducting Two-Dimensional Ruddlesden–Popper (CH3(CH2)3NH3)2(CH3NH3)n−1SnnI3n+1 Perovskites, ACS Energy Lett., 2017, 2, 982–990 CrossRef.
- A. M. Ganose, C. N. Savory and D. O. Scanlon, Beyond Methylammonium Lead Iodide: Prospects for the Emergent Field of ns2 Containing Solar Absorbers, Chem. Commun., 2017, 53, 20–44 RSC.
- S. J. Lee, S. S. Shin, Y. C. Kim, D. Kim, T. K. Ahn, J. H. Noh, J. Seo and S. I. Seok, Fabrication of efficient formamidinium tin iodide perovskite solar cells through SnF2–pyrazine complex, J. Am. Chem. Soc., 2016, 138, 3974–3977 CrossRef PubMed.
- W. Shockley and H. J. Queisser, Detailed balance limit of efficiency of p–n junction solar cells, J. Appl. Phys., 1961, 32, 510–519 CrossRef CAS.
- L. Yu, R. S. Kokenyesi, D. A. Keszler and A. Zunger, Inverse Design of High Absorption Thin-Film Photovoltaic Materials, Adv. Energy Mater., 2013, 3, 43–48 CrossRef CAS.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS.
- G. Kresse and J. Hafner, Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- F. Brivio, A. B. Walker and A. Walsh, Structural and Electronic Properties of Hybrid Perovskites for High-Efficiency Thin-Film Photovoltaics from First-Principles, APL Mater., 2013, 1, 042111 CrossRef.
- K. T. Butler, J. M. Frost and A. Walsh, Band alignment of the hybrid halide perovskites CH3NH3PbCl3, CH3NH3PbBr3 and CH3NH3PbI3, Mater. Horiz., 2015, 2, 228–231 RSC.
- C. N. Savory, R. G. Palgrave, H. Bronstein and D. O. Scanlon, Spatial Electron-hole Separation in a One Dimensional Hybrid Organic–Inorganic Lead Iodide, Sci. Rep., 2016, 6, 20626 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- S. Grimme, Accurate description of van der Waals complexes by density functional theory including empirical corrections, J. Comput. Chem., 2004, 25, 1463–1473 CrossRef CAS PubMed.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Restoring the density-gradient expansion for exchange in solids and surfaces, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- A. M. Ganose, K. T. Butler, A. Walsh and D. O. Scanlon, Relativistic electronic structure and band alignment of BiSI and BiSeI: candidate photovoltaic materials, J. Mater. Chem. A, 2016, 4, 2060–2068 CAS.
- A. M. Ganose, C. N. Savory and D. O. Scanlon, Electronic and defect properties of (CH3NH3)2Pb(SCN)2I2 analogues for photovoltaic applications, J. Mater. Chem. A, 2017, 5, 7845–7853 CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid functionals based on a screened Coulomb potential, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, Erratum: “Hybrid functionals based on a screened Coulomb potential” [J. Chem. Phys. 118, 8207 (2003)], J. Chem. Phys., 2006, 124, 219906 CrossRef.
- M. H. Du, Efficient carrier transport in halide perovskites: theoretical perspectives, J. Mater. Chem. A, 2014, 2, 9091–9098 CAS.
- P. Umari, E. Mosconi and F. De Angelis, Relativistic GW calculations on CH3NH3PbI3 and CH3NH3SnI3 perovskites for solar cell applications, Sci. Rep., 2014, 4, 4467 CrossRef PubMed.
- C. Bernal and K. Yang, First-principles hybrid functional study of the organic–inorganic perovskites CH3NH3SnBr3 and CH3NH3SnI3, J. Phys. Chem. C, 2014, 118, 24383–24388 CAS.
- J. Im, C. C. Stoumpos, H. Jin, A. J. Freeman and M. G. Kanatzidis, Antagonism between Spin–Orbit Coupling and Steric Effects Causes Anomalous Band Gap Evolution in the Perovskite Photovoltaic Materials CH3NH3Sn1−xPbxI3, J. Phys. Chem. Lett., 2015, 6, 3503–3509 CrossRef CAS PubMed.
- J. Even, L. Pedesseau, J.-M. Jancu and C. Katan, DFT and k·p modelling of the phase transitions of lead and tin halide perovskites for photovoltaic cells, Phys. Status Solidi RRL, 2014, 8, 31–35 CrossRef CAS.
- P. E. Blöchl, O. Jepsen and O. K. Andersen, Improved tetrahedron method for Brillouin-zone integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223 CrossRef.
- M. Gajdoš, K. Hummer, G. Kresse, J. Furthmüller and F. Bechstedt, Linear Optical Properties in the Projector-Augmented Wave Methodology, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 045112 CrossRef.
- S. Baroni, S. De Gironcoli, A. Dal Corso and P. Giannozzi, Phonons and related crystal properties from density-functional perturbation theory, Rev. Mod. Phys., 2001, 73, 515 CrossRef CAS.
- R. Dronskowski and P. E. Bloechl, Crystal orbital Hamilton populations (COHP): energy-resolved visualization of chemical bonding in solids based on density-functional calculations, J. Phys. Chem., 1993, 97, 8617–8624 CrossRef CAS.
- S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, Analytic projection from plane-wave and PAW wavefunctions and application to chemical-bonding analysis in solids, J. Comput. Chem., 2013, 34, 2557–2567 CrossRef CAS PubMed.
- J. Calabrese, N. Jones, R. Harlow, N. Herron, D. Thorn and Y. Wang, Preparation and characterization of layered lead halide compounds, J. Am. Chem. Soc., 1991, 113, 2328–2330 CrossRef CAS.
- C. Motta, F. El-Mellouhi, S. Kais, N. Tabet, F. Alharbi and S. Sanvito, Revealing the role of organic cations in hybrid halide perovskite CH3NH3PbI3, Nat. Commun., 2015, 6, 7026 CrossRef CAS PubMed.
- Y. Takahashi, R. Obara, K. Nakagawa, M. Nakano, J.-y. Tokita and T. Inabe, Tunable Charge Transport in Soluble Organic–Inorganic Hybrid Semiconductors, Chem. Mater., 2007, 19, 6312–6316 CrossRef CAS.
- C. C. Stoumpos, L. Mao, C. D. Malliakas and M. G. Kanatzidis, Structure-Band Gap Relationships in Hexagonal Polytypes and Low-Dimensional Structures of Hybrid Tin Iodide Perovskites, Inorg. Chem., 2017, 56, 56–73 CrossRef CAS PubMed.
- J. L. Knutson, J. D. Martin and D. B. Mitzi, Tuning the band gap in hybrid tin iodide perovskite semiconductors using structural templating, Inorg. Chem., 2005, 44, 4699–4705 CrossRef CAS PubMed.
- Z. Xiao, W. Meng, J. Wang, D. B. Mitzi and Y. Yan, Searching for promising new perovskite-based photovoltaic absorbers: the importance of electronic dimensionality, Mater. Horiz., 2017, 4, 206–216 RSC.
- T. Ishihara, Optical properties of PbI-based perovskite structures, J. Lumin., 1994, 60, 269–274 CrossRef.
- J. Even, L. Pedesseau and C. Katan, Understanding quantum confinement of charge carriers in layered 2D hybrid perovskites, ChemPhysChem, 2014, 15, 3733–3741 CrossRef CAS PubMed.
- D. Sapori, M. Kepenekian, L. Pedesseau, C. Katan and J. Even, Quantum confinement and dielectric profiles of colloidal nanoplatelets of halide inorganic and hybrid organic–inorganic perovskites, Nanoscale, 2016, 8, 6369–6378 RSC.
- M. D. Smith, L. Pedesseau, M. Kepenekian, I. C. Smith, C. Katan, J. Even and H. I. Karunadasa, Decreasing the electronic confinement in layered perovskites through intercalation, Chem. Sci., 2017, 8, 1960–1968 RSC.
- L. Yu and A. Zunger, Identification of potential photovoltaic absorbers based on first-principles spectroscopic screening of materials, Phys. Rev. Lett., 2012, 108, 068701 CrossRef PubMed.
- Unpublished results provided by internal correspondence with C. N. Savory.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ta00751a |
| This journal is © The Royal Society of Chemistry 2018 |