Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Influence of water intercalation and hydration on chemical decomposition and ion transport in methylammonium lead halide perovskites
Un-Gi
Jong
ab,
Chol-Jun
Yu
 *a,
Gum-Chol
Ri
a,
Andrew P.
McMahon
d,
Nicholas M.
Harrison
e,
Piers R. F.
Barnes
d and
Aron
Walsh
*a,
Gum-Chol
Ri
a,
Andrew P.
McMahon
d,
Nicholas M.
Harrison
e,
Piers R. F.
Barnes
d and
Aron
Walsh
 *c
*c
aDepartment of Computational Materials Design, Faculty of Materials Science, Kim Il Sung University, Ryongnam-Dong, Taesong District, Pyongyang, Democratic People's Republic of Korea. E-mail: ryongnam14@yahoo.com
bNatural Science Centre, Kim Il Sung University, Ryongnam-Dong, Taesong District, Pyongyang, Democratic People's Republic of Korea
cDepartment of Materials, Imperial College London, London SW7 2AZ, UK. E-mail: a.walsh@imperial.ac.uk
dDepartment of Physics, Imperial College London, London SW7 2AZ, UK
eDepartment of Chemistry, Imperial College London, London SW7 2AZ, UK
First published on 5th December 2017
Abstract
The application of methylammonium (MA) lead halide perovskites, CH3NH3PbX3 (X = I, Br, Cl), in perovskite solar cells has made great recent progress in performance efficiency during recent years. However, the rapid decomposition of these materials in humid environments hinders outdoor application, and thus, a comprehensive understanding of the degradation mechanism is required. We investigate the effect of water intercalation and hydration of the decomposition and ion migration of CH3NH3PbX3 using first-principles calculations. We find that water interacts with PbX6 and MA through hydrogen bonding, and the former interaction increases gradually, while the latter hardly changes when going from X = I to Br and to Cl. Thermodynamic calculations indicate that water exothermically intercalates into the perovskite, and suggest that the water intercalated and monohydrated compounds are stable with respect to decomposition. More importantly, the water intercalation reduces the activation energies for vacancy-mediated ion migration, which become higher going from X = I to Br and to Cl. Our work indicates that hydration of halide perovskites must be avoided to prevent the degradation of solar cells upon moisture exposure.
1 Introduction
Perovskite solar cells (PSCs) using methylammonium lead halide perovskites MAPbX3 (MA = methylammonium cation CH3NH3+; X = halogen anion I−, Br− or Cl−) as light harvesters have opened up a new stage in the field of photovoltaics. The rapid rise of power conversion efficiency of PSCs from the initial 3.81% reported by Kojima et al. in 2009 (ref. 1) to over 20% (ref. 2 and 3) within a few years is quite remarkable, as compared with other types of solar cells.4–6 Moreover, much low cost of cell fabrication by chemical methods and much abundance of raw materials have attracted great attention, inspiring people with hope that solar power will become competitive with fossil fuels in the electricity market in the near future. In spite of a great advance in research and development of PSCs during the past years, there still remain some obstacles to prevent commercialization of PSCs, such as toxicity of lead7 and mostly poor material stability of these halide perovskites.8–12First-principles calculations revealed that MAPbI3, the most widely used hybrid perovskite halide in PSCs, may be decomposed exothermally13 and such intrinsic instability can be cured by mixing halogen ions.14,15 On the other hand, moisture has been reported to play a critical role as an extrinsic factor in the degradation of PSC performance.16 Although controlled humidity conditions or a small amount of H2O during processing has positive effects on PSC performance such as enhancement of the reconstruction in perovskite film formation and triggering nucleation and crystallization of perovskite phase,17–19 H2O molecule is known to damage the integrity of perovskite films. Some researchers asserted that MAPbI3 may readily hydrolyze in the presence of water due to deprotonation of CH3NH3+ by H2O, resulting in degradation products such as CH3NH2, HI and PbI2.8,20,21 In contrast different degradation reactions in perovskite films under humidity condition have been reported. Huang et al.22 focused on the interaction between H2O and MAPbI3 and suggested that degradation of MAPbI3 under ambient condition may produce PbCO3 and α-PbO rather than PbI2.
Some reports found that the formation of monohydrated CH3NH3PbI3·H2O or dehydrated (CH3NH3)4PbI6·2H2O intermediate phase is the initial step in the perovskite decomposition process under 80% humidity exposure.23–26 It was found subsequently that these intermediate phases are unstable in ambient condition, so that further decomposition into the final products could occur.27–32 As a consequence, the decomposition of MAPbI3 in humid air is a rather complicated process and their reaction processes or mechanisms are in an active controversy. To unveil the mechanism of MAPbI3 decomposition upon humidity exposure, theoretical simulations based on the density functional theory (DFT) have been performed, focused on H2O adsorption on MAPbI3 surfaces.33–36 However, comprehensive understanding of water-assisted decomposition of MAPbI3 is not yet fully established, and is urgent to facilitate materials engineering for enhanced material stability.
In this work, we investigate the influence of water intercalation and hydration on the decomposition of MAPbI3 (X = I, Br, Cl) by performing first-principles calculations. The crystalline and atomistic structures of water intercalated phases, we denote as MAPbI3_H2O, and monohydrated phases MAPbX3·H2O are explored carefully. These phases can be regarded as the intermediates of the process of water-assisted decomposition of MAPbX3. The intercalation energies of a water molecule into the pseudo-cubic phases and the decomposition energies of the water intercalated and monohydrated phases into PbX2, CH3NH3X and H2O are calculated to draw a meaningful conclusions about the stability. Finally we consider vacancy-mediated diffusion of an X− anion, MA+ cation, and H2O molecule in pristine, water intercalated and monohydrated phases, since such migrations seem to give important implication of the material stability.37–41 Pb2+ migration is excluded due to high formation energy of the Pb vacancy, VPb. Our research provides an atomistic understanding of the interaction of water with halide perovskites, and indicates that hydration must be avoided to prevent the degradation upon exposure to moisture.
2 Computational methods
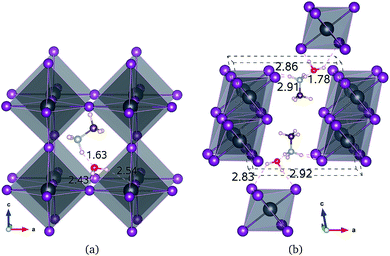
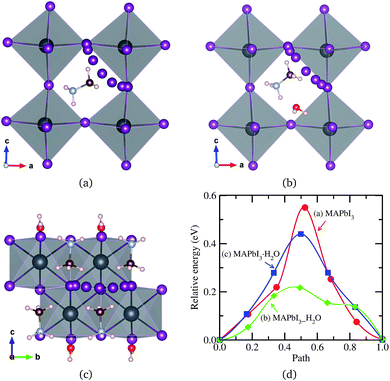
All of the primary DFT calculations were carried out using the pseudopotential plane wave method as implemented in Quantum-ESPRESSO package.42 We used the ultrasoft pseudopotentials provided in the package,† where the valence electronic configurations of atoms are H-1s1, C-2s22p3, N-2s22p3, Cl-3s2p5, Br-4s2p5, I-5s25p5, and Pb-5d106s26p2. The exchange–correlation interaction between the valence electrons was estimated using the Perdew–Burke–Ernzerhof (PBE)43 form within the generalized gradient approximation, which is augmented by dispersive van der Waals interaction (vdW-DF-OB86), already shown to be important for calculations of perovskite halides.44,45 The structures of MAPbX3 and water intercalated phases were assumed to be pseudo-cubic. Unit cells containing one formula unit (f.u.) for these phases and two formula units for monohydrated phase were used for structural optimization and decomposition energetics. For diffusion process, (2 × 2 × 2) supercells for pseudo-cubic phase and (2 × 2 × 1) supercells for monohydrated phases, including 120 and 96 atoms, were used. The cutoff energy for plane-wave basis set is as high as 40 Ry and k-points are (2 × 2 × 2) with Monkhorst–Pack method, which guarantee the total energy accuracy as 5 meV per unit cell. Atomic positions were fully relaxed until the forces converge to 5 × 10−5 Ry per Bohr. The activation energies for migrations were calculated using the climbing image nudged elastic band (NEB) method.46The structural optimizations of pseudo-cubic MAPbX3 phases produced lattice constants of 6.330, 5.949, and 5.682 Å for X = I, Br, and Cl, which are in good agreement with the experimental values47 within 1% relative errors. A water molecule was put into the interstitial space of these optimized cubic phases, which were re-optimized. The supercell shape becomes triclinic following optimization. We have also performed optimization of the monohydrated phases MAPbX3·H2O with monoclinic crystalline lattice and experimentally identified atomic positions.24,26,48,49 For the case of MAPbI3·H2O, the determined lattice constants a = 10.460 Å, b = 4.630 Å, c = 11.100 Å, and β = 101.50° agree well with the experimental results.48 It is worth noting that the MAPbI3 crystal has a 3-dimensional structure with corner-sharing PbI6 octahedra, while the monohydrated phase MAPbI3·H2O is characterized by a 1-dimensional edge-sharing PbI6 structure. The optimized atomistic structures of water intercalated phase MAPbI3_H2O and monohydrated phase MAPbI3·H2O are shown in Fig. 1. It should be emphasized that the total energies per formula unit of MAPbX3_H2O are typically 0.3 eV higher than those of MAPbX3·H2O, indicating that the water intercalated phase would be an intermediate phase in a transformation to the monohydrated phase.
In order to compare the free energies of formation for pristine and hydrated phases, additional calculations of the harmonic phonon density of states were calculated using the codes Phonopy50 and VASP (PBEsol functional).51 The Gibbs free energy of formation (Gsolid) is calculated from the sum of the DFT internal energy (U), the vibrational entropy (Svib), and the configurational entropy (Sconf):
| Gsolid = U + PV − T(Svib + Sconf) | (1) |
3 Results
3.1 Water–perovskite interaction
For the water intercalated phase MAPbI3_H2O, the intercalated water molecule, with organic molecular MA+ ion, resides in the large interstitial space formed by a huge framework consisting of Pb and I atoms of inorganic PbI6 octahedra (for X = Br and Cl, similar structures are observed). It is bonded with H atoms of NH3 moiety of MA and I atoms of PbI6; the bond length between the O atom of water and the H atom of NH3 is ∼1.63 Å, and those between the H atoms of water and the I atoms of PbI6 are 2.43 and 2.54 Å. In Fig. 1(b) for the monohydrated phase MAPbI3·H2O, the corresponding bond lengths are observed to be slightly longer, i.e., 1.78, 2.83, and 2.92 Å. These indicate that the interactions between water molecule and inorganic PbI6 as well as organic MA are through hydrogen bonding, as already pointed out in the previous works.35,53,54When going from I to Br and to Cl, the (H2O)O–H(MA) bond length increases a little for the water intercalated phases or hardly change for the monohydrated phases, whereas the (H2O)H–X(PbX6) bond lengths decrease distinctly (see Table 1). On consideration that water intercalation causes a volume expansion, we estimate a relatively volume expansion rate as rvol = (V − V0)/V0 × 100%, where V is the volume of water intercalated or monohydrated phase and V0 the volume of pseudo-cubic MAPbX3 phase per formula unit. This gradually increases going from X = I to Br and to Cl. Consequently, it can be deduced that decreasing the atomic number of halogen component induces an enhancement of the interaction between water and inorganic PbX6 matrix through hydrogen bonding, while maintaining those interactions between water and the MA ion, resulting in the contraction of the interstitial space and the volume, which might cause difficulty of water intercalation and ion migration.
| X | O–H(MA) | H–X1 | H–X2 | r vol (%) | |
|---|---|---|---|---|---|
| MAPbX3_H2O | I | 1.63 | 2.43 | 2.54 | 7.10 |
| Br | 1.66 | 2.24 | 2.31 | 10.18 | |
| Cl | 1.69 | 2.09 | 2.15 | 13.39 | |
| MAPbX3·H2O | I | 1.78 | 2.83 | 2.92 | 4.40 |
| Br | 1.77 | 2.65 | 2.81 | 9.40 | |
| Cl | 1.79 | 2.34 | 2.83 | 10.21 |
To estimate the ease of water intercalation, we calculated the intercalation energy by
| Eint = EMAPbX3·H2O − (EMAPbX3 + EH2O) | (2) |
| X | E int | E dec | |
|---|---|---|---|
| MAPbX3_H2O | I | −0.53 | 0.47 |
| Br | −0.43 | 0.54 | |
| Cl | −0.36 | 0.60 | |
| MAPbX3·H2O | I | −0.87 | 0.81 |
| Br | −0.78 | 0.88 | |
| Cl | −0.69 | 0.92 |
We further considered decomposition of water intercalated and monohydrated phases by calculating the decomposition energy,
| Edec = (EPbX2 + EMAX + EH2O) − EMAPbX3·H2O | (3) |
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1) and MAX (space group: Fm
m1) and MAX (space group: Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), respectively. As shown in Table 2, the decomposition energies were calculated to be positive, indicating that the decomposition is an endothermic process. At this moment, it is worth to compare with those for the pristine perovskite halides without water. The decomposition of MAPbI3 → MAI + PbI2 is exothermic due to the negative decomposition energy of −0.06 eV, whereas those of MAPbBr3 and MAPbCl3 are also endothermic with the positive decomposition energies of 0.10 and 0.23 eV.14,15 Interestingly, the decomposition energy in magnitude is in the reverse order to the intercalation energy going from X = I to Br and to Cl. This indicates that water could intercalate more readily into the halide perovskite but the formed water-included compounds would be more resistant to decomposition into their relevant components as decreasing the atomic number of halogen component.
m), respectively. As shown in Table 2, the decomposition energies were calculated to be positive, indicating that the decomposition is an endothermic process. At this moment, it is worth to compare with those for the pristine perovskite halides without water. The decomposition of MAPbI3 → MAI + PbI2 is exothermic due to the negative decomposition energy of −0.06 eV, whereas those of MAPbBr3 and MAPbCl3 are also endothermic with the positive decomposition energies of 0.10 and 0.23 eV.14,15 Interestingly, the decomposition energy in magnitude is in the reverse order to the intercalation energy going from X = I to Br and to Cl. This indicates that water could intercalate more readily into the halide perovskite but the formed water-included compounds would be more resistant to decomposition into their relevant components as decreasing the atomic number of halogen component.
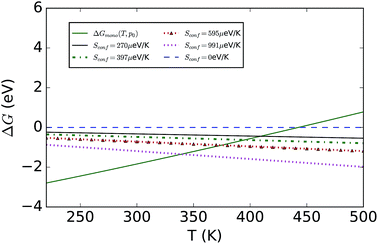
To consider finite-temperature effects, additional calculations were performed to compute the Gibbs free energy of each phase (see Fig. 2). Formation of the hydrated compound is found to be favourable at lower temperatures due to the large energy gain from creation of the hydrate versus a state containing MAPbI3 and water vapour. The calculations confirm the results stated earlier, but also predict that at higher temperatures the pristine MAPI3 phase is stabilised relative to the mono-hydrate by the increasing entropy of the water vapour and the vibrational entropy of the MAPI3 phase. The inclusion of configuration entropy associated with the rotational freedom of the MA+ ion acts to further stabilize the material against hydration.
3.2 Dynamics of water incorporation and charged defects
We turn our attention to how the ions and water molecule diffuse inside the water intercalated or monohydrated perovskites, trying to find out their role in material instability. It is well known that diffusion of ions in crystalline solid is associated with point defects such as a site vacancy and/or interstitial. While such migrations of ions or defects can provide explicit explanations for the performance of PSC device such as ionic conduction, hysteresis, and field-switchable photovoltaic effect,37–41,55–57 these might have important implications for material stability.It was established that, although as in other inorganic perovskite oxides several types of point defects could be formed in the hybrid perovskite halides, including vacancies (VMA, VPb, VX), interstitials (MAi, Pbi, Xi), cation substitutions (MAPb, PbMA) and antisite substitutions (MAX, PbX, XMA, XPb), vacancies except VPb have the lowest formation energies, while others are unstable both energetically and kinetically.41,57 In this work we thus considered only vacancies VMA and VX in the pristine, water-intercalated, and monohydrated phases, which could support vacancy-mediated ionic diffusion. For migration of the water molecule inside the water intercalated or monohydrated phases, water vacancy VH2O is formed and allowed to migrate.
For vacancy-mediated ion migration in the pristine and water intercalated MAPbX3 phases, we follow the three vacancy transport mechanisms established in the previous works,37,38,40 where vacancies are allowed to conventionally hop between neighbouring equivalent sites. According to these mechanisms, X− at a corner site of PbX6 octahedron migrates along the octahedron edge towards a vacancy in another corner site, and MA+ hops into a neighbouring vacant cage formed by the inorganic scaffold. Water molecule migrates along the similar path to MA+ case. For the cases of monohydrated phase, we have devised plausible paths for each of the three defects, and pick out one that has the lowest activation energy, as discussed below in detail. Fig. 3 shows the schematic view of vacancy-mediated ion and molecule migration paths. Special attention was paid to obtaining the well-converged structures of the start and end point configurations with structural relaxations with convergence criteria as 0.01 eV Å−1 atomic forces. The activation energies for these vacancy-mediated migrations are summarised in Table 3.
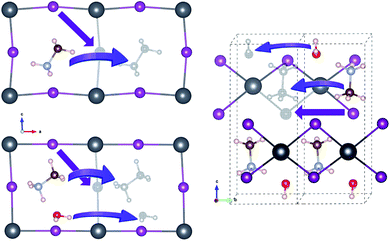 | ||
| Fig. 3 Schematic view of vacancy-mediated ion and molecule migrations in the pristine (left-top), water-intercalated (left-bottom), and monohydrated (right) perovskite halides. Colour scheme for atoms is the same to Fig. 1. | ||
| X | X− | MA+ | H2O | |
|---|---|---|---|---|
| MAPbX3 | I | 0.55 | 1.18 | |
| Br | 0.58 | 1.20 | ||
| Cl | 0.62 | 1.24 | ||
| MAPbX3_H2O | I | 0.22 | 0.38 | 0.28 |
| Br | 0.29 | 0.54 | 0.31 | |
| Cl | 0.35 | 0.63 | 0.42 | |
| MAPbX3·H2O | I | 0.44 | 1.14 | 0.78 |
| Br | 0.47 | 1.18 | 0.89 | |
| Cl | 0.49 | 1.23 | 1.08 |
To see whether our computational models and parameters could give reasonable results for the ionic migrations, the pseudo-cubic MAPbI3 was first tested. As listed in Table 3, the activation energies for I− and MA+ migrations were calculated to be 0.55 and 1.18 eV, respectively, which are comparable with 0.58 and 0.84 eV reported in ref. 37, and 0.32–0.45 and 0.55–0.89 eV in ref. 38, but higher than 0.16 and 0.46 eV in ref. 40. With respect to the crystalline lattice, we used the pseudo-cubic lattice as in the work in ref. 37, while Haruyama et al.38 and Azpiroz et al.40 used the tetragonal lattice. An exchange–correlation (XC) functional including dispersion (vdW) interactions was used in our work and the work in ref. 38, whereas PBEsol and PBE without vdW correction were used in ref. 37 and 40, respectively. Therefore, the slight discrepancies might be associated with the different crystalline lattices and XC functionals without vdW correction, not with the supercell size. Most important, the activation energy for I− migration is lower than that for MA+ migration in all the above-mentioned works, convincing that the results obtained in this work can be used to find out the influence of water on ion diffusion.
For I− migration in the monohydrated phase MAPbI3·H2O, which is structurally characterized by 1-dimensional edge sharing PbI6 octahedra connected in [010] direction, we devised four migration pathways along the three octahedron edges in different directions and across the space between separated octahedra. The lowest activation energy was found for the migration along the edge in [010] direction, while the highest value over 2 eV was found for the one across the space, implying this pathway less likely. Fig. 4 shows the I− migration pathways along the octahedron edge in the three kinds of phases and the corresponding activation energy profile. It is found that, when water intercalates into the perovskite, the activation energy decreases, indicating more facile diffusion of I− ion upon water intercalation. Meanwhile, the activation energy in the monohydrated phase is higher than in the water intercalated phase but still lower than in the pristine phase. This demonstrates that the intercalated water molecule enhances diffusion of ions in hybrid perovskite halides, facilitating the formation of hydrated phases. However, once the hydrated phase is formed, diffusion of ions becomes a little harder. Similar arguments hold for MAPbBr3 and MAPbCl3.
An MA+ ion in the monohydrated phase was enforced to migrate along the almost straight pathway in [010] direction since there is no channel in [100] direction due to the wall formed by PbI6 octahedra and the channel in [001] direction has much longer distance. It should be noted that MA+ cation in the water intercalated phase is allowed to diffuse equally both in [100] and [010] directions but not allowed to move in [001] direction due to the presence of water molecule on the path. Fig. 5 shows the intermediate states during MA+ migrations in the pristine, water-intercalated, and monohydrated MAPbI3 phases and the corresponding energy profile. We can see distortions of PbI6 octahedra during migration, much more clearly in the case of the water intercalated phase due to the rather strong interaction between PbI6 and methylammonium, which may cause difficult MA+ ion migration.
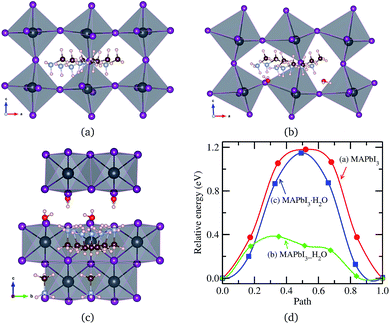 | ||
| Fig. 5 MA+ ion migration in (a) pseudo-cubic MAPbI3, (b) water intercalated phase MAPbI3_H2O and (c) monohydrated phase MAPbI3·H2O, and (d) corresponding activation energy profile. | ||
Relatively high activation energies for MA+ ion migrations were found for the pristine (1.18 eV) and monohydrated phases (1.14 eV), while low activation energy of 0.38 eV was found for the water intercalated phase. This indicates that inclusion of water in the perovskite halides reduces the activation energy for MA+ ion migration as in the case of halogen ion migration. As discussed above, the volume expansion rate of the water intercalated phase is larger than that of the monohydrated phase, and thus, water intercalation can induce much more space expansion, resulting in the enhancement of MA+ ion diffusion. When compared to I− migration, MA+ migration can be said to be more difficult due to higher activation energy in agreement with the previous works,37,38,40 in which the bottleneck comprising four I− ions and the high level of orientational motion of the MA+ ion were pointed out to be the reasons for such hard migration.
Finally, a H2O molecule was allowed to migrate in the same direction as MA+ ion in the water intercalated and monohydrated phases, as represented in Fig. 6. The activation energy in the water intercalated phase was calculated to be 0.28 eV, which is low enough to diffuse inside the bulk crystal and form the hydrated phase. As in the cases of ion migrations, this is lower than in the monohydrated phase. At this stage, it is worthwhile to compare with the initial process of water penetration into MAPbI3 surface. From the first-principles calculations,33,36,58 it was found that, when water molecules are brought into contact with MAPbI3 surface, the water molecule in the inside region is 0.2–0.3 eV more stable than the one in the outside region, and thus, the water molecule is strongly driven to diffuse into the inside of MAPbI3. The activation barrier for this process was calculated to be 0.31 eV (ref. 33) or 0.27 eV (ref. 36) at low coverage of water and 0.82 eV (ref. 33) at high coverage. These are comparable to the barrier of water diffusion within the bulk crystal in this work, which can be regarded as a continuation of the water penetration, indicating easy formation of water intercalated and further hydrated phase. As can be seen in Table 3, a water molecule can migrate more easily than a MA+ ion, which might be due to the larger molecular size of MA and its stronger interaction with environmental components, but has a lower activation barrier than X− ion in both phases. On the other hand, the activation barrier of water migration in the monohydrated phase is higher than the one in the water intercalated phase, as in the cases of X− and MA+ ion migrations.
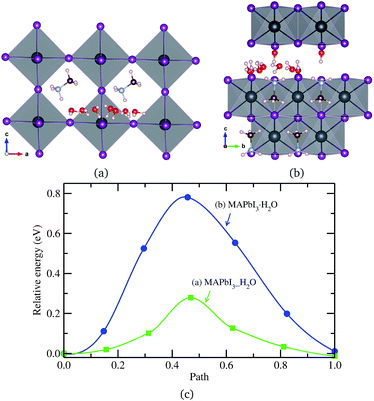 | ||
| Fig. 6 H2O molecule migrations in (a) water intercalated phase MAPbI3_H2O and (b) monohydrated phase MAPbI3·H2O, and (c) corresponding activation energy profile. | ||
When the atomic number of halogen component decreases from X = I to Br and to Cl, the activation barriers for ions and water molecule migrations increases monotonically, as shown in Table 3. In fact, when changing from I with larger ionic radius of 2.2 Å to Br with smaller ionic radius of 1.96 Å and to Cl with further smaller ionic radius of 1.81 Å, the lattice spacing and PbX6–MA bonding shrink while maintaining the intramolecular MA spacing.14,15 This results in the enhancement of Pb–X interaction and makes passages of ions and water molecule more difficult. Similar arguments hold for water intercalated and monohydrated phases. The increase of activation barrier for ion migrations going from X = I to Cl describes enhancement of material stability when mixed I atom with Br or Cl atom, and is coincident with aforementioned decomposition energetics.
4 Conclusion
To understand the degradation mechanism of perovskite solar cells upon exposure of MAPbI3 to moisture, we have investigated the influence of water intercalation and hydration on decomposition and ion migrations of MAPbX3 (X = I, Br, Cl) by first-principles calculations. The crystalline lattices and atomistic structures of water intercalated MAPbX3 phases were suggested and optimized, together with those of monohydrated phases MAPbX3·H2O. Water is found to interact with both the lead halide framework and the methylammonium ions through hydrogen bonding. The calculated results for water intercalation energies and decomposition energies indicate that water can exothermically intercalate into the hybrid perovskite halides, while the water intercalated and monohydrated compounds are stable with respect to decomposition. More importantly, the hydrogen bond interaction induced by water greatly affects the vacancy-mediated ion migrations, for which the activation barrier decreases upon the water inclusion inside the perovskite halides. The activation energies for ion and water molecule migrations become higher as going from X = I to Br and to Cl. These results clarify that degradation of PSCs upon moisture exposure originates from a multi-step process: the formation of water intercalated and hydrated compounds, followed by decomposition of these compounds, which provides insights to preventing this degradation at the atomic level.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work was supported partially by the State Committee of Science and Technology, Democratic People's Republic of Korea, under the state project “Design of Innovative Functional Materials for Energy and Environmental Application” (No. 2016-20). The research in the UK was supported by the Royal Society and the Leverhulme Trust, and the Imperial College High Performance Computing Service. A. P. M. was supported by a studentship from the Centre for Doctoral Training in Theory and Simulation of Materials at Imperial College London, funded by the EPSRC under grant no. EP/G036888. The calculations have been carried out on the HP Blade System C7000 (HP BL460c) that is owned and managed by Faculty of Materials Science, Kim Il Sung University. P. R. F. B. was supported by EPSRC grant no. EP/M025020/1 and EP/P02484X/1.References
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051 CrossRef CAS PubMed.
- N. J. Jeon, J. H. Noh, W. S. Yang, Y. C. Kim, S. Ryu, J. Seo and S. I. Seok, Nature, 2015, 517, 476–480 CrossRef CAS PubMed.
- D. Q. Bi, W. Tress, M. I. Dar, P. Gao, J. S. Luo, C. Renevier, K. Schenk, A. A. Abd, F. Giordano, J.-P. C. Baena, J.-D. Decoppet, S. M. Zakeeruddin, M. K. Nazeeruddin, M. Grätzel and A. Hagfeldt, Sci. Adv., 2016, 2, e1501170 Search PubMed.
- T. C. Sum and N. Mathews, Energy Environ. Sci., 2014, 7, 2518–2534 CAS.
- S. Luo and W. A. Daoud, J. Mater. Chem. A, 2015, 3, 8992–9010 CAS.
- Z. Xiao, Y. Yuan, Q. Wang, Y. Shao, Y. Bai, Y. Deng, Q. Dong, M. Hu, C. Bi and J. Huang, Mater. Sci. Eng., R, 2016, 101, 1–38 CrossRef.
- B. Hailegnaw, S. Kirmayer, E. Edri, G. Hodes and D. Cahen, J. Phys. Chem. Lett., 2015, 6, 1543–1547 CrossRef CAS PubMed.
- G. D. Niu, X. D. Guo and L. D. Wang, J. Mater. Chem. A, 2015, 3, 8970–8980 CAS.
- B. Li, Y. Li, C. Zheng, D. Gao and W. Huang, RSC Adv., 2016, 6, 38079–38091 RSC.
- D. Wang, M. Wright, N. K. Elumalai and A. Uddin, Sol. Energy Mater. Sol. Cells, 2016, 147, 255–275 CrossRef CAS.
- T. A. Berhe, W.-N. Su, C.-H. Chen, C.-J. Pan, J.-H. Cheng, H.-M. Chen, M.-C. Tsai, L.-Y. Chen, A. A. Dubaleb and B.-J. Hwang, Energy Environ. Sci., 2016, 9, 323–356 CAS.
- J. S. Manser, M. I. Saidaminov, J. A. Christians, O. M. Bakr and P. V. Kamat, Acc. Chem. Res., 2016, 49, 330–338 CrossRef CAS PubMed.
- Y.-Y. Zhang, S. Chen, P. Xu, H. Xiang, X.-G. Gong, A. Walsh and S.-H. Wei, 2015, arXiv:1506.01301.
- U.-G. Jong, C.-J. Yu, J.-S. Ri, N.-H. Kim and G.-C. Ri, Phys. Rev. B, 2016, 94, 125139 CrossRef.
- U.-G. Jong, C.-J. Yu, Y.-M. Jang, G.-C. Ri, S.-N. Hong and Y.-H. Pae, J. Power Sources, 2017, 350, 65–72 CrossRef CAS.
- J. H. Noh, S. H. Im, J. H. Heo, T. N. Mandal and S. I. Seok, Nano Lett., 2013, 13, 1764–1769 CrossRef CAS PubMed.
- H. Zhou, Q. Chen, G. Li, S. Luo, T.-B. Song, H.-S. Duan, Z. Hong, J. You, Y. Liu and Y. Yang, Science, 2014, 345, 542–546 CrossRef CAS PubMed.
- K. K. Bass, R. E. McAnally, S. Zhou, P. I. Djurovich, M. Thompson and B. Melot, Chem. Commun., 2015, 50, 15819–15822 RSC.
- J. You, Y. Yang, Z. Hong, T.-B. Song, L. Meng, Y. Liu, C. Jiang, H. Zhou, W.-H. Chang, G. Li and Y. Yang, Appl. Phys. Lett., 2014, 105, 183902 CrossRef.
- J. M. Frost, K. T. Butler, F. Brivio, C. H. Hendon, M. van Schilfgaarde and A. Walsh, Nano Lett., 2014, 14, 2584–2590 CrossRef CAS PubMed.
- G. D. Niu, W. Z. Li, F. Q. Meng, L. D. Wang, H. P. Dong and Y. Qiu, J. Mater. Chem. A, 2014, 2, 705–710 CAS.
- W. Huang, J. S. Manser, P. V. Kamat and S. Ptasinska, Chem. Mater., 2016, 28, 303–311 CrossRef CAS.
- J. Yang, B. D. Siempelkamp, D. Liu and T. L. Kelly, ACS Nano, 2015, 9, 1955–1963 CrossRef CAS PubMed.
- F. Hao, C. C. Stoumpos, Z. Liu, R. P. H. Chang and M. G. Kanatzidis, J. Am. Chem. Soc., 2014, 136, 16411–16419 CrossRef CAS PubMed.
- J. A. Christians, P. A. M. Herrera and P. V. Kamat, J. Am. Chem. Soc., 2015, 137, 1530–1538 CrossRef CAS PubMed.
- A. M. A. Leguy, Y. Hu, M. Campoy-Quiles, M. I. Alonso, O. J. Weber, P. Azarhoosh, M. van Schilfgaarde, M. T. Weller, T. Bein, J. Nelson, P. Docampo and P. R. F. Barnes, Chem. Mater., 2015, 27, 3397–3407 CrossRef CAS.
- B. Conings, A. Babayigit, T. Vangerven, J. D'Haen, J. Manca and H.-G. Boyen, J. Mater. Chem. A, 2015, 3, 19123–19128 CAS.
- S. Wozny, M. Yang, A. M. Nardes, C. C. Mercado, S. Ferrere, M. O. Reese, W. Zhou and K. Zhu, Chem. Mater., 2015, 27, 4814–4820 CrossRef CAS.
- D. Bryant, N. Aristidou, S. Pont, I. Sanchez-Molina, T. Chotchunangatchaval, S. Wheeler, J. R. Durrant and S. A. Haque, Energy Environ. Sci., 2016, 9, 1655–1660 CAS.
- Z. Xiao, D. Wang, Q. Dong, Q. Wang, W. Wei, J. Dai, X. Zeng and J. Huang, Energy Environ. Sci., 2016, 9, 867–872 CAS.
- J. Zhao, B. Cai, Z. Luo, Y. Dong, Y. Zhang, H. Xu, B. Hong, Y. Yang, L. Li, W. Zhang and C. Gao, Sci. Rep., 2016, 6, 21976 CrossRef CAS PubMed.
- H.-S. Ko, J.-W. Lee and N.-G. Park, J. Mater. Chem. A, 2015, 3, 8808–8815 CAS.
- C.-J. Tong, W. Geng, Z.-K. Tang, C.-Y. Yam, X.-L. Fan, J. Liu, W.-M. Lau and L.-M. Liu, J. Phys. Chem. Lett., 2015, 6, 3289–3295 CrossRef CAS.
- E. Mosconi, J. M. Azpiroz and F. de Angelis, Chem. Mater., 2015, 27, 4885–4892 CrossRef CAS.
- L. Zhang and P. H.-L. Sit, J. Phys. Chem. C, 2015, 119, 22370–22378 CAS.
- N. Z. Koocher, D. Saldana-Greco, F. Wang, S. Liu and A. M. Rappe, J. Phys. Chem. Lett., 2015, 6, 4371–4378 CrossRef CAS PubMed.
- C. Eames, J. M. Frost, P. R. F. Barnes, B. C. O'Regan, A. Walsh and M. S. Islam, Nat. Commun., 2015, 6, 7497 CrossRef CAS PubMed.
- J. Haruyama, K. Sodeyama, L. Han and Y. Tateyama, J. Am. Chem. Soc., 2015, 137, 10048–10051 CrossRef CAS PubMed.
- D. A. Egger, L. Kronik and A. M. Rappe, Angew. Chem., Int. Ed., 2015, 54, 12437–12441 CrossRef CAS PubMed.
- J. M. Azpiroz, E. Mosconi, J. Bisquert and F. de Angelisa, Energy Environ. Sci., 2015, 8, 2118–2127 CAS.
- M. H. Du, J. Mater. Chem. A, 2014, 2, 9091–9098 CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra and R. Car, et al. , J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- W. Geng, L. Zhang, Y.-N. Zhang, W.-M. Lau and L.-M. Liu, J. Phys. Chem. C, 2014, 118, 19565–19571 CAS.
- C.-J. Yu, U.-G. Jong, M.-H. Ri, G.-C. Ri and Y.-H. Pae, J. Mater. Sci., 2016, 51, 9849–9854 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- A. Poglitsch and D. Weber, J. Chem. Phys., 1987, 87, 6373–6378 CrossRef CAS.
- G. H. Imler, X. Li, B. Xu, G. E. Dobereiner, H.-L. Dai, Y. Rao and B. B. Wayland, Chem. Commun., 2015, 51, 11290–11292 RSC.
- B. R. Vincent, K. N. Robertson, T. S. Cameron and O. Knop, Can. J. Chem., 1987, 65, 1042–1046 CrossRef CAS.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- L. D. Whalley, J. M. Frost, Y.-K. Jung and A. Walsh, J. Chem. Phys., 2017, 146, 220901 CrossRef PubMed.
- C. Quarti, G. Grancini, E. Mosconi, P. Bruno, J. M. Ball, N. M. Lee, H. J. Snaith, A. Petrozza and F. de Angelis, J. Phys. Chem. Lett., 2014, 5, 279–284 CrossRef CAS PubMed.
- R. Gottesman, E. Haltzi, L. Gouda, S. Tirosh, Y. Bouhadana, A. Zaban, E. Mosconi and F. de Angelis, J. Phys. Chem. Lett., 2014, 5, 2662–2669 CrossRef CAS PubMed.
- J. M. Frost and A. Walsh, Acc. Chem. Res., 2016, 49, 528–535 CrossRef CAS PubMed.
- W.-J. Yin, T. Shi and Y. Yan, Appl. Phys. Lett., 2014, 104, 063903 CrossRef.
- A. Walsh, D. O. Scanlon, S. Chen, X. G. Gong and S.-H. Wei, Angew. Chem., Int. Ed., 2015, 54, 1791–1794 CrossRef CAS PubMed.
- E. Mosconi, A. Amat, M. K. Nazeeruddin, M. Grätzel and F. D. Angelis, J. Phys. Chem. C, 2013, 117, 13902–13913 CAS.
Footnote |
| † The pseudopotentials C.pbe-n-rrkjus_psl.0.1.UPF, H.pbe-rrkjus_psl.0.1.UPF, N.pbe-n-rrkjus_psl.0.1.UPF, Pb.pbe-dn-rrkjus_psl.0.2.2.UPF, and I(Br, Cl).pbe-n-rrkjus_psl.0.2.UPF were used. |
| This journal is © The Royal Society of Chemistry 2018 |