The crystal structure and electrical properties of the oxide ion conductor Ba3WNbO8.5†
Abstract
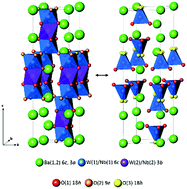
The structural and electrical properties of the hexagonal perovskite derivative Ba3WNbO8.5 have been investigated. Ba3WNbO8.5 crystallises in a hybrid of the 9R hexagonal perovskite and palmierite structure as recently reported for the novel oxide ion conductor Ba3MoNbO8.5. Ba3WNbO8.5 is also an oxide ion conductor and appears to exhibit oxide ionic conduction with negligible electronic conductivity over a wider pO2 range than Ba3MoNbO8.5. A neutron diffraction study has revealed that at 20 °C the average structure of Ba3WNbO8.5 contains just 13% of W(1)/Nb(1)O4 tetrahedra within the average structure of Ba3WNbO8.5 in comparison to 50% of Mo(1)/Nb(1)O4 tetrahedra in Ba3MoNbO8.5. The presence of (M/Nb)O4 tetrahedra with non-bridging apical oxygen atoms is an important prerequisite for the ionic conduction observed in the Ba3MNbO8.5 system (M = W, Mo). The strong reduction in the ratio of (M/Nb)O4 tetrahedra to (M/Nb)O6 octahedra upon replacement of W6+ for Mo6+ results in a reduction in the ionic conductivity by an order of magnitude at 450 °C. The bulk conductivities converge upon heating so that at 600 °C the bulk conductivity of Ba3WNbO8.5, σb = 0.0017 S cm−1, is comparable to that of Ba3MoNbO8.5 (σb = 0.0022 S cm−1). The results demonstrate that other members of the Ba3MM′O8.5 family can support oxide ion conductivity and further studies of hexagonal perovskite derivatives are warranted.
- This article is part of the themed collections: 2018 Journal of Materials Chemistry A HOT Papers and Advances in Solid State Chemistry and its Applications


 Please wait while we load your content...
Please wait while we load your content...