Open Access Article
Open Access ArticleStructure formation in soft nanocolloids: liquid-drop model†
A.-K.
Doukas
*ab,
C. N.
Likos
 c and
P.
Ziherl
ab
c and
P.
Ziherl
ab
aJožef Stefan Institute, Jamova 39, SI-1000 Ljubljana, Slovenia. E-mail: andreas.doukas@ijs.si
bFaculty of Mathematics and Physics, University of Ljubljana, Jadranska 19, SI-1000 Ljubljana, Slovenia
cFaculty of Physics, University of Vienna, Boltzmanngasse 5, A-1090 Vienna, Austria
First published on 17th April 2018
Abstract
Using a model where soft nanocolloids such as spherical polymer brushes and star polymers are viewed as compressible liquid drops, we theoretically explore contact interactions between such particles. By numerically minimizing the phenomenological free energy consisting of bulk and surface terms, we find that at small deformations the drop–drop interaction is pairwise additive and described by a power law. We also propose a theory to describe the small-deformation regime, and the agreement is very good at all drop compressibilities. The large-deformation regime, which is dominated by many-body interactions, is marked by a rich phase diagram which includes the face- and body-centered-cubic, σ, A15, and simple hexagonal lattice as well as isostructural and re-entrant transitions. Most of these features are directly related to the non-convex deformation free energy emerging from many-body effects in the partial-faceting regime. The phase diagram, which depends on just two model parameters, contains many of the condensed phases observed in experiments. We also provide statistical-mechanical arguments that relate the two model parameters to the molecular architecture of the polymeric nanocolloids, chain rigidity, and solvent quality. The model represents a generic framework for the overarching features of the phase behavior of polymeric nanocolloids at high compressions.
1 Introduction
The behavior of colloidal suspensions has long served as a key avenue to the understanding of condensed matter, elucidating many fundamental problems from irreversible aggregation1 and phase transition kinetics2 to Casimir forces3 and jamming.4 The part of this field concerned with the symmetry of colloidal crystals was initially focused on the face- and body-centered-cubic (FCC-BCC) dichotomy in micrometer-size particles5 and then on non-close-packed lattices6,7 as well as quasicrystals8,9 typical for soft nanocolloids including block-copolymer10–12 and surfactant micelles.13,14 Various theories were proposed to explain the stability of these structures, usually by employing microscopically-derived or postulated effective pair interactions.15–18 Alternatively, a heuristic model was also put forward, where the crystals are likened to a dry foam, that is to a space-filling assembly of completely faceted, polyhedral liquid drops.19 The relevance of this approach, which is based on an effective free energy consisting of a bulk and an interfacial term proportional to the contact area of neighboring particles, is supported by experiments and by simulations of diametral compression of a spherical polymer brush.20In dense suspensions where they spontaneously arrange into either disordered structures or crystal lattices, soft polymeric nanoparticles deform because they are pressed against one another. The overall deformation of a nanoparticle, which includes both redistribution and compression of the polymer chains, is generally not a simple sum of individual contributions associated with each pair of neighbors. The liquid-drop model20 captures the many-body effects involved in such a deformation without resorting to effective pair interactions, cluster or virial expansions, or some other commonly used approximation; in this respect, it is similar to the Widom–Rowlinson theory of the fluid state21 or to the concept of the Voronoi liquid.22 In the liquid-drop model, a polymeric nanocolloidal particle such as a spherical polymer brush or a dendrimer micelle is regarded as a compressible drop with a well-defined surface, and a crystalline or a disordered suspension of the nanoparticles is viewed as a concentrated emulsion of drops where the nearest neighbors are in contact such that a part of the surface of each drop is faceted.
For diametrically compressed single spherical polymer brushes (SPBs) this model preforms very well20 as reiterated by Fig. 1 showing the reduced central lateral extension ζ of an SPB confined to a slit formed by hard walls. At the qualitative level, the most striking feature of these results obtained in molecular-dynamics simulations20 is the knee-like onset of the deformation. Such a response can be associated with a liquid-like nature of the SPB where any small deformation is communicated across the whole of the SPB via the hydrostatic pressure, and this is indeed reproduced by the fit based on the liquid-drop model; in an elastic sphere, on the other hand, small indentations lead to localized subsurface deformations23 and thus to a much more gradual increase of the lateral extension on compression. Also in excellent agreement are the deformation energies. This holds for compressions down to 40% of SPB's resting diameter, that is well beyond the small-deformation regime.
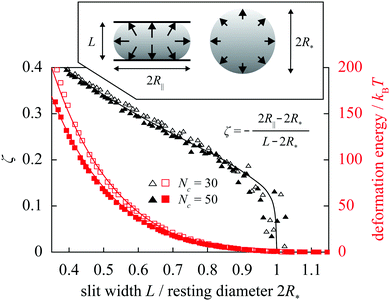 | ||
| Fig. 1 Reduced central lateral extension ζ of a diametrically compressed spherical polymer brush with f = 60 arms containing Nc = 30 and 50 monomers plotted against slit width L (black datapoints/curve). The datapoints are obtained using molecular-dynamics simulations and the curve is the liquid-drop-model fit for the reduced Egelstaff–Widom length Ψ = 0.6 [Ψ and the resting diameter of the drop R* are defined in eqn (2) and immediately below it, respectively]. Also shown are the deformation energies for these two cases together with the fits (red datapoints/curves). Inset illustrates the diametral-compression geometry, with arrows representing hydrostatic pressure, and contains the definition of ζ. | ||
Here we numerically explore the liquid-drop model in order to study the interactions between the drops at both small and large deformations and to compute their phase diagram. We show that the behavior of the drops in the partial-faceting regime is rather special: for a suitable choice of model parameters, this regime is characterized by a non-convex deformation free energy, and the differential tensions of the contact zones and the drop–solvent interface lead to several unique features that are neither present in the complete-faceting limit nor can be anticipated based on it.19 Our central result is a very rich phase diagram, which is controlled by just two model parameters but still contains most of the experimentally observed lattices, and, interestingly, some isostructural and re-entrant transitions. We also provide a detailed theoretical interpretation of the small-deformation drop–drop interaction, which paves the way to numerical simulations of the liquid-drop model at densities just beyond the fluid–solid transition, and we show that the model can be considered as a micromechanical framework leading to shoulder-like repulsive pair interactions24 known to lead to a range of interesting phenomena from clustering16,25 to formation of quasicrystals.18,26
2 The model
In the liquid-drop model, the micromechanics of a suspension of soft nanoparticles is defined by the free energy of each drop which consists of a phenomenological bulk term and of two surface terms, one for the drop–solvent interface and the other for the drop–drop contact zones. Like in ref. 20, we choose a bulk term based on the Murnaghan equation of state27 so that the free energy per drop reads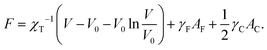 | (1) |
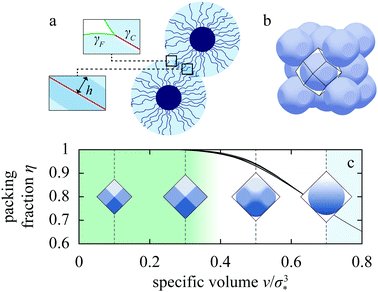 | ||
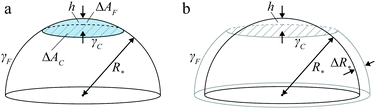
| Fig. 2 Liquid-drop model. (a) Schematic of two spherical polymer brushes in contact; the drop–solvent and drop–drop interfacial tensions are denoted by γF and γC, respectively, and h is indentation. (b) FCC lattice of partially faceted Ψ = 1, ω = 1 drops showing the Wigner–Seitz cell around one of the drops. (c) Side views of Ψ = 1, ω = 1 drop in FCC lattice at four representative specific volumes v/σ*3, illustrating the partial- and complete-faceting regimes. Also plotted is the packing fraction η for drops at reduced Egelstaff–Widom length Ψ = 0.1, 1, and 10 and tension ratio ω = 0.7, 0.9, 1.1, and 1.3 (solid curves); Ψ and ω are defined in eqn (2) and (3), respectively. As η barely depends on Ψ and ω, we omit the labels. | ||
In a dense emulsion, neighboring drops are pressed against each other as illustrated in Fig. 2b and are thus either partially or completely faceted depending on packing fraction η defined as the ratio of the physical volume of the drop V and its specific volume v = ρ−1, where ρ is the drop number density (Fig. 2c). The deformation energy of a faceted drop is measured relative to the resting isolated-drop state, and it depends on drop compressibility encoded by the so-called reduced Egelstaff–Widom length and on the propensity of drops to either aggregate or repel each other, which is in turn controlled by the relative magnitude of the drop–drop and drop–solvent interfacial tensions. The reduced Egelstaff–Widom length is an intrinsic property of the drop best appreciated by considering it in isolation. An isolated drop is pressurized by the tension of the drop–solvent interface and thus its resting volume V* is smaller than the reference volume V0. To lowest order, the relative volume decrease is given by the product of the Laplace pressure of the reference drop of radius R0 = (3V0/4π)1/3 and χT:
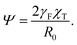 | (2) |
The shape of drops in emulsion does not depend only on Ψ but also on number density, local packing geometry, and the ratio of the drop–drop and the drop–solvent interfacial tensions defined by
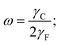 | (3) |
To construct the phase diagram, we numerically evaluate the deformation free energies of drops arranged in nine trial lattices. The deformation free energy ΔF is defined as the difference between the free energy per drop in a given lattice and at a given density (or specific volume) and the free energy of an isolated drop in resting state, and we compute it using the Surface Evolver package29 and the cell approximation first developed by Lennard-Jones and Devonshire as a model for the fluid state.30 In this approximation, each drop is confined to a cage formed by its neighbors (Fig. 2b) and mimicked by the corresponding Wigner–Seitz polyhedron, and the drop–drop contact zones are assumed to be flat as illustrated by the faceted drops in Fig. 2c.
The nine trial lattices considered here include (i) five cubic lattices—simple cubic (SC), FCC [indistinguishable from the hexagonal-close-packed lattice (HCP) within our model], BCC, diamond cubic (DC), and A15—as the usual candidates in case of particles devoid of a priori directional interactions, (ii) the body-centered-tetragonal (BCT) lattice as a generalization of the BCC lattice, and (iii) the σ and simple hexagonal (SH) lattice. The last two trial lattices were chosen because they were experimentally observed7 and the rationale behind their stability is unclear. The geometric parameters of all but the σ lattice are listed in Table I of ref. 23; for the σ lattice see, e.g., ref. 31.
The minimal-energy shape of drops in each lattice is obtained numerically using the Surface Evolver package.29 The estimated overall numerical inaccuracy of the deformation free energy generally does not exceed about 0.1% except at very small deformations. In singe-site-type lattices such as the SC, FCC, BCC, BCT, and DC lattice, there exists a single Wigner–Seitz cell, and the force balance for each drop is automatically guaranteed by the symmetry of the cell. The A15 and the σ lattice have 2 and 5 inequivalent sites, respectively. Here force balance at each contact zone was ensured by slightly adjusting the positions of the planes that define the Wigner–Seitz cells such that the area of the contact zone viewed from either of the two drops was the same (ESI,† Section I), and the deformation energy per drop is computed as a suitably weighted average over the inequivalent sites.
3 Drop–drop interaction
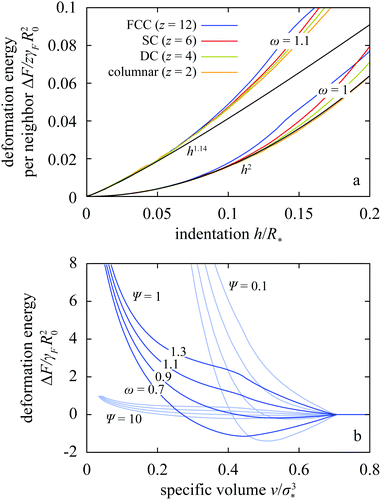
As mentioned above, the phase diagram is obtained based on the deformation free energies of the trial lattices, and we compute these energies by compressing drops confined to the corresponding Wigner–Seitz cells from the point where the drops come in contact down to a small enough specific volume v. The deformation energies are also interesting per se because they allow us to distinguish between the pairwise-additive drop–drop interaction regime and the manifestly many-body regime, and we first address this issue. To this end, we plot ΔF for the trial lattices as a function of indentation h defined as half the difference between the resting diameter σ* and drop–drop center-to-center distance (Fig. 2a).3.1 Pairwise-additive regime
In Fig. 3a we compare ΔF(h) per neighbor for moderately compressible Ψ = 1 drops arranged in a columnar, DC, SC, and FCC lattice with z = 2, 4, 6, and 12 regularly distributed neighbors, respectively.32 This figure shows results for two representative tension ratios ω = 1 and 1.1. In both cases, ΔF per neighbor is the same in all four lattices as long as indentation h is small compared to the resting radius R*. This shows that for h/R* ≪ 1, the interaction is indeed pairwise additive. The overlapping portions of curves in Fig. 3a extend up to h/R* ≈ 0.10 and 0.05 at ω = 1 and 1.1, respectively.The pairwise-additive deformation energy is described by a power law hp seen at all Ψ and ω (ESI,† Section II); at ω = 1 the exponent p ≈ 2.0 is a little smaller than in incompressible wet foam33 but as ω is increased it saturates at 1.14. On the other hand, at tension ratios smaller than 1 the drops are attractive on contact because the drop–drop interfacial tension is smaller than the drop–solvent tension as witnessed by Fig. 3b and Fig. S4 of ESI.† If the tension ratio is smaller than about 0.9, the attractive interaction is also characterized by a power law at small indentations, the exponent being about 0.89 (ESI,† Section II and Fig. S4 and S5).
This behavior can be explained using analytical arguments pertaining to a single contact zone (ESI,† Section II). We consider the change in total free energy due to faceting, and we calculate the terms proportional to h and h2. The first effect of interest is related to the change of the surface free energy ΔFA associated with the increase of the contact area and the decrease of non-contact area upon faceting. If we approximate the shape of a faceted drop by a truncated sphere and assume that its radius remains equal to the resting radius R* (Fig. 4a), then we find that ΔFA = 2π(ω − 1)γFR*h − πωγFh2. This result contains the leading-order term in the deformation free energy 2π(ω − 1)γFR*h, which agrees well with the numerical results in the small-indentation regime both in attractive and in repulsive drops with ω < 1 and ω > 1, respectively (Fig. 3b and Fig. S4 in ESI†). The second-order term is somewhat more involved and it depends on two additional effects rather than just on the surface free energy. In very compressible drops with Ψ ≫ 1 where the radius is not expected to change after two drops come in contact, indentation is also associated with an increase of the bulk energy because the drop volume is decreased and this is associated with mechanical work against pressure. The corresponding change of the bulk energy is ΔFbulk = 2πγFh2 so that the total deformation free energy reads
| ΔF ≈ 2π(ω − 1)γFR*h + 2π(1 − ω/2)γFh2, | (4) |
Our analytical result for the drop–drop interaction energy [eqn (4)] is also interesting because it does not involve any assumptions concerning the relative location of the different contact zones apart from that they should not overlap. As such, it is equally applicable to drops that form crystals as well as to drops in the less symmetric local configurations typical for fluids and glasses. This means that it can be used as input in, e.g., theoretical or simulation studies of disordered structures of liquid drops, allowing one to explore the finite-temperature phase diagram, the equilibrium dynamics, the rheology of a suspension of drops etc. at intermediate densities in greater detail.
3.2 Many-body regime
If the indentation h/R* is not small, one enters the regime where many-body interactions are manifest and ΔF is determined by the geometry of the whole cage around the drop, much like in incompressible bubbles in soft jammed materials.34 The kinks in the FCC curves in Fig. 3a seen at h/R* ≈ 0.135 show that ΔF is not necessarily a strictly convex function of indentation. This is more clearly visible in Fig. 3b where we plot the FCC deformation energy vs. specific volume for Ψ = 0.1, 1, and 10 and various ω. In moderately compressible drops with Ψ = 1, a large enough tension ratio of ω ≳ 1.1 gives rise to a hump in the energy whereas tension ratios ω smaller than 1 make the energy decrease on compression, rendering particles attractive upon contact. As shown in Fig. 3b, the hump is absent at small enough Ψ. The value of Ψ below which ΔF is strictly convex cannot be read off Fig. 3b where a common scale is employed so as to emphasize the role of drop compressibility; this point is discussed in detail in Section III of ESI.†The non-convex and non-monotonic profiles of ΔF are also seen in other lattices as shown in Fig. S8b–e of ESI,† and they are particularly interesting because they provide a basis for a complex phase diagram, which may potentially include isostructural and re-entrant transitions.35,36 As elaborated in Section 4 of ESI,† non-convexity and non-monotonicity are directly associated with the partial-faceting regime where our model is reminiscent of wet foam (ESI,† Section IV), and they are absent in the complete-faceting regime covered in ref. 19.
4 Phase diagram
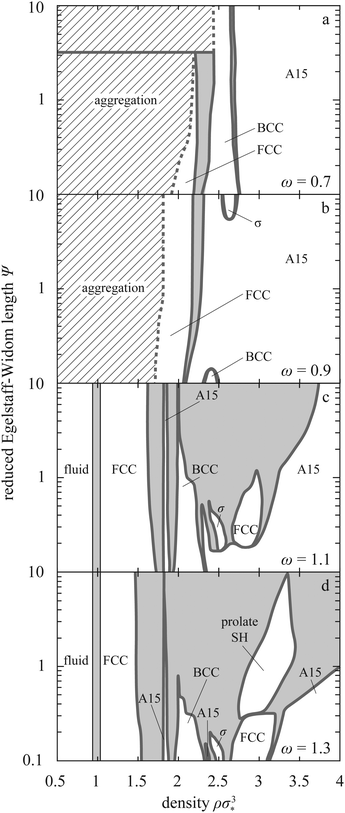
We now compute the phase diagram in the (Ψ,ρσ*3)-plane at T = 0 where the entropy due to lattice oscillations of drops vanishes. The restriction is not unrealistic for crystalline phases, because the entropic contribution arising from the kinetic degrees of freedom of the drops in such phases—which can be analytically calculated within the harmonic-solid approximation and is of the order of kBT—is typically considerably smaller than the potential (in our case, deformation) free energy. We examine the range of Ψ at the crossover between hardly compressible and very soft drops, and we combine our results with those pertaining to fluid–solid transition in hard spheres.37The main features of the phase diagram at tension ratios ω < 1 where the drops are attractive are aggregation at small densities, narrow coexistence regions, and only a handful of stable lattices (FCC, BCC, σ, and A15; Fig. 5a and b).
For ω < 1, drops form aggregates as soon as they come in contact. The structure of the stable aggregate is either FCC or BCC, the latter minimizing the free energy at small ω and large Ψ. For example, at ω = 0.7 our theory predicts that aggregates form BCC and FCC crystals for Ψ ≳ 3 and Ψ ≲ 3, respectively, as witnessed by Fig. 5a; at ω = 0.65 the transition is at Ψ ≈ 1 (ESI,† Fig. S12). The density of the aggregates plotted using dashed line in Fig. 5a and b varies with ω and Ψ (ESI,† Section V). Once the system is compressed beyond this point, it undergoes a few solid–solid transitions. The exact phase sequence depends on ω and Ψ but it always ends with the A15 lattice as expected in the complete-faceting regime.19
For ω > 1, the interparticle interaction is purely repulsive, which stabilizes the fluid phase at small densities (Fig. 2c and d). The phase diagram includes the FCC lattice immediately after the fluid phase and again invariably terminates with the A15 lattice at large densities. But unlike its ω < 1 counterpart, the ω > 1 phase diagram is very elaborated. Apart from the low-density FCC and the high-density A15 lattice, the phase sequence includes the low- and intermediate-density A15, BCC, σ, the high-density FCC, and SH phase with c/a between 1.4 and 1.7. The diagram is marked by re-entrant FCC and A15 phases as well as by isostructural A15–A15 transition at large Ψ and by the SH phase, which consists of the oblate c/a < 1 region and a prolate c/a > 1 region at ω > 1.5 (ESI,† Section VI).
Compared to the phase diagram of elastic spheres,23 the ω > 1 part of Fig. 5 contains more elaborate phase sequences and phase coexistences are generally considerably broader. These features may be used to qualitatively decide whether a given experimental soft-particle system is better described by the elastic-sphere or the liquid-drop model. In this context, also telling may be the high-density behavior where the elastic-sphere model predicts either A15 or SH lattice with c/a ≈ 1 depending on Poisson's ratio and on the underlying elastic theory whereas the liquid-drop model points solely to the A15 lattice.
At ω ≳ 1.2, the phase diagram contains most lattices typically observed in soft nanocolloids,7,8 which is encouraging. Also reassuring is the busy intermediate-density part of the phase diagram at Ψs that are not too large and at ρσ*3 between about 1.5 and 3, which implies that the theoretically predicted lattices may be seen at moderate compressions not too far beyond the fluid–solid transition.
The predictions summarized by the theoretical phase diagrams in Fig. 5 are a direct consequence of the characteristic dependence of the deformation free energy on the specific volume, which is in turn intimately related to the surface energy of the drops as we will now show. To this end, we first recall that the surface area of a body of volume V is given by A = wV2/3, where w is a dimensionless shape factor. Up to the density where they come in contact, the drops are spherical and w = 62/3π1/3 ≈ 4.836. Beyond this point they are partially faceted and this leads to an increase of the shape factor which saturates at a value characteristic for a given lattice; in FCC and SC lattice, at wFCC ≈ 5.345 (rhombic dodecahedron) and wSC = 6 (cube), respectively.
The shape deformation upon compression thus modifies the A = wV2/3 scaling law, and the onset of faceting can be depicted as a shift from the sphere branch with w ≈ 4.836 to a complete-faceting branch (dashed curves in Fig. 6; shown here is the FCC branch with w ≈ 5.354). Since the latter lies higher than the former, the shift partly compensates for the area decrease due to compression and the total area of the drop changes only little in the partial-faceting regime (Fig. 6).
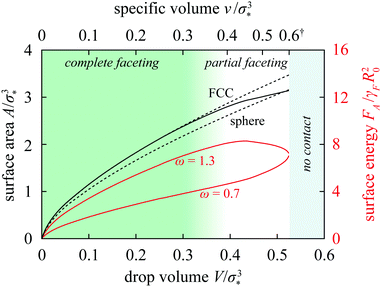 | ||
| Fig. 6 Surface area and surface energy of a drop in the Ψ = 1 FCC lattice vs. drop volume. The dashed lines show the area of a sphere and of the rhombic dodecahedron, and the solid black line is the exact area of the Ψ = 1 drop in the FCC lattice. Red lines are the surface energies of the drop for ω = 0.7 and 1.3. Also indicated are the no-contact, partial-faceting, and complete-faceting regimes and the specific volume on the secondary horizontal axis. (†: As shown in ESI,† Section VII, this axis is strongly nonlinear at v ≳ 0.5 and since the v/σ*3 = 0.6 and 0.7 tick marks are extremely close to each other, the latter is not drawn for clarity.) | ||
More importantly, the growth of the contact zones at the expense of the drop–solvent interface represented by this shift can be associated with a rather peculiar variation of total surface energy if the tensions of the drop–solvent interface and the drop–drop interface are not too similar, e.g., if the tension ratio is not too close to 1. In particular, if ω > 1 then the surface energy features a maximum; at ω = 1.3, this maximum is rather prominent as shown by the upper red curve in Fig. 6. The maximum then leads to a hump in the total deformation energy provided that the bulk term is not too large.
On the other hand, if ω < 1 then formation of contact zones is energetically favorable as elaborated in Section 3 of ESI† and this drives attraction between the drops. As a result, the total surface energy decreases upon compression by more than in drops with tension ratio equal to 1. This leads to a non-monotonic deformation free energy characterized by a minimum at a specific volume smaller than that at contact as witnessed by the ω = 0.7 and 0.9 curves in Fig. 3b; the depth and the location of the minimum naturally also depend on the bulk free energy of the drop. Thus we see that the non-convex and non-monotonic free-energy profiles rely both on the differential surface tension and a large enough compressibility; the mechanism at work is independent of the details of the bulk term, here described by the Murnaghan equation of state, and is thus generic.
5 Discussion
The phase diagram in Fig. 5 can be tested experimentally, most straightforwardly by compressing a solution of soft nanoparticles at fixed experimental parameters, say temperature and pH. The first aspect of the diagram that can be exploited to facilitate comparison with experiments is its weak dependence on Ψ at small and intermediate densities. Our theoretical predictions for the drop–drop interaction at small deformations [eqn (S4) and its dimensionless variant eqn (S10) in ESI†] suggest that in the small-indentation regime where the deformation free energy is pairwise-additive, the reduced Egelstaff–Widom length Ψ merely affects the magnitude of the interaction. As a result, the phase diagram should be independent of Ψ in this regime; in other words, the phase boundaries in the (ρσ*3,Ψ) plane should be vertical. To a fairly good approximation, this is indeed the case for ω > 1 for reduced densities up to ρσ*3 about 2. For example, at ω = 1.3 the boundaries of both the low-density FCC and the low-density A15 phase are essentially the same irrespective of Ψ. In attractive particles, i.e. for ω < 1, the phase boundaries are also independent of Ψ except at very small Ψ: At ω = 0.7, e.g., all five phase transition densities shown in Fig. 5a depend a little on Ψ but only for Ψ ≪ 1.A direct consequence of the above behavior is that the experimentally observed transitions at small-to-intermediate densities can be used to estimate the tension ratio ω as one of our model parameters. On the other hand, the phase sequence at large densities where pairwise-additivity no longer holds generally depends on the Egelstaff–Widom length Ψ as witnessed by Fig. 5. To relate the observed phase sequences to the microscopic features of the nanocolloids, it is important to understand how Ψ is controlled by particle architecture, chain stiffness, solvent quality etc.; also of interest is the microscopic origin of the tension ratio ω. Below we present scaling-theory estimates of the orders of magnitude of Ψ and ω, and we also discuss some other theoretical implications of the liquid-drop model.
5.1 Theoretical estimates of reduced Egelstaff–Widom length Ψ and tension ratio ω
The Egelstaff–Widom length defined by eqn (2) depends on the surface tension and compressibility of the nanoparticle. Within the context of the liquid-drop model, these quantities are viewed as effective material parameters: γF does not represent only the bare polymer–solvent interactions (which in good solvents correspond to negative real surface tension) but also chain connectivity, which is in turn neglected in the bulk term where the monomers are treated as a liquid. Both γF and χT are related to the osmotic equation of state Π(ψ) which depends on the density of monomers within the nanocolloid ϕ = N/V*, where N is the number of monomers and V* = 4πR*3/3 is the resting volume of the particle. In the resting state, the effective surface tension γF is proportional to Π according to the Laplace law: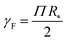 | (5) |
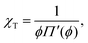 | (6) |
Eqn (5) and (6) suggest that within the scope of scaling theory, the reduced Egelstaff–Widom length is given by
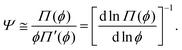 | (7) |
This relation can now be used to estimate the magnitude of Ψ depending on the monomer density as well as to examine the effects of cross-linking and chain stiffness.
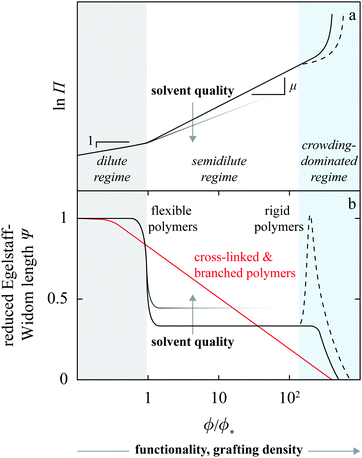
Let us first examine the effect of monomer density. In dilute polymer brushes where ϕ is smaller than the overlap density, the osmotic pressure is described by the van’t Hoff law38 and proportional to the monomer density, Π ∝ ϕ (Fig. 7a), so that
| Ψ ∼ 1 | (8) |
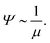 | (9) |
In both the dilute and the semidilute regimes, the Egelstaff–Widom length Ψ thus does not depend on the monomer concentration, hence the step-like profile depicted by Fig. 7b. However, as the monomer density is increased further and the behavior of the brush becomes crowding-dominated, the osmotic pressure is no longer described by a power law and so Ψ is not a constant. The increasingly more steep Π(ϕ) characteristic of this regime (Fig. 7a and Fig. 1 in ref. 39) leads to a gradual decrease of Ψ. This behavior can be illustrated using a model equation of state which diverges at a finite “jamming limit” ϕ0, say Π(ϕ) ∝ (ϕ − ϕ0)−m, which gives
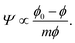 | (10) |
We can apply the same line of thinking to brushes consisting of rigid rather than flexible polymers as well as to branched and cross-linked polymers. In the former, the crossover from the semidilute to crowding-dominated regime is cusp-like as shown in, e.g., Fig. 10 in ref. 40 and summarized by the dashed line in Fig. 7a. The corresponding reduced Egelstaff–Widom length Ψ has a peak at the crossover and then decays with ϕ much like in flexible chains. The exact shape of the peak and its height clearly depend on the cusp in the osmotic pressure, which may be either gentle or pronounced.
In branched and cross-linked polymers, osmotic pressure naturally also increases with monomer density like in linear chains. As a result, Ψ should generally fall off with increasing ϕ but because these polymers are not self-similar, this should happen in a gradual rather than in a step-like fashion like in linear chains. This behavior is also shown in Fig. 7b.
In experiments, the reduced Egelstaff–Widom length is not determined solely by chain grafting density or functionality and polymer architecture but also by solvent quality, which modifies the osmotic equation of state in the semidilute regime. In turn, solvent quality is controlled by temperature or pH. If they are held constant, then Ψ is constant too and a compression run from small to large particle density would correspond to a horizontal trajectory across the theoretical phase diagram in Fig. 5. However, in an experiment where temperature were varied, a heating run would be represented by a diagonal trajectory from the small-Ψ, small-ρ region to the large-Ψ, large-ρ region because a rise in temperature both improves solvent quality and increases the size of polymer nanoparticles dissolved in organic solvents, water being an exceptional solvent for which the quality worsens with increasing temperature (Fig. S20 in ESI†).
Our next task is to estimate the physically relevant range of the tension ratio ω. Here too we turn to scaling arguments so as to evaluate the dependence of the effective drop–solvent and drop–drop tensions γF and γC, respectively, and we focus on star polymers. The former was shown to scale as20
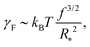 | (11) |
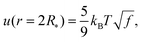 | (12) |
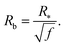 | (13) |
Eqn (12) and (13) finally give
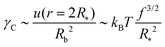 | (14) |
| ω ∼ 1 | (15) |
This estimate is important because it shows that the tension ratio ω is generally not very different from unity, which in turn implies that by a suitable choice of endgroups both the attractive ω < 1 and the repulsive ω > 1 regimes are achievable. Such a conclusion is consistent with experiments reporting aggregation in end-functionalized star and brushes41–43 as well as stable, non-aggregated dispersions of stars based on homopolymers, thereby proving that by a suitable modification of endgroups one may control ω. In addition, eqn (15) shows that the range of model parameters scanned in this paper does include most of the experimentally relevant cases.
5.2 Liquid-drop model vs. shoulder interactions
Apart from relevance for experiments, our main predictions are also interesting from a broader statistical-mechanical perspective. In the 1970s, non-convex thermodynamic potentials were employed to interpret the melting curve and isostructural transitions in some rare earths,44 where they were associated with shoulder-like pair interactions attributed to the promotion of valence electrons to vacant orbitals expected to take place upon compression.24 The connection between shoulder-like interactions and isostructural transitions is illustrated in Fig. 8a.36 Here we schematically plot the overlap energy of a crystal formed by particles with such a potential, for clarity also characterized by a large enough hard core so as to prevent overlap of next-nearest neighbors. This energy vanishes at large specific volumes where the system essentially behaves as a hard-core ensemble, with the particles avoiding each other. On the other hand, once the specific volume is small enough they must overlap but the penalty for doing so does not depend on specific volume because of the shape of the shoulder interaction. The corresponding step-like profile of the overlap energy is to be combined with the entropic term, which increases upon compression, and at low enough temperatures the total free energy features a hump. This hump may give rise to an isostructural transition in the lattice considered provided that no other lattice intervenes at specific volumes where the free energy is non-convex.This mechanism is very appealing, providing a simple and transparent interpretation for an uncommon phenomenon. Since they were first introduced, square-shoulder and the antipodal but related square-well interactions were explored in many different contexts including clustering,16,25 liquid–liquid transitions,45 glasses,46 quasicrystals,18,47 water anomalies48 (which were also rationalized using the linear-ramp interaction,49) etc. In most of these cases, the explanation obtained based on these model potentials seems the most plausible one despite the admittedly idealized form of the potentials, which can be thought to mimic, e.g., the interaction of soft polymeric nanoparticles such as dendrimers.50 Although shoulder-like interparticle interactions can also be induced in certain reduced-dimensionality systems by relying on an external field,51,52 it is fair to say that there do not exist many realistic systems that may be directly linked with these model pair potentials.
Our findings demonstrate that non-convex thermodynamic potentials and thus some of the phenomenology associated with the shoulder-like potentials can be reproduced within the liquid-drop model for a suitable choice of parameters. This is illustrated by the FCC deformation free energies in Fig. 3b, some of which are non-convex, but even more clearly by the superposition of the Ψ = 1, ω = 1.3 energies for four distinct lattices plotted in Fig. 8b. These energies differ in several ways—the specific volume where the drops in a lattice first touch each other, the location of slope discontinuities separating regimes with different numbers of contacts with neighbors, etc.—and the differences are important or else the phase diagram would be more bland than it is. Yet the common features and the quantitative similarities of these curves are far more remarkable: the location of the hump does not vary very much and the hump itself is equally prominent in all four cases. This agreement suggests that these lattices can be mapped onto a shoulder-like potential, which may thus be viewed as an effective description of an actual physical system as simple as a compressible liquid drop, albeit in the regime where drop–drop forces are many-body. In other words, an emulsion of monodisperse liquid drops can be considered as an exact micromechanical model for some of the effects associated with shoulder-like potentials.
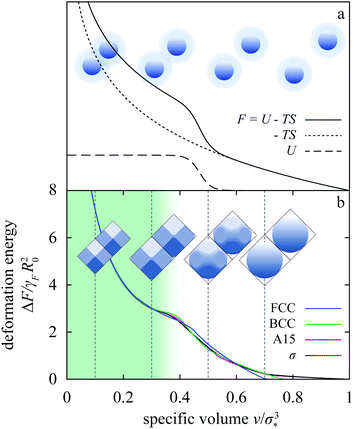 | ||
| Fig. 8 Schematic of the free energy of a system of particles interacting with a hard-core/square-shoulder pair potential at a finite-temperature,36 where the abrupt onset of overlap energy at an intermediate density gives rise to a hump in the free energy (a). The cartoons illustrate the typical non-overlapping and overlapping configurations in particles. Panel b shows the superposed Ψ = 1, ω = 1.3 deformation free energies of the FCC, BCC, A15, and σ lattice within the T = 0 liquid-drop model. Although not identical, the free energies of these lattices are remarkably similar. Also included are snapshots of the drop in the FCC lattice. | ||
The analogy is not entirely complete because the version of the liquid-drop model presented here does not include the translational entropy of the drops. On the other hand, if the drops are to be regarded as models of spherical polymer brushes, the entropy due to the internal motion of the polymer chains is there as witnessed by the ideal-gas-type ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V term in the free energy [eqn (1)]. At large compressions, we may expect that this part of the entropy is dominant and so the liquid-drop model should be rather accurate whereas the intermediate-compression regime can be studied using simulations based on the analytical drop–drop interaction [eqn (4)].
V term in the free energy [eqn (1)]. At large compressions, we may expect that this part of the entropy is dominant and so the liquid-drop model should be rather accurate whereas the intermediate-compression regime can be studied using simulations based on the analytical drop–drop interaction [eqn (4)].
6 Conclusions
Apart from elaborating its rich phase diagram, this work points to several aspects of the liquid-drop model to be explored in the future. The power-law small-indentation interaction can be used to numerically study the structure, dynamics, and rheology of disordered liquid-drop systems, which would provide a fresh insight into many experiments.53 Especially intriguing is the almost linear-ramp repulsion, which is expected to give rise to an anomalously small shear modulus of the low-density FCC lattice. Lastly, by mapping the liquid-drop model onto effective pair potentials such as square-shoulder, square-well, and linear-ramp interaction one would make the theoretical predictions obtained based on these interactions much more realistic.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We thank L. Athanasopoulou, G. Kahl, R. D. Kamien, E. Lomba, A. Šiber, T. Urbič, and N. B. Wilding for helpful discussions. This project has received funding from the European Unions Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie ETN COLLDENSE, grant agreement No. 642774, and the authors acknowledge the financial support from the Slovenian Research Agency (research core funding No. P1-0055).References
- D. A. Weitz and M. Oliveria, Phys. Rev. Lett., 1984, 52, 1433 CrossRef CAS.
- V. J. Anderson and H. N. W. Lekkerkerker, Nature, 2002, 416, 811 CrossRef CAS PubMed.
- C. Hertlein, L. Helden, A. Gambassi, S. Dietrich and C. Bechinger, Nature, 2008, 451, 172 CrossRef CAS PubMed.
- M. E. Cates, J. P. Wittmer, J.-P. Bouchaud and P. Claudin, Phys. Rev. Lett., 1998, 81, 1841 CrossRef CAS.
- M. O. Robbins, K. Kremer and G. S. Grest, J. Chem. Phys., 1988, 88, 3286 CrossRef CAS.
- V. S. K. Balagurusamy, G. Ungar, V. Percec and G. Johansson, J. Am. Chem. Soc., 1997, 119, 1539 CrossRef CAS.
- S. Chanpuriya, K. Kim, J. Zhang, S. Lee, A. Arora, K. D. Dorfman, K. T. Delaney, G. H. Fredrickson and F. S. Bates, ACS Nano, 2016, 10, 4961 CrossRef CAS PubMed.
- X. Zeng, G. Ungar, Y. Liu, V. Percec, A. E. Dulcey and J. K. Hobbs, Nature, 2004, 428, 157 CrossRef CAS PubMed.
- S. Fischer, A. Exner, K. Zielske, J. Perlich, S. Deloudi, W. Steurer, P. Lindner and S. Förster, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 1810 CrossRef CAS PubMed.
- M. Liu, Y. Qiang, W. Li, F. Qiu and A.-C. Shi, ACS Macro Lett., 2016, 5, 1167 CrossRef CAS.
- T. M. Gillard, S. Lee and F. S. Bates, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 5167 CrossRef CAS PubMed.
- M. W. Schulze, R. M. Lewis III, J. H. Lettow, R. J. Hickey, T. M. Gillard, M. A. Hillmyer and F. S. Bates, Phys. Rev. Lett., 2017, 118, 207801 CrossRef PubMed.
- K. Yue, M. Huang, R. L. Marson, J. He, J. Huang, Z. Zhou, J. Wang, C. Liu, X. Yan, K. Wu, Z. Guo, H. Liu, W. Zhang, P. Ni, C. Wesdemiotis, W.-B. Zhang, S. C. Glotzer and S. Z. D. Cheng, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 14195 CrossRef CAS PubMed.
- S. A. Kim, K.-J. Jeong, A. Yethiraj and M. K. Mahanthappa, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 4072 CrossRef CAS PubMed.
- C. N. Likos, H. Löwen, M. Watzlawek, B. Abbas, O. Jucknischke, J. Allgaier and D. Richter, Phys. Rev. Lett., 1998, 80, 4450 CrossRef CAS.
- G. Malescio and G. Pellicane, Nat. Mater., 2003, 2, 97 CrossRef CAS PubMed.
- J. P. Pàmies, A. Cacciuto and D. Frenkel, J. Chem. Phys., 2009, 131, 044514 CrossRef PubMed.
- T. Dotera, T. Oshiro and P. Ziherl, Nature, 2014, 506, 208 CrossRef CAS PubMed.
- P. Ziherl and R. D. Kamien, Phys. Rev. Lett., 2000, 85, 3528 CrossRef CAS PubMed.
- J. Riest, L. Athanasopoulou, S. A. Egorov, C. N. Likos and P. Ziherl, Sci. Rep., 2015, 5, 15854 CrossRef PubMed.
- B. Widom and J. S. Rowlinson, J. Chem. Phys., 1970, 52, 1670 CrossRef CAS.
- C. Ruscher, J. Baschnagel and J. Farago, EPL, 2015, 112, 66003 CrossRef.
- L. Athanasopoulou and P. Ziherl, Soft Matter, 2017, 13, 1463 RSC.
- D. A. Young and B. J. Alder, Phys. Rev. Lett., 1977, 38, 1213 CrossRef CAS.
- W. Klein, H. Gould, R. A. Ramos, I. Clejan and A. I. Mel’cuk, Physica A, 1994, 205, 738 CrossRef.
- E. A. Jagla, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58, 1478 CrossRef CAS.
- F. D. Murhaghan, Proc. Natl. Acad. Sci. U. S. A., 1944, 30, 245 Search PubMed.
- P. A. Egelstaff and B. Widom, J. Chem. Phys., 1970, 53, 2667 CrossRef CAS.
- K. Brakke, Exp. Math., 1992, 1, 145 Search PubMed ; Surface Evolver is available at http://www.susqu.edu/facstaff/b/brakke/evolver/evolver.html.
- J. A. Barker, Lattice Theories of the Liquid State, Pergamon Press, London, 1963 Search PubMed.
- E. Kabliman, A. V. Ruban, P. Blaha, O. Peil and K. Schwarz, Appl. Sci., 2012, 2, 654 CrossRef CAS.
- Within the range of indentations covered in Fig. 1, drops in the DC lattice are in contact with 4 nearest neighbors but at large h/R* they are also in contact with the 12 next-nearest neighbors. At Ψ = 0.01 and ω = 1, this happens at h/R* ≳ 0.3.
- M.-D. Lacasse, G. S. Grest and D. Levine, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 54, 5436 CrossRef CAS.
- R. Höhler and S. Cohen-Addad, Soft Matter, 2017, 13, 1371 RSC.
- P. Bolhuis and D. Frenkel, Phys. Rev. Lett., 1994, 72, 2211 CrossRef CAS PubMed.
- P. Bolhuis and D. Frenkel, J. Phys.: Condens. Matter, 1997, 9, 381 CrossRef CAS.
- D. Frenkel and B. Smit, Understanding Molecular Simulation, Academic Press, London, 2002 Search PubMed.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, Oxford, 2003 Search PubMed.
- A. Milchev, J. P. Wittmer, P. van der Schoot and D. Landau, Europhys. Lett., 2001, 54, 58 CrossRef CAS.
- V. A. Ivanov, E. A. An, L. A. Spirin, M. R. Stukan, M. Müller, W. Paul and K. Binder, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 026702 CrossRef CAS PubMed.
- F. Lo Verso, A. Z. Panagiotopoulos and C. N. Likos, Faraday Discuss., 2010, 144, 143 RSC.
- C. Koch, A. Z. Panagiotopoulos, F. Lo Verso and C. N. Likos, Soft Matter, 2013, 9, 7424 RSC.
- R. A. Brady, N. J. Brooks, P. Cicuta and L. Di Michele, Nano Lett., 2017, 17, 3276 CrossRef CAS PubMed.
- J. M. Kincaid, G. Stell and E. Goldmark, J. Chem. Phys., 1976, 65, 2172 CrossRef CAS.
- G. Franzese, G. Malescio, A. Skibinsky, S. V. Buldyrev and H. E. Stanley, Nature, 2001, 409, 692 CrossRef CAS PubMed.
- K. Dawson, G. Foffi, M. Fuchs, W. Götze, F. Sciortino, M. Sperl, P. Tartaglia, T. Voigtmann and E. Zaccarelli, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 63, 011401 CrossRef PubMed.
- A. Skibinsky, S. V. Buldyrev, A. Scala, S. Havlin and H. E. Stanley, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, 2664 CrossRef CAS.
- E. A. Jagla, J. Chem. Phys., 1999, 111, 8980 CrossRef CAS.
- P. Kumar, S. V. Buldyrev, F. Sciortino, E. Zaccarelli and H. E. Stanley, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 021501 CrossRef PubMed.
- B. M. Mladek, G. Kahl and C. N. Likos, Phys. Rev. Lett., 2008, 100, 028301 CrossRef PubMed.
- N. Osterman, D. Babič, I. Poberaj, J. Dobnikar and P. Ziherl, Phys. Rev. Lett., 2007, 99, 248301 CrossRef CAS PubMed.
- P. J. Camp, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 061506 CrossRef PubMed.
- D. Vlassopoulos and M. Cloitre, Curr. Opin. Colloid Interface Sci., 2014, 19, 561 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sm00293b |
| This journal is © The Royal Society of Chemistry 2018 |