Cholesteric ordering predicted using a coarse-grained polymeric model with helical interactions†
Abstract
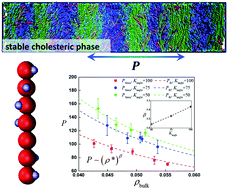
The understanding of cholesteric liquid crystals at a molecular level is challenging. Limited insights are available to bridge between molecular structures and macroscopic chiral organization. In the present study, we introduce a novel coarse-grained (CG) molecular model, which is represented by flexible chain particles with helical interactions (FCh), to study the liquid crystalline phase behavior of cholesteric molecules such as double strand DNA and α-helix polypeptides using molecular dynamics (MD) simulations. The isotropic–cholesteric phase transitions of FCh molecules were simulated for varying chain flexibilities. A wall confinement was used to break the periodicity along the cholesteric helix director in order to predict the equilibrium cholesteric pitch. The left-handed cholesteric phase was shown for FCh molecules with right-handed chiral interactions, and a spatially inhomogeneous distribution of the nematic order parameter profile was observed in cholesteric phases. It was found that the chain flexibility plays an important role in determining the macroscopic cholesteric pitch and the structure of the cholesteric liquid crystal phase. The simulations provide insight into the relationship between microscopic molecular characteristics and the macroscopic phase behavior.


 Please wait while we load your content...
Please wait while we load your content...