Shear thinning in non-Brownian suspensions
Abstract
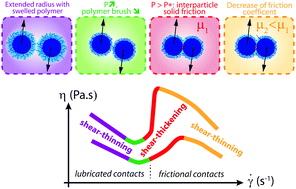
We study the flow of suspensions of non-Brownian particles dispersed into a Newtonian solvent. Combining capillary rheometry and conventional rheometry, we evidence a succession of two shear thinning regimes separated by a shear thickening one. Through X-ray radiography measurements, we show that during each of those regimes, the flow remains homogeneous and does not involve particle migration. Using a quartz-tuning fork based atomic force microscope, we measure the repulsive force profile and the microscopic friction coefficient μ between two particles immersed into the solvent, as a function of normal load. Coupling measurements from those three techniques, we propose that (1) the first shear-thinning regime at low shear rates occurs for a lubricated rheology and can be interpreted as a decrease of the effective volume fraction under increasing particle pressures, due to short-ranged repulsive forces and (2) the second shear thinning regime after the shear-thickening transition occurs for a frictional rheology and can be interpreted as stemming from a decrease of the microscopic friction coefficient at large normal load.


 Please wait while we load your content...
Please wait while we load your content...