Abstract
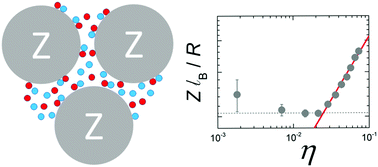
Individual colloids often carry a charge as a result of the dissociation (or adsorption) of weakly-ionized surface groups. The magnitude depends on the precise chemical environment surrounding a particle, which in a concentrated dispersion is a function of the colloid packing fraction η. Theoretical studies have suggested that the effective charge Zeff in regulated systems could, in general, decrease with increasing η. We test this hypothesis for nonpolar dispersions by determining Zeff(η) over a wide range of packing fractions (10−5 ≤ η ≤ 0.3) using a combination of small-angle X-ray scattering and electrophoretic mobility measurements. All dispersions remain entirely in the fluid phase regime. We find a complex dependence of the particle charge as a function of the packing fraction, with Zeff initially decreasing at low concentrations before finally increasing at high η. We attribute the non-monotonic density dependence to a crossover from concentration-independent screening at low η, to a high packing fraction regime in which counterions outnumber salt ions and electrostatic screening becomes η-dependent. The efficiency of charge stabilization at high concentrations may explain the unusually high stability of concentrated nanoparticle dispersions which has been reported.


 Please wait while we load your content...
Please wait while we load your content...