Drop on a bent fibre†
Abstract
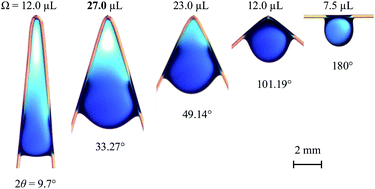
Inspired by the huge droplets attached on cypress tree leaf tips after rain, we find that a bent fibre can hold significantly more water in the corner than a horizontally placed fibre (typically up to three times or more). The maximum volume of the liquid that can be trapped is remarkably affected by the bending angle of the fibre and surface tension of the liquid. We experimentally find the optimal included angle (∼36°) that holds the most water. Analytical and semi-empirical models are developed to explain these counter-intuitive experimental observations and predict the optimal angle. The data and models could be useful for designing microfluidic and fog harvesting devices.


 Please wait while we load your content...
Please wait while we load your content...