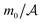Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Nonadditive interactions and phase transitions in strongly confined colloidal systems†
Oleg A.
Vasilyev
 *ab,
S.
Dietrich
*ab and
Svyatoslav
Kondrat
*ab,
S.
Dietrich
*ab and
Svyatoslav
Kondrat
 *cd
*cd
aMax-Planck-Institut für Intelligente Systeme, Heisenbergstraße 3, D-70569 Stuttgart, Germany. E-mail: dietrich@is.mpg.de
bIV. Institute für Theoretische Physik, Universität Stuttgart, Pfaffenwaldring 57, D-70569 Stuttgart, Germany
cInstitute for Computational Physics, University of Stuttgart, Allmandring 3, 70569 Stuttgart, Germany
dInstitute of Physical Chemistry, Polish Academy of Sciences, Kasprzaka 44/52, 01-224 Warsaw, Poland. E-mail: svyatoslav.kondrat@gmail.com; skondrat@ichf.edu.pl
First published on 21st December 2017
Abstract
The behaviour of colloids can be controlled effectively by tuning the solvent-mediated interactions among them. An extensively studied example is the temperature-induced aggregation of suspended colloids close to the consolute point of their binary solvent. Here, using mean field theory and Monte Carlo simulations, we study the behaviour of colloids confined to a narrow slit containing a nearly-critical binary liquid mixture. We found that the effective interactions in this system are highly non-additive. In particular, the effective interactions among the colloids can be a few times stronger than the corresponding sum of the effective pair potentials. Inter alia, this non-additivity manifests itself in the phase behaviour of confined colloids, which depends sensitively on the slit width and temperature. In addition, we demonstrate the possibility of a first-order bridging transition between colloids confined to a slit and suspended in a phase-separated fluid well below the critical point of the solvent and at its critical composition in the bulk. This transition is accompanied by a remarkably large hysteresis loop, in which the force between the colloids varies by two orders of magnitude.
Introduction
Colloids attract increasing attention from scientists and engineers as models for atoms and molecules1 and due to numerous technological applications in the food industry,2 medicine,3 and other fields.4–7 The behaviour of a colloidal suspension can be effectively controlled by tuning the properties of its solvent, such as the concentration, temperature, and composition. An outstanding example is the coagulation of colloids close to the critical point of the solvent, which gives rise to the so-called critical Casimir forces induced by order parameter fluctuations.8–22 Correspondingly, the phase behaviour of such a colloidal system exhibits well-defined colloidal, liquid and gas phases. Additionally, a number of crystalline phases23,24 and glassy states25 have been identified.As a result of confinement, most physical processes deviate from their bulk behaviour, and may exhibit even new physical phenomena. The corresponding plethora of phenomena includes, e.g., unusual drying transitions26 and freezing27,28 of confined water, an anomalous increase of capacitance in subnanometer pores,29,30 a remarkable long-ranged repulsion between confined van der Waals dimers,31etc. As we shall report, remarkable phenomena emerge also in strongly confined colloidal systems. Such systems have attracted much attention recently,32–35 in particular as models to study the behaviour of particles in (quasi) two spatial dimensions.36,37 Previous experimental and theoretical studies have focused on such systems with short- or long-ranged repulsive interactions in the context of the Kosterlitz–Thouless transition.38–43 However, identical colloids in a narrow slit filled by a nearly critical solvent acquire strong long-ranged attractive interactions, which can be manipulated by minute changes of temperature or solvent composition. This allows one to study two-dimensional systems with tunable attractive interactions, and it may open up the door for novel types of two-dimensional photonic crystals to serve as sensing devices.44
The strong colloid–colloid interactions near the consolute point of a solvent are due to an increased correlation length of the solvent and due to modifications of its order parameter fluctuations caused by the presence of the colloids (for instance concentration fluctuations in a binary liquid mixture or density fluctuations in a simple fluid).45,46 By analogy with the quantum Casimir effect, where the confinement of zero-point fluctuations of the electromagnetic fields leads to a measurable effective force between the confining surfaces,47 the solvent-mediated force close to the consolute point of the solvent is called a critical Casimir force. Similar to their quantum-mechanical analogues, the critical Casimir interactions can be attractive or repulsive depending on the boundary conditions, viz. the force is attractive for like and repulsive for unlike boundaries.48 For a binary liquid mixture, the two types of boundary conditions (say ‘+’ and ‘−’) are determined by the preference of the surfaces for one of the two solvent species. Since confined near-critical binary liquid mixtures belong to the Ising bulk universality class and to the so-called normal surface universality class, such surface preferences map onto fixing the boundary spins to the values +1 or −1.49,50
In the aforementioned context of the collective behaviour of the colloids, an important feature of critical Casimir forces is their non-additivity. Previous theoretical studies have focused on non-additivity in systems consisting of three colloids51 and of two colloids near a wall,52 using a numerical mean field approach.53,54 In a very recent experimental study55 the non-additivity of critical Casimir interactions has been observed for three colloidal particles. The measured colloid–colloid Casimir potential was modified by the presence of a third colloid, as compared to the system with two colloids only. In these systems, however, the contribution due to non-additivity constitutes less than 20% of the total Casimir interaction, which is difficult to capture experimentally or numerically due to potentially significant inaccuracies.
Here, we shall demonstrate that the critical Casimir interactions in a confined colloidal suspension are highly non-additive. It is evident that if such interactions were additive, then the lateral force between the colloids would be unaffected by the presence of the slit walls. We shall show, however, that this is not only not the case, but that the non-additivity can strongly change the colloid–colloid interactions. This non-additivity gives rise to a sensitive slit-width dependent phase behaviour of the confined colloids, which can be used to probe and visualize the non-additivity of critical Casimir interactions experimentally.
While in the critical region of the solvent the colloid–colloid interactions are determined by strong long-ranged correlations of the fluid, a different physical mechanism takes place below the critical point of the solvent, where two distinct homogeneous phases can coexist. For example, in the case of a binary mixture of species A and B, these phases are rich in A and B; or they are the liquid and gas phases in the case of a simple fluid. In a system in which one of these phases is thermodynamically favoured in the bulk, it is possible that the other phase is preferred by the colloidal surfaces. In this case a wetting layer forms around a single colloid, which may extend to form a capillary bridge between two (or more) colloids.56–59 Such capillary bridges may undergo so-called bridging transitions and give rise to strong capillary forces, which can be used to construct temperature-controlled colloidal networks and microstructures.60 Here, we shall show that in a confined colloidal system the capillary forces and bridging transitions can be observed even in the case of no preference in the corresponding unconfined system and that they can be effectively controlled by the confinement.
Solvent-mediated interactions between confined colloids
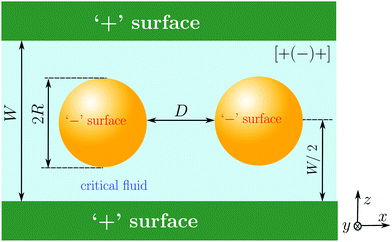
Although we do not restrict our considerations to the critical region of the solvent, it will be convenient to discuss the solvent-mediated forces comprehensively in terms of scaling functions. For two identical colloids centered in the symmetry plane of a slit (see Fig. 1), we represent the force between the colloids as reported in ref. 61 and 62 (for the notations see Fig. 1)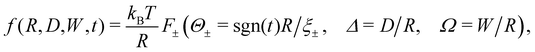 | (1) |
Integrating f over the colloid–colloid separation gives the critical Casimir potential ϕ, which likewise can be presented in the scaling form
ϕ(R,D,W,t) = kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) Φ±(Θ±,Δ,Ω). Φ±(Θ±,Δ,Ω). | (2) |
In the limit Ω = W/R → ∞ one might expect that the scaling functions F and Φ reduce to the scaling functions for two colloids in a bulk critical fluid, i.e., F(Θ,Δ,Ω = ∞) = Fbulk(Θ,Δ) and Φ(Θ,Δ,Ω = ∞) = Φbulk(Θ,Δ), which have been extensively studied in the literature.19,61,62,64 Therefore, the bulk scaling functions lend themselves as a reference to compare with, and deviations from Fbulk and Φbulk serve as a measure of non-additivity, as shown in previous analyses.51,52,55
We shall use mean field theory (MFT) and Monte Carlo (MC) simulations (of the Ising model) in order to calculate the scaling functions F and Φ for the system shown in Fig. 1. We consider a generic symmetric configuration, [α(β)α], where α and β (= ‘+’ or ‘−’) denote the boundary conditions at the surface of the slit walls and of the two identical colloids, respectively. Such symmetric configurations can be realized experimentally by placing colloids into a binary liquid mixture (e.g., water/lutidine) confined between parallel glass plates.65–67 First, we shall study how such a narrow slit confinement alters the bulk critical Casimir interactions between the colloids, and thus manifests non-additivity. Then, we shall consider two important ramifications resulting from the confinement and from non-additivity.
Reduction, enhancement, and screening of colloidal interactions by confinement
 | ||
| Fig. 2 The effect of confinement Ω = W/R on critical Casimir interactions between colloids from mean field calculations for the [+(+)+] configuration (Fig. 1). The force scaling function F is plotted versus scaled temperature expressed in terms of the scaling variable Θ = Θ± = sgn(t)R/ξ±(t). F is normalized by the scaling function Fbulk(Θ = 0,Δ) of the critical Casimir force between two colloids in a bulk fluid. The inset shows F as a function of the slit width Ω = W/R; here F is normalized by Fbulk at the given values of Θ and Δ. | ||
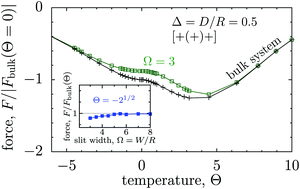
However, the critical Casimir force shows a qualitatively different behaviour for the opposite boundaries of the [+(−)+] configuration (Fig. 3(a and b)). The corresponding scaling function starts to deviate from the scaling function Fbulk in the bulk for Θ = Θ± = R/ξ± = sgn(t)|t|1/2R/ξ±0 ≲ 5. This deviation increases strongly as the scaled temperature Θ decreases towards negative values, i.e., T < Tc (Fig. 3a). Remarkably, upon increasing the slit width, the scaling function F− does not approach F−bulk, unlike in all other cases (see the inset in Fig. 2 as well as Fig. 3b).
 | ||
Fig. 3 The effect of confinement Ω = W/R on critical Casimir interactions between colloids from mean field calculations. (a) Force scaling functions F versus scaled temperature expressed in terms of the scaling variable Θ = Θ± = sgn(t)R/ξ±(t). F is normalized to the scaling function Fbulk(Θ = 0, Δ) of the critical Casimir force between two colloids in a bulk fluid. (b) F is shown as a function of the slit width Ω = W/R and is normalized to Fbulk at given Θ and Δ. For Θ < 0 and Ω → ∞ the scaling function F− does not approach F−bulk (i.e., the blue line does not approach 1). (c) The order parameter φ in the middle of the slit at a distance 2R outside the colloids (in the x direction, see Fig. 1) as a function of temperature for various slit widths; φ is normalized to the amplitude 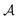 of the order parameter in the bulk system without colloids. In panels (a)–(c) the surface-to-surface distance between the colloids is Δ = D/R = 0.5. (d) Casimir force scaling functions versus surface-to-surface distance Δ = D/R between the colloids. The force is normalized to the amplitude of the order parameter in the bulk system without colloids. In panels (a)–(c) the surface-to-surface distance between the colloids is Δ = D/R = 0.5. (d) Casimir force scaling functions versus surface-to-surface distance Δ = D/R between the colloids. The force is normalized to the amplitude 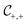 of the critical Casimir force at Tc for a slit with (+,+) boundary conditions. The case Ω = ∞ has been obtained in a bulk system (i.e., no slit walls) by applying a weak external bulk field, with the sign opposite to the boundary conditions on the colloid surfaces, in order to mimic the presence of the slit walls infinitely far from the colloids (see the main text and Methods). This scaling function practically coincides with the scaling function calculated for Ω = 10. In all plots the centers of the colloids are located in the symmetry plane of the slit (Fig. 1). of the critical Casimir force at Tc for a slit with (+,+) boundary conditions. The case Ω = ∞ has been obtained in a bulk system (i.e., no slit walls) by applying a weak external bulk field, with the sign opposite to the boundary conditions on the colloid surfaces, in order to mimic the presence of the slit walls infinitely far from the colloids (see the main text and Methods). This scaling function practically coincides with the scaling function calculated for Ω = 10. In all plots the centers of the colloids are located in the symmetry plane of the slit (Fig. 1). | ||
Although at first glance this behaviour might seem surprising, it has a simple explanation. Indeed, for T < Tc (i.e., t < 0) there are two stable states with the order parameter values 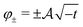 , both of which minimize the bulk free energy in the limits h → ±0, respectively, where h is the external bulk field conjugate to the order parameter (see h in eqn (3) in Methods), and
, both of which minimize the bulk free energy in the limits h → ±0, respectively, where h is the external bulk field conjugate to the order parameter (see h in eqn (3) in Methods), and 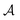 is the amplitude of the bulk order parameter. In the unconfined system (i.e., free boundary conditions at infinity), the value of the order parameter far from the colloids (φ+ or φ−) follows the preference of the colloid surfaces, while in confinement that value is set by the slit walls. This is borne out by Fig. 3c, where we plot the order parameter in the middle of the slit at a distance 2R outside the colloids (along the x axis, see Fig. 1). For Θ ≲ −3, the curves for Ω = W/R = 3 and Ω = 10 practically coincide, while for the unconfined (bulk) system the order parameter has the opposite sign and is consistent with the boundary conditions at the colloid surfaces. Correspondingly, the forces in wide slits (Ω → ∞) and in the unconfined bulk system differ substantially in that the wide slits generate the presence of a +/− interface.
is the amplitude of the bulk order parameter. In the unconfined system (i.e., free boundary conditions at infinity), the value of the order parameter far from the colloids (φ+ or φ−) follows the preference of the colloid surfaces, while in confinement that value is set by the slit walls. This is borne out by Fig. 3c, where we plot the order parameter in the middle of the slit at a distance 2R outside the colloids (along the x axis, see Fig. 1). For Θ ≲ −3, the curves for Ω = W/R = 3 and Ω = 10 practically coincide, while for the unconfined (bulk) system the order parameter has the opposite sign and is consistent with the boundary conditions at the colloid surfaces. Correspondingly, the forces in wide slits (Ω → ∞) and in the unconfined bulk system differ substantially in that the wide slits generate the presence of a +/− interface.
Fig. 3(a) and (b) show that for the [+(−)+] configuration the critical Casimir force between colloids is stronger for stronger confinement. However, this only holds if the distance D between the colloids is small. Indeed, Fig. 3d demonstrates that for large D (≳ 2R) the force is significantly larger for wider slits. In other words, confinement screens the critical Casimir interactions at large colloid–colloid separations. This surprising behaviour can be related to the formation of an order-parameter ‘bridge’ linking two colloids at small distances (Fig. S1 in the ESI,† see, cf., also Fig. 6a).56–58,68 Pulling the colloids away from each other will eventually cause this bridge to break at a certain distance Dbridge. Without the bridge the order parameter coronas around each colloid overlap barely and hence the interaction between the colloids is much weaker. Dbridge decreases for narrowing the slit because the slit walls are opposite to the colloids and enforce the bridge to break. Therefore, for thin slits the decrease of the force occurs at small D, while the force remains strong for slits wide enough to keep the bridge intact. For instance, for Θ− = −2 in Fig. 3d we find Dbridge/R ≈ 2 for Ω = W/R = 3, while Dbridge/R ≳ 4 for Ω = 10 (not shown).
Interestingly, for wide slits and Θ < 0 the force between the colloids practically coincides with the force obtained for the unconfined systems upon applying a weak external bulk field h > 0 (Ω = 10 and Ω = ∞, respectively, in Fig. 3d). This is because in this case the bulk field sets the value of the order parameter far from the colloids to be opposite in sign to the boundary conditions at the colloid surfaces. This leads to the formation of order-parameter bridges connecting the two colloids and hence to quantitatively comparable forces.
We shall discuss ‘bridging’ and bridging transitions in more detail below. Before, however, we analyze how our MFT results compare with the corresponding Monte Carlo simulation data.
We emphasize that due to computational limitations the systems studied via MC simulations had to be relatively small. For instance, the diameter of the colloids was 11 lattice constants (corresponding to 11 spins) and the distance between the surfaces of two colloids in some cases was as small as just two spins. (Larger distances up to 30 spins have also been considered.) Such small systems are expected to show some degree of non-universality, which is the case also for our MC results (unlike the present version of MFT, which focuses on the universal behaviour). It seems that there is no alternative for removing this non-universal contribution other than by simulating larger systems. Therefore, we present our unprocessed simulation data. However, by comparing the MC results for various system sizes, we have checked that these data are dominated by the universal contribution (see Fig. S3 and Section S2A in the ESI†).
In view of the above discussion, nevertheless the MFT and MC results are consistent with each other. Fig. 4(a) shows that the depth of the Casimir potential can reach values as large as −20kBT, which is more than 6 times stronger than the maximum of −3kBT obtained in the bulk system. Remarkably, for low temperatures (T < Tc) the Casimir interactions are stronger for wider slits, while narrow slits provide stronger interactions close to Tc (Θ ≪ 1). Similarly, for small colloid–colloid separations (D ≲ R), the interactions are stronger for thinner slits, but thin slits screen the Casimir interactions more effectively if D is large (Fig. 4b). This is in line with the corresponding MFT results (Fig. 3d) and can be related to the breaking of a bridge formed between colloids as the distance between them increases (Fig. S1 and S4 in the ESI†).
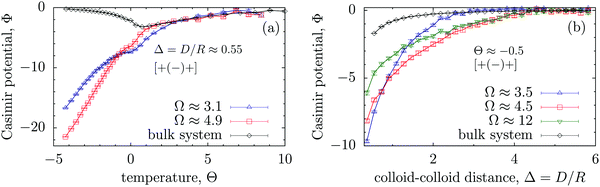 | ||
| Fig. 4 Effect of confinement Ω = W/R on the critical Casimir interaction potential between colloids from Monte Carlo simulations. (a) The universal scaling function Φ of the critical Casimir potential is shown as a function of scaled temperature, expressed in terms of the scaling variable Θ = Θ± = sgn(t)R/ξ±(t), and (b) as a function of Δ = D/R. In all plots the centres of the colloids are located on the symmetry plane of the slit (Fig. 1). Note that Φ for the wide slit (Ω = 12) differs from Φbulk, in accord with the MFT results (Fig. 3b and d). | ||
Phase behaviour of confined colloids
In the following we use the critical Casimir potential obtained from our Monte Carlo simulations in order to study the phase behaviour of confined colloids. We consider only narrow confinements, in which colloids position themselves in the symmetry plane of a slit (Fig. S6 in the ESI†). In order to calculate the phase diagram of such an effectively two-dimensional system, we have used the random phase approximation (RPA) in two dimensions (see Methods and Section S3 in the ESI†). We note that within this approach we take into account the non-additivity due to the slit walls, but we ignore the many-body Casimir interactions among the colloids. Although the latter contribution is expected to be small,51,52,55 it will nevertheless be interesting to analyse such effects in future studies.As an example, we consider colloids of radius R = 250 nm (ref. 17) suspended in a 3-methyl-pyridine (3MP)/heavy water mixture, which has the bulk critical temperature Tc ≈ 312 K and the correlation length amplitude ξ+0 ≈ 1.5 nm.18,19 We consider charged colloids so that the effective hard disk radius is σ ≈ 1.05R due to a short-ranged electrostatic repulsion (Section S3 in the ESI†). The resulting phase diagram is shown in Fig. 5 in the plane of the two-dimensional colloidal packing fraction η and the deviation ΔT = T − Tc from the consolute point Tc of the solvent in bulk. As in d = 3, there is a region in the phase diagram where the colloidal gas phase and the colloidal liquid phase coexist. This region shrinks as ΔT increases and ends in a colloidal critical point (ηcc, ΔTcc = Tcc − Tc). The colloidal critical temperature deviation ΔTcc increases for narrower slits because confinement enhances the critical Casimir interactions (for small colloid–colloid separations, see Fig. 4b and Fig. S5 in the ESI†). Screening of interactions at large separations is not sufficient to significantly change this behaviour; however, it generates only a relatively moderate dependence of the colloidal phase diagram on the slit width. Nonetheless, taking into account that current cooler/heater systems can control temperature with a precision of about 2 mK (see, e.g., ref. 55), this slit-width dependence of the colloidal phase diagram appears to be experimentally well accessible.
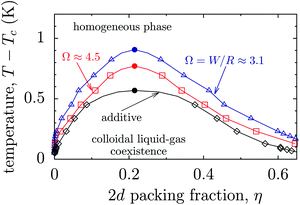 | ||
| Fig. 5 Phase diagram of colloids confined to a narrow slit containing a near-critical solvent. The diagram is drawn in the plane of the two-dimensional (2d) packing fraction η of the colloids and the temperature deviation ΔT = T − Tc from the bulk critical point of the solvent, for two values of the slit width Ω = W/R. The lines are guides to the eyes and the filled circles indicate the approximate locations of the colloidal critical points (Fig. S7 in the ESI†). The phase diagrams (symbols) have been calculated using the random phase approximation in two dimensions. The colloid–colloid interaction potentials have been obtained from the three-dimensional Monte Carlo simulations of the Ising model. The diagrams are calculated for colloids of radius R = 250 nm, while the hard disk radius is σ = 1.05R, taking into account the short-ranged repulsive electrostatic interactions between actual charged colloids (see Methods and Section S3 in ESI†). The solid line and the diamonds denote the phase diagram of a hypothetical system with the bulk critical Casimir potential taken for the effective colloid–colloid interaction, which would be realized for the slit confinement if the interactions were additive. | ||
It is instructive to estimate the effect of non-additivity on the colloidal phase diagram. To this end we recall that if the interactions were additive, the lateral interactions between colloids would not be altered by the presence of the slit walls. Thus, we take the critical Casimir potential of the bulk (unconfined) system and calculate the corresponding two-dimensional phase diagram. (Physically this means that the colloids should be confined to the midplane by alternative means, for instance by optical tweezers; to which extent this can be implemented experimentally has to be tested.) For the 3MP/heavy water mixture discussed above, we find that the colloidal critical point of this system would be at ΔTcc ≈ 0.53 K, which is significantly closer to the bulk critical point of the solvent (i.e., ΔT = 0) than the system of colloids in the actual slit confinement (see Ω = 3.1 and 4.5 in Fig. 5).
We thus conclude that confined colloids present a simple and convenient system for probing experimentally the occurrence of non-additivity of critical Casimir interactions via measuring the slit-width dependence of the colloidal phase diagram.
Bridging transitions for confined colloids
Fig. 3d and 4b show that for T < Tc the colloid–colloid interactions decay rapidly as the separation between them increases. We have related this behaviour to the breaking of a bridge formed between the colloids at small separations (Fig. S1 and S4 in the ESI†). Such capillary bridges in near-critical fluids have been previously investigated both theoretically56–59,70–73 and experimentally74 for colloids in bulk systems56–59,72–74 and for inhomogeneous slits without colloids.70,71 Here, motivated by the remarkable behaviour of the force (Fig. 3d and 4b), we study the temperature-induced bridge formation between two colloids in a strong slit confinement using mean field theory and Monte Carlo simulations of the Ising model (see Methods).Our mean field calculations predict that the formation and the breaking of bridges can occur via first-order (discontinuous) phase transitions. Fig. 6(a) shows that the configurations with and without bridge can coexist, i.e., both configurations can be stable or metastable at the same temperature, slit width, and colloid–colloid separation.
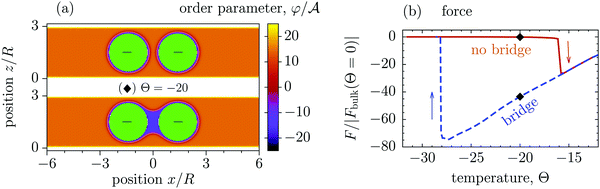 | ||
Fig. 6 Bridging transition and hysteresis for two confined colloids corresponding to the [+(−)+] configuration obtained from mean field theory. (a) Normalized order parameter (OP) distribution for two coexisting configurations with and without a bridge between two identical colloids. The OP is normalized by its amplitude 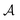 in the bulk (unconfined) system with no colloids. The same parameters are used in the top and in the bottom panel, viz. the slit width W = 3R, where R is the colloidal radius, the surface-to-surface distance D = 0.8R between the colloids, and the temperature scaling variable Θ = −20. (b) The normalized attractive force between two colloids as a function of scaled temperature Θ = sgn(t)R/ξ(t). The arrows indicate the directions in the hysteresis loop, and the black diamonds denote the temperature used for the plots in (a). Concerning the formation and breaking of a bridge along the hysteresis loop, see Supplementary Video (ESI†). Note that within MFT the discontinuity of the force upon a bridging transition corresponds to a break in slope of the effective potential due to the crossing of the free energy branches for the bridge and no-bridge states. Concerning the locus of the bridging transition see the corresponding discussion in the main text. in the bulk (unconfined) system with no colloids. The same parameters are used in the top and in the bottom panel, viz. the slit width W = 3R, where R is the colloidal radius, the surface-to-surface distance D = 0.8R between the colloids, and the temperature scaling variable Θ = −20. (b) The normalized attractive force between two colloids as a function of scaled temperature Θ = sgn(t)R/ξ(t). The arrows indicate the directions in the hysteresis loop, and the black diamonds denote the temperature used for the plots in (a). Concerning the formation and breaking of a bridge along the hysteresis loop, see Supplementary Video (ESI†). Note that within MFT the discontinuity of the force upon a bridging transition corresponds to a break in slope of the effective potential due to the crossing of the free energy branches for the bridge and no-bridge states. Concerning the locus of the bridging transition see the corresponding discussion in the main text. | ||
In this context, a remarkably large hysteretic loop of the solvent-mediated force is observed as a function of temperature (Fig. 6b). This hysteresis occurs because the system follows different metastable branches, with and without bridges, as temperature increases and decreases. The force is very strong if there is a bridge between the colloids (almost two orders of magnitude stronger than the force at the critical point), but it practically vanishes if the bridge ruptures. Interestingly, the free energies of these two states are surprisingly close to each other (Fig. S2 in the ESI†), so that it is even difficult to determine the transition point (as the intersection of the free energy branches) with certainty, and hence it is not shown in Fig. 6b. However, this also means that the bridge and no-bridge configurations are de facto equally stable and exhibit quasi-coexistence in a wide range of temperatures. Taking as an example the 3-methyl-pyridine/heavy water mixture (critical point Tc ≈ 312 K and correlation length amplitude ξ+0 ≈ 1.5 nm, see ref. 18 and 19), and colloids with 0.5 μm in diameter, from Fig. 6b we roughly estimate the size of this coexistence region to be 0.74 K, starting at approximately 0.36 K below Tc. We regard this to be experimentally accessible. (Note, however, that this estimate follows from MFT, accounting for fluctuations is expected to modify the size and the location of the coexistence region.)
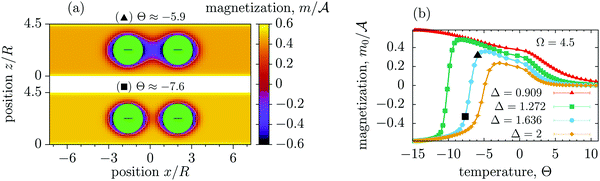
Although we do observe the formation of bridges in our MC simulations (Fig. 7a and Fig. S4 in ESI†), we have not found sufficiently strong arguments to identify the bridging transition. In order to check this possibility, we have studied – in Ising language – the magnetization m0 at the mid-point between the two colloids, which can serve as an order parameter distinguishing the bridge and no-bridge states (m0 > 0 in the no-bridge and m0 < 0 in the bridge state for the [+(−)+] configuration). In the case of a first-order transition, m0 should jump at the transition. However, our simulations suggest that m0 varies continuously as a function of Θ (Fig. 7b), which implies a continuous transformation between the bridge and no-bridge configurations. This is likely due to the fact that the colloids in our simulations are too small to accomplish the transition. Indeed, our colloids have a radius of 5.5 to 7.5 lattice constants, which roughly corresponds to a few nanometers and thus is comparable with the correlation length at the suspected transition. This means that even thermal fluctuations can render a metastable bridge state unstable. In ref. 72 and 73 it has been demonstrated that for a bulk system with a square-well fluid–fluid interaction potential (with a range of 1.5a, where a is the diameter of the molecules of the solvent) the bridging transitions can only take place if the colloidal radius is larger than ≈10a, which translates to roughly 10 lattice constants in the simulated Ising model. With the currently available computational resources we have not been able to simulate such large systems. We leave this task for future studies.
Finally, we point out that, according to the line of arguments provided by ref. 56, the bridging transition between spheres involves only a quasi-zero dimensional volume of ordering degrees of freedom, which smears out this first-order phase transition. This finite size effect has to be taken into account for the interpretation of MC data for large systems.
Conclusions
Using mean field theory and Monte Carlo simulations of the Ising model, we have found a remarkably strong non-additivity of critical Casimir interactions in confined colloidal suspensions. This follows from noting that if the assumption of additivity were correct, the lateral interactions between colloids in a slit would not be affected by the walls. In sharp contrast, however, we have found that for small colloid–colloid separations the critical Casimir interactions can be enhanced through confinement several times over. At larger separations, in contrast, the colloid–colloid interactions are strongly screened as the slit becomes narrower (Fig. 3 and 4).This non-additivity manifests itself in the phase behaviour of confined colloidal suspensions. Similar to a bulk (i.e., unconfined) system, there are liquid-like and gaseous colloidal phases, which can coexist in certain ranges of temperature and colloidal packing fraction. The coexistence region ends in a critical point, which depends sensitively on the slit width and is located far above the critical point of a hypothetical system with additive interactions (Fig. 5). This means that determining the phase diagram of a confined colloidal system provides an indirect but convenient method for probing experimentally the presence of non-additivity of critical Casimir interactions.
An important consequence of confinement and non-additivity is the formation and breaking of capillary bridges between colloids immersed into a solvent at its critical composition. Mean field theory predicts that this process can proceed via a first-order bridging transition, characterized by a remarkably extended hysteresis loop (Fig. 6). Experimentally, the formation of bridges has been observed, e.g., for glass colloids in a water/lutidine mixture close to its two-phase coexistence line.74 However, experiments on bridging transitions are scarce. Our study proposes a convenient setup, with the slit width as a new control parameter, for analyzing such transitions and thereby providing a framework to observe them experimentally.
We have focused here only on a few aspects of the behaviour of confined colloidal systems. Such systems, however, can show a far richer behaviour. For instance, we have discussed colloidal liquid–gas transitions (Fig. 5), but two-dimensional crystalline structures can also form;36,43 they may have potential applications in two-dimensional photonic sensors.44 We have considered the temperature-dependent formation of bridges between confined colloids, but the slit width presents an additional parameter to control the bridges and the bridging transitions. Colloids can also help to detect interface localization/delocalization transitions, predicted for a noncritical fluid in the ordered phase confined between two walls with opposing boundary conditions. Although extensively studied theoretically,75–80 such transitions have not yet been observed experimentally. Our preliminary calculations show that the force acting on a colloid confined in such a system experiences a vivid change when the interface localizes at one of the walls. Therefore this change can serve as an experimental indicator of the localization/delocalization transition.
We thus conclude that confined colloidal systems offer exciting opportunities to study a number of interesting phenomena and have the potential in technological applications. We expect that our results will stimulate future activities in this area, both in basic and applied research.
Methods
Mean field approach
The MFT equilibrium order-parameter profiles have been obtained by minimizing numerically the standard dimensionless Ginzburg–Landau–Wilson (LGW) Hamiltonian in spatial dimension d = 3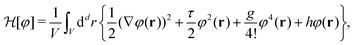 | (3) |
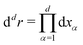 is the d-dimensional volume element, φ(r) is the order parameter (for a binary liquid mixture it is the deviation of the concentration of one species from its critical value), h is the external bulk field conjugate to φ (in the present study mostly taken to be zero, see below), V is the volume accessible to the critical fluid, and the coupling constant g > 0 stabilizes
is the d-dimensional volume element, φ(r) is the order parameter (for a binary liquid mixture it is the deviation of the concentration of one species from its critical value), h is the external bulk field conjugate to φ (in the present study mostly taken to be zero, see below), V is the volume accessible to the critical fluid, and the coupling constant g > 0 stabilizes 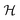 below Tc. Within MFT τ = t/(ξ+0)2 where t = (T − Tc)/Tc is the reduced temperature, and ξ+0 is the amplitude of the bulk correlation length in the disordered phase. Note that we consider here three-dimensional spherical colloids, which form hyper-cylinders in d = 4 for which MFT predicts the correct critical behaviour.
below Tc. Within MFT τ = t/(ξ+0)2 where t = (T − Tc)/Tc is the reduced temperature, and ξ+0 is the amplitude of the bulk correlation length in the disordered phase. Note that we consider here three-dimensional spherical colloids, which form hyper-cylinders in d = 4 for which MFT predicts the correct critical behaviour.
The computational box for the numerical minimization was chosen sufficiently large in the lateral directions in order to ensure that the order parameter (OP) far from the colloids coincides with the OP profile dictated by the slit walls. A surface-to-surface distance of 5R from the colloids of radius R to the sides of the computational box turned out to be sufficient to meet this criterion. The values of the order parameter at these box sides were left free during minimization and there was no surface free energy associated with them due to choosing von Neumann boundary conditions in both lateral directions.
We consider the colloids and the slit walls to belong to the so-called extraordinary (or normal) surface universality class. Accordingly, the order parameter diverges upon approaching such surfaces (see, e.g., ref. 49, 50 and 81). In order to deal with this numerical challenge, we have used a short-distance expansion (see ref. 53 and 82) for calculating the value of the OP at some small distances δ from the surface (we took δ = 0.05R in all calculations). During minimization we kept the OP fixed on all mesh nodes belonging to that surface. This approach has proven to be successful in a number of previous studies.19,51–53,83,84
The critical Casimir force was calculated using the stress tensor method.53 Each colloid was enclosed by an ellipsoidal surface (Si) and the force acting on colloid i was calculated by integrating the stress tensor over Si (Section S1 in the ESI†).
For calculating the curve for Ω = ∞ in Fig. 3d, we have used the ‘−’ boundary condition at the surfaces of both colloids and a weak opposing external bulk field h > 0 (see eqn (3)), in order to mimic the effect of having ‘+’ walls far from the colloids. We checked that the calculated forces are practically indistinguishable for R/ξh ≲ 0.37, where 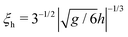 is the correlation length along the critical isotherm within mean field theory. Apart from this aspect we have set the bulk field to zero in all other calculations. (For further details concerning ξh see eqn (4.2) in ref. 62 and Section 4.7 therein, as well as the appendix and the text after eqn (21) in ref. 85.)
is the correlation length along the critical isotherm within mean field theory. Apart from this aspect we have set the bulk field to zero in all other calculations. (For further details concerning ξh see eqn (4.2) in ref. 62 and Section 4.7 therein, as well as the appendix and the text after eqn (21) in ref. 85.)
The hysteresis loop in Fig. 6b has been determined as follows. We first minimized the LGW Hamiltonian for a certain small t just below t = 0, starting from a random OP configuration. Then we used this solution as a starting configuration in a new minimization process for a lower, but still sufficiently small temperature t, as to ensure that the minimizer chooses the required (local) minimum. We continued this procedure until the lowest temperature presented in Fig. 6b was reached. The return path of the loop was obtained similarly by starting from low t < 0, at which there is no metastability; then we increased t stepwise and proceeded as described above.
Monte Carlo simulations
We have considered the standard Ising model with classical spins ±1 located on a cubic lattice, which mimics an incompressible binary mixture with spins corresponding to different species of the mixture. This spin model is a representative of the d = 3 Ising universality class, pertinent to the vicinity of the consolute critical point of the binary liquid mixture. For this model the value of the inverse critical temperature is βc = 1/kBTc = 0.2216544(3) and amplitudes of the correlation length for the low- and high-temperature regions are ξ−0 = 0.243(1) and ξ+0 = 0.501(2), respectively, in units of the lattice constant.86 The critical exponent of the correlation length is ν = 0.63002(10).63 The system is limited by two confining surfaces along the z coordinate (Fig. 1) and is periodic in the x and y directions. We have considered the so-called normal surface universality class,49,50,81 which corresponds to an infinitely strong surface field applied to the surface sites of the lattice (hα1 = ±∞, α ∈ {top,bot} for the upper or lower wall). This implies that effectively the surface spins are frozen (i.e., they do not fluctuate) and their values are set to +1 or −1, depending on the sign of hα1.The colloids are defined by drawing a sphere of radius R with its center located at a lattice site, and all spins within this sphere are treated as being frozen (ref. 64 and Section S2 in the ESI†). Similar to the slit walls, we consider colloids the surfaces of which belong to the normal surface universality class, and hence we also fixed the spins on the lattice sites neighboring the sites of the colloid surfaces.
The critical Casimir potential was calculated by computing the difference between the insertion free energies of the system with two colloids (placed along the x direction, see Fig. 1) separated by a distance D and a system with two colloids a distance Dmax apart, where Dmax is a sufficiently large separation at which two colloids de facto do not interact with each other (Section S2 in the ESI†). In most of our calculations the system size in terms of lattice sites was Nx × Ny = 100 × 40 large in the x and y directions; the size in the z direction is determined by the slit width. We used the hybrid MC method,87 in which each MC step consists of a combination of Wolff cluster update and Nx × Ny × Nz/2 single spin Metropolis updates. For thermalization, 1–2 × 105 MC steps were performed and thermal averaging was obtained from more than 1–2 × 106 hybrid MC steps, which have been split into 10 series for the evaluation of the statistical errors. In order to check the presence of hysteresis loops we proceeded in the same way as for the MFT analysis. In these simulations, which probe metastable states, we did not use the cluster moves in order to prevent the system from jumping into the global minimum.
Calculation of the colloidal phase diagram
We have considered the case that the colloids position themselves in the mid-plane of a slit, as shown schematically in Fig. 1. For thin slits this is a minor restriction (Fig. S6 in the ESI†). Accordingly, we studied a two-dimensional system of colloids with its grand canonical thermodynamic potential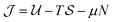 as the sum of the contributions due to the excluded volume and the long-ranged critical Casimir interactions; here μ is the chemical potential and N = ρA is the number of colloids (ρ is the two-dimensional density of colloids and A the surface area). Using the random phase approximation one readily obtains
as the sum of the contributions due to the excluded volume and the long-ranged critical Casimir interactions; here μ is the chemical potential and N = ρA is the number of colloids (ρ is the two-dimensional density of colloids and A the surface area). Using the random phase approximation one readily obtains 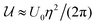 , where η = πρσ2 is the two-dimensional colloidal packing fraction,
, where η = πρσ2 is the two-dimensional colloidal packing fraction, 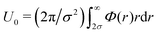 is an interaction parameter, and σ is the hard-disk radius. Considering charged colloids, we included the (short-ranged) screened electrostatic repulsion into the hard-disk reference system so that σ > R, where R is the geometric radius of the colloidal particles. We used Rowlinson's description88 of the hard sphere system in order to determine σ. For the entropy
is an interaction parameter, and σ is the hard-disk radius. Considering charged colloids, we included the (short-ranged) screened electrostatic repulsion into the hard-disk reference system so that σ > R, where R is the geometric radius of the colloidal particles. We used Rowlinson's description88 of the hard sphere system in order to determine σ. For the entropy 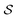 we used the analytical expression for hard discs following from scaled-particle theory.89,90 In order to obtain an equilibrium packing fraction for a given chemical potential, we minimized
we used the analytical expression for hard discs following from scaled-particle theory.89,90 In order to obtain an equilibrium packing fraction for a given chemical potential, we minimized 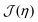 numerically. The colloidal phase diagram was constructed by identifying the region in which
numerically. The colloidal phase diagram was constructed by identifying the region in which 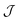 has two minima corresponding to high and low packing fractions. For details of the calculations see Section S3 in the ESI.†
has two minima corresponding to high and low packing fractions. For details of the calculations see Section S3 in the ESI.†
Conflicts of interest
There are no conflicts to declare.References
- V. N. Manoharan, Colloidal matter: packing, geometry, and entropy, Science, 2015, 349, 942 CrossRef CAS PubMed.
- E. Dickinson, Colloids in food: ingredients, structure, and stability, Annu. Rev. Food Sci. Technol., 2015, 6, 211–233 CrossRef CAS PubMed.
- ed. E. Matijevic, Medical Applications of Colloids, Springer, New York, 2008 Search PubMed.
- N. Geerts and E. Eiser, DNA-functionalized colloids: physical properties and applications, Soft Matter, 2010, 6, 4647–4660 RSC.
- ed. M. Fanun, Colloids in Biotechnology, Surfactant Science, CRC, Boca Raton, 2010 Search PubMed.
- ed. T. Ngai and S. Bon, Particle-Stabilized Emulsions and Colloids, RSC Soft Matter Series, The Royal Society of Chemistry, Cambridge, 2015, pp. 001–322 Search PubMed.
- S. Golde, T. Palberg and H. J. Schöpe, Correlation between dynamical heterogeneieties and structural heterogeneieties in colloidal hard sphere suspensions, Nat. Phys., 2016, 12, 712–717 CrossRef CAS.
- D. Beysens and D. Estève, Adsorption phenomena at the surface of silica spheres in a binary liquid mixture, Phys. Rev. Lett., 1985, 54, 2123–2126 CrossRef CAS PubMed.
- D. Beysens and T. Narayanan, Wetting-induced aggregation of colloids, J. Stat. Phys., 1999, 95, 997–1008 CrossRef.
- P. D. Gallagher, M. L. Kurnaz and J. V. Maher, Aggregation in polystyrene-sphere suspensions in near-critical binary liquid mixtures, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 46, 7750–7755 CrossRef.
- T. Narayanan, A. Kumar, E. S. R. Gopal, D. Beysens, P. Guenoun and G. Zalczer, Reversible flocculation of silica colloids in liquid mixtures, Phys. Rev. E, 1993, 48, 1989–1994 CrossRef CAS.
- J. G. Brankov, D. M. Danchev and N. S. Tonchev, Theory of critical phenomena in finite-size systems: scaling and quantum effects, Series in Modern Condensed Matter Physics, World Scientific, Singapore, 2000, vol. 9 Search PubMed.
- A. Gambassi, The Casimir effect: from quantum to critical fluctuations, J. Phys.: Conf. Ser., 2009, 161, 012037 CrossRef.
- D. Bonn, J. Otwinowski, S. Sacanna, H. Guo, G. Wegdam and P. Schall, Direct observation of colloidal aggregation by critical Casimir forces, Phys. Rev. Lett., 2009, 103, 156101 CrossRef PubMed; A. Gambassi and S. Dietrich, Colloidal aggregation and critical Casimir forces, Phys. Rev. Lett., 2010, 105, 059601 CrossRef PubMed; D. Bonn, G. Wegdam and P. Schall, Bonn, Wegdam, and Schall Reply, Phys. Rev. Lett., 2010, 105, 059602 CrossRef.
- S. J. Veen, O. Antoniuk, B. Weber, M. A. C. Potenza, S. Mazzoni, P. Schall and G. H. Wegdam, Colloidal aggregation in microgravity by critical Casimir forces, Phys. Rev. Lett., 2012, 109, 248302 CrossRef PubMed.
- H. Guo, T. Narayanan, M. Sztuchi, P. Schall and G. H. Wegdam, Reversible phase transition of colloids in a binary liquid solvent, Phys. Rev. Lett., 2008, 100, 188303 CrossRef PubMed.
- V. D. Nguyen, S. Faber, Z. Hu, G. H. Wegdam and P. Schall, Controlling colloidal phase transitions with critical Casimir forces, Nat. Commun., 2013, 4, 1584 CrossRef PubMed.
- M. T. Dang, A. V. Verde, V. D. Nguyen, P. G. Bolhuis and P. Schall, Temperature-sensitive colloidal phase behavior induced by critical Casimir forces, J. Chem. Phys., 2013, 139, 094903 CrossRef PubMed.
- T. F. Mohry, S. Kondrat, A. Macioek and S. Dietrich, Critical Casimir interactions around the consolute point of a binary solvent, Soft Matter, 2014, 10, 5510–5522 RSC.
- J. R. Edison, N. Tasios, S. Belli, R. Evans, R. van Roij and M. Dijkstra, Critical Casimir forces and colloidal phase transitions in a near-critical solvent: a simple model reveals a rich phase diagram, Phys. Rev. Lett., 2015, 114, 038301 CrossRef PubMed.
- N. Tasios, J. R. Edison, R. van Roij, R. Evans and M. Dijkstra, Critical Casimir interactions and colloidal self-assembly in near-critical solvents, J. Chem. Phys., 2016, 145, 084902 CrossRef PubMed.
- S. G. Stuij, M. Labbé-Laurent, T. E. Kodger, A. Maciołek and P. Schall, Critical casimir interactions between colloids around the critical point of binary solvents, Soft Matter, 2017, 13, 5233–5249 RSC.
- P. Pieranski, Colloidal crystals, Contemp. Phys., 1983, 24, 25–73 CrossRef CAS.
- A. Yethiraj and A. van Blaaderen, A colloidal model system with an interaction tunable from hard sphere to soft and dipolar, Nature, 2003, 421, 513–517 CrossRef CAS PubMed.
- G. L. Hunter and E. R. Weeks, The physics of the colloidal glass transition, Rep. Prog. Phys., 2012, 75, 066501 CrossRef PubMed.
- S. Singh, J. Houston, F. van Swol and C. J. Brinker, Superhydrophobicity: drying transition of confined water, Nature, 2006, 442, 526 CrossRef CAS PubMed.
- K. Koga, G. T. Gao, H. Tanaka and X. C. Zeng, Formation of ordered ice nanotubes inside carbon nanotubes, Nature, 2001, 412, 802–805 CrossRef CAS PubMed.
- S. Han, M. Y. Choi, P. Kumar and H. E. Stanley, Phase transitions in confined water nanofilms, Nat. Phys., 2010, 6, 685–689 CrossRef CAS.
- J. Chmiola, G. Yushin, Y. Gogotsi, C. Portet, P. Simon and P. L. Taberna, Anomalous increase in carbon capacitance at pore sizes less than 1 nanometer, Science, 2006, 313, 1760 CrossRef CAS PubMed.
- S. Kondrat and A. Kornyshev, Superionic state in double-layer capacitors with nanoporous electrodes, J. Phys.: Condens. Matter, 2011, 23, 022201 CrossRef CAS PubMed.
- M. Sadhukhan and A. Tkatchenko, Long-range repulsion between spatially confined van der Waals dimers, Phys. Rev. Lett., 2017, 118, 210402 CrossRef PubMed.
- A. Reinmüller, E. C. Oğuz, R. Messina, H. Löwen, H. J. Schöpe and T. Palberg, Confined colloidal crystals in and out of equilibrium, Eur. Phys. J.: Spec. Top., 2013, 222, 3011–3022 CrossRef.
- J. Bleibel, A. Domínguez and M. Oettel, Onset of anomalous diffusion in colloids confined to quasimonolayers, Phys. Rev. E, 2017, 95, 032604 CrossRef CAS PubMed.
- K. Nygard, Colloidal diffusion in confined geometries, Phys. Chem. Chem. Phys., 2017, 19, 23632–23641 RSC.
- G. Wu, H. Cho, D. A. Wood, A. D. Dinsmore and S. Yang, Confined assemblies of colloidal particles with soft repulsive interactions, J. Am. Chem. Soc., 2017, 139, 5095–5101 CrossRef CAS PubMed.
- Q.-H. Wei, C. Bechinger, D. Rudhardt and P. Leiderer, Experimental study of laser-induced melting in two-dimensional colloids, Phys. Rev. Lett., 1998, 81, 2606–2609 CrossRef CAS.
- H. Löwen, Twenty years of confined colloids: from confinement-induced freezing to giant breathing, J. Phys.: Condens. Matter, 2009, 21, 474203 CrossRef PubMed.
- C. A. Murray and D. H. V. Winkle, Experimental observation of two-stage melting in a classical two-dimensional screened Coulomb system, Phys. Rev. Lett., 1987, 58, 1200–1204 CrossRef CAS PubMed.
- E. Chang and D. W. Hone, Melting of a two-dimensional colloidal crystal confined between charged plates, EPL, 1988, 5, 635–639 CrossRef CAS.
- K. Zahn, R. Lenke and G. Maret, Two-stage melting of paramagnetic colloidal crystals in two dimensions, Phys. Rev. Lett., 1999, 82, 2721–2724 CrossRef CAS.
- K. Binder, S. Sengupta and P. Nielaba, The liquid–solid transition of hard discs: first-order transition or Kosterlitz–Thouless–Halperin–Nelson–Young scenario?, J. Phys.: Condens. Matter, 2002, 14, 2323 CrossRef CAS.
- S. van Teeffelen, C. N. Likos, N. Hoffmann and H. Löwen, Density functional theory of freezing for soft interactions in two dimensions, EPL, 2006, 75, 583 CrossRef CAS.
- U. Gasser, Crystallization in three- and two-dimensional colloidal suspensions, J. Phys.: Condens. Matter, 2009, 21, 203101 CrossRef CAS PubMed.
- Z. Cai, N. L. Smith, J.-T. Zhang and S. A. Asher, Two-dimensional photonic crystal chemical and biomolecular sensors, Anal. Chem., 2015, 87, 5013–5025 CrossRef CAS PubMed.
- M. E. Fisher and P. G. de Gennes, Phénomènes aux parois dans un mélange binaire critique, C. R. Seances Acad. Sci., Ser. B, 1978, 287, 207–209 CAS.
- C. Hertlein, L. Helden, A. Gambassi, S. Dietrich and C. Bechinger, Direct measurement of critical Casimir forces, Nature, 2008, 451, 172–175 CrossRef CAS PubMed.
- H. B. G. Casimir, On the attraction between two perfectly conducting plates, Proc., K. Acad. Sci. Amsterdam, 1948, 51, 793 Search PubMed , online available at the KNAW Digital Library.
- H. W. Diehl, The theory of boundary critical phenomena, Int. J. Mod. Phys. B, 1997, 11, 3503–3523 CrossRef.
- K. Binder, Critical behaviour at surfaces, in Phase Transitions and Critical Phenomena, ed. C. Domb and J. L. Lebowitz, Academic, London, 1983, vol. 8, p. 2 Search PubMed.
- H. W. Diehl, Field-theory of surface critical behaviour, in Phase Transitions and Critical Phenomena, ed. C. Domb and J. L. Lebowitz, Academic, London, 1986, vol. 10, p. 75 Search PubMed.
- T. G. Mattos, L. Harnau and S. Dietrich, Three-body critical Casimir forces, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 042304 CrossRef CAS PubMed.
- T. G. Mattos, L. Harnau and S. Dietrich, Many-body effects for critical Casimir forces, J. Chem. Phys., 2013, 138, 074704 CrossRef CAS PubMed.
- S. Kondrat, L. Harnau and S. Dietrich, Critical Casimir interaction of ellipsoidal colloids with a planar wall, J. Chem. Phys., 2009, 131, 204902 CrossRef CAS PubMed.
- S. Kondrat, F3DM library and tools, The F3DM library can be downloaded from http://sourceforge.net/projects/f3dm/.
- S. Paladugu, A. Callegari, Y. Tuna, L. Barth, S. Dietrich, A. Gambassi and G. Volpe, Nonadditivity of critical Casimir forces, Nat. Commun., 2016, 7, 11403 CrossRef CAS PubMed.
- C. Bauer, T. Bieker and S. Dietrich, Wetting-induced effective interaction potential between spherical particles, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 5324–5338 CrossRef CAS.
- A. J. Archer, R. Evans, R. Roth and M. Oettel, Solvent mediated interactions close to fluid–fluid phase separation: Microscopic treatment of bridging in a soft-core fluid, J. Chem. Phys., 2005, 122, 084513 CrossRef CAS PubMed.
- R. Okamoto and A. Onuki, Attractive interaction and bridging transition between neutral colloidal particles due to preferential adsorption in a near-critical binary mixture, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 022309 CrossRef PubMed.
- M. Labbe-Laurent, A. D. Law and S. Dietrich, Liquid bridging of cylindrical colloids in near-critical solvents, J. Chem. Phys., 2017, 147, 104701 CrossRef CAS PubMed.
- E. Koos, Capillary suspensions: particle networks formed through the capillary force, Curr. Opin. Colloid Interface Sci., 2014, 19, 575–584 CrossRef CAS PubMed.
- A. Hanke, F. Schlesener, E. Eisenriegler and S. Dietrich, Critical Casimir forces between spherical particles in fluids, Phys. Rev. Lett., 1998, 81, 1885–1888 CrossRef CAS.
- F. Schlesener, A. Hanke and S. Dietrich, Critical Casimir forces in colloidal suspensions, J. Stat. Phys., 2003, 110, 981–1013 CrossRef CAS.
- M. Hasenbusch, Finite size scaling study of lattice models in the three-dimensional Ising universality class, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 174433 CrossRef.
- O. A. Vasilyev, Critical Casimir interactions between spherical particles in the presence of bulk ordering fields, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 012138 CrossRef CAS PubMed.
- J. C. Crocker and D. G. Grier, Microscopic measurement of the pair interaction potential of charge-stabilized colloid, Phys. Rev. Lett., 1994, 73, 352 CrossRef CAS PubMed.
- G. M. Kepler and S. Fraden, Attractive potential between confined colloids at low ionic strength, Phys. Rev. Lett., 1994, 73, 356 CrossRef CAS PubMed.
- A. Reinmüller, E. C. Oğuz, R. Messina, H. Löwen, H. J. Schöpe and T. Palberg, Colloidal crystallization in the quasi-two-dimensional induced by electrolyte gradients, J. Chem. Phys., 2012, 136, 164505 CrossRef PubMed.
- M. Gross, O. Vasilyev, A. Gambassi and S. Dietrich, Critical adsorption and critical Casimir forces in the canonical ensemble, Phys. Rev. E, 2016, 94, 022103 CrossRef PubMed.
- A. Pelissetto and E. Vicari, Critical phenomena and renormalization-group theory, Phys. Rep., 2002, 368, 549–727 CrossRef CAS.
- P. Nowakowski and M. Napiórkowski, Lateral critical Casimir force in 2d Ising strip with inhomogeneous walls, J. Chem. Phys., 2014, 141, 064704 CrossRef PubMed.
- P. Nowakowski and M. Napiórkowski, Lateral critical Casimir force in two-dimensional inhomogeneous Ising strip. Exact results, J. Chem. Phys., 2016, 144, 214703 CrossRef PubMed.
- A. Malijevský, Effective interactions between a pair of nanoparticles, Mol. Phys., 2015, 113, 1170–1178 CrossRef.
- A. Malijevský and A. O. Parry, Bridging transitions for spheres and cylinders, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 022407 CrossRef PubMed.
- C. Gögelein, M. Brinkmann, M. Schröter and S. Herminghaus, Controlling the formation of capillary bridges in binary liquid mixtures, Langmuir, 2010, 26, 17184–17189 CrossRef PubMed.
- A. O. Parry and R. Evans, Influence of wetting on phase equilibria: a novel mechanism for critical-point shifts in films, Phys. Rev. Lett., 1990, 64, 439–442 CrossRef CAS PubMed.
- A. O. Parry and R. Evans, Novel phase behaviour of a confined fluid or Ising magnet, Physica A, 1992, 181, 250–296 CrossRef CAS.
- K. Binder, D. P. Landau and A. M. Ferrenberg, Character of the phase transition in thin Ising films with competing walls, Phys. Rev. Lett., 1995, 74, 298–301 CrossRef CAS PubMed.
- K. Binder, D. P. Landau and A. M. Ferrenberg, Thin Ising films with competing walls: a Monte Carlo study, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 2823–2838 CrossRef CAS.
- K. Binder, D. Landau and M. Müller, Monte Carlo studies of wetting, interface localization and capillary condensation, J. Stat. Phys., 2003, 110, 1411–1514 CrossRef.
- B. J. Schulz, K. Binder and M. Müller, First-order interface localization–delocalization transition in thin Ising films using Wang–Landau sampling, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 046705 CrossRef CAS PubMed.
- T. F. Mohry, A. Maciołek and S. Dietrich, Crossover of critical Casimir forces between different surface universality classes, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 061117 CrossRef CAS PubMed.
- S. Kondrat, L. Harnau and S. Dietrich, Critical adsorption on nonspherical colloidal particles, J. Chem. Phys., 2007, 126, 174902 CrossRef CAS PubMed.
- M. Tröndle, S. Kondrat, A. Gambassi, L. Harnau and S. Dietrich, Normal and lateral critical Casimir forces between colloids and patterned substrates, EPL, 2009, 88, 40004 CrossRef.
- M. Tröndle, S. Kondrat, A. Gambassi, L. Harnau and S. Dietrich, Critical Casimir effect for colloids close to chemically patterned substrates, J. Chem. Phys., 2010, 133, 074702 CrossRef PubMed.
- T. F. Mohry, A. Maciołek and S. Dietrich, Phase behavior of colloidal suspensions with critical solvents in terms of effective interactions, J. Chem. Phys., 2012, 136, 224902 CrossRef CAS PubMed.
- C. Ruge, P. Zhu and F. Wagner, Correlation function in Ising models, Physica A, 1994, 209, 431 CrossRef.
- D. P. Landau and K. Binder, A Guide to Monte Carlo Simulations in Statistical Physics, Cambridge University, London, 2005 Search PubMed.
- J. Rowlinson, The statistical mechanics of systems with steep intermolecular potentials, Mol. Phys., 1964, 8, 107–115 CrossRef CAS.
- H. Reiss, H. L. Frisch and J. L. Lebowitz, Statistical mechanics of rigid spheres, J. Chem. Phys., 1959, 31, 369–380 CrossRef CAS.
- E. Helfand, H. L. Frisch and J. L. Lebowitz, Theory of the two- and one-dimensional rigid sphere fluids, J. Chem. Phys., 1961, 34, 1037 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7sm01363a |
| This journal is © The Royal Society of Chemistry 2018 |