Open Access Article
Open Access ArticleDisentanglement of excited-state dynamics with implications for FRET measurements: two-dimensional electronic spectroscopy of a BODIPY-functionalized cavitand†
John P.
Otto‡
a,
Lili
Wang‡
 a,
Igor
Pochorovski
b,
Samuel M.
Blau
c,
Alán
Aspuru-Guzik
a,
Igor
Pochorovski
b,
Samuel M.
Blau
c,
Alán
Aspuru-Guzik
 cd,
Zhenan
Bao
*b,
Gregory S.
Engel
cd,
Zhenan
Bao
*b,
Gregory S.
Engel
 *a and
Melanie
Chiu§
*a and
Melanie
Chiu§
 *b
*b
aDepartment of Chemistry, University of Chicago, Chicago, IL 60637, USA. E-mail: gsengel@uchicago.edu
bDepartment of Chemical Engineering, Stanford University, Stanford, CA 94305, USA. E-mail: zbao@stanford.edu; melanie.chiu@stonybrook.edu
cDepartment of Chemistry and Chemical Biology, Harvard University, Cambridge, MA 02138, USA
dSenior Fellow, Canadian Institute for Advanced Research, Toronto, Ontario M5G 1Z8, Canada
First published on 15th March 2018
Abstract
Förster Resonance Energy Transfer (FRET) is the incoherent transfer of an electronic excitation from a donor fluorophore to a nearby acceptor. FRET has been applied as a probe of local chromophore environments and distances on the nanoscale by extrapolating transfer efficiencies from standard experimental parameters, such as fluorescence intensities or lifetimes. Competition from nonradiative relaxation processes is often assumed to be constant in these extrapolations, but in actuality, this competition depends on the donor and acceptor environments and can, therefore, be affected by conformational changes. To study the effects of nonradiative relaxation on FRET dynamics, we perform two-dimensional electronic spectroscopy (2DES) on a pair of azaboraindacene (BODIPY) dyes, attached to opposite arms of a resorcin[4]arene cavitand. Temperature-induced switching between two equilibrium conformations, vase at 294 K to kite at 193 K, increases the donor–acceptor distance from 0.5 nm to 3 nm, affecting both FRET efficiency and nonradiative relaxation. By disentangling different dynamics based on lifetimes extracted from a series of 2D spectra, we independently observe nonradiative relaxation, FRET, and residual fluorescence from the donor in both vase to kite conformations. We observe changes in both FRET rate and nonradiative relaxation when the molecule switches from vase to kite, and measure a significantly greater difference in transfer efficiency between conformations than would be determined by standard lifetime-based measurements. These observations show that changes in competing nonradiative processes must be taken into account when highly accurate measurements of FRET efficiency are desired.
Introduction
Förster Resonance Energy Transfer (FRET) moves an excitation nonradiatively from a donor fluorophore to a nearby acceptor via dipole–dipole interactions.1 FRET can be elegantly described by readily accessible experimental parameters, such as the distance between chromophores (R), the fluorescence spectrum of the donor, and the absorption spectrum of the acceptor.2 The mechanism's well known R−6 distance dependence has led to widespread application3,4 of FRET as a spectroscopic measure of distances on the single nanometer scale.5,6 In particular, FRET is often used to probe interactions between biomolecules such as proteins6–10 and DNA11–14 and to image those interactions within cells.15–21 An extensive array of donor–acceptor pairs has been developed for these purposes.8,12,22–28In Förster's model, the coupling between the donor and acceptor electronic states is treated as a second-order perturbation in the electronic coupling. The interaction is governed by the transition dipole moments of the excited electronic states. The coupling is sufficiently weak (and the transfer rate therefore sufficiently slow) that the donor relaxes to thermal vibrational equilibrium in its electronic excited state before transfer can occur. Although no absorption or emission occurs in the transfer itself (FRET is nonradiative), the same transition dipoles that are responsible for donor emission and acceptor absorption also drive the transfer, so resonance can be determined by absorption and emission spectra, and transfer competes with donor fluorescence and nonradiative relaxation.
Experimentally, FRET efficiency can be determined by photon counts of donor or acceptor fluorescence or by changes in the donor's decay lifetime.17,29 The latter approach is often preferred due to relative immunity to cross-talk and concentration artifacts,7,16,22 and is based on kinetic competition of decay processes. In this scenario, efficiency can be expressed as
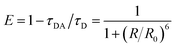 | (1) |
| 1/τD = kD = kD,f + kD,nr | (2a) |
| 1/τDA = kDA = kD,f + kD,nr + ktr | (2b) |
To investigate the interactions between nonradiative relaxation and FRET, we sought a pair of chromophores that undergo both excited-state processes. Moreover, we sought a means of exerting control over both the distance separating the chromophore pair and the vibrational bath that defines the local environment of each chromophore. Quinoxaline-bridged resorcin[4]arene cavitands emerged as ideal molecular scaffolds for fulfilling the latter requirement, as these conformational switches can be toggled between a pursed vase state and a ringent, kite state using various external stimuli, including temperature.31,32 Due to solvation-related entropic effects, the cavitand exists in the vase conformation at room temperature and above; conformational switching commences at ca. 223 K, and at 193 K, only the kite conformation is observed.33 To adapt this scaffold for our studies, we sought to append each of a pair of chromophores to opposing walls of the cavitand.34–36 We selected a pair of arylethynyl-functionalized azaboraindacene (BODIPY) chromophores for this purpose because they exhibit the requisite photophysical properties,37–39 and because both a donor and an acceptor chromophore are conveniently accessible from a single, divergent synthetic route.40
Given the ability of 2DES measurements to elucidate ultrafast transfer and relaxation dynamics in both biological41–43 and synthetic systems,44–46 we sought to study the BODIPY-functionalized cavitand using this technique. By separating the signal based on time dynamics, we disentangle three relaxation pathways (nonradiative relaxation, energy transfer, and residual fluorescence) and isolate their lineshapes from the donor in both conformations (kite at 193 K and vase at 294 K). Based on our signal isolation analysis, we observe that the contribution of nonradiative relaxation to the overall donor decay changes with conformation. We show that, due to this change in nonradiative relaxation, fluorescence lifetime measurements underreport the transfer efficiency difference between kite and vase conformations, highlighting the need to test assumptions about nonradiative processes when measuring FRET in complex environments.
Results and discussion
Synthesis, variable-temperature characterization, and computed structures of the BODIPY-functionalized resorcin[4]arene cavitand
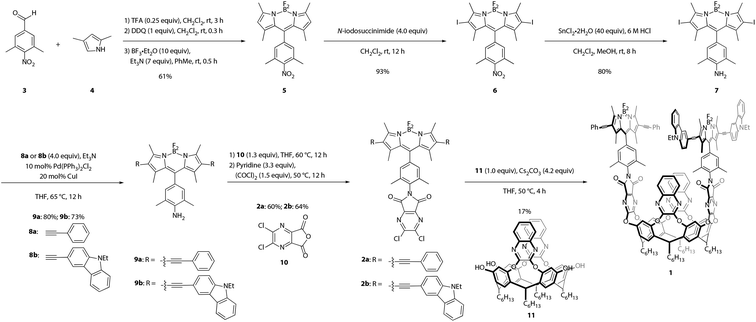
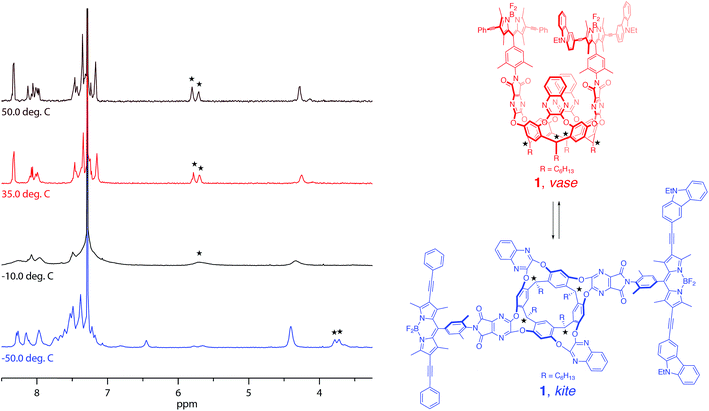
Synthesis of the target cavitand 1, a new compound, was based on various precedents in the BODIPY and resorcin[4]arene literatures as indicated below. The process commenced with preparation of BODIPY-functionalized walls 2a and 2b (Scheme 1). Condensation of commercially available nitrobenzaldehyde 3 with 2,4-dimethylpyrrole (4) provided the nitro-BODIPY core 5.47 Treatment of nitro-BODIPY 5 with 4 equiv. N-iodosuccinimide yielded diiodo-BODIPY 6, which was subsequently converted to anilino-BODIPY 7 using stannous chloride to selectively reduce the nitro moiety without affecting the iodides.48 Sonogashira cross-coupling of anilino-BODIPY 7 with phenylacetylene (8a) yielded donor dye 9a; acceptor dye 9b was prepared analogously using N-ethylcarbazoyl alkyne 8b.40 Condensation of donor dye 9a and acceptor dye 9b with anhydride 10 afforded walls 2a and 2b, respectively.34 Final assembly of cavitand 1, which involves four nucleophilic substitutions, was achieved in a one-pot procedure with 17% yield, wherein a mixture of tetrol 11 and both walls, 2a and 2b, were treated with cesium carbonate. Target cavitand 1 was purified from the resultant mixture using flash column chromatography, followed by recycling gel permeation chromatography. The successful installation of two different walls on tetrol 11 in one pot to access cavitand 1 represents an alternative to previously reported methods for synthesizing non-symmetrically-substituted resorcin[4]arene cavitands. The one-pot reaction obviates the need for multiple purification steps which reduce overall yield.34Temperature-dependent conformational behavior of cavitand 1 was characterized by variable-temperature 1H NMR,33 absorption, and fluorescence spectroscopies.34 As shown in Fig. 1, the 1H NMR spectrum of cavitand 1 at 323 K exhibits two sets of sharp multiplets between 5.7 and 5.8 ppm, corresponding to the resorcin[4]arene methine protons (★) and indicative of the vase conformation. Cooling the sample to 223 K resulted in a diagnostic upfield shift of these methine proton signals to ca. 3.8 ppm due to increased shielding from the proximity of the aromatic wall flaps in the kite conformation. Consistent with previous reports, the vase-to-kite transition was also observed upon addition of acid (see Fig. S27 in the ESI†).34
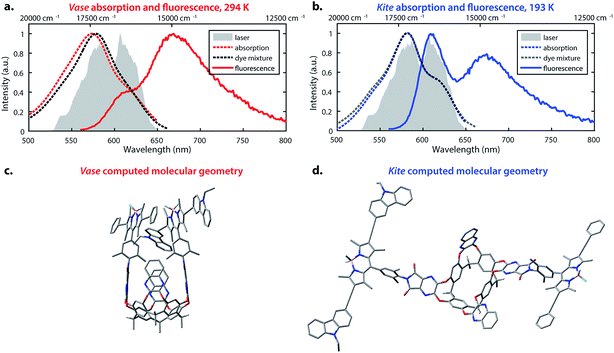
The temperature-dependent conformational switching of cavitand 1 was corroborated by fluorescence and absorption spectroscopies, as depicted in Fig. 2. The vase conformation of cavitand 1 predominates at 294 K (Fig. 2a), evidenced by a blue-shift of the absorption maximum of cavitand 1 relative to that of the dye mixture; interactions between the donor and acceptor dyes in the vase conformation of cavitand 1 result in shifts of their ground- and excited-state energies. At 193 K, the absorption spectrum of cavitand 1 resembles that of the dye mixture, which is consistent with the weak interaction between the donor and acceptor dyes in the kite conformation (Fig. 2b). Fluorescence spectra of cavitand 1 at 294 K and 193 K (excitation at 525 nm for both conformations) show a clear increase in donor emission at 610 nm with a concurrent decrease in acceptor emission at 670 nm as the temperature is lowered. These fluorescence changes indicate a decrease in FRET efficiency and an increase in the distance between the donor and acceptor dye at lower temperature, which is consistent with conversion of vase to kite with decreasing temperature.
Computational studies provided further structural insights into the two conformations of cavitand 1. The geometries of the vase and kite conformations were optimized using density functional theory calculations (B3LYP/3-21G(d)) in the Gaussian 09 software package,49 and are depicted in Fig. 2c and d, respectively. In both conformations, terminal C6H13 groups on the cavitand base have been replaced with CH3. In the vase conformation, the donor and acceptor are sterically constrained to an orientation that promotes dipole–dipole coupling. The donor–acceptor distance in the vase conformation is ca. 0.5 nm, which is too close for independent solvation of the two chromophores, suggesting that they interact vibrationally, as well as electronically. In contrast, the donor and acceptor are separated by ca. 3 nm in the kite conformation, providing the chromophores with relative orientational freedom. Although the donor and acceptor are separated by less than R0, they interact weakly enough that the approximations made by FRET theory accurately describe their interaction. Having successfully synthesized cavitand 1 and confirmed that its conformation and transfer dynamics could be externally controlled by temperature, we next sought to probe the excited-state dynamics of cavitand 1, focusing on the interactions between nonradiative relaxation and FRET processes.
Two-dimensional electronic spectroscopy
Two-dimensional electronic spectroscopy (2DES) is a four-wave mixing technique that uses three ultrafast pulses at controlled time delays to interact with a sample, generating a third-order nonlinear signal. Two frequency axes, ωτ and ωt, are produced via Fourier transformation over the first and third time delays (coherence time, τ, and rephasing time, t). These axes represent the frequencies of excitation and detection, respectively, and correspond to the horizontal (ωτ) and vertical (ωt) axes on all 2D spectra shown in this paper. Plotted as the change in transmitted light (ΔT), positive features can be attributed to stimulated emission (SE) or to ground state bleach (GSB; a decrease in absorption caused by depletion of the ground state population). Negative features are due to excited state absorption (ESA). Signal recorded at a series of waiting times (T) can reveal the time dynamics of the interrogated sample over 5–6 orders of magnitude, ranging from femtoseconds to nanoseconds.2D spectra are frequency–frequency correlation maps, describing the optical response of a system (recorded on ωt axis) at a series of waiting times, T, after initial excitation at ωτ. Signals along the diagonal indicate features detected at the same energy as their excitation, while signals above or below the diagonal indicate coupling or population transfer between excited states. Additionally, the lineshapes of 2D signals provide information on the mechanisms that lead to broad spectral signals.50 Inhomogeneous broadening (extension along the diagonal) gives insight into static variation in chemical environments, which perturb the excitation energies of individual chromophores.51 In contrast, homogeneous broadening (which determines antidiagonal linewidth) occurs when frequency fluctuations due to bath interactions occur quickly compared with the experimental timescale, such that an individual chromophore experiences all configurations of its local environment during a given measurement and thus represents the entire ensemble.52 In the homogeneous limit, one can estimate the dephasing time of a transition (the time required to lose phase correlation in the ensemble of sample molecules) by its homogeneous linewidth.53
Two-dimensional electronic spectra of the BODIPY-functionalized cavitand
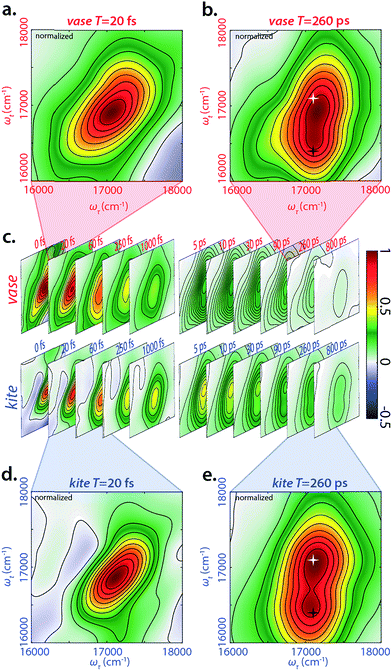
We performed 2DES measurements on the BODIPY-cavitand dimer at both 193 K and 294 K in two sets of waiting times—one from −20 to 1000 fs with a 10 fs step size, and the other from −5 to 800 ps with a 5 ps step size. Representative, real-valued 2D spectra for the kite and vase conformations of the dimer are shown in Fig. 3. Four logarithmically-spaced time series and highlighted time points are illustrated for comparison. The 2D spectra of each conformation in Fig. 3c are normalized to the maximum of 2D spectrum at T = 0 fs in both datasets, and the frames in the highlighted spectra (Fig. 3a, b, d, and e) are normalized individually.At T = 20 fs, 2D spectra of both vase (Fig. 3a) and kite (Fig. 3d) show an inhomogeneously broadened peak along the diagonal at roughly 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 cm−1. This signal corresponds to the initial absorption of the donor; at 20 fs the system has not yet relaxed past this starting point. Vibrational relaxation (aka Stokes shift) from this initial absorption occurs within the first 100 fs, leading to the below-diagonal cross peak in all subsequent spectra (see ESI† for more detail).
100 cm−1. This signal corresponds to the initial absorption of the donor; at 20 fs the system has not yet relaxed past this starting point. Vibrational relaxation (aka Stokes shift) from this initial absorption occurs within the first 100 fs, leading to the below-diagonal cross peak in all subsequent spectra (see ESI† for more detail).
At T = 260 ps (Fig. 3b and e), two dominant features are present in both 2D spectra—a diagonal peak at 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 cm−1 (white star) and a crosspeak at 17
100 cm−1 (white star) and a crosspeak at 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 cm−1 (585 nm) in ωτ and 16
100 cm−1 (585 nm) in ωτ and 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 (610 nm) cm−1 in ωt (black star). The diagonal feature at T = 260 ps is due to ground state bleach on the donor, because Stokes shift from the initial excitation has completed by this time. The below-diagonal crosspeak corresponds primarily to stimulated emission from the Stokes-shifted excited state of the donor. Along the anti-diagonal direction, all features are very broad, indicating the homogeneity of excited donor molecules. The width of these homogeneously broadened features is caused by rapid dephasing on the scale of tens of fs (Fig. S30†). A red shift in early time dynamics of the complex occurs on the same timescale, (see Fig. S31†) and the processes driving the red shift may also be the cause of this rapid dephasing. Further discussion of dephasing lifetimes and ultrafast dynamics can be found in the ESI.†
400 (610 nm) cm−1 in ωt (black star). The diagonal feature at T = 260 ps is due to ground state bleach on the donor, because Stokes shift from the initial excitation has completed by this time. The below-diagonal crosspeak corresponds primarily to stimulated emission from the Stokes-shifted excited state of the donor. Along the anti-diagonal direction, all features are very broad, indicating the homogeneity of excited donor molecules. The width of these homogeneously broadened features is caused by rapid dephasing on the scale of tens of fs (Fig. S30†). A red shift in early time dynamics of the complex occurs on the same timescale, (see Fig. S31†) and the processes driving the red shift may also be the cause of this rapid dephasing. Further discussion of dephasing lifetimes and ultrafast dynamics can be found in the ESI.†
Decay-associated spectra
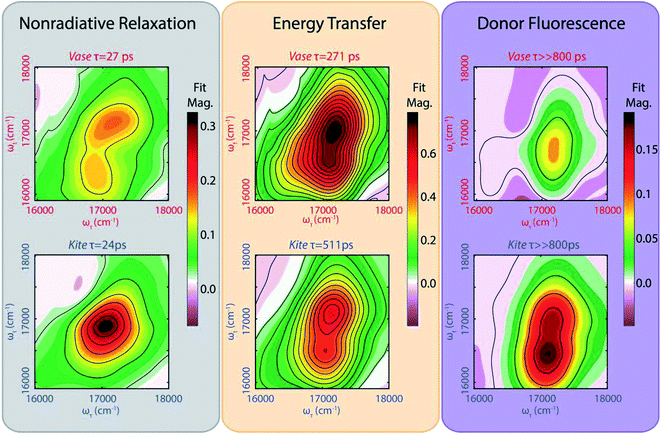
Decay-associated spectra (DAS) are generated from global fitting of the decay dynamics of each pixel in a 2D spectrum, and quantifying the contributions of various pathways to the overall signal. This and similar approaches have previously been applied to 2D spectra by the Engel group54 and others.55–58 We performed DAS analysis on the long waiting time (5 ps resolved) 2D data, specifically from 5 ps to 800 ps.The waiting time decay dynamics were fit to the following equation
| S(T) = A1e−T/τ1 + A2e−T/τ2 + A3 | (3) |
The left (grey) column in Fig. 4 shows a fast (∼25 ps) decay for cavitand 1 in the vase (294 K, top) and kite (193 K, bottom) conformations. These lifetimes are consistent with reports of a decay in the 15–30 ps range for analogous meso-aryl substituted boron dipyrrin structures.37,38 We assign this fast decay to a nonradiative, vibrationally driven relaxation arising from a combination of flexing in the dipyrrin backbone and rotation of the aryl group, as suggested by Li et al.38 and Kee et al.37 The multi-exponential nature of the decay means that this process (corresponding to the fastest exponential decay) does not compete kinetically with the processes observed in the other two exponential decays. This observation may be explained by a multi-well potential energy surface for the excited donor, as illustrated in Fig. 4 and observed by Li et. al.38
While the lifetimes of this nonradiative relaxation pathway are very similar for both conformations, the corresponding lineshapes in the 2D lifetime map differ notably. In the kite spectrum (Fig. 4, lower left plot, grey), the signal is primarily due to one homogeneously broadened feature at 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. The antidiagonal full width at half maximum (FWHM) of this feature corresponds to a homogeneous process with a dephasing lifetime of 48 fs, coincident with the timescale of relaxation within the electronic excited state as seen via Stokes shift in fs-resolved 2DES (Fig. S31†). By comparison, the vase spectrum (Fig. 3, upper left plot) shows an inhomogeneously broadened diagonal feature at 17
000 cm−1. The antidiagonal full width at half maximum (FWHM) of this feature corresponds to a homogeneous process with a dephasing lifetime of 48 fs, coincident with the timescale of relaxation within the electronic excited state as seen via Stokes shift in fs-resolved 2DES (Fig. S31†). By comparison, the vase spectrum (Fig. 3, upper left plot) shows an inhomogeneously broadened diagonal feature at 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 cm−1, as well as a crosspeak feature at an excitation frequency of 17
100 cm−1, as well as a crosspeak feature at an excitation frequency of 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 and detection frequency of 16
000 cm−1 and detection frequency of 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 cm−1. Inhomogeneous broadening indicates that subsections of the sample population have differing energetic environments, such as those arising from conformational variation, that persist on the timescale of the experiment.
400 cm−1. Inhomogeneous broadening indicates that subsections of the sample population have differing energetic environments, such as those arising from conformational variation, that persist on the timescale of the experiment.
The middle (orange) column in Fig. 4 represents the strength of signal that decays with a lifetime of several hundred ps. This decay lifetime is not observed in fluorescence lifetime measurements of the donor solution. We assign this signal to energy transfer between donor and acceptor (FRET). The energy of the diagonal feature matches with GSB from the donor, while the energy of the below-diagonal feature matches SE from the Stokes-shifted excited donor, as well as the absorption of the acceptor. Both features decay due to FRET transfer to the acceptor. Because the initial vibrational relaxation in the donor excited state is complete within 100 fs (Fig. S31†), all signal at the diagonal observed on this timescale is due to GSB of the donor, meaning that only the loss of donor excitation is observed. The below-diagonal features may contain signal from the acceptor and have longer lifetimes than features on the diagonal (Table TS4 in ESI†). Hence, the diagonal feature is used for donor lifetime measurements. This FRET transfer pathway contributes to the majority of the signal, particularly in the vase conformation where the chromophores are in close proximity to one another.
The right (purple) column in Fig. 4 shows the portion of the 2D signal that does not decay on the timescale of 800 ps. We assign this signal to residual donor fluorescence based on the measured fluorescence lifetime of the donor (2–3 ns, ESI Table TS2†). The double peak lineshape of this signal can be described by a combination of GSB at the diagonal (corresponding to the original absorption) and SE at the crosspeak (corresponding to Stokes-shifted emission). Simulated spectra generated from the absorption and fluorescence of the donor alone (Fig. S32†) qualitatively match the lineshape of this long-lived signal for both conformations, further supporting our assignment. Previous work on FRET between orthogonal dyes has highlighted that low frequency vibrations (analogous here to the difference in orientational freedom between vase and kite) can alter transfer efficiency dramatically.59
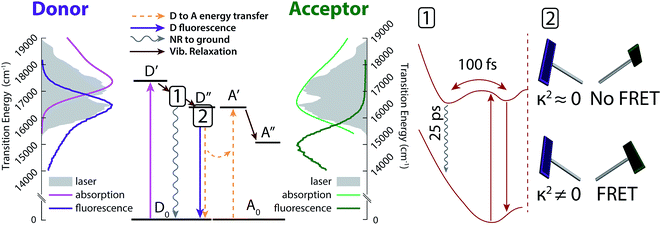
Conformation-dependent changes in excited-state dynamics and effects on FRET
The excited-state dynamic processes in cavitand 1 elucidated by 2DES and DAS analyses are summarized in Fig. 5. After absorption in the donor from ground state D0 to initial excited state D′, rapid vibrational relaxation on the excited state surface occurs within the first 100 fs, as shown in inset 1 of Fig. 5 (brown arrows). Excitations relax into (at least) two local minima, with one containing 20–30% of the original excited state population leading to nonradiative relaxation on a ∼25 ps timescale. All remaining excitations relax into the local minimum corresponding to dipole-driven relaxation, either as FRET or fluorescence. At this juncture, the available population of FRET donors is limited again, but by a distribution of dipole orientations between donor and acceptor. Inset 2 of Fig. 5 shows two example chromophore orientations in the kite conformation, one in which FRET occurs readily (bottom) and one in which FRET is prohibited as dipole coupling approaches zero (top). This distribution of dipole orientations leads to the two remaining decays illustrated in Fig. 5, one due to energy transfer (orange in Fig. 4, dashed orange arrows in Fig. 5), and one due to residual fluorescence (purple in Fig. 4, dark purple arrow in Fig. 5). With a rate of a few hundred ps, FRET is the dominant dipole-driven relaxation pathway for the donor, regardless of conformation. The acceptor then quickly relaxes out of our laser bandwidth and is not observed. While FRET remains the dominant pathway, conformational change between vase and kite affects both the transfer rate and the relative fractions of excited donor molecules decaying along all three paths.While we identify the second of the three lifetimes as corresponding to energy transfer, it should be noted that the measured lifetime is distinct from the time actually required for transfer. FRET relies upon the same dipole coupling between ground and excited states that leads to donor fluorescence, meaning that fluorescence always occurs along with FRET and that the branching ratio between them is determined by their relative rates. As such, the measured decay in excited state population will have a rate k2D such that
| k2D = ktr + kd,0 | (4) |
In addition to determining transfer lifetimes, we can calculate the branching ratio of FRET in this system using eqn (1), where τDA is the lifetime we assign to energy transfer in DAS and τD is the fluorescence decay lifetime of the donor in solution, measured via time-correlated single photon counting (TCSPC). This method results in a calculated transfer efficiency of 92.1 ± 1.3% transfer for the vase conformation and 78.0 ± 2.9% for the kite conformation. This approach only accounts for kinetic competition, however, and therefore only determines the efficiency of the subpopulation measured in DAS. If we use the peak diagonal intensities from DAS to approximate branching between the three subpopulations, we obtain overall FRET efficiencies of 68.7 ± 1.1% for the vase conformation and 44.3 ± 1.8% for the kite conformation, a significant reduction in overall values and a dramatically greater difference between conformations than the difference measured viaeqn (1).
The results above highlight how conformation-dependent variations in nonradiative relaxation processes affect the accuracy of lifetime-based FRET measurements. These effects should be considered in situations where the chromophore structure(s) or their relative orientations result in either: (1) breakdown of the ideal dipole approximation (IDA); or (2) appreciable competition in the excited state population between FRET and nonradiative relaxation. The former is relevant to chromophore structures that exhibit delocalized transition densities60,61 or to systems in which chromophore orientations are restricted such that isotropic dipole distributions that might mitigate IDA breakdown cannot be achieved.62,63 The latter situation might arise in donor chromophore structures that exhibit either modest quantum yields or conformational freedom that exacerbates nonradiative relaxation processes.37 In addition to considering the effect of variations in nonradiative relaxation on FRET measurements, these variations might also be exploited productively as probes for changing viscosity in cell environments via motion-induced change in emission measurements (MICE).64
Conclusion
When excited-state populations undergo competing FRET and nonradiative relaxation processes that change with donor–acceptor distance, the nonradiative relaxation processes must be accounted for in order to obtain accurate FRET efficiencies. To illustrate how nonradiative processes can affect FRET efficiency determinations, we designed a BODIPY-functionalized resorcin[4]arene cavitand that undergoes well-defined, temperature-induced conformational changes, allowing external control over donor–acceptor distance, as well as interactions between the chromophores and vibrational bath. The vase and kite conformations of the cavitand were subjected to 2DES studies, in which transitions could be separated with respect to both frequency and time, thereby enabling direct observation of changes in nonradiative relaxation that occur upon switching the cavitand conformation. Accurate determination of FRET efficiency required disambiguating overlapping transitions arising from nonradiative relaxation, FRET, and residual donor fluorescence; efficiencies extrapolated using this method differ significantly from those determined from lifetime measurements that assume that nonradiative relaxation is independent of conformation. Thus, in systems where nonradiative pathways compete with FRET, understanding how these pathways change with variations in donor and acceptor environments is vital for accurate determination of transfer efficiency. This understanding will enable improved FRET efficiency measurements in the complex environments inherent to biological systems and advanced materials.Experimental section
General methods
Detailed synthesis procedures and spectra are provided in the ESI.†UV/vis absorption spectra were recorded using a Cary 5000 dual-beam UV/VIS/NIR spectrophotometer. Steady state fluorescence was measured via a Horiba Fluorolog 3, and fluorescence quantum yields were recorded using the Horiba Quanta-Phi attachment. Time-domain lifetimes were measured on a ChronosBH lifetime fluorometer (ISS, Inc.) using Time-Correlated Single Photon Counting (TCSPC) methods. The fluorometer contained Becker-Hickl SPC-130 detection electronics and an HPM-100-40 Hybrid PMT detector. Tunable picosecond pulsed excitation at 560 nm was provided by a Fianium SC400-2 supercontinuum laser source with integrated pulse picker and AOTF. Emission wavelengths were selected with bandpass filters (Chroma HQ615/85 nm). The Instrument Response Function (IRF) was measured to be approximately 120 ps FWHM in a 1% scattering solution of Ludox LS colloidal silica. Multi-component exponential decay lifetimes were fit via a forward convolution method in the Vinci control and analysis software.
Two-dimensional electronic spectra were acquired using a homebuilt instrument that has been described previously.45 A Ti:sapphire oscillator and regenerative amplifier (Micra and Legend Elite, Coherent) generate a 5 kHz, 100 fs pulse train that is directed into a noncollinear optical parametric amplifier (NOPA, TOPAS). The output of the NOPA is then compressed using a prism pair followed by a spatial light modulator array (FemtoJock, Biophotonics). The resulting pulse (12 fs, 530–650 nm FWHM) is then split into four via a beamsplitter and a transmissive grating. The four beams are directed to the sample with a boxcar geometry. The time delays are controlled by paired glass wedges (coherence time, τ) and a translational stage (waiting time, T). Beams 1, 2 and 3 interact with the sample to generate the third-order signal. Beam 4 is attenuated by three orders of magnitude and serves as local oscillator for heterodyne detection. Signal, along with the local oscillator, is directed to a spectrometer and the resulting interferogram is recorded on a CCD array (Andor). All 2D data in the main text were collected in the same 24 h period in the same cryostat, varying only the temperature between the two measurements.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank the DARPA QuBE program (N66001-10-1-4060) and MRSEC (DMR 14-20709). The authors thank Dr Karen Watters for scientific editing of the manuscript.References
- T. Förster, in Istanbul Lectures, Part III: Action of Light and Organic Crystals, Academic Press, New York, 1965, pp. 93–137 Search PubMed.
- R. M. Clegg, Curr. Opin. Biotechnol., 1995, 6, 103–110 CrossRef CAS PubMed.
- P. R. Selvin, Nat. Struct. Biol., 2000, 7, 730–734 CrossRef CAS PubMed.
- P. G. Wu and L. Brand, Anal. Biochem., 1994, 218, 1–13 CrossRef CAS PubMed.
- L. Stryer and R. P. Haugland, Proc. Natl. Acad. Sci. U. S. A., 1967, 58, 719–726 CrossRef CAS.
- C. G. dos Remedios and P. D. Moens, J. Struct. Biol., 1995, 115, 175–185 CrossRef CAS PubMed.
- R. N. Day, A. Periasamy and F. Schaufele, Methods, 2001, 25, 4–18 CrossRef CAS PubMed.
- B. N. G. Giepmans, S. R. Adams, M. H. Ellisman and R. Y. Tsien, Science, 2006, 312, 217–224 CrossRef CAS PubMed.
- M. Tramier, I. Gautier, T. Piolot, S. Ravalet, K. Kemnitz, J. Coppey, C. Durieux, V. Mignotte and M. Coppey-Moisan, Biophys. J., 2002, 83, 3570–3577 CrossRef CAS PubMed.
- S. S. Vogel, C. Thaler and S. V. Koushik, Sci. STKE, 2006 DOI:10.1126/stke.3312006re2.
- V. V. Didenko, BioTechniques, 2001, 31, 1106–1121 CAS.
- A. Hillisch, M. Lorenz and S. Diekmann, Curr. Opin. Struct. Biol., 2001, 11, 201–207 CrossRef CAS PubMed.
- C.-Y. Zhang, H.-C. Yeh, M. T. Kuroki and T.-H. Wang, Nat. Mater., 2005, 4, 826–831 CrossRef CAS PubMed.
- S. Zadran, S. Standley, K. Wong, E. Otiniano, A. Amighi and M. Baudry, Appl. Microbiol. Biotechnol., 2012, 96, 895–902 CrossRef CAS PubMed.
- P. Bastiaens, Trends Cell Biol., 1999, 9, 48–52 CrossRef CAS PubMed.
- W. Becker, J. Microsc., 2012, 247, 119–136 CrossRef CAS PubMed.
- E. A. Jares-Erijman and T. M. Jovin, Nat. Biotechnol., 2003, 21, 1387–1395 CrossRef CAS PubMed.
- E. A. Jares-Erijman and T. M. Jovin, Curr. Opin. Chem. Biol., 2006, 10, 409–416 CrossRef CAS PubMed.
- R. B. Sekar and A. Periasamy, J. Cell Biol., 2003, 160, 629–633 CrossRef CAS PubMed.
- K. Truong and M. Ikura, Curr. Opin. Struct. Biol., 2001, 11, 573–578 CrossRef CAS PubMed.
- H. Wallrabe and A. Periasamy, Curr. Opin. Biotechnol., 2005, 16, 19–27 CrossRef CAS PubMed.
- D. W. Piston and G. J. Kremers, Trends Biochem. Sci., 2007, 32, 407–414 CrossRef CAS PubMed.
- A. P. Alivisatos, W. Gu and C. Larabell, Annu. Rev. Biomed. Eng., 2005, 7, 55–76 CrossRef CAS PubMed.
- X. Chi, D. Huang, Z. Zhao, Z. Zhou, Z. Yin and J. Gao, Biomaterials, 2012, 33, 189–206 CrossRef CAS PubMed.
- A. R. Clapp, I. L. Medintz and H. Mattoussi, ChemPhysChem, 2006, 7, 47–57 CrossRef CAS PubMed.
- P. D. Howes, R. Chandrawati and M. M. Stevens, Science, 2014, 346, 1247390 CrossRef PubMed.
- K. E. Sapsford, L. Berti and I. L. Medintz, Angew. Chem., Int. Ed., 2006, 45, 4562–4588 CrossRef CAS PubMed.
- L. Yuan, W. Lin, K. Zheng and S. Zhu, Acc. Chem. Res., 2013, 46, 1462–1473 CrossRef CAS PubMed.
- C. Berney and G. Danuser, Biophys. J., 2003, 84, 3992–4010 CrossRef CAS PubMed.
- U. Noomnarm and R. M. Clegg, Photosynth. Res., 2009, 101, 181–194 CrossRef CAS PubMed.
- V. A. Azov, A. Schlegel and F. Diederich, Angew. Chem., Int. Ed., 2005, 44, 4635–4638 CrossRef CAS PubMed.
- V. A. Azov, A. Beeby, M. Cacciarini, A. G. Cheetham, F. Diederich, M. Frie, J. K. Gimzewski, V. Gramlich, B. Hecht, B. Jaun, T. Latychevskaia, A. Lieb, Y. Lill, F. Marotti, A. Schlegel, R. R. Schlittler, P. J. Skinner, P. Seiler and Y. Yamakoshi, Adv. Funct. Mater., 2006, 16, 147–156 CrossRef CAS.
- J. R. Moran, S. Karbach and D. J. Cram, J. Am. Chem. Soc., 1982, 104, 5826–5828 CrossRef CAS.
- I. Pochorovski, B. Breiten, W. B. Schweizer and F. Diederich, Chem.–Eur. J., 2010, 16, 12590–12602 CrossRef CAS PubMed.
- I. Pochorovski, T. Knehans, D. Nettels, A. M. Müller, W. B. Schweizer, A. Caflisch, B. Schuler and F. Diederich, J. Am. Chem. Soc., 2014, 136, 2441–2449 CrossRef CAS PubMed.
- I. Pochorovski and F. Diederich, Isr. J. Chem., 2012, 52, 20–29 CrossRef CAS.
- H. L. Kee, C. Kirmaier, L. Yu, P. Thamyongkit, W. J. Youngblood, M. E. Calder, L. Ramos, B. C. Noll, D. F. Bocian, W. R. Scheidt, R. R. Birge, J. S. Lindsey and D. Holten, J. Phys. Chem. B, 2005, 109, 20433–20443 CrossRef CAS PubMed.
- F. Li, S. I. Yang, Y. Ciringh, J. Seth, C. H. Martin, D. L. Singh, D. Kim, R. R. Birge, D. F. Bocian, D. Holten and J. S. Lindsey, J. Am. Chem. Soc., 1998, 120, 10001–10017 CrossRef CAS.
- L. Wang, I. S. Tamgho, L. A. Crandall, J. J. Rack and C. J. Ziegler, Phys. Chem. Chem. Phys., 2015, 17, 2349–2351 RSC.
- Y. Wang, D. Zhang, H. Zhou, J. Ding, Q. Chen, Y. Xiao and S. Qian, J. Appl. Phys., 2010, 108, 033520 CrossRef.
- E. Collini, C. Y. Wong, K. E. Wilk, P. M. G. Curmi, P. Brumer and G. D. Scholes, Nature, 2010, 463, 644–647 CrossRef CAS PubMed.
- P. D. Dahlberg, A. F. Fidler, J. R. Caram, P. D. Long and G. S. Engel, J. Phys. Chem. Lett., 2013, 4, 3636–3640 CrossRef CAS PubMed.
- G. S. Schlau-Cohen, A. Ishizaki and G. R. Fleming, Chem. Phys., 2011, 386, 1–22 CrossRef CAS.
- A. A. Bakulin, S. E. Morgan, T. B. Kehoe, M. W. B. Wilson, A. W. Chin, D. Zigmantas, D. Egorova and A. Rao, Nat. Chem., 2016, 8, 16–23 CrossRef CAS PubMed.
- D. Hayes, G. B. Griffin and G. S. Engel, Science, 2013, 340, 1431–1434 CrossRef CAS PubMed.
- C. C. Jumper, J. M. Anna, A. Stradomska, J. Schins, M. Myahkostupov, V. Prusakova, D. G. Oblinsky, F. N. Castellano, J. Knoester and G. D. Scholes, Chem. Phys. Lett., 2014, 599, 23–33 CrossRef CAS.
- V. A. Azov, B. Jaun and F. Diederich, Helv. Chim. Acta, 2004, 87, 449–462 CrossRef CAS.
- J.-B. Wang, Q.-Q. Wu, Y.-Z. Min, Y.-Z. Liu and Q.-H. Song, Chem. Commun., 2012, 48, 744–746 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian Inc., Wallingford, CT, 2009 Search PubMed.
- M. Cho, Chem. Rev., 2008, 108, 1331–1418 CrossRef CAS PubMed.
- I. Stiopkin, T. Brixner, M. Yang and G. R. Fleming, J. Phys. Chem. B, 2006, 110, 20032–20037 CrossRef CAS PubMed.
- A. Nitzan, Chemical dynamics in Condensed Phases: Relaxation, Transfer and Reactions in Condensed Molecular Systems, Oxford University Press, Oxford, New York, 2006 Search PubMed.
- P. Hamm and M. T. Zanni, Concepts and Methods of 2D Infrared Spectroscopy, Cambridge University Press, Cambridge, New York, 2011 Search PubMed.
- C. Wang, M. L. Flanagan, R. D. McGillicuddy, H. Zheng, A. R. Ginzburg, X. Yang, K. Moffat and G. S. Engel, Biophys. J., 2016, 111, 2125–2134 CrossRef CAS PubMed.
- E. E. Ostroumov, R. M. Mulvaney, R. J. Cogdell and G. D. Scholes, Science, 2013, 340(6128), 52–56 CrossRef CAS PubMed.
- J. A. Myers, K. L. M. Lewis, F. D. Fuller, P. F. Tekavec, C. F. Yocum and J. P. Ogilvie, J. Phys. Chem. Lett., 2010, 1, 2774–2780 CrossRef CAS.
- J. Dostal, B. Benesova and T. Brixner, J. Chem. Phys., 2016, 145, 124312 CrossRef PubMed.
- E. Thyrhaug, K. Zidek, J. Dostal, D. Bina and D. Zigmantas, J. Phys. Chem. Lett., 2016, 7, 1653–1660 CAS.
- H. Langhals, A. J. Esterbauer, A. Walter, E. Riedle and I. Pugliesi, J. Am. Chem. Soc., 2010, 132, 16777–16782 CrossRef CAS PubMed.
- Y. R. Khan, T. E. Dykstra and G. D. Scholes, Chem. Phys. Lett., 2008, 461, 305–309 CrossRef CAS.
- H. Sahoo, D. Roccatano, M. Zacharias and W. M. Nau, J. Am. Chem. Soc., 2006, 128, 8118–8119 CrossRef CAS PubMed.
- A. Muñoz-Losa, C. Curutchet, B. P. Krueger, L. R. Hartsell and B. Mennucci, Biophys. J., 2009, 96, 4779–4788 CrossRef PubMed.
- J. D. Spiegel, S. Fulle, M. Kleinschmidt, H. Gohlke and C. M. Marian, J. Phys. Chem. B, 2016, 120, 8845–8862 CrossRef CAS PubMed.
- D. Su, C. L. Teoh, L. Wang, X. Liu and Y. T. Chang, Chem. Soc. Rev., 2017, 46, 4833–4844 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sc00818c |
| ‡ These authors contributed equally to this work. |
| § Current address: Department of Chemistry, Stony Brook University, Stony Brook, NY 11794, USA. |
| This journal is © The Royal Society of Chemistry 2018 |