Benchmarking lithium amide versus amine bonding by charge density and energy decomposition analysis arguments

Abstract

Lithium amides are versatile C–H metallation reagents with vast industrial demand because of their high basicity combined with their weak nucleophilicity, and they are applied in kilotons worldwide annually. The nuclearity of lithium amides, however, modifies and steers reactivity, region- and stereo-selectivity and product diversification in organic syntheses. In this regard, it is vital to understand Li–N bonding as it causes the aggregation of lithium amides to form cubes or ladders from the polar Li–N covalent metal amide bond along the ring stacking and laddering principle. Deaggregation, however, is more governed by the Li←N donor bond to form amine adducts. The geometry of the solid state structures already suggests that there is σ- and π-contribution to the covalent bond. To quantify the mutual influence, we investigated [{(Me₂NCH₂)₂(C₄H₂N)}Li]₂ (1) by means of experimental charge density calculations based on the quantum theory of atoms in molecules (QTAIM) and DFT calculations using energy decomposition analysis (EDA). This new approach allows for the grading of electrostatic Li⁺N⁻, covalent Li–N and donating Li←N bonding, and provides a way to modify traditional widely-used heuristic concepts such as the −I and +I inductive effects. The electron density ρ(r) and its second derivative, the Laplacian ∇²ρ(r), mirror the various types of bonding. Most remarkably, from the topological descriptors, there is no clear separation of the lithium amide bonds from the lithium amine donor bonds. The computed natural partial charges for lithium are only +0.58, indicating an optimal density supply from the four nitrogen atoms, while the Wiberg bond orders of about 0.14 au suggest very weak bonding. The interaction energy between the two pincer molecules, (C₄H₂N)₂²⁻, with the Li₂²⁺ moiety is very strong (ca. −628 kcal mol⁻¹), followed by the bond dissociation energy (−420.9 kcal mol⁻¹). Partitioning the interaction energy into the Pauli (ΔE_Pauli), dispersion (ΔE_disp), electrostatic (ΔE_elstat) and orbital (ΔE_orb) terms gives a 71–72% ionic and 25–26% covalent character of the Li–N bond, different to the old dichotomy of 95 to 5%. In this regard, there is much more potential to steer the reactivity with various substituents and donor solvents than has been anticipated so far.

---

Introduction

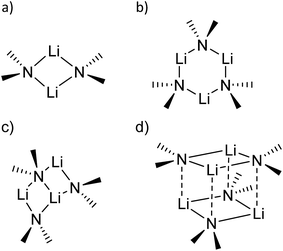
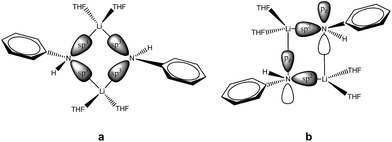
sec-Lithium amides (RR′NLi) have widespread applications as versatile reagents in synthetic inorganic and organic chemistry. This is because of the weak nucleophilicity of bulky lithium amides combined with a high basicity, making them excellent metallation reagents, even for vaguely acidic C–H bonds.¹ Furthermore, lithium amides can serve as catalysts, e.g. in the hydro-amination reaction, as described by Hultzsch et al.² Their reactivity is determined by their structure, which in turn is influenced by solvation, adjusting the aggregation.³ In 1971, Brown et al. had already investigated the aggregation of these lithium amide species.⁴ By recording NMR spectra of [LiN(SiMe₃)₂]_n at varied temperatures in several donor solvents, Collum et al. described an equilibrium between the monomeric and dimeric forms.⁵ Reich emphasized their importance in various mechanistic scenarios.⁶ In 1986, Snaith and Mulvey et al. described a similarity in the aggregation behaviour of alkyl lithium compounds and lithium amides.⁷ Therein, they stated that a Li₂N₂ four-membered ring acts as the central building block for further aggregation to form cubes or ladders, in line with the ring stacking and laddering principle (Scheme 1).⁸

Scheme 1 Examples of lithium amide solid state structures.

These frameworks were shown to depend on the degree of solvation and on the steric bulk of the amide, which was confirmed by Mulvey et al. in their deaggregation studies of lithium anilide,⁹ ultimately yielding the dimeric form containing the Li₂N₂ moiety as the smallest aggregate in tetrahydrofuran.¹⁰ During our research into the effects of group 14 metal coordination¹¹ by pincer type ligands,¹² we were able to obtain crystals of [{(Me₂NCH₂)₂(C₄H₂N)}Li]₂ (1), [{(C₄H₈NCH₂)₂(C₄H₂N)}Li]₂ (2) and [{(3,5-Me₂(C₅H₈N)NCH₂)₂(C₄H₂N)}Li]₂ (3) (Fig. 1). The crystal structures of 1 and 2 have been published earlier by Kuo et al.¹³ and Liu et al.,¹⁴ but the structure of 1 has so far only routinely been determined at room temperature.

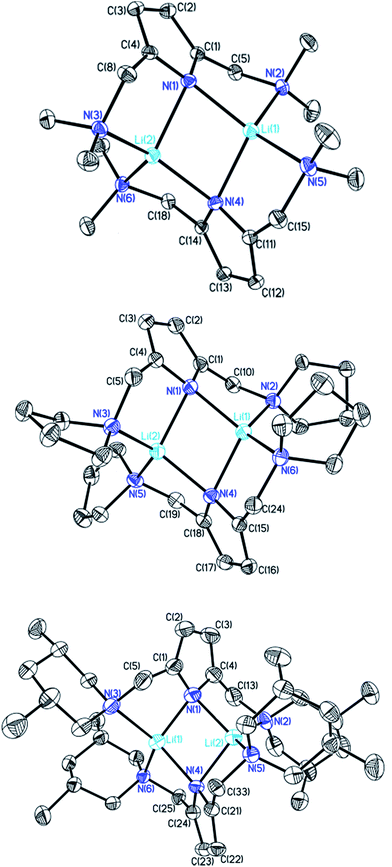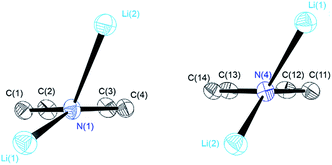
Fig. 1 Crystal structures of compounds 1 (top), 2 (centre) and 3 (bottom). Thermal ellipsoids are depicted at the 50% probability level, and hydrogen atoms have been omitted for clarity. Selected bond lengths and angles of 1 and 2 are shown in Table 1. Compound 3 shows severe disorder of the whole molecule, which makes it impossible to analyse bond lengths and angles in any serious detail.

Experimental charge density studies

The central Li₂N₂ four-membered ring, common to all three compounds, represents the smallest unit (cf.Scheme 1a) for the previously mentioned laddering and stacking of the higher lithium amide aggregates. A closer inspection of the structural features is therefore worthwhile and was embarked upon in the current paper by means of charge density investigations.¹⁵ The most striking feature of the geometries is the prominent asymmetry within the central Li₂N₂ four-membered rings. Table 1 summarizes the bond lengths and angles of the Li–N bonds. In 1, the bond distances within the central moiety differ by 0.08 Å, from 2.0363(3) Å to 2.1212(3) Å. In addition, the Li–N–Li angles in the range of 76° to 78° are remarkably acute. While the Li–N bonds at N4 only slightly differ (N4–Li1 = 2.0705(3) Å and N4–Li2 = 2.0363(3) Å), the difference at N1 is much more pronounced (N1–Li1 = 2.0460(3) Å and N1–Li2 = 2.1212(3) Å). Furthermore, in a view with the pyrrole rings in the plane, it is evident that one lithium atom is closer to that ring plane than the other (see Fig. 2). The distances of the two lithium atoms to the plane containing N4 are relatively similar, and Li2 is only slightly closer to the plane ((N4 plane)⋯Li2 = 0.924 Å and (N4 plane)⋯Li1 = 1.298 Å). The difference is much more pronounced for the plane including N1. Li1 is much closer to the plane than Li2 ((N1 plane)⋯Li1 = 0.559 Å and (N1 plane)⋯Li2 = 1.522 Å). This asymmetric bonding geometry was already found earlier by us for primary amides. We attributed the widespread structural features to re-hybridization at the nitrogen atom from sp³ to sp² (Scheme 2). Different to this, sp³ hybridized amidic nitrogen atoms with equally populated hybrid orbitals should give Li–N–Li bond angles close to 109° and equilateral Li₂N₂ four-membered rings, with the two substituents at the nitrogen atom located at the Li–N–Li bisection (Scheme 2a). An sp² hybridization should give rise to a more distorted geometry.

Table 1 Geometry at N1 and N4 in 1 with the pyrrolyl moiety orthogonal to the paper plane. Values given in parentheses are taken from theoretical calculations (BP86+D3(BJ)/def2-TZVPP) which are described below

Bond lengths (Å) and angles (°)	1		2
N1–Li1	2.0460(3)	(2.029)	2.019(2)	(2.017)
N1–Li2	2.1212(3)	(2.029)	2.083(2)	(2.039)
N4–Li1	2.0705(3)	(2.029)	2.073(2)	(2.020)
N4–Li2	2.0363(3)	(2.029)	2.013(2)	(2.031)
Li1–N1–Li2	76.468(12)	(75.9)	76.32(9)	(76.5)
Li1–N4–Li2	77.822(12)	(75.9)	76.67(9)	(76.6)

---

Fig. 2 Geometry at N1 and N4 in 1 with the pyrrolyl moiety orthogonal to the paper plane.

Scheme 2 Possible orbital interactions within the Li₂N₂ four-membered ring building block of lithium amides.

A shorter Li–N σ-bond is formed by the sp² hybrid orbital within the plane of the amide, while the corresponding non-hybridized remaining p-orbital is involved with the longer Li–N bond towards the second lithium atom within the dimer. Obviously, this lithium atom is most dislocated from the amide plane when the p-orbital is involved in any Li–N bonding. As the pyrrolyl nitrogen atom in 1 is unequivocally sp² hybridized, we anticipated bonding similar to that in Scheme 2b.

To check whether or not this asymmetry is a common motif in dimeric lithium amide structures, an extensive search in the Cambridge Structural Database (CSD)¹⁶ for all structures with a Li₂N₂ unit, not containing more than two lithium atoms, was carried out. 155 structures were found in version 5.37 of the CSD. For each nitrogen atom, d₁ and d₂ represent the two bond distances to lithium atoms 1 and 2, while d₃ and d₄ are calculated as the distances of lithium atoms 1 and 2 to the plane containing the nitrogen atom and its two next non-metallic bonding partners (see Fig. 4).

Fig. 3 Molecular graphs for 1, (a) derived from experiment and (b) derived from theoretical calculations at the BP86+D3(BJ)/def2-TZVPP level of theory. Bond critical points are marked in red and ring critical points in yellow.

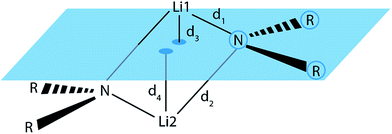Fig. 4 Definition of the Li–N bond distances, d₁ and d₂, and the distances d₃ and d₄ from the lithium atoms to the RNR plane.

For the bonding situation outlined in Scheme 2b, we expect d₁ and d₂ to differ and the lithium atom with the shorter Li–N distance to be closer to the nitrogen plane. The latter would cause the differences d₁ − d₂ and d₃ − d₄ to have the same sign. Therefore, we plotted d₁ − d₂ against d₃ − d₄ (cf.Fig. 4). The correlation between these two values is calculated to be 0.491, and 118 data points (blue) fulfil our expectations while 37 (red) disagree (Fig. 5).

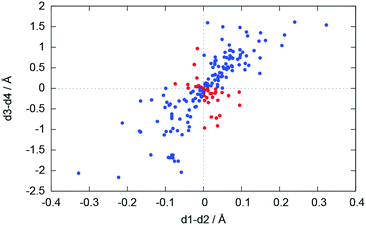Fig. 5 Plot of d₁ − d₂vs. d₃ − d₄. Blue dots represent database entries which are in agreement with the structure in Scheme 2b, and red dots represent entries which disagree.

The nature of the Li–N bonds has also been the subject of several theoretical studies, mainly attributing purely¹⁷ or mostly ionic^18–20 character to the bond. Following the idea of Maddaluno and Silvi et al.,¹⁷ who analysed lithium dimethyl amide as well as its dimer and related compounds within the ELF framework, a purely ionic interaction of a lithium cation with an sp³ hybridized nitrogen atom would result in identical bond lengths for all Li–N bonds in the dimeric species (cf.Scheme 2a).

Using population analysis, Schleyer, Pople et al.²⁰ and Reed et al.¹⁹ proposed a more covalent bonding model for the monomeric lithium amide LiNH₂ with a significant π overlap population for the lithium–nitrogen bond. This would imply sp² hybridization at the nitrogen atom.⁹ Bonding like this would most likely result in the geometry proposed in Scheme 2b and is found for 71.5% of the Li₂N₂ entities in our CSD search. One lithium atom is located closer to the nitrogen atom and closer to the plane spanned by the nitrogen atom and the two non-metallic substituents (Scheme 2b).

To shed light on the nature of these lithium–nitrogen bonds from an experimental point of view, we recorded a high-resolution data set for 1. The unambiguous hybridization state of the bridging nitrogen atoms in 1 and the additionally present tertiary amine donor sites present an ideal starting point for this study.

The Hansen–Coppens multipole formalism²¹ was applied and the electron density (ED) of 1 was subsequently analysed within the quantum theory of atoms in molecules (QTAIM) framework.²² As the QTAIM framework is also applicable to EDs from theoretical calculations, we can complement our experimental results with results obtained from theory (for details regarding the theoretical calculations or the experimental details, see the ESI†).

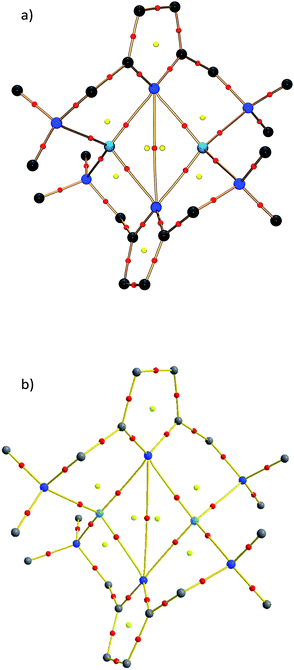
Within the QTAIM framework, a bonding interaction is linked to the existence of a line of maximum electron density ρ(r) (bond path)²³ and of the atomic basins enclosed by so-called zero-flux surfaces. The minimum value of ρ along the bond path is called the bond critical point (BCP). Along with other critical points defining rings (ring critical point, RCP) and cages (cage critical point, CCP), this builds the first step towards describing the topology of molecules. The entirety of the critical points is described by the Poincaré–Hopf equation,²⁴ which is fulfilled for both the theoretical and the experimental studies (see Fig. 6; for a full list of critical points including values of ρ(r) and ∇²ρ(r), see the ESI†). Both the experimental and theoretical molecular graphs show all of the expected features.²⁵

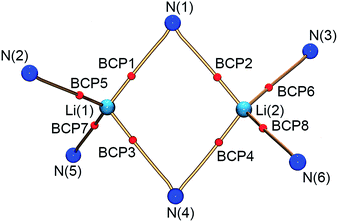Fig. 6 Molecular graph of the central Li₂N₂ ring and the amine nitrogen–lithium interactions (red spheres indicate bond critical points).

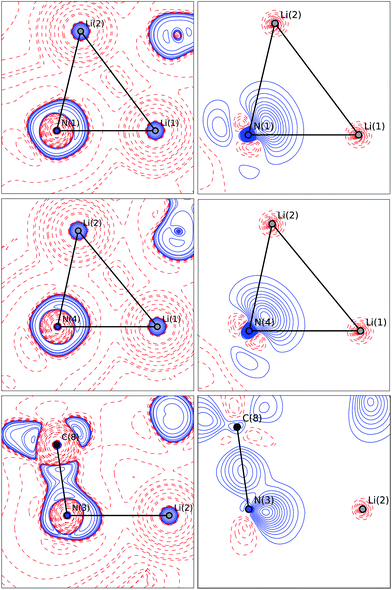
The bonding situation in the central Li₂N₂ ring is best described in terms of ρ(r) and its second derivative, the Laplacian ∇²ρ(r). The Laplacian of the electron density indicates the local charge density concentrations (negative values of ∇²ρ(r)) and charge density depletions (positive values). Fig. 6 shows the found lithium–nitrogen bond paths obtained from the experimental structure. The bond critical points are in all cases shifted towards the more electropositive lithium atom. The results from theory exhibit the same features (see the ESI for details†). As can be seen from Table 2, the values of ρ(r) are minute, while ∇²ρ(r) adopts a positive sign. This is indicative of the considerably polarized bonds within the QTAIM. However, BCP1 and 4 exhibit slightly higher values in both ρ(r) and ∇²ρ(r). Also evident from Table 2 is the fact that the bond lengths, as well as the values for ρ(r) and ∇²ρ(r) at BCP2, lie closer to the values observed for the amine nitrogen atoms in the periphery (BCP5–BCP8). However, from the topological descriptors, there is no clear separation of the lithium amide bonds from the lithium amine donor bonds. So ρ(r) and ∇²ρ(r) at the bond critical point seem to be more dependent on the bond lengths than on the hybridization state. This further emphasizes the predominant electrostatic nature of any lithium–nitrogen bond, regardless of the level of σ, π or donor contribution.

Table 2 Bond length (d), electron density ρ(r) and Laplacian ∇²ρ(r) values at BCP1–8 (for numbering, refer to Fig. 6). Estimated standard deviations for ρ(r) were taken from the XD2006 program suite,²⁶ while for ∇²ρ(r) they were taken from the method proposed by Krause et al.²⁷

		d/Å	Experimental		Theoretical^a
			ρ(r)/eÅ^−3	∇^2ρ(r)/eÅ^−5	ρ(r)/eÅ^−3	∇^2ρ(r)/eÅ^−5
a Electron density computed at the BP86+D3(BJ)/def2-TZVPP level of theory on the frozen experimental geometry.
BCP1	Li1–N1	2.0460(3)	0.139(1)	4.085(10)	0.184	3.891
BCP2	Li2–N1	2.1212(3)	0.116(1)	3.254(7)	0.148	3.113
BCP3	Li1–N4	2.0705(3)	0.132(1)	3.784(8)	0.171	3.588
BCP4	Li2–N4	2.0363(3)	0.148(1)	4.195(7)	0.187	3.956
BCP5	Li1–N2	2.1165(3)	0.122(1)	3.557(6)	0.162	3.266
BCP6	Li2–N3	2.1169(3)	0.121(1)	3.549(5)	0.163	3.227
BCP7	Li1–N5	2.1315(3)	0.116(1)	3.404(5)	0.157	3.113
BCP8	Li2–N6	2.1033(3)	0.126(1)	3.687(5)	0.168	3.389

---

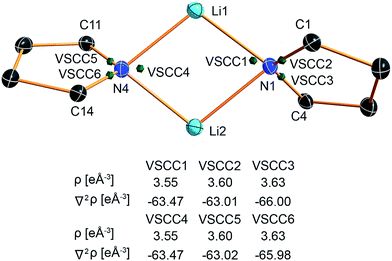
The valence shell charge concentrations (VSCCs) are critical points in the Laplacian. Two types of VSCC can be distinguished: bond- and non-bond-directed ones. The non-bond-directed VSCCs are typically associated with regions where lone pairs are expected. For 1, three VSCCs at the nitrogen N1 and N4 atoms are anticipated and confirmed: two bonded VSCCs facing the adjacent carbon atoms, and one non-bonded VSCC. The non-bonded VSCC at N1 is almost directly facing Li1, indicating that the highest charge concentration along the Li1–N1 path is directed away from Li2, consistent with the smallest values for ρ(r) and ∇²ρ(r) at the BCP of the longest Li–N distance in the molecule. In contrast, the VSCC of N4 is directed towards the Li1–N4–Li2 bisector (cf.Fig. 7), consistent with the smaller difference of the bond lengths Li1–N4 and Li2–N4. From this, N1 more closely mimics the bonding situation in Scheme 2b, while N4 is more similar to the dual bisecting bonding in Scheme 2a. In Fig. 8, plots of the deformation density and the Laplacian of the electron density for N1, N4 and N3 are shown. In the plots of ∇²ρ(r), the same tendency as discussed previously can be seen. The region of maximum charge density concentration is, for N1, shifted towards Li1. The same is true for the deformation density of N1 and N4. However, the differences are less pronounced compared to the Laplacian. Both of the nitrogen atoms however show the typical signs of sp² hybridisation. This is especially evident when compared to the sp³ hybridized nitrogen atom N3 (Fig. 8, bottom).

Fig. 7 Positions of the valence shell charge concentrations (VSCCs) at N1 and N4.

Fig. 8 Plots of the Laplacian ∇²ρ(r) (left column) and the deformation density (right column) for the pyrrole nitrogen atoms (top and middle) and an amine nitrogen atom (bottom). Blue contours indicate lines of constant values, and red contours indicate negative ones. Contour lines are displayed at levels of 1ⁿ, 2ⁿ, 4ⁿ and 8ⁿ eÅ⁻⁵, with n = −2, −1, 0, 1, 2, 3 and 4 for the Laplacian (left) and −0.9 to 0.9 eÅ⁻³ in steps of 0.05 eÅ⁻³ for the deformation density (right).

Computational investigations

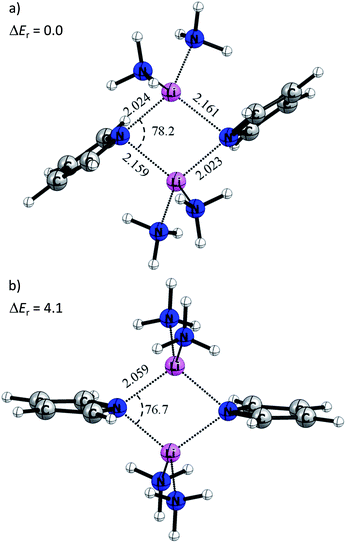
Quantum chemical calculations at the BP86+D3(BJ)/def2-TZVPP level of theory have been carried out to gain more insight into the electronic structure and the various energy contributions in these compounds (computational details are in the ESI†). Table 1 shows selected bond lengths and angles of the cyclic Li₂N₂ core of the calculated equilibrium structures of 1 and 2. In general, the theoretical values agree that the gas-phase optimized structure is predicted to be symmetric with N–Li bond distances of 2.029 Å, while compound 2 shows reduced asymmetry compared that determined experimentally, i.e. 2.017 Å (or 2.020 Å) and 2.039 Å (or 2.031 Å).

This difference indicates that the asymmetry observed in the X-ray structures might be induced by the solid state arrangement restraining the flat potential energy surface. In order to understand the origins of the Li–N bond length differences, a model system where the methylene bridges of the pincer ligands were omitted was used (4^M). In this case, the pyrrole ring is not attached to any amine groups. The amine donors would not superimpose their steric requirements on the overall structure, providing maximum flexibility.

Fig. 9a displays the optimized structure of 4^M without any symmetry constraints. Clearly, the structure is similar to the situation described in Scheme 2b. The lone pairs on the sp² orbital of the pyrrole nitrogen are pointing toward the lithium atoms, giving a strong interaction and a Li–N distance of 2.023 Å, while the p_z lone pair gives a weaker interaction with a Li–N bond length of 2.161 Å. It is noteworthy that the ammonia molecules retain a similar position, like the donating side-arms in complexes 1 and 2. We also optimized the model systems (5^M) with a D_2h symmetry constraint (Fig. 9b). Here the pyrrole rings mimic the ideal geometry in Scheme 2a. The computed energy difference (ΔE_r) between 4^M and 5^M is 4.1 kcal mol⁻¹. This relatively low energy penalty can then be easily compensated by the methylene-bridged N-donors.

Fig. 9 Optimized BP86+D3(BJ)/def2-TZVPP molecular structure of the model system, (a) without constraints (4^M) and (b) with D_2h symmetry (5^M). Bond distances and angles are in Å and °, respectively. The relative energy ΔE_r is in kcal mol⁻¹.

Fig. 10 shows the most important molecular orbitals of 1 (for an extended list of molecular orbitals, see the ESI†). As expected, the nitrogen atoms adopt sp² hybridization (HOMO−9 and HOMO−8) where p_z is compromised with the ring π system (HOMO−3 and HOMO−2). The molecular orbitals suggest that there is a donation of electron density from the nitrogen atoms to the lithium atoms. Indeed, the computed natural partial charges (in Table 3) are around +0.58 electrons. However, the Wiberg bond orders suggest a very weak bonding character.

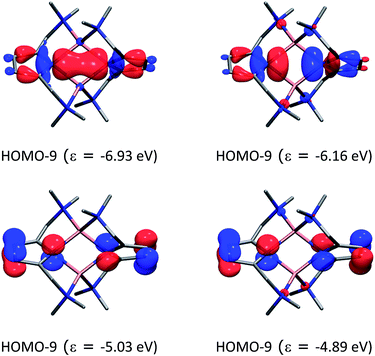Fig. 10 Molecular orbitals of compound 1 and their energies (in eV) at the BP86+D3(BJ)/def2-TZVPP level of theory. The hydrogen atoms were omitted for clarity.

Table 3 NBO partial charges (Q) and Wiberg bond orders (P) at BP86+D3(BJ)/def2-TZVPP

Q or P	1	2
Q(Li1)	+0.58	+0.59
Q(Li2)	+0.58	+0.54
Q(N1)	−0.61	−0.61
Q(N2) and Q(N3)	−0.43	−0.43
Q(N4)	−0.68	−0.61
Q(N5) and Q(N6)	−0.43	−0.43
P(Li–Li)	0.06	0.06
P(Li1–N1)	0.14	0.14
P(Li2–N1)	0.14	0.12
P(Li1–N4)	0.14	0.15
P(Li2–N4)	0.14	0.13
P(Li1–N2) and P(Li1–N5)	0.08	0.07
P(Li2–N3) and P(Li2–N6)	0.08	0.08

---

Energy decomposition analysis (EDA) was performed in order to unravel the nature of the interaction between the Li atoms and the pincer molecules.²⁸ EDA has proven to be a powerful tool for improving the understanding of chemical bonding in main group compounds and transition metal compounds.²⁹ Within this method, the bond formation between two or more interacting fragments is divided into three steps (for further details, see the ESI†). In the first step, the fragments, which are calculated using the frozen geometries within the entire molecule, are placed into the molecule disposition without electronic relaxation to yield the electrostatic interaction (ΔE_elstat). In the second step, the wave function is anti-symmetrized and re-normalized giving the Pauli repulsion within the fragments (ΔE_Pauli). In the third step, the molecular orbitals relax into the final state to yield the stabilizing orbital term (ΔE_orb). Also, the stabilizing dispersion interaction can be computed (ΔE_disp). The sum of all the terms gives the total interaction energy ΔE_int. The dissociation energy can be calculated by combining the interaction energy together with the preparation energy (ΔE_prep), which is the energy needed to promote the fragments from their equilibrium geometry to the geometry and electronic state in the compounds. Notably, in the present system, many fragmentation schemes can be envisioned to form 1 and 2. We performed EDA calculations to select the fragments (C₄H₂N)₂²⁻ and Li₂²⁺ as the interaction can be cleanly evaluated. The numerical results are presented in Table 4.

Table 4 Energy decomposition analysis (EDA-NOCV) of 1 and 2 at the BP86+D3(BJ)/TZ2P+ level. The fragments were (C₄H₂N)₂²⁻ and Li₂²⁺, and energy values are given in kcal mol⁻¹

	1	2
a The value in parentheses gives the percentage contribution to the total attractive interactions, ΔEelstat + ΔEorb + ΔEdisp. b The value in parentheses gives the percentage contribution to the total orbital interactions ΔEorb.
ΔEint	−627.5	−630.4
ΔEPauli	71.7	71.2
ΔEdisp^a	−18.1 (2.6)	−19.7 (2.8)
ΔEelstat^a	−502.5 (71.9)	−499.5 (71.2)
ΔEorb^a	−178.5 (25.5)	−182.4 (26.0)
ΔEorbρ(1)^b	−19.7 (11.0)	−21.3 (11.7)
ΔEorbρ(2)^b	−20.3 (11.4)	−19.7 (11.0)
ΔEorbρ(3)^b	−16.5 (9.2)	−16.1 (9.0)
ΔEorbρ(4)^b	−15.2 (8.5)	−13.9 (7.8)
ΔEorbρ(5)^b	−14.4 (8.1)	−14.0 (7.8)
ΔEorbρ(6)^b	−14.1 (7.9)	−12.4 (6.9)
ΔEorbρ(7)^b	−11.0 (6.2)	−10.4 (5.8)
ΔEorbρ(8)^b	−8.4 (4.7)	−7.7 (4.3)
ΔEorbρrest^b	−58.9 (33.0)	−66.9 (37.5)
ΔEprep	211.5	209.5
−De = ΔE	−416.0	−420.9

---

The interaction energy between the two pincer molecules, (C₄H₂N)₂²⁻, with the Li₂²⁺ moiety is very strong, i.e. −627.5 and −630.4 kcal mol⁻¹ for compounds 1 and 2, respectively. The bond dissociation energy (D_e) follows the same trend, being −416.0 for 1 and −420.9 kcal mol⁻¹ for 2. The preparation energy (ΔE_prep) is important in order to take into account the energy required to bring together on the one hand the two positively charged lithium atoms, and on the other hand the two negatively charged pincers. Interestingly, splitting the interaction term into the dispersion (ΔE_disp), electrostatic (ΔE_elstat) and orbital (ΔE_orb) terms gives relevant information. The bond interaction is around 71–72% ionic and 25–26% covalent, which gives a different perspective to the old dichotomy.^7,8 The dispersion is minute and only 2% of the stabilizing contributions. Although not the strongest contribution, the covalent contribution (ΔE_orb) is pronounced in absolute numbers by ca. −180.0 kcal mol⁻¹. This is in good agreement with the presence of the bond paths found by QTAIM analysis.

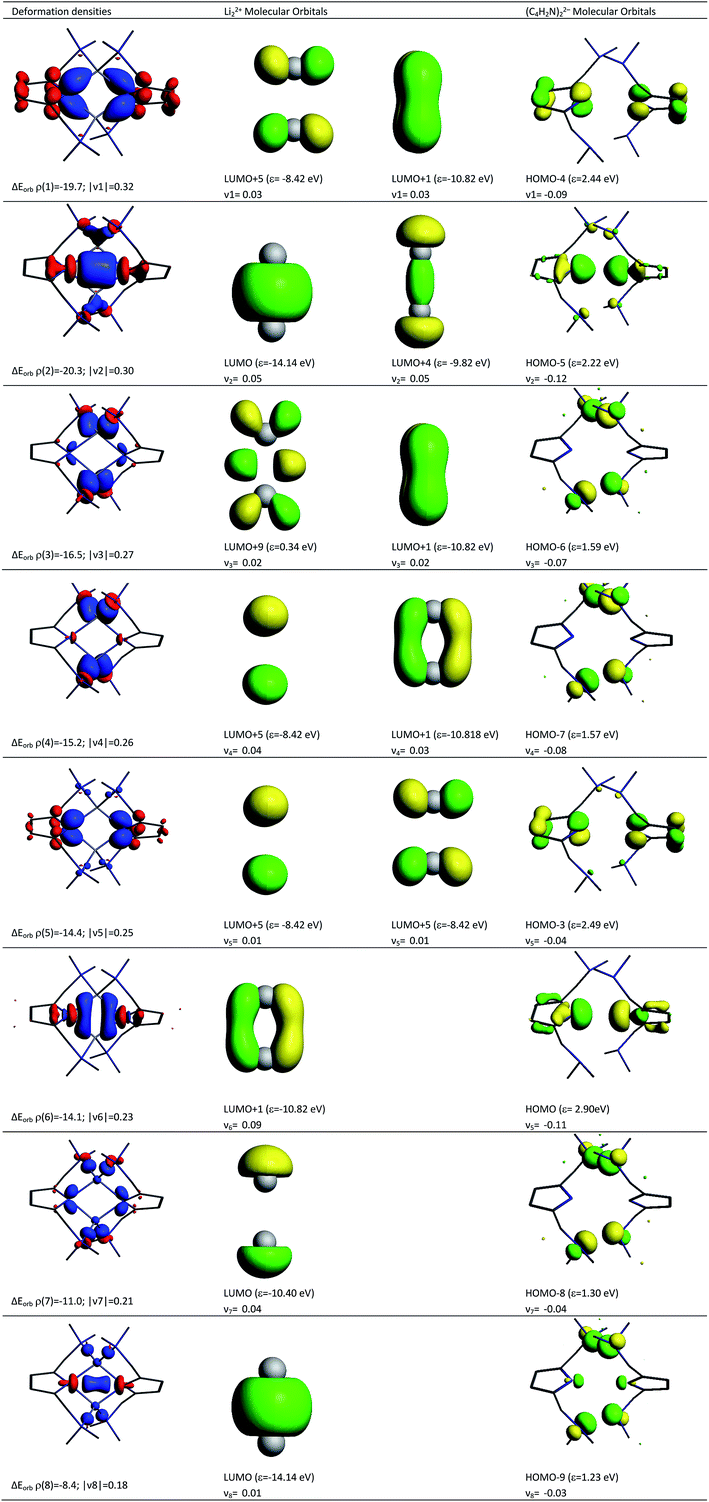
Deeper insights into the nature of the covalent interaction are available from EDA in combination with natural orbitals for chemical valence calculations (EDA-NOCV).³⁰ This method deconstructs the orbital term (ΔE_orb) into components (ΔE_orbρ(i)) that provide an energetic estimation of a given deformation density (ρ(i)), which is related to a particular electron flow channel, and consequently the amount of charge transferred, Δq(i) = |ν(i)|, for the bonding between the interacting fragments. Table 4 summarizes the strongest eight contributions to the orbital term. It can be seen that the values of the orbital terms are the results of several small contributions where the strongest is only slightly above −20 kcal mol⁻¹. The deformation densities of 1, which are associated with the orbital interactions, are shown in the first column of Fig. 11 (see Fig S5† for those of 2). The colour coding (red → blue) illustrates the direction of charge flow. A nice feature of the EDA-NOCV method is that it not only provides numerical results, but also that the change in the electronic structure, which is associated with the orbital interactions, can be visualized. The eigenvalues ν1–ν8 are a measure of the size of the charge alteration, which does always correlate with the strength of the orbital interactions. The second and third column of Fig. 11 display the orbitals of the fragments, responsible for each deformation density, and the amount of electrons which are donated.

Fig. 11 Plot of the deformation densities, Δρ (isovalue = 0.001 a.u.), of the pairwise orbital interactions between Li₂²⁺ and (C₄H₂N)₂²⁻ within compound 1. ΔE denotes associated energies (in kcal mol⁻¹) and ν denotes eigenvalues (in a.u.). The red colour shows the charge outflow, whereas blue shows charge density accumulation. The shapes of the most important interacting occupied and vacant orbitals (isovalue = 0.06 a.u.) of the fragments are shown.

According to the data in Fig. 11, four of the contributions result from the donation of lone pairs from the amine atoms of the pincer side arms into the empty orbitals of the lithium system, such as ρ(3), ρ(4), ρ(7) and ρ(8). The resulting deformation densities are the four different combinations possible for the lone pairs. The corresponding energies are not very high (ΔE_orb = 16.5–8.4 kcal mol⁻¹) and the charge flows associated are not significant (|ν(i)| = 0.27–0.18). This is expected for interactions with a weak covalent character. Interestingly, the sp² lone pairs of the pyrrole nitrogen atoms can be distinguished as two clear contributions. On the one hand, ρ(2) comes from the positive combination of the lone pairs (+, +) which interact with the empty σ orbital between the Li atoms. On the other hand, ρ(6) shows a charge flow of a (+, −) contribution into the vacant π system of Li₂²⁺. The main list of orbital terms of EDA-NOCV is completed by the interaction of the p_z orbitals at the pyrrole nitrogen atoms associated with ρ(1) and ρ(5). ρ(1) is the p_z (+, −) orbital combination which interacts with the π* orbitals of Li₂²⁺ and presents a strong orbital term energy ΔE_orb of ρ(1) = −19.7 kcal mol⁻¹. The ρ(5) is associated to the interaction to the (+, −) p_z orbitals of pyrrole ring orbitals and the π* orbitals of Li₂²⁺. The deformation densities ρ(1), ρ(2), ρ(5) and ρ(6) suggest a strong polarization within the pyrrole rings as well as an accumulation of electron density between these N atoms and the Li cations, supporting the QTAIM model presented in Fig. 3.

Conclusions

The current paper opens up the avenue to gradually modify the aggregation and hence the reactivity of lithium amides in a N-donating environment. We deconvoluted the polar Li–N covalent metal amide bonds from the Li←N amine donor bonds in [{(Me₂NCH₂)₂(C₄H₂N)}Li]₂ (1). σ- and π-bonding contributes to the covalent bond. The combination of experimental charge density investigations based on the quantum theory of atoms in molecules (QTAIM) and DFT based on energy decomposition analysis (EDA) facilitates the quantification of either energy share. The electron density ρ(r) and its second derivative, the Laplacian ∇²ρ(r), recover the molecular graph and mirror the asymmetry in the Li₂N₂ four-membered ring. Most remarkably, from the topological descriptors, there is no clear separation of the lithium amide bonds from the lithium amine donor bonds. The computed natural partial charges for lithium are only +0.58, indicating an optimal density supply from the four nitrogen atoms, while the Wiberg bond orders of about 0.14 suggest very weak bonding. The interaction energy between the two (C₄H₂N)₂²⁻ pincer molecules and the Li₂²⁺ moiety is very strong (ca. −628 kcal mol⁻¹), followed by the bond dissociation energy (−420.9 kcal mol⁻¹). Partitioning the interaction term into the dispersion (ΔE_disp), electrostatic (ΔE_elstat) and orbital (ΔE_orb) terms gives a 71–72% ionic and 25–26% covalent character of the Li–N bond, different to the old dichotomy of 95 to 5%. The latter left only a little space and motivation for modifying covalent Li–N bonding and hence aggregation and reactivity. Knowing now that the bonding capacity of a neutral amine is on par with the amide donor bond pushes the door wide open to grade ionic Li⁺N^–, covalent Li–N and donating Li←N bonding in connection to σ- and π-bonding by substituent and solvent permutation. We are currently trying to identify a benchmark protocol in organic synthesis to scale the various bonding features with different levels of reactivity.

Experimental details

Shock cooled crystals were selected from a Schlenk flask under argon atmosphere using the X-TEMP2 device.³¹ The data were collected on a Bruker D8 Ultra diffractometer equipped with a molybdenum Turbo X-ray Source (TXS) rotating anode generator and INCOATEC Helios mirror optics and integrated with SAINT.³² A multi-scan absorption correction (SADABS) was applied.³³ The structures were solved by direct methods (SHELXT)³⁴ and refined on F² using the full-matrix least-squares methods of SHELXL³⁵ within the SHELXLE GUI.³⁶ Multipole model refinement was carried out with the XD2006 program suite.²⁶ The data were corrected for resolution- and temperature-dependent errors using the method of Niepötter et al.³⁷ To obtain the best refinement strategy, the cross-validation method proposed by Krause et al. was employed.²⁷ More details about the crystallographic data and the refinement can be found in the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Thanks to the Danish National Research Foundation (DNRF93) funded Centre for Materials Crystallography (CMC) for partial support and the federal state of Lower Saxony, Germany for providing a fellowship in the CaSuS PhD program.

Notes and references

1. (a) M. F. Lappert, Metal and metalloid amides, Ellis Horwood, Chichester, 1980; (b) B. J. Wakefield, Organolithium methods, Academic Press, London, 2nd edn, 1994; (c) R. Neufeld, M. John and D. Stalke, Angew. Chem. Int. Ed., 2015, 54, 6994–6998 ( Angew. Chem. , 2015 , 127 , 7100–7104 ); (d) R. Neufeld, R. Michel, R. Herbst-Irmer, R. Schöne and D. Stalke, Chem.−Eur. J., 2016, 22, 12340; (e) T. Rathman and J. Schwindeman, Org. Process Res. Dev., 2014, 18, 1192; (f) R. E. Mulvey and S. D. Robertson, Angew. Chem. Int. Ed., 2013, 52, 11470 ( Angew. Chem. , 2013 , 125 , 11682–11700 ); (g) E. Carl and D. Stalke, Structure-Reactivity Relationship in Organolithium Compounds, in Lithium Compounds in Organic Synthesis – From Fundamentals to Applications, ed. R. Luisi and V. Capriati, Wiley-VCH, Weinheim 2014, pp. 1–31.
2. P. H. Martínez, K. C. Hultzsch and F. Hampel, Chem. Commun., 2006, 2221.
3. M. F. Lappert, M. J. Slade, A. Singh, J. L. Atwood, R. D. Rogers and R. Shakir, J. Am. Chem. Soc., 1983, 105, 302.
4. B. Y. Kimura and T. L. Brown, J. Organomet. Chem., 1971, 26, 57.
5. (a) P. Zhao and D. B. Collum, J. Am. Chem. Soc., 2003, 125, 14411; (b) B. L. Lucht and D. B. Collum, Acc. Chem. Res., 1999, 32, 1035; (c) T. F. Briggs, M. D. Winemiller, D. B. Collum, R. L. Parsons, A. H. Davulcu, G. D. Harris, J. M. Fortunak and P. N. Confalone, J. Am. Chem. Soc., 2004, 126, 5427; (d) G. J. Reyes-Rodríguez, R. F. Algera and D. B. Collum, J. Am. Chem. Soc., 2017, 139, 1233; (e) P. F. Godenschwager and D. B. Collum, J. Am. Chem. Soc., 2007, 129, 12023.
6. H. J. Reich, Chem. Rev., 2013, 113, 7130.
7. D. R. Armstrong, D. Barr, W. Clegg, R. E. Mulvey, D. Reed, R. Snaith and K. Wade, J. Chem. Soc., Chem. Commun., 1986, 869.
8. K. Gregory, P. v. R. Schleyer and R. Snaith, Adv. Inorg. Chem., 1991, 37, 47.
9. R. v. Bülow, H. Gornitzka, T. Kottke and D. Stalke, Chem. Commun., 1996, 37, 1639.
10. W. Clegg, L. Horsburgh, F. M. Mackenzie and R. E. Mulvey, J. Chem. Soc., Chem. Commun., 1995, 111, 2011.
11. C. Maaß, D. M. Andrada, R. A. Mata, R. Herbst-Irmer and D. Stalke, Inorg. Chem., 2013, 52, 9539.
12. (a) C. J. Moulton and B. L. Shaw, J. Chem. Soc., Dalton Trans., 1976, 1020; (b) G. van Koten, J. T. B. H. Jastrzebski, J. G. Noltes, A. L. Spek and J. C. Schoone, J. Organomet. Chem., 1978, 148, 233.
13. P.-C. Kuo, J.-C. Chang, W.-Y. Lee, H. M. Lee and J.-H. Huang, J. Organomet. Chem., 2005, 690, 4168.
14. Q. Liu, Z. Guo, H. Han, H. Tong and X. Wei, Polyhedron, 2015, 85, 15.
15. (a) Electron Density and Chemical Bonding I. Experimental Charge Density Studies, ed. D. Stalke, Springer Berlin Heidelberg, Berlin, Heidelberg, 2012, vol. 146; (b) Electron Density and Chemical Bonding II. Theoretical Charge Density Studies, ed. D. Stalke, Springer Berlin Heidelberg, Berlin, Heidelberg, 2012, vol. 147; (c) D. Stalke, Chem.−Eur. J., 2011, 17, 9264; (d) The chemical bond. Fundamental aspects of chemical bonding, ed. G. Frenking and S. S. Shaik, Wiley-VCH Verlag, Weinheim, 2014; (e) The Chemical Bond. Chemical Bonding Across the Periodic Table, ed. G. Frenking and S. S. Shaik, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2014; (f) C. Gatti and P. Macchi, Modern Charge-Density Analysis, Springer, Netherlands, s. l, 1st edn, 2012.
16. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171.
17. C. Fressigné, J. Maddaluno, C. Giessner-Prettre and B. Silvi, J. Org. Chem., 2001, 66, 6476.
18. (a) J. B. Collins and A. Streitwieser, J. Comput. Chem., 1980, 1, 81; (b) D. R. Armstrong, D. Barr, W. Clegg, S. M. Hodgson, R. E. Mulvey, D. Reed, R. Snaith and D. S. Wright, J. Am. Chem. Soc., 1989, 111, 4719; (c) E. U. Wuerthwein, K. D. Sen, J. A. Pople and P. v. R. Schleyer, Inorg. Chem., 1983, 22, 496; (d) A. Hinchliffe and J. Charles Dobson, Theor. Chim. Acta, 1975, 39, 17; (e) A. L. Hinde, A. Pross and L. Radom, J. Comput. Chem., 1980, 1, 118; (f) A. Hinchliffe, Chem. Phys. Lett., 1977, 45, 88.
19. A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735.
20. J. D. Dill, P. v. R. Schleyer, J. S. Binkley and J. A. Pople, J. Am. Chem. Soc., 1977, 99, 6159.
21. (a) N. K. Hansen and P. Coppens, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1978, 34, 909; (b) P. Coppens, X-ray charge densities and chemical bonding, International Union of Crystallography, Chester, England, Oxford, New York, 1997, vol. 4.
22. R. F. W. Bader, Atoms in molecules. A quantum theory, Clarendon Press, Oxford, 2003, vol. 22.
23. (a) R. F. W. Bader, J. Phys. Chem. A, 1998, 102, 7314; (b) A. M. Pendás, E. Francisco, M. A. Blanco and C. Gatti, Chem.−Eur. J., 2007, 13, 9362.
24. H. Hopf, Math. Ann., 1927, 96, 209.
25. In fact, we were also able to observe a bond path linking N(1) and N(4). This will not be discussed because of the very small value and the close vicinity of the RCPs, which indicates that this geometry is close to a catastrophe point where these critical points coincide.³⁸ However, these kinds of BCP are not uncommon. Stalke et al.³⁹ as well as Zhurova et al.⁴⁰ already reported on trans annular N⋯N interactions.
26. A. Volkov, P. Macchi, L. J. Farrugia, C. Gatti, P. Mallinson, T. Richter and T. Koritsanszky, XD2006, 2006.
27. L. Krause, B. Niepötter, C. J. Schürmann, D. Stalke and R. Herbst-Irmer, IUCrJ, 2017, 4, 420.
28. (a) K. Morokuma, J. Chem. Phys., 1971, 55, 1236; (b) T. Ziegler and A. Rauk, Inorg. Chem., 1979, 18, 1755.
29. (a) I. Fernández and G. Frenking, Chem.−Eur. J., 2006, 12, 3617; (b) G. Frenking, M. Hermann, D. M. Andrada and N. Holzmann, Chem. Soc. Rev., 2016, 45, 1129; (c) G. Frenking, R. Tonner, S. Klein, N. Takagi, T. Shimizu, A. Krapp, K. K. Pandey and P. Parameswaran, Chem. Soc. Rev., 2014, 43, 5106; (d) C. Mohapatra, S. Kundu, A. N. Paesch, R. Herbst-Irmer, D. Stalke, D. M. Andrada, G. Frenking and H. W. Roesky, J. Am. Chem. Soc., 2016, 138, 10429; (e) R. Tonner and G. Frenking, Chem.−Eur. J., 2008, 14, 3260; (f) D. M. Andrada and G. Frenking, Angew. Chem. Int. Ed., 2015, 54, 12319 ( Angew. Chem. , 2015 , 127 , 12494–12500 ).
30. (a) M. Mitoraj and A. Michalak, Organometallics, 2007, 26, 6576; (b) M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962.
31. (a) T. Kottke and D. Stalke, J. Appl. Crystallogr., 1993, 26, 615; (b) D. Stalke, Chem. Soc. Rev., 1998, 27, 171.
32. SAINT, Bruker-AXS, Madison, WI, USA, 2013.
33. L. Krause, R. Herbst-Irmer, G. M. Sheldrick and D. Stalke, J. Appl. Crystallogr., 2015, 48, 3.
34. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3.
35. G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3.
36. C. B. Hübschle, G. M. Sheldrick and B. Dittrich, J. Appl. Crystallogr., 2011, 44, 1281.
37. B. Niepötter, R. Herbst-Irmer and D. Stalke, J. Appl. Crystallogr., 2015, 48, 1485.
38. (a) R. Destro and F. Merati, Acta Crystallogr., Sect. B: Struct. Sci., 1995, 51, 559; (b) S. Deuerlein, D. Leusser, U. Flierler, H. Ott and D. Stalke, Organometallics, 2008, 27, 2306; (c) C. F. Matta, J. Hernández-Trujillo, T.-H. Tang and R. F. W. Bader, Chem.−Eur. J., 2003, 9, 1940; (d) A. Haaland, D. J. Shorokhov and N. V. Tverdova, Chem.−Eur. J., 2004, 10, 4416; (e) L. J. Farrugia, C. Evans and M. Tegel, J. Phys. Chem. A, 2006, 110, 7952; (f) L. J. Farrugia, C. Evans, D. Lentz and M. Roemer, J. Am. Chem. Soc., 2009, 131, 1251.
39. H. Ott, U. Pieper, D. Leusser, U. Flierler, J. Henn and D. Stalke, Angew. Chem. Int. Ed., 2009, 48, 2978 ( Angew. Chem. , 2009 , 121 , 3022–3026 ).
40. E. A. Zhurova, V. V. Zhurov and A. A. Pinkerton, J. Am. Chem. Soc., 2007, 129, 13887.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental charge density investigation and computational details. CCDC 1590024–1590026. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7sc05368a

---