Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
How to tame a palladium terminal oxo†
Dominik
Munz
 *
*
Friedrich-Alexander Universität Erlangen-Nürnberg, Egerlandstr. 1, 91058 Erlangen, Germany. E-mail: dominik.munz@fau.de
First published on 13th December 2017
Abstract
The isolation of terminal oxo complexes of the late transition metals promises new avenues in oxidation catalysis like the selective and catalytic hydroxylation of unreactive CH bonds, the activation of water, or the upgrading of olefins. While terminal oxo ligands are ubiquitous for early transition metals, well-characterized examples with group 10 metals remain hitherto elusive. In search for palladium terminal oxo complexes, the relative stability/reactivity of such compounds are evaluated computationally (CASSCF/NEVPT2; DFT). The calculations investigate only well-known ligand systems with established synthetic procedures and relevance for coordination chemistry and homogeneous catalysis. They delineate and quantify, which electronic properties of ancillary ligands are crucial for taming otherwise highly reactive terminal oxo intermediates. Notably, carbene ligands with both strong σ-donor and strong π-acceptor properties are best suited for the stabilization of palladium(II) terminal oxo complexes, whereas ligands with a weaker ligand field lead to highly reactive complexes. Strongly donating ligands are an excellent choice for high-valent palladium(IV) terminal oxo compounds. Low coordinate palladium(II) as well as high-valent palladium(IV) complexes are best suited for the activation of strong bonds.
Introduction
Oxo compounds of the late transition metals are alleged intermediates in fundamental chemical processes like the refinement of small molecules through redox catalysis. Prominent examples are the platinum catalyzed oxidation of ammonia to nitric acid by O2 (Ostwald process) or CO/NOx emission control in the catalytic converters of automobiles by palladium (rhodium, platinum) catalysis.1,2 Group 10 terminal oxo compounds (i.e., M(O) with M = Ni, Pd, Pt) hold therefore in analogy to the very rich CH oxidation chemistry of early transition metal oxo compounds great promise for selective CH activation or the splitting of water.3–15 The development of novel catalytic approaches in these areas is highly desirable in the context of green and sustainable oxidation catalysis.16–25 Collision experiments in the gas phase and computational studies established that naked oxides of the group 10 metals react even with methane to produce methanol.26–32 Importantly, these gas phase studies substantiate the intermediacy of terminal metal oxides both in heterogeneous as well as in homogeneous reaction media. | (1) |
Accordingly, it was already proposed in the early 90s that palladium(IV) terminal oxo compounds constitute intermediates of the oxy-insertion reaction of alkanes with peroxides in the liquid phase.33–37 High-valent nickel(III)38–42 and platinum(IV)43 (or surrogates, respectively)44–46 terminal oxo species were equally suggested as intermediates for hydrocarbon functionalization chemistry.44–46 It is well known that the isolation of such compounds is very challenging due to the population of anti-bonding molecular orbitals (“oxo wall” for C4v symmetry).47–51 The synthesis, characterization and study of room temperature stable group 10 terminal oxo compounds remains consequently elusive.2,38,52–55 Nevertheless, Milstein and coworkers reported one surprising example, where a supposedly platinum(IV) terminal oxo complex was stabilized by an NCP pincer ligand. Whereas the high reactivity of the complex prevented characterization by X-ray crystallography, its oxygen transfer chemistry with carbon monoxide, phosphines, and dihydrogen could be evidenced.56
Even more surprisingly than the stability of the complex was the fact that the NCP pincer ligand did not feature strong π-backbonding capabilities.57 Up to this report, it was common believe that π-accepting ligands in a trigonal coordination environment should stabilize such compounds by releasing d-electron density from the transition metal center, thereby reducing the electron repulsion between the metal d-electrons and the p-electrons of the oxo ligand.57,58
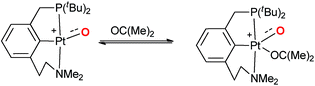 | (2) |
Later on, it was argued on the basis of computational investigations that both the excitation of d-electron density to s- and p-orbitals as well as the coordination of acetone in solution could stabilize this particular complex by supporting out of plane bending of the oxo ligand.59 We conclude therefore that the electronic factors leading to highly reactive or comparably stable group 10 terminal oxo compounds are only poorly understood.
Herein, the influence of ancillary ligands on the electronic properties and thermodynamic stability of palladium complexes with terminal oxido ligands is elucidated computationally.57 Provided that enough thermodynamic stability can be achieved, sterically encumbering ligands should be able to kinetically protect these reactive species, i.e. increase the barrier for O atom transfer.60–62 Eventually, the isolation and study of a stable terminal oxo compounds will then open up new avenues towards rational catalyst design for various applications.
Results and discussion
First, high-level quantum chemical calculations on the NEVPT2/CASSCF(8,8) level of theory will be used to reliably model the electronic properties of palladium terminal oxo complexes. Based on these results, a computationally more efficient approach using density functional theory (DFT) is applied. A series of palladium(II) and palladium(IV) complexes with different monodentate ancillary ligands (amines, pyridines, phosphines, isocyanides, series of carbenes) will be investigated with the latter method. We will show that the thermodynamic stability as well as electronic properties of such palladium(II) terminal oxo complexes can be qualitatively rationalized through σ-donor/π-acceptor effects of the ancillary ligand. The calculation of the related singlet/triplet gap of the complexes (PdII) allows for a quantification of the reactivity of the terminal oxo moiety. Contrarily, we will show that the π-acceptor effects are not important for the PdIV complexes, where the overall donor properties of the ancillary ligands determine the thermodynamic stability. Next, these results will be extended to chelating bidentate ligands and tricoordinate pincer-type ligands. Finally, overall trends in reactivity and electronic structure will be identified and implications for synthetic approaches will be discussed.63Computational methods
All singlet and triplet geometry optimizations were performed with Gaussian09, Rev. D01 (ref. 64) at the B3LYP-D3(BJ)/def2-TZVP65–68 (valence triple-ζ plus single polarization basis set)69 level of theory using the def2 quasirelativistic effective core potential (ECP, 28 core electrons) and the related def2-TZVP valence basis set for palladium as obtained from the emsl basis set exchange data base,69,70 and applying the D3 dispersion correction71 with Becke–Johnson damping.72 The restricted formalism was used for closed-shell singlet multiplicities. No symmetry or internal coordinate constraints were applied during optimizations. All reported optimized structures were verified as true minima by the absence of negative eigenvalues in the harmonic vibrational frequency analysis and all wave functions were checked for undesired internal instabilities. The energies of all structures were corrected by single-point calculations with ORCA (version 3.0.3) on the B2PLYP(COSMO, D3BJ)/def2-TZVPP level of theory, including corrections for solvent effects (except the structures shown in Table 1) with the conductor like screening model COSMO73 (solvent: hexane). The RIJCOSX approximation was used to speed up the calculations. Test calculations revealed negligible deviation from calculations without the RIJCOSX procedure. Tighter than default scf convergence criteria (tightscf), and finer than default grids (grid5; finalgrid6) were used as implemented in ORCA. Structures optimized with B3LYP and B2PLYP showed very similar structural parameters. The chosen computational method was benchmarked for the influence of functional (B3LYP, PBE0, M06, M06L, B2PLYP, B2GP-BLYP, PWP-B95), basis set [def2-SVP, def2-TZVP, def2-TZVPP, 6-31G(d), 6-311G(d,p), 6-311++G(d,p)] and dispersion and solvent corrections on experimental and computational results (structural parameters, multiplicities, energies) with Milstein's PtIV complex56,59 and Cundari's CASSCF(8,8) study44 on truncated PdIV bisimine complexes. For details, see the ESI.† Importantly, B3LYP, PBE0, M06 and M06L provided similar optimized structural parameters and consistent energy profiles, whereas it was found that triple-ζ basis sets are much better suited for the geometry optimizations than double-ζ basis sets. For energies of conformational and stereoisomers, see the ESI† as well. Structural optimizations using the complete active space SCF (CASSCF) method were performed with ORCA 3.0.3. Finer than default grid setting were chosen for the RIJCOSX approximation (IntAccX 4.34, 4.34, 4.67; GridX 2,2,2). The selection of the active space is delineated in more detail in the ESI.† The def2-ECP and related def2-TZVPP valence basis set was used as implemented in ORCA for Pd in conjunction with the def2-TZVPP all-electron basis set for the other elements. Effects of dynamic electron correlation were included by the second order multireference perturbation method NEVPT2.74 The optimized CASSCF structures were verified as true minima through numerical calculation of the hessian. The DLPNO-CCSD(T) calculations (“NORMAL” settings) were performed accordingly on the DLPNO-CCSD(T)/def2-TZVPP//B3LYP/def2-TZVP level of theory using ORCA 4.0.1. All energies reported – except in Table 1, which shows electronic energies – are Gibbs free energies under standard conditions (T = 298 K, p = 1 atm) using unscaled frequencies. Approximate Gibbs free energies were obtained through thermochemical analysis of the B3LYP-D3(BJ)/def2-TZVP optimized structures, using the thermal corrections to the Gibbs free energy as reported by Gaussian09 (including zero-point effects, thermal enthalpy corrections, and entropy) and the electronic energy including solvent effects and dispersion corrections from the single point calculations with ORCA. For a comparison to ΔE values, which reflect the same trends, see the ESI.† The biradical open-shell singlet electronic states were obtained through the broken-symmetry formalism via the flip-spin procedure of ORCA with the optimized triplet structures. Spin-decontamination through the Yamaguchi formula75–77 did not have a considerable influence on the obtained energy differences. The nature of the open-shell biradical wave functions was verified using corresponding orbitals and spin populations.78 Natural Bond Orbitals (NBOs) were calculated with NBO 6.0.79 The energy decomposition analysis (EDA) and analysis of fragment molecular orbitals was performed with AOMix v6.88 based on wave functions computed with Gaussian09 on the B2PLYP(D3BJ)/def2-TZVPP//B3LYP-D3/def2-TZVP level of theory.80,81 The EDA decomposes the overall bonding interaction energy (Eint) in orbital (Eorb: charge transfer and polarization effects) and steric contributions (Esteric: electrostatic and Pauli exchange energy). The Tolman electronic parameter of the CAAC, MIC, and DAC ligands were calculated according to Gusev's procedure with Gaussian09, rev. D01.82,83 Calculated structures, molecular orbitals and spin densities were visualized with IboView,84 Molden 5.6,85 and Avogadro 1.2.0.86| a CASSCF(8,8)/NEVPT2/def2-TZVPP. b B2PLYP/def2-TZVPP//B3LYP-D3/def2-TZVP. c DLPNO-CCSD(T)/def2-TZVPP//B3LYP/def2-TZVP. | |||
|---|---|---|---|
| ΔE CASSCF(8,8)/def2-SVP | +2.0 | 0 | +6.3 |
| ΔE CASSCF(8,8)/def2-TZVPP | +3.1 | +2.3 | 0 |
| ΔE CASSCF(8,8)/NEVPT2a | +1.6 | +4.9 | 0 |
| ΔE B2PLYP/def2-TZVPP | +1.6 | +6.9 | 0 |
| ΔE B2PLYP//B3LYPb | +1.8 | +9.6 | 0 |
| ΔE B3LYP/def2-TZVPP | −13.8 | n.d. | 0 |
| ΔE DLPNO-CCSD(T)//B3LYPc | 0 | n.d. | +4.7 |
Multireference character and perturbation theory results
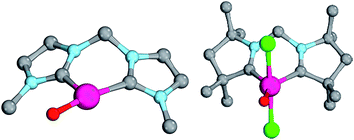
Computational modeling of late transition metal terminal oxo compounds is a challenge for single-determinantal DFT.87 In order to investigate the multireference character of a model PdIV oxo complex with a truncated bisimine ligand (ethane-1,2-dimine), a CASSCF(8,8) study using the 6-31+G(d,p) basis set was reported.44 The calculations, which included the π-system of the imine ligand as well as the σ- and one π-bond of the oxo ligand with the metal, suggested surprisingly that the molecule should have an open-shell singlet ground state. Indeed, we obtained even for the larger ligand with N-methyl substituents (N1,N2-dimethyl ethane-1,2-dimine) as well an open-shell singlet ground state using the def2-SVP basis set (Table 1; ΔEs/t = +2.0 kcal mol−1). However, when using a larger basis set (def2-TZVPP), the closed-shell singlet state becomes the ground state, whereas the triplet (CASSCF(8,8): ΔEs/t = +3.1 kcal mol−1) and open-shell singlet states (CASSCF(8,8): ΔEo.s.s. = +2.3 kcal mol−1) get less favorable.88The calculations are likewise in favor of a closed-shell singlet ground state, if dynamic correlation effects are considered via the n-electron valence state perturbation theory NEVPT2 correction74 on top of the converged CASSCF(8,8) wave function (CASSCF(8,8)/NEVPT2: ΔEs/t = +1.6 kcal mol−1; ΔEo.s.s. = +4.9 kcal mol−1). We consequently believe that an open-shell singlet ground state is quite unlikely, which is also indicated by state averaged CASSCF calculations (ESI†). The closed-shell singlet state shows a slightly distorted trigonal planar coordination geometry (Fig. 1). The occupation numbers (ON) of the Pd![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonding σ-orbital (1.9) and Pd
O bonding σ-orbital (1.9) and Pd![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonding π-orbital (ON: 1.8) indicate moderate population of the respective σ*- (ON: 0.1) and π*- (ON: 0.2) anti-bonding orbitals and consequently strong double bond character with an overall PdO bond order between one and two.
O bonding π-orbital (ON: 1.8) indicate moderate population of the respective σ*- (ON: 0.1) and π*- (ON: 0.2) anti-bonding orbitals and consequently strong double bond character with an overall PdO bond order between one and two.
It was reported for Milstein's platinum(IV) complex that the double-hybrid functional B2GP-BLYP predicted the experimentally observed singlet multiplicity much better than the hybrid functional PBE0, which is known to be biased towards the high-spin state.59,89 Indeed, although the optimized structural parameters are very similar to the CASSCF(8,8) results, also B3LYP predicts a fairly large singlet/triplet gap of ΔEs/t = −13.8 kcal mol−1 in favor of the triplet state (Table 1). Additionally, it appears interesting to note that single-reference coupled cluster calculations on the DLPNO-CCSD(T) level of theory predict a triplet ground state as well (ΔEs/t = −4.7 kcal mol−1).90 Contrarily, the CASSCF(8,8)/NEVPT2 results could be perfectly reproduced on the computationally demanding B2PLYP/def2-TZVPP level of theory (ΔEs/t = +1.6 kcal mol−1). Geometry optimization with the open-shell singlet biradical wavefunction91,92 predicted in agreement with the NEVPT2 results (ΔEo.s.s. = +4.9 kcal mol−1) the open-shell singlet state (ΔEo.s.s. = +6.9 kcal mol−1) to be higher in energy than the high-spin triplet state (ΔEo.s.s. = +1.8 kcal mol−1). Fortunately, the singlet–triplet gap could as well be described well by single-point calculations on the B2PLYP/def2-TZVPP//B3LYP/def2-TZVP level of theory (ΔEs/t = +1.8 kcal mol−1). For the determination of the open-shell singlet energy, the very similar geometrical parameters of the triplet state and the flip-spin procedure as implemented in ORCA was used. Here, the stability of the open-shell singlet state was a bit underestimated supposedly due to the unrelaxed open-shell singlet structure (ΔEo.s.s. = +9.6 kcal mol−1).
Altogether, both DFT and CASSCF give coherent results and confirm that closed-shell singlet and triplet state energies are close in energy, with a closed-shell singlet ground state. Notably, also single-point calculations on the B2PLYP//B3LYP level of theory give reliable singlet/triplet gap energies. Therefore, all the following results refer to the latter level of theory. For further benchmarking studies relating to the choice of functional, basis set, and influence of dispersion and solvation effects, see the ESI (Fig. S1, Tables S1 and S2†).
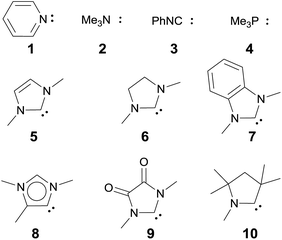
We anticipated that carbene ligands97–99 qualify as ideal candidates for two reasons. First, they are (unlike phosphines) typically stable under oxidative conditions. Second, there is a large variety of electronically distinct free carbenes beyond the very well-known imidazole-2-ylidenes (NHC, 5) available for the convenient synthesis of transition metal carbene complexes. Examples range from dihydroimidazole-2-ylidenes (saNHC, 6) and benzimidazolylidenes (benzNHC, 7) to mesoionic carbenes (MICs, 8),100,101 diamidocarbenes (DACs, 9)102 and cyclic (alkyl)(amino) carbenes (CAACs, 10).103,104 A popular method for the description of the donor properties of ligands is the Tolman electronic parameter (TEP). The TEP, which is obtained through determination of the CO stretching frequencies of (L)Ni(CO)3 complexes, is related to the overall donor properties of a ligand and combines both σ- and π-effects as well as steric contributions.105,106 According to the TEP, mesoionic carbene ligands (8), which do not show considerable π-accepting properties, are exceptionally strong donor ligands. The electron deficient diamidocarbene 9 is expected by the TEP to be a very weak donor ligand. In extension, the 13C and 15N NMR shifts of the free carbenes,10731P and 77Se of phosphinidene and selenium adducts,108–110 and DFT calculations111–117 allowed for deconvolution of both σ-donor and π-acceptor effects.
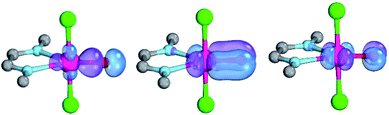
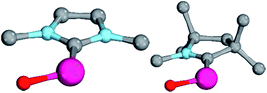
Magnetic circular dichroism studies allowed to evaluate the influence of NHC ligands on the ligand field of iron(II) complexes.118,119 It has been reported that an ordering of both carbene ligands and N-donor as well as P-donor ligands according to their ligand field is a challenging task due to side effects with the ancillary ligands.119 Nevertheless, it can be argued that CAAC (10) ligands with their very strong σ-donor and π-acceptor capabilities should be extraordinary strong field ligands. Consequently, benzNHCs (7, fairly strong σ-donor, fairly weak π-acceptor), NHCs (5, strong σ-donor, weak π-acceptor), and especially N-donor (1, 2) and P-donor ligands (4) should lead to smaller ligand field splittings. Optimizing the structures of the LPdIIO complexes with these monodentate ligands L (B2PLYP(COSMO,D3)/def2-TZVPP//B3LYP/def2-TZVP) reveals that the singlet states are lower in energy than the triplet states for all the investigated carbene ligands (vide infra). Strongly bent coordination geometries with short distances between the oxo moiety and the N-methyl substituents of the carbene ligands (Fig. 2; 5PdO: CH3–O 2.00 Å; 10PdO: CH3–O 2.01 Å) are predicted for all singlet state structures, whereas pseudo-linear structures were optimized for the open-shell states (ESI†). The linear coordination geometry represents however a transition state for the closed-shell molecules. The complex with an NHC ligand (5PdO) shows a C–Pd–O angle of 107.7° and the CAAC complex (10PdO) of 110.9° (Fig. 2). The short distances between the oxo atom and the N-methyl substituents indicate weak hydrogen type bonding, which further stabilizes the terminal oxo group through delocalization of electron density.120,121 Note that it has been shown that hydrogen bonding interactions can be crucial for the stabilization of terminal oxo groups.122 Most importantly, the computed Pd–O bond length is predicted to be significantly shortened with 1.79 Å (5PdO: 1.80 Å) in comparison with crystallographically characterized Pd–O single bonds, which are typically around 2.06 Å.44
The shorter bond between the CAAC ligand and the palladium atom (1.93 Å) for 10PdO in comparison to the NHC complex 5PdO (1.97 Å) is indicative of stronger interaction between the metal atom and the carbene ligand (Fig. 3). The Mayer bond indices for the Pd–O bond indicate considerable multiple bond character (5PdO: 1.47; 10PdO: 1.53) and are in good agreement with the natural atomic orbital Wiberg bond index for oxygen (5PdO: 1.40; 10PdO: 1.46). Natural resonance theory123 predicts as well a considerable double bond character (ESI, Fig. S4†), although the resonance weights for a double bond description are comparably small with 24% for a Pd![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O double bond for 5PdO and 23% for 10PdO, respectively.
O double bond for 5PdO and 23% for 10PdO, respectively.
Complementing the partial double bond character of the Pd–O bond, considerable negative partial charge is localized on the terminal oxo atom (5PdO: Löwdin: −0.48 a.u.; Hirshfeld: −0.60 a.u., NPA: −0.94 a.u.; 10PdO: Löwdin: −0.50 a.u.; Hirshfeld: −0.62 a.u.; NPA: −0.95 a.u.). Also note the higher accumulation of positive charge on the palladium atom for L = CAAC vs. L = NHC, which suggests enhanced relieve of d-electron density for 10PdO.
(CAAC: Löwdin +0.14 a.u.; Hirshfeld: +0.35 a.u.; NPA: +0.64 a.u.; 5PdO: Löwdin: +0.12 a.u.; Hirshfeld: +0.33 a.u.; NPA: +0.62 a.u.). The computational results suggest hence a fairly strong electrostatic interaction between the palladium and oxygen atoms. The bond properties of the oxygen – palladium bonds were furthermore investigated by Morokuma's energy decomposition analysis (EDA), which decomposes the overall bonding interaction (Eint) in orbital (Eorb) and steric contributions (Esteric).124–126 Indeed, the Pd–O bond (Table 2) of 10PdO was found to be stronger (Eint = −100.0 kcal mol−1) than the one of the NHC complex 5PdO (Eint = −97.2 kcal mol−1), which vice versa suggests higher reactivity (i.e. lability of the Pd–O bond) for the latter. Notably and in agreement with the analysis of the double bond character and geometrical parameters, this is mainly due to more favorable orbital interactions (Eorb = −230.0 kcal mol−1) for the CAAC complex 10PdO in comparison to the NHC analogue 5PdO (Eorb = −222.3 kcal mol−1).
| Fragments | Complex | E int | E orb | E steric |
|---|---|---|---|---|
| (CAAC)Pd–O | 10PdO | −100.0 | −230.0 | +130.0 |
| (NHC)Pd–O | 5PdO | −97.2 | −222.3 | +125.1 |
The bonding interaction between the carbene ligands and the palladium monoxide molecular fragment in the closed-shell singlet state ([1Σ+(π*4)])32 was as well investigated by energy decomposition (ESI, Table S3†). This approach corresponds to the picture of an “ancillary ligand stabilized palladium monoxide”. The decomposition analysis suggests also for this covalent bond a stronger interaction between the CAAC and PdO (Eint = −65.8 kcal mol−1) than for the NHC complex (Eint = −59.6 kcal mol−1).
The analysis of the Löwdin orbital population and the molecular orbital interaction diagram for 10PdO (ESI, Fig. S2†; fragments: PdO and the CAAC ligand) favor an overall Pd–O bond order between one and two, with the occupation of two π* antibonding orbitals of the Pd–O bond. Moderate (≈1 a.u.) excitation of 4d-electron density to the 5s and 5p orbitals is predicted. The bent coordination geometry of the oxo ligand optimizes the bonding and antibonding interactions between the oxo p- and metal d-orbitals through mixing of the d-orbitals.39
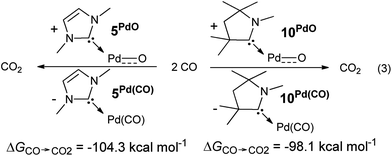
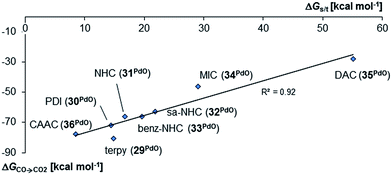
The oxygen atom transfer to carbon monoxide (i.e. the oxidation of carbon monoxide to carbon dioxide) by the CAAC complex 10PdO proceeds highly exergonic (10PdO: ΔGCO→CO2 = −98.1 kcal mol−1, Scheme 1) and therefore confirms that the complex is indeed a strong oxidant with strong O-atom transfer capability.
Interestingly, the oxygen atom transfer from the NHC complex 5PdO proceeds even more exergonic (5PdO: ΔGCO→CO2 = −104.3 kcal mol−1). This is in perfect agreement with the analysis of the molecular orbital interactions and indicates that 5PdO is more reactive than 10PdO. Markedly, the reduced exergonicity for the oxidation of CO by 10PdO relative to the oxidation by 5PdO is also in line with the shorter Pd–O bond length (vide supra, 5PdO, 1.80 Å; 10PdO, 1.79 Å), which should be related with the palladium–oxo bond strength (Badger's rule) and the oxophilicity38 of the (carbene)Pd fragment.
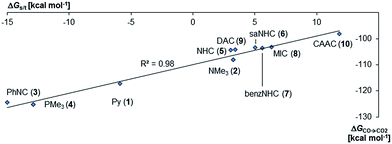
Next, the Gibbs free energy for the oxidation of CO to CO2 (ΔGCO→CO2) was studied as well for all the other ligands shown in Chart 1. Remarkably, the very strong field CAAC ligand led to the least exergonic oxidation reaction (ΔGCO→CO2 = −98.1 kcal mol−1), i.e. the CAAC stabilizes the terminal oxo ligand the most (Fig. 3). The ΔG values for ligands with a supposedly weaker ligand field like pyridine 1 (ΔGCO→CO2 = −117.3 kcal mol−1), the isonitrile ligand 3 (ΔGCO→CO2 = −123.3 kcal mol−1) or the phosphine PMe34 (ΔGCO→CO2 = −123.3 kcal mol−1) indicate thermodynamically much less stable terminal oxo complexes. The dihydroimidazolylidene (saNHC, 6) and benzimidazolylidene (benz-NHC, 7) ligands with their moderate π-accepting properties were predicted – in perfect agreement with the expectations – to be between the imidazolylidene (NHC, 5) and the CAAC ligand (10).
Next, a general method, which quantifies the ancillary ligand effects and therefore allows for the prediction of the thermodynamic stability of terminal oxo complexes, was sought. We anticipated that the singlet/triplet gap of terminal oxo compounds should be related to the stability of the complexes, because the excitation of the singlet into the triplet state is associated with transition from partial Pd![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O multiple bond character to a single bond (vide supra).
O multiple bond character to a single bond (vide supra).
Looking into the literature corroborates as well that thermodynamic considerations or respectively the singlet/triplet gap of a transition metal oxo complex could be a good indicator for its reactivity. It has been experimentally shown that the rate as well as the thermodynamics of CH activation by FeIV terminal oxo complexes with bispidine ligands are mainly dependent on the energy required for the spin-state crossover from S = 1 to S = 2.128 It was also proposed for iron(IV) model complexes that weak field ligands should lead to higher reaction rates for the activation of CH bonds.129,130 Equally, it was shown computationally for late transition metal amido and alkoxo compounds that ground state effects (i.e. the stability of the metal starting material) can be more important for CH activation reactivity than transition state effects.131,132 Schwarz concluded that the spin state and more precisely spin density on terminal oxyl moieties is important for an efficient hydrogen atom abstraction from hydrocarbons in the gas phase.133 Calculations by Ziegler suggested that thermodynamics as well as the HOMO–LUMO gap are important for the CH and OH activation reactivity of a chosen set of group 5–8 terminal oxo complexes.134
Indeed, the TEP, HOMO/LUMO energy levels of the ligands or partial charges of the coordinating carbene ligands (Pd, O atoms) are not very good indicators (ESI; Fig. S5–S7†) for the thermodynamic stability of the terminal oxo ligand. Contrarily, the ΔG value for the oxidation of carbon monoxide to carbon dioxide (ΔGCO→CO2) is related with the singlet/triplet gap (ΔGs/t) of the LPdO complexes (Fig. 3).135 Supposedly weaker field ligands stabilize the triplet over the singlet state (e.g., 3PdO: ΔGs/t = −15.0 kcal mol−1) and lead therefore to more reactive terminal oxo species. Strong field ligands like N-heterocyclic carbenes (5PdO: ΔGs/t = +3.0 kcal mol−1) and especially the CAAC ligand (10PdO ΔGs/t = +11.8 kcal mol−1) stabilize the singlet state and accordingly the terminal oxo ligand. The open-shell singlet states (o.s.s.) are predicted to not be energetically competitive with the closed-shell singlet state for most strong field ligands (ΔGs/o.s.s. > 10 kcal mol−1), but could become important for some of the weaker field ligands with a triplet ground state (ΔGs/o.s.s. < 10 kcal mol−1 for 1, 3, 4; ESI, Table S5†).
When looking at the corresponding PdIV complexes with two chlorido ligands, the triplet state becomes more stable than the closed-shell singlet state for all investigated ligands. The geometry optimizations reveal that the chlorido ligands are positioned perpendicular to the carbene pz orbital, thereby minimizing interaction between the potentially π-acidic carbene ligand and the transition metal (Fig. 4).
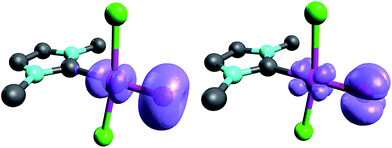 | ||
| Fig. 4 Structural parameters (C–Pd–O 180.0°, Pd–O 1.84 Å, Pd–C 2.03 Å) and spin density of NHC complex 5PdCl2O in the triplet state (left side) and open-shell singlet state (right side). | ||
In addition, the elongation of the carbene palladium bond to 2.03 Å suggests negligible π-backbonding from the transition metal to the carbene ligand. Accordingly, the NHC complex 5PdCl2O features a pseudo square planar coordination geometry with a still short Pd–O bond (1.84 Å), but a Mayer bond index of only 0.9 (Fig. 4, left side). The two unpaired electrons are localized on the oxygen and palladium atom, respectively, with only very few delocalization onto the carbene atom. This picture is complemented by the calculated partial charges on the palladium and oxygen atoms, respectively, which indicate less zwitterionic character as was predicted for the corresponding palladium(II) complexes (Löwdin partial charges for 5PdCl2O: O, +0.12 a.u.; Pd, −0.32 a.u.). The open-shell singlet state, which was calculated using the broken-symmetry formalism, is considerably higher in energy (ΔGt/o.s.s. = 9.8 kcal mol−1) and shows a similar spin density map like the triplet ground state (Fig. 4, right side). The reactivity of the palladium(IV) oxo complex 5PdCl2O is of course higher (ΔGCO→CO2 = −113.7 kcal mol−1) than the palladium(II) oxo complex 5PdO (ΔGCO→CO2 = −104.3 kcal mol−1).
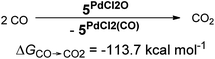 | (4) |
The overall oxidation strength of the palladium(IV) complexes with the carbene ligands seems to be correlated with the overall donor strength of the carbene ligand as obtained by the Tolman electronic parameter (ESI, Fig. S8†). However, the influence is small with ΔΔGCO→CO2 < 4 kcal mol−1 (3PdCl2O: −115.4 kcal mol−1; 8PdCl2O: −112.1 kcal mol−1) for all carbene ligands. Note the analogy with chromium(V) nitrido complexes with weak ancillary ligands, where it has been shown that the molecular orbital energies are dominated by the {CrN}2+ unit.136,137
Indeed, we observed the very same trends and behavior for the bidentate ligands. Again, the molecules are expected to have a singlet ground state e.g., a ΔGs/t of more 32 kcal mol−1 was predicted for the CAAC complex 24 (Fig. 5). The singlet diradical electronic state was confirmed to not be important for all carbene ligands (ESI, Table S7†). The calculations predict as well a correlation between ΔGs/t and ΔGCO→CO2. Importantly, the CAAC complexes (23PdO, 24PdO) are the most stable species, whereas the other carbene ligands and especially the N-donor ligands lead to much higher reactivity. Looking at the molecular structures of the complexes reveals in most cases similar structural parameters as were found for the monodentate ligands (Fig. 6, left side). The calculations predict T-shaped coordination geometries with a weak interaction between the N-methyl substituents and the terminal oxo ligand (1.94 Å). 24PdO and 23aPdO, which were optimized to a trigonal planar coordination geometry, are the most stable structures.
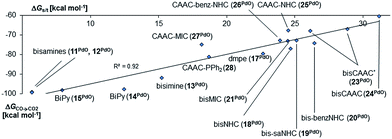 | ||
| Fig. 5 Correlation of singlet/triplet gap (ΔGs/t = Gtriplet − Gsinglet) of complexes with chelating ancillary ligands with Gibbs free energy for the oxidation of CO to CO2 (ΔGCO→CO2) by the complexes in the singlet state.140 | ||
All attempts to optimize trigonal planar coordination geometries for the other carbene ligands led to transition state structures, whereas optimizations of a T-shaped geometry for 24PdO evolved to be unstable. Notably, of the two diastereomers 23aPdO and 23bPdO, one was optimized to a T-shaped geometry, whereas the other one features a trigonal planar coordination geometry. Looking at the bond lengths of the Pd–O bond suggests slightly reduced double bond character for the bisNHC complex 18PdO (Pd–O: 1.83 Å) in relation to the bisCAAC complex 24PdO (Pd–O: 1.80 Å) or the complexes with monodentate ligands (5PdO: 1.80 Å; 10PdO: 1.79 Å; vide supra). The Mayer bond index predicts however the double bond character of the palladium oxygen bond to be slightly higher for the bidentate ligands (18PdO: 1.50; 24PdO: 1.63). The electrostatic interactions between the palladium atoms and oxo ligands (Löwdin partial charges for 18PdO: Pd, +/−0.00 a.u.; O, −0.64 a.u.; 24PdO: Pd, +0.06 a.u.; O, −0.63 a.u.) are larger for the bidentate than the monodentate ligands (5PdO: Pd, +0.12 a.u.; O: −0.48 a.u., vide supra). Looking at the Pd–O bond by energy decomposition analysis (Table 3) confirms a stronger bonding interaction for the trigonal planar bisCAAC complex 24PdO (Eint = −154.3 kcal mol−1) than for the T-shaped bisNHC complex (Eint = −140.2 kcal mol−1). Note that this time the steric repulsion energy (24PdO, Esteric = +61.8 kcal mol−1; 18PdO, Esteric = +114.3 kcal mol−1) is – contrarily to the monodentate complexes – much smaller for the bisCAAC complex 24PdO. Apparently the trigonal planar coordination geometry leads to combined reduced repulsive electrostatic and Pauli interactions, albeit at the cost of likewise reduced orbital stabilization (Eorb = −216.1 kcal mol−1). Looking at the isomeric bisCAAC complexes 23aPdO and 23bPdO supports this picture, with the trigonal planar coordination geometry showing much smaller steric repulsion energy (23aPdO, trigonal planar, Esteric = +78.5 kcal mol−1) than the T-shaped isomer (23bPdO, T-shaped, Esteric = +101.6 kcal mol−1). It was investigated, if the bidentate carbene ligands stabilize the palladium oxo species in the +IV oxidation state as well. The calculations predict the closed-shell singlet states to be more stable than the triplet states by at least ΔGs/t >8.5 kcal mol−1 for all carbene ligands; note that for amine, imine, and phosphine ligands smaller singlet/triplet gaps were obtained (vide supra; ESI, Table S8†). The open-shell singlet states for the complexes with carbene ligands are predicted to be in most cases considerably higher in energy than the closed-shell singlet states (ΔG > 12 kcal mol−1). All carbene complexes show trigonal-bipyramidal coordination geometries with the chlorido ligands in the apical positions (Fig. 7).
| E int | E orb | E steric | |
|---|---|---|---|
| 24PdO (L = bisCAAC; trigonal planar) | −154.3 | −216.1 | +61.8 |
| 23aPdO (L = bisCAAC, trigonal planar) | −146.7 | −225.2 | +78.5 |
| 23bPdO (L = bisCAAC, T-shaped) | −147.5 | −249.1 | +101.6 |
| 18PdO (L = bisNHC) | −140.2 | −254.5 | +114.3 |
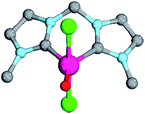 | ||
| Fig. 7 Structural parameters of 18PdCl2O in the singlet state. C–Pd–O 140.0°, Pd–O 1.79 Å, Pd–C 2.05 Å. | ||
As indicated by the Mayer bond indices and in agreement with the CASSCF(8,8) results for the bisimine ligand, the Pd–O bond shows still fairly strong double bond character (18PdCl2O: 1.40). Nevertheless, the zwitterionic character of the Pd–O bond is reduced through negative charge transfer from the chlorido ligands to the metal center (Löwdin partial charges for 18PdCl2O: Pd, −0.23; O, −0.41). In fact, the Pd–O bond is modeled to be of similar length like the singlet ground state monodentate palladium(II) complex 5PdCl2O (1.80 Å).
In agreement with the calculations on the triplet state of the mono coordinated palladium(IV) complexes, no correlation between ΔGs/t and of ΔGCO→CO2 could be found. However, the Tolman electronic parameter TEP seems to be fairly well correlated to the oxidation strength of the terminal oxo PdIV complex for the carbene ligands (Fig. 8). We conclude accordingly, that the stability of the singlet palladium(IV) terminal oxo complexes is rather dominated by the stabilization of the high-valent metal center, instead of orbital interactions with the oxo ligand. Notably, the Gibbs free enthalpy for the oxidation of the PdIICl2 complexes to the respective PdIVOCl2 compounds by dimethyl dioxirane (DMDO) ranges from −2 to +9 kcal mol−1 (ESI, Fig. S12†). This suggests that the experimental isolation of such a complex should be possible.
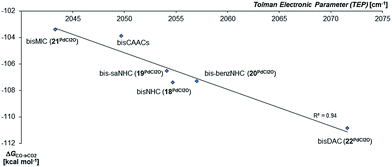 | ||
| Fig. 8 Correlation of the Gibbs free energy for the oxidation of CO to CO2 (ΔGCO→CO2) by the palladium(IV) complexes with bidentate carbene ligands in the singlet state with the Tolman Electronic Parameter TEP (donicity).141 The values of the bisCAAC complexes 23PdCl2O and 24PdCl2O are averaged. | ||
Enhanced electron donation from three L donor ligands in comparison to the bidentate coordination geometries leads to an elongation of the Pd–O bonds for the singlet-state palladium(II) complexes (Fig. 9; 31PdO: 1.86 Å) and a reduction of the Mayer bond order (1.21) in comparison to the bidentate ligand (vide supra). The charge separation within the Pd–O bond was found to be slightly larger (Löwdin partial charges for 31PdO: O, −0.68 a.u.; Pd, −0.02 a.u.). Again, weak hydrogen bonding type interactions were found between the N-methyl substituents and the terminal oxo ligand.
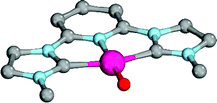 | ||
| Fig. 9 Structural parameters of 31PdO in the singlet ground state. C–Pd–O 101.6°, Pd–O 1.86 Å, Pd–C 2.01 Å. | ||
Surprisingly, the Gibbs free energy of the oxidation of CO to CO2 (ΔGCO→CO2) do not follow the same order as was obtained for the monodentate and bidentate cases. Whereas once more the stability of the palladium oxo compounds seems to be quite well correlated with the singlet/triplet gap of the complexes, the π-acidic CAAC ligand leads this time to a much more reactive compound than both the very electron rich mesoionic carbene (34PdO) or the very electron poor diamidocarbene (35PdO) ligand (Fig. 10).
Examination of the triplet state wave functions reveals that the electronic structures of all these compounds show strong delocalization of spin density from the metal onto the pincer ligand (Fig. 11, left side).144,145 Whereas both the monodentate NHC complex 5PdO (Fig. 4) and the bidentate complex 18PdO (Fig. 6, left side) show localization of most spin density on the metal center with some delocalization onto the carbene atom, the complex 31PdO involves a mainly pyridine centered radical with only few spin density on the metal atom (Fig. 11, left side). Therefore, simple donor–acceptor considerations are not an appropriate tool to explain reactivity trends. However, the relation shown in Fig. 10 strongly suggests that redox active ligands can be harnessed for the stabilization of terminal oxo complexes.
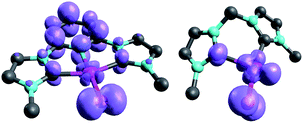 | ||
| Fig. 11 Spin densities of NHC complex 31PdO (left side) and 18PdO (right side) in the triplet states. | ||
Looking at the pincer ligands with palladium in the oxidation state of +IV reveals that the triplet multiplicity should be more stable than the singlet state, albeit by less than 10 kcal mol−1 (ESI, Table S11†). The open-shell singlet biradicals are expected to be only slightly higher in energy than the triplet biradicals and in the same order of magnitude like the closed-shell singlet states (roughly 10 kcal mol−1 higher than the triplet states; ESI, Table S11†). The influence of the specific pincer ligand on the oxidation of CO to CO2 (ΔGCO→CO2) seems to be less important than for the neutral palladium(IV) complexes with bidentate ligands (Fig. 12; e.g.30PdO+: ΔGCO→CO2 = −111.8 kcal mol−1; 34PdO+: ΔGCO→CO2 = −107.6 kcal mol−1).
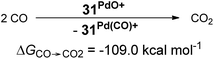 | (5) |
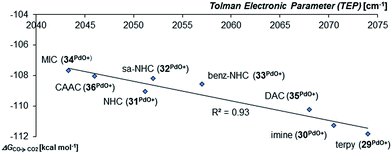 | ||
| Fig. 12 Correlation of the Tolman Electronic Parameter TEP (donicity) with Gibbs free energy for the oxidation of CO to CO2 (ΔGCO→CO2) by the cationic PdIV pincer complexes in the triplet state.48 | ||
Nevertheless, there seems to be again a tentative connection between the overall donicity of the ligands, i.e. the Tolman electronic parameter, and the thermodynamic stability of the palladium terminal oxo complexes (Fig. 12). The correlation is in fact surprisingly good, considering that the TEP includes steric contributions and that it has been noted that values from different families of ligands (C-donor, N-donor, P-donor) can usually not be compared.
Table 4 shows a summary of the most important trends for the different evaluated ligand systems and oxidation states. As can be seen, the stability of the palladium(II) complexes as well as the Pd–O bond length increases with the number of ancillary L type ligands. A closed shell singlet ground state was found for almost all complexes in the oxidation state of +II and the oxidation strength is correlated with the singlet/triplet gap of the terminal oxo complexes. For the palladium(IV) complexes, various electronic ground states (closed-shell singlet, open-shell singlet, triplet) are possible in dependence of the ancillary ligands. Notably, the oxidation strength of these complexes seems not to be dependent on the singlet/triplet gap of the particular complex, but rather the overall donor capabilities of ancillary ligands. Furthermore, an overall cationic charge as modeled with the L2X pincer ligands seems to enhance the reactivity of these complexes. We predict therefore that (transient) low-coordinate palladium(II) and high-valent palladium(IV) terminal oxo complexes are best suited for the activation of strong bonds like e.g. C–H bonds. However, whereas the ancillary ligands have a huge influence on the O-atom transfer capabilities of the palladium(II) complexes, they allow only for a fine tuning for the palladium(IV) compounds.
| Oxidation state | Ligand | Spin state | ΔGCO→CO2 [kcal mol−1] | Pd–O bond length [Å] | Descriptor |
|---|---|---|---|---|---|
| a Redox non-innocence of ligands in triplet state. b Influence small (ΔΔGCO→CO2 < 4 kcal mol−1). c Influence small (ΔΔGCO→CO2 < 5 kcal mol−1). | |||||
| +II | L | s | −104.3 | 1.80 | ΔGs/t |
| +II | L2 | s | −77.1 | 1.83 | ΔGs/t |
| +II | L3 | s | −66.2 | 1.86 | (ΔGs/t)a |
| +IV | L | t (o.s.s.) | −113.7 | 1.84 | (TEP)b |
| +IV | L2 | s (t, o.s.s.) | −106.5 | 1.79 | TEP |
| +IV | L2X+ | t (s, o.s.s) | −109.0 | 1.82 | (TEP)c |
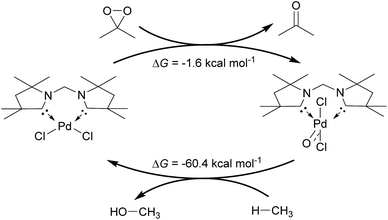
Inspired by the development of new catalytic processes for the activation of strong O–H and C–H bonds, we investigated briefly the thermodynamics for the catalytic oxidation of methane by the model complex 24PdCl2O (Fig. 13). The formation of the terminal oxo complex 24PdCl2O is predicted to be thermodynamically feasible through oxidation of the dichloride palladium(II) complex 24PdCl2 by dimethyldioxirane (DMDO; ΔG = −1.6 kcal mol−1). The oxyinsertion reaction with methane is very exergonic with ΔG = −60.4 kcal mol−1. We conclude therefore that O-atom transfer reactivity should be comparably facile for all complexes investigated herein. The oxidation step to generate the palladium terminal oxo compound appears to be potentially more challenging.
Conclusions
Palladium terminal oxo complexes in the oxidation state of +II are predicted to show significant multiple bond character and closed-shell singlet ground states. Both the σ-donating and π-accepting properties as perfectly exemplified by ancillary cyclic (alkyl)(amino)carbene (CAAC) ligands in comparison to conventional NHC ligands are important for their thermodynamic stability. The singlet/triplet gap of the complexes, which can be controlled by the electronic properties of the ancillary ligand, is proposed to determine the reactivity of the terminal oxo group. Accordingly, potential redox activity of ancillary ligands has a remarkable influence on the electronic structure and stability.Hydrogen bonds, which delocalize electron density from the terminal oxo ligand, enhance the stability of the basic terminal oxo complexes. Increasing the number of coordinating L-type ancillary ligands from one to three reduces the bond order, increases the dipolar character and reduces the reactivity of the Pd–O moiety. Overall, low-coordinate palladium(II) terminal oxo intermediates are therefore especially promising targets for the design of catalytic cycles for the activation of strong bonds.
The electronic structures of the complexes in the oxidation state of +IV are more diverse. Whereas for some cases the singlet state seems to be most stable (bidentate ligands), other ligand frameworks seem to rather favor the triplet configuration (monodentate ligands). Pd–O bonds with strong single-bond character are predicted. Most salient, the stability of the palladium(IV) complexes is shown to be related to the overall donor properties of the ancillary ligands, although the influence is especially for the molecules with a triplet ground state small. The stability of these complexes can be quantified by the Tolman Electronic Parameter of the ancillary ligand. On the contrary to the palladium(II) complexes, the π-accepting properties of ancillary ligands are not very important. Consequently, strongly donating ligands are best suited for synthetic endeavors towards the isolation of high valent palladium(IV) terminal oxo compounds. Accordingly, it also appears very plausible why Milstein's platinum(IV) terminal oxo complex did not feature a ligand with considerable π-acceptor capabilities. Of particular interest, palladium(IV) terminal oxos appear to be generally quite reactive and suitable candidates for the activation of very strong bonds.
In sight of those predictions, we believe that the synthetic isolation of palladium terminal oxo compounds is feasible with ancillary ligand systems providing balanced electronic stabilization and kinetic protection through a sterically encumbering ligand system. Consequently, we hope that such exciting compounds will become available for the scientific community in the future and will allow for the development of novel catalytic oxidation protocols.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Thanks are due to the German Academic Exchange Service DAAD for a postdoctoral fellowship and the Fonds der Chemischen Industrie im Verband der Chemischen Industrie e.V. for a Liebig fellowship. The W. M. Keck Foundation (“Keck2”; UC San Diego) and the Regionales Rechenzentrum Erlangen RRZE (“Woodcrest”; FAU Erlangen) are acknowledged for computational resources. Prof. K. Meyer and Prof. G. Bertrand are acknowledged for their generous support; PD Dr M. Khusniyarov and Prof. D. J. Mindiola are thanked for helpful discussions.Notes and references
- M. Shelef, Chem. Rev., 1995, 95, 209–225 CrossRef CAS.
- P. R. Sharp, J. Chem. Soc., Dalton Trans., 2000, 2647–2657 RSC.
- J. Hohenberger, K. Ray and K. Meyer, Nat. Commun., 2012, 3, 720 CrossRef PubMed.
- B. Meunier, S. P. de Visser and S. Shaik, Chem. Rev., 2004, 104, 3947–3980 CrossRef CAS PubMed.
- B. Meunier and J. Bernadou, in Metal-Oxo and Metal-Peroxo Species in Catalytic Oxidations, ed. B. Meunier, Springer Berlin Heidelberg, Berlin, Heidelberg, 2000, pp. 1–35 Search PubMed.
- L. Que and W. B. Tolman, Nature, 2008, 455, 333–340 CrossRef CAS PubMed.
- S. A. Cook, D. C. Lacy and A. S. Borovik, in Spin States in Biochemistry and Inorganic Chemistry, John Wiley & Sons, Ltd, 2015, pp. 203–227 Search PubMed.
- R. H. Holm, Chem. Rev., 1987, 87, 1401–1449 CrossRef CAS.
- M. Zhou and R. H. Crabtree, Chem. Soc. Rev., 2011, 40, 1875–1884 RSC.
- A. Gunay and K. H. Theopold, Chem. Rev., 2010, 110, 1060–1081 CrossRef CAS PubMed.
- D. Balcells, E. Clot and O. Eisenstein, Chem. Rev., 2010, 110, 749–823 CrossRef CAS PubMed.
- P. Du and R. Eisenberg, Energy Environ. Sci., 2012, 5, 6012–6021 CAS.
- S. Ye and F. Neese, Curr. Opin. Chem. Biol., 2009, 13, 89–98 CrossRef CAS PubMed.
- P. E. M. Siegbahn and R. H. Crabtree, in Metal-Oxo and Metal-Peroxo Species in Catalytic Oxidations, ed. B. Meunier, Springer Berlin Heidelberg, Berlin, Heidelberg, 2000, pp. 125–144 Search PubMed.
- For examples of the group 9, see (a) B. Wang, Y. M. Lee, W. Y. Tcho, S. Tussupbayev, S. T. Kim, Y. Kim, M. S. Seo, K. B. Cho, Y. Dede, B. C. Keegan, T. Ogura, S. H. Kim, T. Ohta, M. H. Baik, K. Ray, J. Shearer and W. Nam, Nat. Commun., 2017, 8, 14839 CrossRef CAS PubMed; (b) R. S. Hay-Motherwell, G. Wilkinson, B. Hussain-Bates and M. B. Hursthouse, Polyhedron, 1993, 12, 2009–2012 CrossRef CAS.
- A. E. Shilov and G. B. Shulpin, Chem. Rev., 1997, 97, 2879–2932 CrossRef CAS PubMed.
- E. G. Chepaikin, Russ. Chem. Rev., 2011, 80, 363–396 CrossRef CAS.
- K. I. Goldberg and A. S. Goldman, Activation and Functionalization of C-H Bonds, American Chemical Society, Washington, DC, 2004 Search PubMed.
- J. A. Labinger and J. E. Bercaw, Nature, 2002, 417, 507–514 CrossRef CAS PubMed.
- B. G. Hashiguchi, S. M. Bischof, M. M. Konnick and R. A. Periana, Acc. Chem. Res., 2012, 45, 885–898 CrossRef CAS PubMed.
- R. H. Crabtree, in Handbook of Green Chemistry – Green Catalysis: 1, ed. P. T. Anastas, Wiley-VCH, Weinheim, 2009 Search PubMed.
- Top. Organomet. Chem., Organometallic Oxidation Catalysis, ed. F. Meyer and C. Limberg, 2007, vol. 22, 2007 Search PubMed.
- H. Schwarz, Angew. Chem., Int. Ed., 2011, 50, 10096–10115 CrossRef CAS PubMed.
- A. N. Vedernikov, Acc. Chem. Res., 2012, 45, 803–813 CrossRef CAS PubMed.
- A. N. Campbell and S. S. Stahl, Acc. Chem. Res., 2012, 45, 851–863 CrossRef CAS PubMed.
- R. Wesendrup, D. Schröder and H. Schwarz, Angew. Chem., Int. Ed., 1994, 33, 1174–1176 CrossRef.
- A. Božović, S. Feil, G. K. Koyanagi, A. A. Viggiano, X. Zhang, M. Schlangen, H. Schwarz and D. K. Bohme, Chem.–Eur. J., 2010, 16, 11605–11610 CrossRef PubMed.
- J. Roithova and D. Schroder, Chem. Rev., 2010, 110, 1170–1211 CrossRef CAS PubMed.
- D. Schröder and H. Schwarz, Angew. Chem., Int. Ed., 1995, 107, 1973–1995 CrossRef.
- D.-Y. Hwang and A. M. Mebel, J. Phys. Chem. A, 2002, 106, 12072–12083 CrossRef CAS.
- E. Broclawik, R. Yamauchi, A. Endou, M. Kubo and A. Miyamoto, Int. J. Quantum Chem., 1997, 61, 673–682 CrossRef CAS.
- E. Broclawik, R. Yamauchi, A. Endou, M. Kubo and A. Miyamoto, J. Chem. Phys., 1996, 104, 4098–4104 CrossRef CAS.
- P. L. Alsters, H. T. Teunissen, J. Boersma, A. L. Spek and G. v. Koten, Organometallics, 1993, 12, 4691–4696 CrossRef CAS.
- A. Behnia, P. D. Boyle, J. M. Blacquiere and R. J. Puddephatt, Organometallics, 2016, 35, 2645–2654 CrossRef CAS.
- K. Kamaraj and D. Bandyopadhyay, Organometallics, 1999, 18, 438–446 CrossRef CAS.
- P. Wadhwani and D. Bandyopadhyay, Organometallics, 2000, 19, 4435–4436 CrossRef CAS.
- J. E. Kukowski, K. J. Keuseman and I. P. Smoliakova, Transition Met. Chem., 2015, 40, 877–889 CrossRef CAS.
- F. F. Pfaff, F. Heims, S. Kundu, S. Mebs and K. Ray, Chem. Commun., 2012, 48, 3730–3732 RSC.
- T. Corona, F. F. Pfaff, F. Acuña-Parés, A. Draksharapu, C. J. Whiteoak, V. Martin-Diaconescu, J. Lloret-Fillol, W. R. Browne, K. Ray and A. Company, Chem.–Eur. J., 2015, 21, 15029–15038 CrossRef CAS PubMed.
- T. Corona and A. Company, Chem.–Eur. J., 2016, 22, 13422–13429 CrossRef CAS PubMed.
- S. Yao and M. Driess, Acc. Chem. Res., 2012, 45, 276–287 CrossRef CAS PubMed.
- M. Sankaralingam, M. Balamurugan, M. Palaniandavar, P. Vadivelu and C. H. Suresh, Chem.–Eur. J., 2014, 20, 11346–11361 CrossRef CAS PubMed.
- K. R. Pellarin, M. S. McCready and R. J. Puddephatt, Organometallics, 2012, 31, 6388–6394 CrossRef CAS.
- T. M. Figg, G. Schoendorff, B. Chilukuri and T. R. Cundari, Organometallics, 2013, 32, 4993–4996 CrossRef CAS.
- T. M. Figg, J. R. Webb, T. R. Cundari and T. B. Gunnoe, J. Am. Chem. Soc., 2012, 134, 2332–2339 CrossRef CAS PubMed.
- T. M. Figg, T. R. Cundari and T. B. Gunnoe, Organometallics, 2011, 30, 3779–3785 CrossRef CAS.
- J. M. Mayer, Comments Inorg. Chem., 1988, 8, 125–135 CrossRef CAS.
- J. F. Berry, Comments Inorg. Chem., 2009, 30, 28–66 CrossRef CAS.
- J. R. Winkler and H. B. Gray, Struct. Bonding, 2012, 142, 17–28 CrossRef CAS.
- C. J. Ballhausen and H. B. Gray, Inorg. Chem., 1962, 1, 111–122 CrossRef CAS.
- T. A. Betley, Q. Wu, T. Van Voorhis and D. G. Nocera, Inorg. Chem., 2008, 47, 1849–1861 CrossRef CAS PubMed.
- K. Ray, F. Heims and F. F. Pfaff, Eur. J. Inorg. Chem., 2013, 2013, 3784–3807 CrossRef CAS.
- A. Singh, U. Anandhi, M. A. Cinellu and P. R. Sharp, Dalton Trans., 2008, 2314–2327 RSC.
- K. P. O'Halloran, C. C. Zhao, N. S. Ando, A. J. Schultz, T. F. Koetzle, P. M. B. Piccoli, B. Hedman, K. O. Hodgson, E. Bobyr, M. L. Kirk, S. Knottenbelt, E. C. Depperman, B. Stein, T. M. Anderson, R. Cao, Y. V. Geletii, K. I. Hardcastle, D. G. Musaev, W. A. Neiwert, X. K. Fang, K. Morokuma, S. X. Wu, P. Kogerler and C. L. Hill, Inorg. Chem., 2012, 51, 7025–7031 CrossRef PubMed.
- T. M. Anderson, W. A. Neiwert, M. L. Kirk, P. M. B. Piccoli, A. J. Schultz, T. F. Koetzle, D. G. Musaev, K. Morokuma, R. Cao and C. L. Hill, Science, 2012, 337, 290 CrossRef CAS PubMed.
- E. Poverenov, I. Efremenko, A. I. Frenkel, Y. Ben-David, L. J. W. Shimon, G. Leitus, L. Konstantinovski, J. M. L. Martin and D. Milstein, Nature, 2008, 455, 1093–1096 CrossRef CAS.
- C. Limberg, Angew. Chem., Int. Ed., 2009, 48, 2270–2273 CrossRef CAS PubMed.
- E. Spaltenstein, R. R. Conry, S. C. Critchlow and J. M. Mayer, J. Am. Chem. Soc., 1989, 111, 8741–8742 CrossRef CAS.
- I. Efremenko, E. Poverenov, J. M. L. Martin and D. Milstein, J. Am. Chem. Soc., 2010, 132, 14886–14900 CrossRef CAS PubMed.
- J. P. Wagner and P. R. Schreiner, Angew. Chem., Int. Ed., 2015, 54, 12274–12296 CrossRef CAS PubMed.
- J. P. Wagner and P. R. Schreiner, J. Chem. Theory Comput., 2016, 12, 231–237 CrossRef CAS PubMed.
- R. Okazaki, Heteroat. Chem., 2014, 25, 293–305 CrossRef CAS.
- K. J. Bonney and F. Schoenebeck, Chem. Soc. Rev., 2014, 43, 6609–6638 RSC.
- M. J. Frisch, et al., Gaussian 09, Rev. D01, Gaussian Inc.: Wallingford CT, 2009 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785–789 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- A. Klamt and G. Schueuermann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J. P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef CAS.
- N. Ferre, N. Guihery and J. P. Malrieu, Phys. Chem. Chem. Phys., 2015, 17, 14375–14382 RSC.
- S. Yamanaka, T. Kawakami, H. Nagao and K. Yamaguchi, Chem. Phys. Lett., 1994, 231, 25–33 CrossRef CAS.
- J. P. Malrieu and G. Trinquier, J. Phys. Chem. A, 2012, 116, 8226–8237 CrossRef CAS PubMed.
- F. Neese, J. Phys. Chem. Solids, 2004, 65, 781–785 CrossRef CAS.
- E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2013, 34, 1429–1437 CrossRef CAS PubMed.
- S. I. Gorelsky, AOMix: Program for Molecular Orbital Analysis, version 6.88, 2016, http://www.sg-chem.net Search PubMed.
- S. I. Gorelsky and A. B. P. Lever, J. Organomet. Chem., 2001, 635, 187–196 CrossRef CAS.
- D. G. Gusev, Organometallics, 2009, 28, 6458–6461 CrossRef CAS.
- D. G. Gusev, Organometallics, 2009, 28, 763–770 CrossRef CAS.
- G. Knizia and J. E. M. N. Klein, Angew. Chem., Int. Ed., 2015, 54, 5518–5522 CrossRef CAS PubMed.
- G. Schaftenaar and J. H. Noordik, J. Comput.-Aided Mol. Des., 2000, 14, 123–134 CrossRef CAS PubMed.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 1–17 Search PubMed.
- M. C. Lehman, D. R. Pahls, J. M. Meredith, R. D. Sommer, D. M. Heinekey, T. R. Cundari and E. A. Ison, J. Am. Chem. Soc., 2015, 137, 3574–3584 CrossRef CAS PubMed.
- Exploratory calculations with larger active spaces with the inclusion of further d-orbitals suggest as well a singlet ground state.
- M. Reiher, Inorg. Chem., 2002, 41, 6928–6935 CrossRef CAS PubMed.
- C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106 CrossRef PubMed.
- For examples with terminal manganese oxo compound, see (a) R. Gupta, T. Taguchi, B. Lassalle-Kaiser, E. L. Bominaar, J. Yano, M. P. Hendrich and A. S. Borovik, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 5319–5324 CrossRef CAS PubMed; (b) D. C. Ashley and M. Baik, ACS Catal., 2016, 6, 7202–7209 CrossRef CAS; (c) B. Lassalle-Kaiser, C. Hureau, D. A. Pantazis, Y. Pushkar, R. Guillot, V. K. Yachandra, J. Yano, F. Neese and E. Anxolabehere-Mallart, Energy Environ. Sci., 2010, 3, 924–938 RSC ; for an example involving a copper oxyl intermediate, see S. M. Huber, M. Z. Ertem, F. Aquilante, L. Gagliardi, W. B. Tolman and C. J. Cramer, Chem.–Eur. J., 2009, 15, 4886–4895 CrossRef CAS PubMed ; for examples regarding redox-active ligands, see (d) N. Muresan, C. C. Lu, M. Ghosh, J. C. Peters, M. Abe, L. M. Henling, T. Weyhermüller, E. Bill and K. Wieghardt, Inorg. Chem., 2008, 47, 4579–4590 CrossRef CAS PubMed; (e) V. Bachler, G. Olbrich, F. Neese and K. Wieghardt, Inorg. Chem., 2001, 41, 4179–4193 CrossRef ; for application of the broken symmetry formalism with redox active CAAC ligands, see ; (f) K. C. Mondal, B. Dittrich, B. Maity, D. Koley and H. W. Roesky, J. Am. Chem. Soc., 2014, 136, 9568–9571 CrossRef CAS PubMed; (g) A. P. Singh, P. P. Samuel, H. W. Roesky, M. C. Schwarzer, G. Frenking, N. S. Sidhu and B. Dittrich, J. Am. Chem. Soc., 2013, 135, 7324–7329 CrossRef CAS PubMed.
- J. Grafenstein, E. Kraka, M. Filatov and D. Cremer, Int. J. Mol. Sci., 2002, 3, 360–394 CrossRef.
- D. J. Mindiola, R. Waterman, V. M. Iluc, T. R. Cundari and G. L. Hillhouse, Inorg. Chem., 2014, 53, 13227–13238 CrossRef CAS PubMed.
- D. J. Mindiola and G. L. Hillhouse, J. Am. Chem. Soc., 2001, 123, 4623–4624 CrossRef CAS PubMed.
- N. D. Harrold and G. L. Hillhouse, Chem. Sci., 2013, 4, 4011–4015 RSC.
- R. Waterman and G. L. Hillhouse, J. Am. Chem. Soc., 2003, 125, 13350–13351 CrossRef CAS PubMed.
- F. E. Hahn and M. C. Jahnke, Angew. Chem., Int. Ed., 2008, 47, 3122–3172 CrossRef CAS PubMed.
- M. Melaimi, M. Soleilhavoup and G. Bertrand, Angew. Chem., Int. Ed., 2010, 49, 8810–8849 CrossRef CAS PubMed.
- S. P. E. Nolan, N-Heterocyclic Carbenes in Synthesis, Wiley-VCH, New-York, 2006 Search PubMed.
- R. H. Crabtree, Coord. Chem. Rev., 2013, 257, 755–766 CrossRef CAS.
- O. Schuster, L. R. Yang, H. G. Raubenheimer and M. Albrecht, Chem. Rev., 2009, 109, 3445–3478 CrossRef CAS PubMed.
- T. W. H. a. C. W. Bielawski, J. Am. Chem. Soc., 2009, 131, 16039–16041 CrossRef PubMed.
- M. Soleilhavoup and G. Bertrand, Acc. Chem. Res., 2015, 48, 256–266 CrossRef CAS PubMed.
- S. Roy, K. C. Mondal and H. W. Roesky, Acc. Chem. Res., 2016, 49, 357–369 CrossRef CAS PubMed.
- D. J. Nelson and S. P. Nolan, Chem. Soc. Rev., 2013, 42, 6723–6753 RSC.
- T. Droge and F. Glorius, Angew. Chem., Int. Ed., 2010, 49, 6940–6952 CrossRef PubMed.
- K. C. Mondal, S. Roy, B. Maity, D. Koley and H. W. Roesky, Inorg. Chem., 2016, 55, 163–169 CrossRef CAS PubMed.
- O. Back, M. Henry-Ellinger, C. D. Martin, D. Martin and G. Bertrand, Angew. Chem., Int. Ed., 2013, 52, 2939–2943 CrossRef CAS PubMed.
- A. Liske, K. Verlinden, H. Buhl, K. Schaper and C. Ganter, Organometallics, 2013, 32, 5269–5272 CrossRef CAS.
- S. V. C. Vummaleti, D. J. Nelson, A. Poater, A. Gomez-Suarez, D. B. Cordes, A. M. Z. Slawin, S. P. Nolan and L. Cavallo, Chem. Sci., 2015, 6, 1895–1904 RSC.
- D. M. Andrada, N. Holzmann, T. Hamadi and G. Frenking, Beilstein J. Org. Chem., 2015, 11, 2727–2736 CrossRef CAS PubMed.
- D. Nemcsok, K. Wichmann and G. Frenking, Organometallics, 2004, 23, 3640–3646 CrossRef CAS.
- R. Tonner, G. Heydenrych and G. Frenking, Chem.–Asian J., 2007, 2, 1555–1567 CrossRef CAS PubMed.
- H. Jacobsen, A. Correa, A. Poater, C. Costabile and L. Cavallo, Coord. Chem. Rev., 2009, 253, 687–703 CrossRef CAS.
- H. Jacobsen, A. Correa, C. Costabile and L. Cavallo, J. Organomet. Chem., 2006, 691, 4350–4358 CrossRef CAS.
- T. Strassner, Top. Organomet. Chem., in Metal Carbenes in Organic Synthesis, ed. K. H. Dötz, 2004, vol. 13 Search PubMed.
- H. V. Huynh and G. Frison, J. Org. Chem., 2013, 78, 328–338 CrossRef CAS PubMed.
- T. M. Baker, T. L. Mako, A. Vasilopoulos, B. Li, J. A. Byers and M. L. Neidig, Organometallics, 2016, 35, 3692–3700 CrossRef CAS.
- K. L. Fillman, J. A. Przyojski, M. H. Al-Afyouni, Z. J. Tonzetich and M. L. Neidig, Chem. Sci., 2015, 6, 1178–1188 RSC.
- S. J. K. Jensen, T.-H. Tang and I. G. Csizmadia, J. Phys. Chem. A, 2003, 8975–8979 CrossRef CAS.
- S. J. Grabowski, Chem. Rev., 2011, 111, 2597–2625 CrossRef CAS PubMed.
- C. E. MacBeth, R. Gupta, K. R. Mitchell-Koch, V. G. Young, G. H. Lushington, W. H. Thompson, M. P. Hendrich and A. S. Borovik, J. Am. Chem. Soc., 2004, 126, 2556–2567 CrossRef CAS PubMed.
- E. D. Glendening and F. Weinhold, J. Comput. Chem., 1998, 19, 593–609 CrossRef CAS.
- K. Kitaura and K. Morokuma, Int. J. Quantum Chem., 1976, 10, 325–340 CrossRef CAS.
- T. Ziegler and A. Rauk, Theor. Chim. Acta, 1977, 46, 1–10 CrossRef CAS.
- M. v. Hopffgarten and G. Frenking, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 43–62 CrossRef.
- The basis set superposition error (BSSE) was estimated via counterpoise calculation to be +4.1 kcal mol−1, whereas the D3 dispersion correction leads to a stabilization of −3.0 kcal mol−1.
- P. Comba, S. Fukuzumi, C. Koke, B. Martin, A.-M. Löhr and J. Straub, Angew. Chem., Int. Ed., 2016, 55, 11129–11133 CrossRef CAS PubMed.
- A. Kazaryan and E. J. Baerends, ACS Catal., 2015, 5, 1475–1488 CrossRef CAS.
- S. Ye, C.-Y. Geng, S. Shaik and F. Neese, Phys. Chem. Chem. Phys., 2013, 15, 8017–8030 RSC.
- D. H. Ess, T. B. Gunnoe, T. R. Cundari, W. A. Goddard and R. A. Periana, Organometallics, 2010, 29, 6801–6815 CrossRef CAS.
- D. Devarajan, T. B. Gunnoe and D. H. Ess, Inorg. Chem., 2012, 51, 6710–6718 CrossRef CAS PubMed.
- N. Dietl, M. Schlangen and H. Schwarz, Angew. Chem., Int. Ed., 2012, 51, 5544–5555 CrossRef CAS PubMed.
- L. Q. Deng and T. Ziegler, Organometallics, 1996, 15, 3011–3021 CrossRef CAS.
- D. N. Bowman, A. Bondarev, S. Mukherjee and E. Jakubikova, Inorg. Chem., 2015, 54, 8786–8793 CrossRef CAS PubMed.
- T. Birk and J. Bendix, Inorg. Chem., 2003, 42, 7608–7615 CrossRef CAS PubMed.
- J. Bendix, J. Am. Chem. Soc., 2003, 125, 13348–13349 CrossRef CAS PubMed.
- J. Chu, D. Munz, R. Jazzar, M. Melaimi and G. Bertrand, J. Am. Chem. Soc., 2016, 138, 7884–7887 CrossRef CAS PubMed.
- J. A. Mata, M. Poyatos and E. Peris, Coord. Chem. Rev., 2007, 251, 841–859 CrossRef CAS.
- 16PdO and 22PdO are omitted due to instability towards the formation of phosphine oxide (16PdO) or instability of the carbonyl Pd0 complex (22PdO).
- TEP values were obtained from ref. 82 (NHC, sa-NHC, benz-NHC) or calculated accordingly (MIC, CAAC, DAC). For further details see the ESI.†.
- M. Poyatos, J. A. Mata and E. Peris, Chem. Rev., 2009, 109, 3677–3707 CrossRef CAS PubMed.
- S. C. Bart, K. Chłopek, E. Bill, M. W. Bouwkamp, E. Lobkovsky, F. Neese, K. Wieghardt and P. J. Chirik, J. Am. Chem. Soc., 2006, 128, 13901–13912 CrossRef CAS PubMed.
- V. Lyaskovskyy and B. de Bruin, ACS Catal., 2012, 2, 270–279 CrossRef CAS.
- L. A. Berben, B. de Bruin and A. F. Heyduk, Chem. Commun., 2015, 51, 1553–1554 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Atomic coordinates, energies (ΔE, ΔG), detailed benchmark tests (basis set, functional, corrections for dispersion and solvent effects), molecular orbital diagrams for 5PdO and 10PdO, natural resonance theory results, details of CASSCF calculations, energies of isomers, other (non)linear correlations, calculation of TEP values and complete ref. 64. See DOI: 10.1039/c7sc05034h |
| This journal is © The Royal Society of Chemistry 2018 |