Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Impact of ambient gases on the mechanism of [Cs8Nb6O19]-promoted nerve-agent decomposition†‡
Alexey L.
Kaledin
a,
Darren M.
Driscoll
 b,
Diego
Troya
b,
Daniel L.
Collins-Wildman
c,
Craig L.
Hill
b,
Diego
Troya
b,
Daniel L.
Collins-Wildman
c,
Craig L.
Hill
 *c,
John R.
Morris
*b and
Djamaladdin G.
Musaev
*c,
John R.
Morris
*b and
Djamaladdin G.
Musaev
 *ab
*ab
aC. L. Emerson Center for Scientific Computation and Department of Chemistry, Emory University, Atlanta, Georgia 30322, USA. E-mail: dmusaev@emory.edu
bDepartment of Chemistry, Virginia Tech, Blacksburg, Virginia, 24061, USA. E-mail: jmorris@vt.edu
cDepartment of Chemistry, Emory University, Atlanta, Georgia 30322, USA. E-mail: chill@emory.edu
First published on 8th January 2018
Abstract
The impact of ambient gas molecules (X), NO2, CO2 and SO2 on the structure, stability and decontamination activity of Cs8Nb6O19 polyoxometalate was studied computationally and experimentally. It was found that Cs8Nb6O19 absorbs these molecules more strongly than it adsorbs water and Sarin (GB) and that these interactions hinder nerve agent decontamination. The impacts of diamagnetic CO2 and SO2 molecules on polyoxoniobate Cs8Nb6O19 were fundamentally different from that of NO2 radical. At ambient temperatures, weak coordination of the first NO2 radical to Cs8Nb6O19 conferred partial radical character on the polyoxoniobate and promoted stronger coordination of the second NO2 adsorbent to form a stable diamagnetic Cs8Nb6O19/(NO2)2 species. Moreover, at low temperatures, NO2 radicals formed stable dinitrogen tetraoxide (N2O4) that weakly interacted with Cs8Nb6O19. It was found that both in the absence and presence of ambient gas molecules, GB decontamination by the Cs8Nb6O19 species proceeds via general base hydrolysis involving: (a) the adsorption of water and the nerve agent on Cs8Nb6O19/(X), (b) concerted hydrolysis of a water molecule on a basic oxygen atom of the polyoxoniobate and nucleophilic addition of the nascent OH group to the phosphorus center of Sarin, and (c) rapid reorganization of the formed pentacoordinated-phosphorus intermediate, followed by dissociation of either HF or isopropanol and formation of POM-bound isopropyl methyl phosphonic acid (i-MPA) or methyl phosphonofluoridic acid (MPFA), respectively. The presence of the ambient gas molecules increases the energy of the intermediate stationary points relative to the asymptote of the reactants and slightly increases the hydrolysis barrier. These changes closely correlate with the Cs8Nb6O19–X complexation energy. The most energetically stable intermediates of the GB hydrolysis and decontamination reaction were found to be Cs8Nb6O19/X-MPFA-(i-POH) and Cs8Nb6O19/X-(i-MPA)-HF both in the absence and presence of ambient gas molecules. The high stability of these intermediates is due to, in part, the strong hydrogen bonding between the adsorbates and the protonated [Cs8Nb6O19/X/H]+-core. Desorption of HF or/and (i-POH) and regeneration of the catalyst required deprotonation of the [Cs8Nb6O19/X/H]+-core and protonation of the phosphonic acids i-MPA and MPFA. This catalyst regeneration is shown to be a highly endothermic process, which is the rate-limiting step of the GB hydrolysis and decontamination reaction both in the absence and presence of ambient gas molecules.
Introduction
The design of materials that can rapidly, fully, and catalytically decontaminate chemical warfare agents (CWAs) and other toxic compounds is an increasingly active area of research and one that presents some questions in fundamental chemistry.1–5 As suggested by enzymatic chemistry, some of the most effective strategies for CWA destruction involve catalyzed hydrolysis reactions.4 Specifically, it is well established that the P–X bonds (X = F, CN, SR, etc.) of organophosphorus (OP) nerve agents rapidly inactivate acetylcholinesterase (a serine hydrolase), the enzyme that facilitates hydrolysis of the neurotransmitter acetylcholine in the nervous system. This inactivation occurs through rapid nucleophilic addition and irreversible binding of the serine OH to the phosphorus atom of the nerve agent. Thus, an atomistic/molecular level understanding of the hydrolysis of OP compounds by nucleophilic addition and other processes may lead to the development of more effective materials and catalysts for nerve agent decontamination. Ongoing research efforts have identified several organic and inorganic materials, including metal–organic frameworks (MOFs, especially UiO-66, NU-1000 and MOF-808),5–10 polyoxometalates (POMs),11–14 MOF/POM hybrid materials,15,16 zirconium hydroxide,17 zeolites,18 and organic polymers,19 as effective OP hydrolysis materials.Recently, the use of POMs to catalyze nerve agent decontamination has attracted wide attention, in part because POMs are molecular representations of metal oxides and are thus far more amenable than the latter to extensive synthetic compositional alteration and characterization at the molecular level.20,21 Polyoxoniobates (PONbs), including [Nb6O19]8−, are effective OP nerve agent hydrolysis compounds because their high negative charge densities (negative charge per polyanion oxygen) render them highly basic and nucleophilic. Thus, it is not surprising that the synthesis and in-depth analysis of the structures and reactivities of various (alkali and organic) salts of PONbs continue to be the focus of extensive studies.22,23 These studies show that the structures and, consequently, the catalytic activities of these materials for nerve agent decontamination depend on many factors, including (but not limited to) the nature of the counter-cation, the pH of the solution, the aggregate state (powder or solid-state material) of the catalyst, the real-time environmental conditions, and the nature and concentration of ambient gas molecules.
Earlier research on Lindqvist hexaniobate alkali salts (M8Nb6O19, M = Li, K, Cs) reported rapid hydrolysis of the OP agent Sarin (GB, propan-2-yl methylphosphonofluoridate, see Scheme 1) both in aqueous solution and at the gas–surface interface.11 Small-angle X-ray scattering (SAXS) measurements showed aggregation of the OP compounds on the polyoxoniobate (PONb), which led to the suggestion that the reaction follows a general base hydrolysis mechanism.12 Our subsequent computational study on the mechanism of decomposition of GB by a Cs-salt of PONb, Cs8Nb6O19 (or CsPONb), confirmed the general base hydrolysis mechanism of this reaction at the gas–surface interface.24
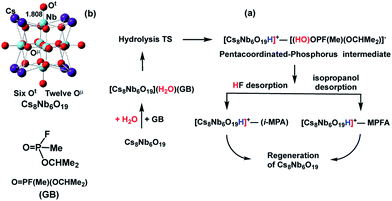 | ||
| Scheme 1 Schematics of: (a) the mechanism of Sarin (GB) hydrolysis (reported in ref. 24) promoted by the Cs8Nb6O19 polyoxoniobate and (b) the Cs8Nb6O19 polyoxoniobate. | ||
Briefly, we have found that GB degradation by Cs8Nb6O19 includes the following elementary steps (see Scheme 1): (a) the adsorption of water and the nerve agent on the Cs8Nb6O19 species, (b) concerted dissociation of the adsorbed water molecule on a basic oxygen atom of the polyoxoniobate and nucleophilic addition of the nascent OH group to the phosphorus center of the nerve agent, (c) rapid reorganization of the resulting pentacoordinated phosphorus intermediate by dissociation of either HF or isopropanol, and formation of POM-bound isopropyl methyl phosphonic acid (i-MPA) or methyl phosphonofluoridic acid (MPFA), respectively. The calculations showed that the phosphonic acids i-MPA and MPFA are strongly bound to the protonated [Cs8Nb6O19H]+-core through hydrogen bonds and electrostatic interactions with the Cs counter-ions, suggesting that full catalyst regeneration may require additional treatment and depends on the nature of the counter-cations as well as the real-time (ambient) experimental conditions.
Although PONb catalysts have been shown to react with CWAs, the chemistry has yet to be characterized in the presence of ambient gases (for example, NO2, CO2 and SO2), which may affect the stabilities, structural motifs, and activities of the PONb catalysts. Because this issue is vital to the application of PONbs as decontamination catalysts in real conditions, this paper probes the impact of the common battlefield contaminants NO2, CO2 and SO2 on the structure, stability and decontamination activity of the exemplary PONb species Cs8Nb6O19. This study addresses in depth the effects of these ambient gases on the structures of the catalysts and the base hydrolysis mechanism for Sarin degradation using density functional theory (DFT) calculations and infrared (IR) spectroscopy.
Results and discussion
A. Structure of Cs8Nb6O19 in the presence of gaseous CO2, NO2 and SO2
Here, we divide our discussion into two subsections. First, we discuss the interaction of diamagnetic CO2 and SO2 molecules with Cs8Nb6O19; then, we present our findings on the interactions between NO2 radical and Cs8Nb6O19.| ΔE | ΔH | ΔG | |
|---|---|---|---|
| Ot: Cs8Nb6O19 + CO2 | −29.1 | −29.0 | −23.2 |
| Oμ: Cs8Nb6O19 + CO2 | −16.8 | −16.7 | −10.8 |
| Ot: Cs8Nb6O19 + SO2 | −48.2 | −47.6 | −40.3 |
| Oμ: Cs8Nb6O19 + SO2 | −34.7 | −34.1 | −26.6 |
| CsN: Cs8Nb6O19 + NO2 | −21.7 | −22.2 | −22.1 |
| Ot: Cs8Nb6O19 + NO2 | −18.8 | −18.7 | −13.9 |
| CsN and Ot: Cs8Nb6O19 + 2NO2 | −77.4 | −74.6 | −58.0 |
| Cs8Nb6O19/CO2(Ot) + H2O | −24.2 | −22.4 | −11.9 |
| Cs8Nb6O19/SO2(Ot) + H2O | −22.7 | −21.0 | −9.7 |
| Cs8Nb6O19 + H2O | −24.6 | −23.6 | −17.3 |
| Cs8Nb6O19/H2O + GB | −18.8 | −17.4 | −4.2 |
| Cs8Nb6O19/H2O/CO2(Ot) + GB | −18.0 | −17.4 | −2.4 |
| Cs8Nb6O19/H2O/SO2(Ot) + GB | −17.4 | −16.4 | −3.7 |
The factors that impact the strength of the Cs8Nb6O19/X bonding and site-preference of absorption were analyzed by investigating the resulting geometries of these complexes. From Fig. 1, where we present the most important geometries of the Cs8Nb6O19/X(Ot) and Cs8Nb6O19/X(Oμ) isomeric species for X = CO2 and SO2 (for full geometries of these species, see the ESI‡), we make the following conclusions:
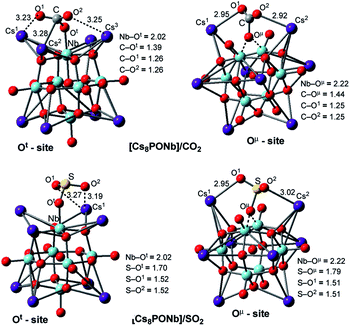 | ||
| Fig. 1 Adsorption of the ambient gas molecules CO2 and SO2 on Cs8Nb6O19 at the Ot sites (left) and bridging sites (right) with their important geometry parameters (in Å). | ||
(a) The CO2 molecule in Cs8Nb6O19/CO2(Ot) is bound to Cs8Nb6O19via multiple interactions, including two (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)CO2⋯Cs interactions and one C–Ot interaction. The long calculated bond distances for the Cs–O1, Cs–O2 and Cs–C interactions (3.23, 3.25 and 3.28 Å, respectively) indicate they are relatively weak. In contrast, the C–Ot interaction is stronger, with a bond distance of 1.39 Å. As a result of this strong interaction, the Nb–Ot distance is elongated from 1.80 Å to 2.02 Å (see Fig. 1). Thus, while the interactions with the Cs cations provide additional stability to the complex Cs8Nb6O19/CO2(Ot), the primary interaction occurs between the C atom of CO2 and the terminal oxygen atom of Cs8Nb6O19.
O)CO2⋯Cs interactions and one C–Ot interaction. The long calculated bond distances for the Cs–O1, Cs–O2 and Cs–C interactions (3.23, 3.25 and 3.28 Å, respectively) indicate they are relatively weak. In contrast, the C–Ot interaction is stronger, with a bond distance of 1.39 Å. As a result of this strong interaction, the Nb–Ot distance is elongated from 1.80 Å to 2.02 Å (see Fig. 1). Thus, while the interactions with the Cs cations provide additional stability to the complex Cs8Nb6O19/CO2(Ot), the primary interaction occurs between the C atom of CO2 and the terminal oxygen atom of Cs8Nb6O19.
In the Cs8Nb6O19/CO2(Oμ) isomer, where CO2 interacts with a bridging oxygen, the C–Oμ bond distance is longer (calculated to be 1.44 Å) than the C–Ot bond distance in Cs8Nb6O19/CO2(Ot), while the Cs–O1 and Cs–O2 interactions are slightly stronger (based on the calculated Cs–O1 and Cs–O2 distances). The above presented geometry parameters of Cs8Nb6O19/CO2(Ot) and Cs8PONb/CO2(Oμ) not only explain the calculated energy difference between these species, but are also consistent with the amounts of charge transfer from Cs8Nb6O19 to CO2: in the Cs8Nb6O19/CO2(Ot) and Cs8Nb6O19/CO2(Oμ) complexes, almost 0.8 |e| and 0.4 |e| negative charge is transferred from Cs8Nb6O19 to CO2, respectively. Furthermore, the putative CO3-group in Cs8Nb6O19/CO2(Ot) has a total negative charge of 1.52 |e|.
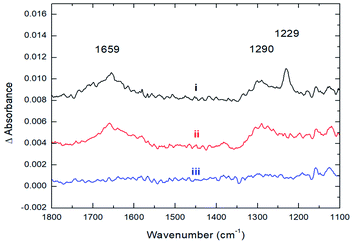
The strong coordination of CO2 to Cs8Nb6O19 is also supported by IR spectroscopic studies, where the adsorption of CO2 onto Cs8Nb6O19 was investigated by recording the infrared spectra before, during, and after exposure of Cs8Nb6O19 to a constant flux of CO2. Upon adsorption of CO2 on Cs8Nb6O19, three prominent features appeared in the infrared spectrum (Fig. 2, i) at 1659 cm−1, 1290 cm−1 and 1229 cm−1. Interestingly, we observed no feature in the infrared spectrum around 2300 cm−1, which would be associated with a linear CO2 molecule bound to the POM surface. The 1229 cm−1 and 1290 cm−1 bands are consistent with the IR-inactive symmetric stretch from the gas-phase (ν1(C–O)), which becomes IR active upon binding to the POM. The 1659 cm−1 band is likely related to the antisymmetric ν3(C–O) stretch of CO2/CO3 (occurs at 2349 cm−1 in the gas-phase25 and significantly redshifts upon adsorption). The presence of both the ν1 and ν3 bands in the infrared spectrum indicates a bent structure of the adsorbate at the surface. Upon evacuation of CO2 from the chamber, the 1229 cm−1 spectroscopic feature diminishes, indicating that this band corresponds to the vibrational motion of weakly bound CO2 species on the surface (Fig. 2, ii); however, the two other features (1659 and 1290 cm−1) persist until annealing the Cs8Nb6O19 sample at 423 K (Fig. 2, iii). The elevated temperature required to fully remove the CO2 suggests that the molecules responsible for these infrared bands are strongly bound to Cs8Nb6O19. The experimentally observed IR features are in full agreement with the DFT calculations (harmonic, un-scaled). Indeed, the two prominent IR active features at 1290 and 1659 cm−1, which are ascribed to the bending and asymmetric CO stretch motions of a bent CO2 molecule, are calculated to be 1316 and 1317 cm−1 (for the bend) and 1702 and 1719 cm−1 (for the asymmetric stretch) in Cs8Nb6O19/CO2(Ot) and Cs8Nb6O19/CO2(Oμ), respectively. Thus, the above presented experimental and computational analysis shows that a large fraction of the adsorbed CO2 strongly binds to Cs8Nb6O19. Once at the surface, the molecule adopts a bent geometry, which activates the ν1 vibrational motion toward absorption of infrared radiation.
(b) The geometric features of Cs8Nb6O19/SO2(Ot) and Cs8Nb6O19/SO2(Oμ) adducts are similar to those of their CO2 analogs: among the interactions, the strongest are the S–Ot and S–Oμ interactions, with 1.70 and 1.79 Å bond distances, respectively. These geometry parameters are consistent with the greater stability of the Cs8Nb6O19/SO2(Ot) isomer. Furthermore, comparison of the calculated Cs8Nb6O19–X binding energies shows that SO2 interacts with Cs8Nb6O19 much more strongly, by nearly a factor of two, than CO2. However, both molecules clearly persist on the POM at ambient and well above ambient temperatures.
Further calculations showed that single Cs8Nb6O19 species can bind several CO2 and SO2 molecules. As seen in Table 2, where we have summarized the adsorption energies as a function of the number of molecules adsorbed at the six Ot sites, there is a pronounced monotonic convergence of the electronic and enthalpy binding energies up to n = 6. The free energies, on the other hand, reveal thermodynamic instability for CO2 adsorption at larger values of n, suggesting that only the Cs8Nb6O19/(CO2)n species with n ≤ 4 are viable. The Cs8Nb6O19/(SO2)n species may still be stable for n > 6.
| n | X = CO2 | X = SO2 | ||||
|---|---|---|---|---|---|---|
| Z = E | Z = H | Z = G | Z = E | Z = H | Z = G | |
| 1 | −29.1 | −29.0 | −23.2 | −48.2 | −47.6 | −40.3 |
| 2 | −22.9 | −21.8 | −11.2 | −43.3 | −42.4 | −27.6 |
| 3 | −19.6 | −18.9 | −9.6 | −38.8 | −37.1 | −27.3 |
| 4 | −13.3 | −12.5 | −0.7 | −34.2 | −32.9 | −19.8 |
| 5 | −7.3 | −6.6 | 4.4 | −26.9 | −25.9 | −14.9 |
| 6 | −2.2 | −2.0 | 6.9 | −29.0 | −27.9 | −16.9 |
The calculations show that N2O4 is planar, with an N–N bond distance of 1.85 Å, which is significantly longer than the average N–N single bond length of 1.45 Å; this species has a dimerization energy of ΔE/ΔH/ΔG = 19.8/17.3/5.6 kcal mol−1. Unlike NO2, N2O4 is diamagnetic and coordinates to the Cs8Nb6O19 catalyst (see Fig. 3) with a Cs8Nb6O19–N2O4 interaction energy of ΔE/ΔH/ΔG = −25.3/−25.3/−18.5 kcal mol−1. Secondly, as shown in Table 1 and Fig. 3, the “free” NO2 radical (at ambient temperature) can interact with polyoxoniobate to form the [Cs8Nb6O19]/NO2 adduct. This adduct exists in two energetically stable isomeric forms, Cs8Nb6O19/NO2(Ot) and Cs8Nb6O19/NO2(CsN); the most favorable form is Cs8Nb6O19/NO2(CsN), where the N atom of NO2 interacts with two Cs centers (with Cs1–N and Cs2–N distances of 3.42 and 3.44 Å). To our surprise, these Cs–N interactions lead to electron transfer from Cs8Nb6O19 to NO2 in Cs8Nb6O19/NO2(CsN), as evidenced by population analysis: the calculated Mulliken spin/charge is NO2(CsN) = 0.34/−0.65 |e|. Thus, as a result of these interactions, almost 0.65 |e| charge is transferred from Cs8Nb6O19 to NO2; and, consequently, the Cs8Nb6O19 unit develops partial radical character. Further analysis shows that most of the unpaired spin of Cs8Nb6O19 is located on the internal OIN-center (∼0.24 |e|) and the bridging Oμ (∼0.14 |e|) located close to the Cs atoms coordinated to NO2, while the remaining spin is delocalized on all other atoms of the polyoxoniobate. Similarly, but to a lesser extent, NO2(Ot) has a 0.67/−0.41 |e| spin/charge distribution in the Cs8Nb6O19/NO2(Ot) isomer. The calculated Cs8Nb6O19–NO2 binding energies are ΔH/ΔG = −22.2/−22.1 and −18.7/−13.9 kcal mol−1 in Cs8Nb6O19/NO2(CsN) and Cs8Nb6O19/NO2(Ot), respectively.
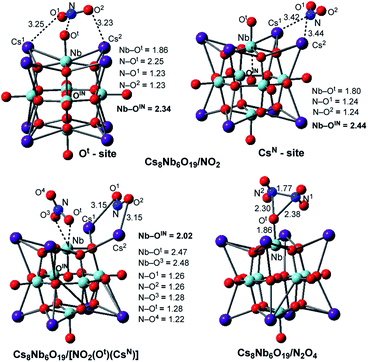 | ||
| Fig. 3 The calculated most energetically stable structures of NO2 and N2O4 adsorbed on Cs8Nb6O19, with their important geometry parameters (in Å). | ||
Consequently, the acquired partial radical character of Cs8Nb6O19 in the Cs8Nb6O19/NO2(CsN) complex significantly increases its NO2-affinity, enabling strong coordination of another (second) NO2 radical to the Ot-site of polyoxoniobate and formation of the most thermodynamically favorable Cs8Nb6O19/[NO2(CsN)NO2(Ot)] singlet species. The calculated energy of the reaction Cs8Nb6O19/NO2(CsN) + NO2 → Cs8Nb6O19/[NO2(CsN)NO2(Ot)] is ΔE/ΔH/ΔG = −55.8/−52.4/−35.9 kcal mol−1, while the energy of the Cs8Nb6O19/NO2(Ot) + NO2 → Cs8Nb6O19/[NO2(CsN)NO2(Ot)] reaction is ΔE/ΔH/ΔG = −63.8/−61.5/−52.8 kcal mol−1 (see ESI‡ for more details). Thus, removal of NO2(Ot) and/or NO2(CsN) from Cs8Nb6O19/[NO2(CsN)NO2(Ot)] with two NO2-adsorbates requires greater energy than removing them from Cs8Nb6O19/NO2(Ot) and/or Cs8Nb6O19/NO2(CsN). The overall energy of the reaction Cs8Nb6O19 + 2NO2 → Cs8Nb6O19/[NO2(CsN)NO2(Ot)] is ΔE/ΔH/ΔG = −77.4/−74.6/−58.0 kcal mol−1 (see Table 1). To summarize, a relatively weak coordination of the first NO2 radical to Cs8Nb6O19 at the Cs sites promotes stronger coordination of the second NO2 molecule at the Ot site of Cs8Nb6O19. As a result, the coordination of the NO2 radicals to Cs8Nb6O19 is substantially stronger than that of CO2, yet slightly weaker than that of one SO2 molecule.
The reported highly stable Cs8Nb6O19/[NO2(CsN)NO2(Ot)] complex with two NO2 fragments can also be formed via N–N bond activation of the coordinated N2O4 molecule by the polyoxometalate catalyst. The former pathway (i.e. stepwise addition of two NO2 radicals to polyoxoniobate) may be valid at ambient temperature, while the latter process may occur at low temperature. In this paper, we did not study the N–N activation barrier; however, we found that the complex Cs8Nb6O19/[NO2(CsN)NO2(Ot)] (see Fig. 3) lies significantly lower in energy than the Cs8Nb6O19 + N2O4 dissociation limit, by ΔE/ΔH/ΔG = 57.6/57.3/52.4 kcal mol−1, and ΔE/ΔH/ΔG = 37.8/40.0/46.8 kcal mol−1 lower than the Cs8Nb6O19/N2O4 intermediate.
In order to better understand the factors impacting the strength of the Cs8Nb6O19/NO2 interaction, we also analyzed the geometry of the complex Cs8Nb6O19/[NO2(CsN)NO2(Ot)]. As seen in Fig. 3, where we present the most important geometries of the Cs8Nb6O19/NO2(Ot), Cs8Nb6O19/NO2(CsN) and Cs8Nb6O19/[NO2(CsN)NO2(Ot)] species (for full geometries of these species, see the ESI‡), in Cs8Nb6O19/[NO2(CsN)NO2(Ot)], the Nb–Ot bond is elongated to 2.47 Å; concurrently, the Nb–OIN bonds (which are 2.34, 2.44 and 2.02 Å in these complexes, respectively) and N–Ot bonds (which are 1.28 and 2.25 Å in Cs8Nb6O19/[NO2(CsN)NO2(Ot)] and Cs8Nb6O19/NO2(Ot), respectively) are formed. As a result, the complex Cs8Nb6O19/[NO2(CsN)NO2(Ot)] has one NO3−δ fragment (δ = 0.4) and one NO2−δ fragment (δ = 0.94) coordinated to the Cs-cations.
Above, we have shown that: (1) at ambient temperatures, a relatively weak coordination of the first NO2 radical to Cs8Nb6O19 confers partial radical character on the polyoxoniobate and promotes a stronger coordination of the second NO2 radical to form a stable diamagnetic Cs8Nb6O19/[NO2(CsN)NO2(Ot)] complex, and (2) at low temperatures, coordination of a weakly stable N2O4 molecule to Cs8Nb6O19 followed by facile N–N bond activation leads to the same Cs8Nb6O19/[NO2(CsN)NO2(Ot)] complex. Regardless of the formation mechanisms, in Cs8Nb6O19/[NO2(CsN)NO2(Ot)], the coordination of the NO2 radical positioned at Ot to Cs8Nb6O19 is substantially stronger than that of CO2, yet is slightly weaker than that of one SO2 molecule.
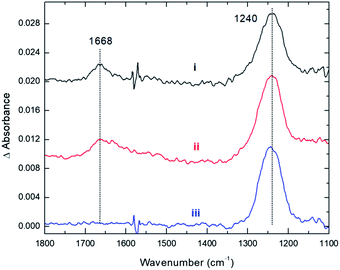
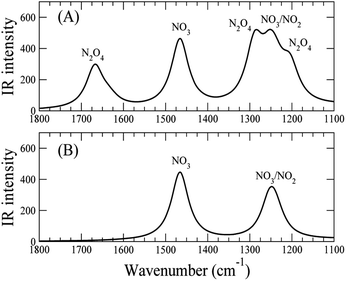
These conclusions from our computations are fully supported by experiments. As with CO2, the adsorption of NO2 onto Cs8Nb6O19 was probed with the use of infrared spectroscopy. Fig. 4 shows spectra for the interaction between NO2 and Cs8Nb6O19. The adsorption of NO2 on the surface resulted in two infrared vibrational features – one at 1668 cm−1 and another at 1240 cm−1 (Fig. 4, i). These features are attributed to adsorbate N–O stretches as opposed to POM motions, which appear below 1000 cm−1. Analysis of the calculated [Cs8Nb6O19]–NO2 complexes suggests that the 1668 cm−1 feature is likely due to an asymmetric NO stretch originating from the Cs8Nb6O19/N2O4 complex, which the calculations (unscaled) show to be at 1813 cm−1. For the other NO2 complexes, the highest frequency NO stretch is found below 1600 cm−1, i.e. at a lower frequency relative to the experimental peak. Taking into account the usual anharmonic correction, these modes will be found to be even further redshifted to lower frequencies. However, if we consider that the calculated asymmetric (strongly IR active) NO stretch of a free NO2 radical is 1752 cm−1, and the known experimental value25 is 1618 cm−1, the resulting frequency scale factor of 0.92 brings the asymmetric NO stretch of the Cs8Nb6O19/N2O4 complex to exactly 1668 cm−1. Moreover, if the measured 1668 and 1240 cm−1 peaks originate from the same thermal mixture of diamagnetic complexes, we expect that the 1240 cm−1 peak, which persists at higher temperatures (Fig. 4, iii), is due to the Cs8Nb6O19/[NO2(CsN)NO2(Ot)] complex, which is much more stable to thermal perturbation than Cs8Nb6O19/N2O4. The latter immediately transforms to Cs8Nb6O19/[NO2(CsN)NO2(Ot)] upon N–N activation by heating. Indeed, there is a group of IR-active NO stretching motions in the Cs8Nb6O19/[NO2(CsN)NO2(Ot)] complex in the 1346 to 1361 cm−1 (1238 to 1252 cm−1 scaled) region, which captures the measured 1240 cm−1 peak.
Thus, we present two spectra (shown in Fig. 5); one corresponds to low temperature, Fig. 5(A), which is the sum of Cs8Nb6O19/N2O4 and Cs8Nb6O19/[NO2(CsN)NO2(Ot)], and one corresponds to high temperature, Fig. 5(B), which is pure Cs8Nb6O19/[NO2(CsN)NO2(Ot)]. The frequency axis is scaled by the same factor of 0.92. The calculation is consistent with experiments with regard to the disappearance of the 1668 cm−1 peak and the persistence of the 1240 cm−1 peak. However, the peak at 1470 cm−1 (after scaling) in the calculated spectra, which is attributed to a local NO stretch of the NO3 unit in Cs8Nb6O19/[NO2(CsN)NO2(Ot)], is absent in the room-temperature experiments. This suggests that the formation of NO3 requires a significant amount of thermal energy.
Furthermore, experiments clearly show that NO2 is strongly bound to the POM, i.e. the 1240 cm−1 peak is present even after gas phase evacuation (Fig. 4, ii) and upon heating the POM to 423 K (Fig. 4, iii). In fact, thermal treatment up to 600 K was required to fully desorb the species, i.e. to remove NO2 radicals. This suggests that NO2 binds more strongly to the POM than CO2, which is consistent with the computational data for the Cs8Nb6O19/[NO2(CsN)NO2(Ot)] complex presented above (see Table 1 and the ESI‡).
Thus, the data presented above show that in the presence of ambient gas molecules of CO2, NO2 and SO2, Cs8Nb6O19 will absorb these molecules more strongly than the water and GB molecules required for hydrolysis of Sarin (see Table 1). This is expected to impact the hydrolysis of Sarin by Cs8Nb6O19 in the following two ways: first, because the ambient gas molecules coordinate to catalytically active Ot-centers, they block these catalytically active centers, hindering water and Sarin coordination, and may alter the previously reported mechanism of Sarin hydrolysis by Cs8Nb6O19. Second, the interaction of an ambient gas molecule with Cs8Nb6O19 may change the electronic properties of the polyoxoniobate: this is expected to only impact the calculated energetics of the Sarin hydrolysis and to not significantly change the nature of the previously reported intermediates and transition state structures.
Below, we test the first hypothesis by (a) studying the full potential energy surfaces of GB hydrolysis by Cs8Nb6O19/X, where X = CO2 and SO2, and (b) comparing these new findings with our previous results on the same reaction in the absence of ambient gas molecules. For the sake of simplicity, we discuss in detail only the reaction mechanism (as well as the structures of the pre-reaction complexes, intermediates, transition states and products) for X = CO2 and compare these findings with those (previously reported) in the absence of ambient gas molecules. In addition, we briefly discuss, where appropriate, our findings for X = SO2 (full potential energy surfaces are available in the ESI‡). The reactivities of the NO2 and other radical species coordinated to Cs8Nb6O19 will be reported elsewhere.
B. Hydrolysis of Sarin by Cs8Nb6O19/X species (where X = CO2 and SO2)
As we have shown previously24 and have briefly discussed above (see Scheme 1), Sarin hydrolysis by Cs8Nb6O19 is a multistep process, with coordination of a water molecule to the catalyst as the first step. The calculations (see Table 1) show that coordination of H2O to Cs8Nb6O19 to form Cs8Nb6O19/H2O is exothermic/exergonic by (presented as ΔH/ΔG) 23.6/17.3 kcal mol−1. In Cs8Nb6O19/H2O, the two hydrogens of the water molecule interact with one bridging (Oμ) and one terminal (Ot) oxygen atom of the polyoxometalate.Water molecule coordination to the adduct formed when CO2 (or SO2) binds to the Ot-center of Cs8Nb6O19 is a few kcal mol−1 less than that for “free” Cs8Nb6O19; the energies are −22.4/−11.9 and −21.0/−9.7 kcal mol−1 for X = CO2 and SO2, respectively. This effect is more pronounced for the Cs8Nb6O19/SO2 adduct than for Cs8Nb6O19/CO2. Furthermore, as seen in Fig. 6, the water coordination motif in Cs8Nb6O19/CO2/H2O is different from that in Cs8Nb6O19/H2O: because CO2 occupies the Ot-position in Cs8Nb6O19/CO2, the H2O molecule is H-bonded to one bridging (Oμ) and one CO (O1) oxygen atom (instead of Ot). The calculated Oμ–H1 and O1–H2 bond distances are 1.76 and 1.85 Å, respectively.
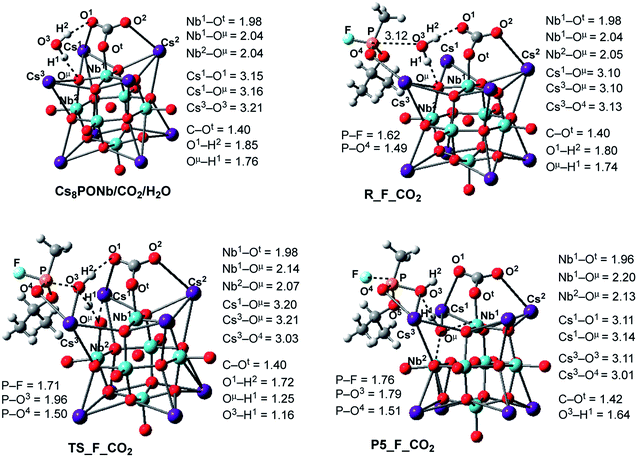 | ||
| Fig. 6 Calculated pre-reaction complexes, transition states and products of GB hydrolysis by Cs8Nb6O19/CO2 (i.e. the reaction Cs8Nb6O19/CO2 + H2O + GB → R-F_CO2 → TS-F_CO2 → P5-F_CO2) and their important geometry parameters (in Å). Similar structures for X = SO2 are presented in the ESI.‡ | ||
Following the formation of the Cs8Nb6O19/X/H2O complex, the addition of Sarin to this intermediate occurs. Previously, we examined several approaches of Sarin to Cs8Nb6O19 and found that nerve agent decomposition occurs when Sarin approaches the hydrated Cs8Nb6O19 segment with its O(sp2) and O(sp3) atoms (labeled in Fig. 6 and below as O5 and O4, respectively).24 The additional stabilization of the complex arises from the long-range O4⋯Cs3 ionic interaction. Thus, for the purposes of modeling the decomposition of Sarin in the presence of carbon and sulfur dioxide, it is sufficient to examine the most energetically favorable pathway, similar to that previously reported for the case with no ambient gas molecules. In keeping with the previously established shorthand notation, the pre-reaction complex of this reaction pathway is labeled as R–F_X.
The present calculations show that the coordination of Sarin (GB) to Cs8Nb6O19/X/H2O is exothermic by −18.0/−2.4 and −17.4/−3.8 kcal mol−1 for X = CO2 and SO2, respectively. Inspection of the structure of the Cs8Nb6O19/X/H2O/GB, R–F_X, intermediate reveals a non-covalently bonded [Cs8Nb6O19/CO2/H2O]–GB complex. For example, as seen in Fig. 6, in contrast to the coordination of GB to Cs8Nb6O19/H2O, in Cs8Nb6O19/CO2/H2O/GB, the nerve agent is coordinated to one of the Cs centers of the Cs8Nb6O19-core with its P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O4 double bond. Several H-bonds also exist between the GB ligand and the [Cs8Nb6O19/CO2/H2O]-fragment. In this complex, the calculated Cs3–O4 bond distance is 3.13 Å and the nascent P–O3(OH2) bond distance is 3.12 Å.
O4 double bond. Several H-bonds also exist between the GB ligand and the [Cs8Nb6O19/CO2/H2O]-fragment. In this complex, the calculated Cs3–O4 bond distance is 3.13 Å and the nascent P–O3(OH2) bond distance is 3.12 Å.
In the next step, hydrolysis of the coordinated water molecule occurs between the coordinated gas molecule X, the bridging oxygen (Oμ) of the Cs8Nb6O19-core and the phosphorus center of Sarin. The transition state associated with this process, TS-F_CO2, is shown in Fig. 6 (for TS-F_SO2, see the ESI‡). As seen in this figure, at TS-F_CO2, the breaking O3–H1 bond of the water molecule is elongated to 1.16 Å, and the forming Oμ–H1 bond distance becomes 1.25 Å. In addition, Nb1–Oμ and Nb2–Oμ bonds are slightly elongated and the Cs3–O4 bond is slightly shortened. Importantly, the Cs3-center of the Cs8Nb6O19 core also interacts with the oxygen (O3) of water and provides additional support for hydrolysis. Here, the other coordinates of interest are the P–O3(H2O) bond and the P–F bond.
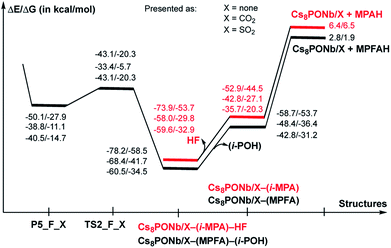
As seen in Fig. 6, P–O3(H2O) undergoes a major reduction from 3.12 Å in R-F_CO2 to 1.96 Å in TS-F_CO2. Its P-F counterpart, located trans to the water-activated molecule, extends from the typical single bond in R-F_CO2, with an increase from 1.62 Å to 1.71 Å in TS-F_CO2. Similar geometry changes at the hydrolysis transition state were observed for X = SO2 (see the ESI‡). As seen in Fig. 7, the calculated ΔE/ΔG barrier heights relative to R-F_X are 7.8/7.5 and 8.4/8.8 kcal mol−1 for X = CO2 and SO2, respectively. These values are slightly larger than the values of 6.8/6.1 kcal mol−1 calculated for the reaction in the absence of these ambient gas molecules; this suggests that common battlefield contaminants may impair the hydrolytic decomposition of nerve agents under operational conditions.
The hydrolysis product is a pentacoordinated-phosphorus complex P5-F_X with a trigonal bipyramidal structure around the central phosphorus atom. In our previous paper, we showed that this intermediate exhibits multiple isomeric forms.24 Here, we discuss only the energetically most favorable form, which is directly connected to the transition state TS-F_X. For example, as seen in Fig. 6, the formed P–O3 bond in P5-F_CO2 contracts to 1.79 Å, while its P-F counterpart, located trans to the activated water molecule, extends to 1.76 Å. The broken O3–H1 bond is elongated to 1.64 Å and the Nb1–Oμ and Nb2–Oμ bonds are elongated to 2.20 and 2.13 Å, respectively. Concurrently, the Cs3–O3 bond of 3.11 Å is formed to provide additional stabilization to the pentacoordinated-phosphorus complex, similar to that previously reported in P5-F.24 Based on the calculated Mulliken charge distribution, the resulting P5-F_X complexes can be labeled as a [(GBOH−)–(Cs8Nb6O19H/X)+] ion-pair system.
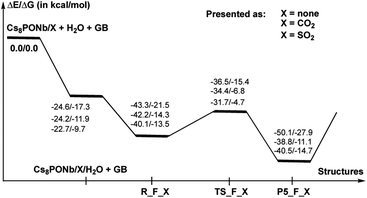
As shown in Fig. 7, the hydrolysis of Sarin, i.e. the reaction Cs8Nb6O19/X + H2O + GB → R-F_X → TS-F_X → P5-F_X for X = none, CO2 or SO2, is exergonic by −50.1/−27.9, −38.8/−11.1 and −40.5/−14.7 kcal mol−1 (presented as ΔH/ΔG) and proceeds over energy barriers of 6.8/6.1, 7.5/7.5 and 8.4/8.8 kcal mol−1 (calculated relative to the pre-reaction intermediate R-F_X), respectively. The reaction R-F_X → TS-F_X → P5-F_X is exothermic for X = none and SO2 by 6.8/6.4 and 0.4/1.2 kcal mol−1, respectively, but is endothermic by 3.4/3.2 kcal mol−1 for X = CO2. These energy values allow us to conclude that the presence of ambient gas molecules increases the energies of the stationary points relative to the asymptote of the reactants. This is likely the result of a different charge distribution on Cs8Nb6O19/X relative to Cs8Nb6O19, where X acquires a net negative charge of 0.8 to 0.7 |e|, as we showed above. Furthermore, X coordinates to the Ot reactive center and disables its hydrolytic activity. The presence of ambient gases increases the hydrolysis barrier by 1.0 to 2.5 kcal mol−1, and this change in the energy barrier is closely associated with the Cs8Nb6O19–X complexation energy: the stronger the Cs8Nb6O19–X bond, the higher the barrier for Sarin hydrolysis.
C. Pentacoordinated P5-F_X intermediate dissociation
Once the pentacoordinated P5-F_X species is formed, the reaction can proceed along several paths, as discussed in our previous paper.24 In order to evaluate the role of the catalyst in the course of the reaction, as above, here we discuss in detail only those pathways that directly involve the catalyst. These are the HF and isopropanol elimination and, ultimately, desorption pathways. The accompanying products of these paths are isopropyl methyl phosphonic acid (i-MPA) and methyl phosphonofluoridic acid (MPFA), respectively. It is evident that in order to form HF or isopropanol, protonation of the fluoride or oxygen centers of the isopropoxy ligand is required. Furthermore, in order to facilitate regeneration of the catalyst, the ultimate proton source should be the OμH1-group of the [Cs8Nb6O19H/X]+ cation. However, these processes are expected to be very complex and may proceed via multiple mechanisms. One of these processes could involve any surrounding water molecules, which are expected to be present in real experimental conditions. In this mechanism, a water molecule located close to the fluoride or oxygen atoms of the iopropoxy ligand is expected to donate its proton to these groups (to form HF and/or isopropanol, respectively) and compensate by removing the proton from the OμH1-group of the catalyst via a H-bonding network. This process depends on multiple factors (including, but not limited to, the concentration of water in the system and the reaction temperature) and was not studied in this paper.Another possible mechanism of HF and/or isopropanol formation is direct removal of the proton from the OμH1-group of the catalyst by the fluoride and/or isopropoxide ligands, respectively. As shown previously for the Cs8Nb6O19 catalyst (i.e., in the absence of ambient gas molecules),24 these processes occur with very small energy barriers which have no contribution to the overall outcome of the decontamination reaction but lead to the most energetically stable intermediates, Cs8Nb6O19-(i-MPA)-HF and Cs8Nb6O19-(MPFA)-(i-POH), respectively (see Fig. 8). Here, we performed an extensive search to locate the transition states TS2-F_HF_X and TS2-F_(i-POH)_X that lead to either HF and i-MPA or isopropanol (i-POH) and MPFA from the most stable pentacoordinated intermediate P5-F_X (where X = CO2 or SO2). Ultimately, we were able to locate only the TS2-F_(i-POH)_X transition state (see Fig. 8). The search for the HF formation transition state TS2-F_HF_X was unsuccessful and always led to either the Cs8Nb6O19/X-(i-MPA)-HF intermediate, its derivative F−⋯H+⋯Oμ intermediate, or the pre-reaction complex P5-F_X. For example, in Fig. 8, we present the intermediates, transition states and products involved in pentacoordinated P5-F_CO2 intermediate dissociation alone, with their important geometry parameters (for those of X = SO2, see the ESI‡). The relative energies of these species, calculated from the P5-F_X pre-reaction complex, are given in Fig. 9.
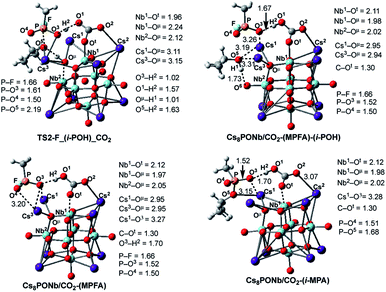 | ||
| Fig. 8 The calculated transition states, intermediates and products of the dissociation of pentacoordinated P5-F_CO2 (i.e. reactions: P5-F_CO2 → Cs8Nb6O19/CO2-(MPFA)-(i-POH) → Cs8Nb6O19/CO2 + MPFAH + (i-POH) and P5-F_X → Cs8Nb6O19/CO2-(MPA)-HF → Cs8Nb6O19/CO2 + MPAH + HF) with their important geometry parameters (in Å). Similar structures for X = SO2 are presented in the ESI.‡ | ||
As seen in Fig. 8, at the transition state TS2-F_(i-POH)_CO2 associated with the formation of i-POH and MPFA, the activated P–O5(Osp2) bond extends to 2.19 Å from 1.68 Å in P5-F_CO2, with simultaneous formation of a double H-bond network (O5–H1 = 1.63 Å and O1–H2 = 1.57 Å) as a precursor to the charge-preserving double proton transfer. In other words, as the proton of the OμH1-group moves to Sarin, the proton on the PO3H1 group of Sarin migrates back to the Cs8Nb6O19/X-core to form [HXOt]q, where X = CO2. As a result, the formed P–O3(H2O) bond is shortened from 1.79 Å in P5-F_CO2 to 1.61 Å in the transition state.
As seen in Fig. 9, the calculated energy barriers from P5-F_X are 7.0/7.6, 5.4/5.4 and 3.6/6.5 kcal mol−1 for X = none, CO2 and SO2. Thus, the presence of these gas molecules in the reaction mixture slightly reduces the pentacoordinated P5-F_X intermediate dissociation barrier (by 2 to 4 kcal mol−1). Furthermore, the changes in the i-POH and MPFA formation energy barriers correlate with the Cs8Nb6O19–X complexation energy: the stronger the Cs8Nb6O19–X bond, the smaller the i-POH and MPFA formation energy barriers.
Comparison of the calculated energetics for the dissociation of the pentacoordinated intermediate with those for hydrolysis (i.e. formation of the pentacoordinated intermediate) show that, in general, the hydrolysis step is a rate-determining step for all reported species, and the presence of ambient gas molecules increases this energy barrier only slightly, by 2 to 4 kcal mol−1. Furthermore, the height of this rate-determining energy barrier correlates with the Cs8Nb6O19–X complexation energy: the stronger the Cs8Nb6O19–X bond, the more difficult the hydrolysis of GB by the Cs8Nb6O19 catalyst.
D. Catalyst regeneration
Thus, the facile dissociation of the P5_F_X species, as reported previously for P5_F, yields HF and i-MPA and/or i-POH and MPFA products. All these species are initially bound to Cs8Nb6O19, as shown in Fig. 8 for X = CO2 and the ESI‡ for X = SO2. For example, in the Cs8Nb6O19/CO2-(i-MPA)-HF complex, the (i-MPA)-fragment forms a hydrogen bond with the Oμ and OH-unit of the HOCOOt fragment, respectively. The HF molecule, on the other hand, in the presence of an X molecule, prefers to form an [F−⋯H+] ion-pair prior to dissociation. Similarly, in the Cs8Nb6O19/CO2-(MPFA)-(i-POH) complex, the (i-POH) molecule and MPFA-fragment are hydrogen bonded to another Ot atom and the OH-unit of the HOCOOt fragment, respectively: the calculated H1–O6 and O3–H2 bond distances are 1.73 and 1.67 Å, respectively. In addition, there are electrostatic interactions between the O center of the isopropanol molecule and two Cs cations of the Cs8Nb6O19/CO2 core, with Cs1–O5 and Cs3–O5 bond distances of 3.19 Å and 3.31 Å, respectively. The formed P–O3 fragment also interacts with the Cs1-center, with a Cs1–O3 distance of 3.16 Å.As seen in Fig. 9, the formed Cs8Nb6O19/X-MPFA-(i-POH) is the energetically lowest structure on the potential energy surface of the entire GB hydrolysis and decontamination reaction by Cs8Nb6O19 both in the absence and presence of ambient gas molecules. The intermediate Cs8Nb6O19/X-(i-MPA)-HF is found to be only slightly higher in energy. As we mentioned previously,24 the high stability of these intermediates is due in part to the strong hydrogen bonds between the adsorbates and the Cs8Nb6O19/X-core; however, it is also due to the additional stabilizing interactions between the Cs counter-ions and the electronegative atoms of the nerve-agent fragments.
Desorption of HF and isopropanol from Cs8Nb6O19/X-(i-MPA)-HF and Cs8Nb6O19/X-MPFA-(i-POH) requires 15.2/12.7 and 20.0/5.3 kcal mol−1 energy, respectively, for X = CO2. Dissociation of HF and isopropanol only slightly modifies the geometries of the products Cs8Nb6O19/X-(i-MPA) and Cs8Nb6O19/X-MPFA fragments (for example, see Fig. 8 for X = CO2) compared with the Cs8Nb6O19/X-(i-MPA)-HF and Cs8Nb6O19/X-MPFA-(i-POH) adducts; therefore, this will not be discussed in detail.
However, both i-MPA in Cs8Nb6O19/X-(i-MPA) and MPFA in Cs8Nb6O19/X-MPFA are strongly bound to the protonated [Cs8Nb6O19/X]H+-core. Thus, regeneration of the catalyst requires deprotonation of the [Cs8Nb6O19/X]H+-core and protonation of the phosphonic acids i-MPA and MPFA. This step of the reaction, which forms a final decontaminated form of the GB and re-generated catalyst, is found to be highly endothermic/endergonic, i.e. 6.4/6.5 and 2.8/1.9 kcal mol−1 for i-MPAH and MPFAH formation, respectively. Overall, the last steps of the reaction, i.e. the reactions Cs8Nb6O19/X-(i-MPA)-HF → Cs8Nb6O19/X + HF + (i-MPAH) and Cs8Nb6O19/X-MPFA-(i-POH) → Cs8Nb6O19/X + (i-POH) + MPFAH, are highly prohibitive and require energies of 80.3/60.2 (X = none), 64.4/36.3 (X = CO2), and 66.0/39.4 (X = SO2) kcal mol−1 and 81.0/60.4 (X = none), 71.2/43.6 (X = CO2), and 63.3/36.4 (X = SO2) kcal mol−1, respectively. Furthermore, deprotonation of the [Cs8Nb6O19/X]H+-core and protonation of the phosphonic acids i-MPA and MPFA is expected to be very complex and may proceed via several pathways depending on the reaction conditions. One of these may involve any surrounding water molecules, in real experimental conditions, via a concerted protonation-deprotonation mechanism involving the hydrogen-bonded water-based network. However, this process depends on multiple factors (including, but not limited to, the concentration of water in the system and the reaction temperature) and was not studied in this paper. We also failed to locate a transition state associated with the direct deprotonation of [Cs8Nb6O19/X]H+ and protonation of the phosphonic acids because of the high stability of the corresponding pre-reaction complexes Cs8Nb6O19/X-(i-MPA) and Cs8Nb6O19/X-MPFA. The solution to this issue requires special comprehensive experimental and computational studies, which are in progress.
Conclusions
This paper, for the first time, addresses the impact of environmentally-significant ambient gas molecules, NO2, CO2 and SO2, on the structure, stability and decontamination activity of a basic polyoxometalate species. Specifically, Cs8Nb6O19 in the presence of these gases has been studied in depth by complementary computational and experimental approaches. It was found that:(1) Cs8Nb6O19 absorbs ambient gas molecules of X = CO2, NO2 and SO2 more strongly than it absorbs water or Sarin (GB) molecules. The calculated Cs8Nb6O19–X binding energy follows the trend for ΔG (X = CO2) < ΔG (NO2) < ΔG (SO2).
(2) The impacts of the diamagnetic CO2 and SO2 molecules on polyoxoniobate Cs8Nb6O19 are fundamentally different than that of the NO2 radical. At ambient temperatures, weak coordination of the first NO2 radical to Cs8Nb6O19 confers partial radical character on the polyoxoniobate and promotes a stronger coordination of the second NO2 radical to form a stable diamagnetic Cs8Nb6O19/(NO2)2 species; meanwhile, at low temperatures, NO2 radicals form weakly stable dinitrogen tetraoxide (N2O4), which interacts weakly with Cs8Nb6O19.
(3) Similar to the case without ambient gas molecules, reported previously,24 in the presence of X, GB hydrolysis by Cs8Nb6O19/X proceeds via general base hydrolysis involving: (a) adsorption of water and the nerve agent on the Cs8Nb6O19/X catalyst, (b) concerted hydrolysis of the adsorbed water molecule on a basic oxygen atom of the polyoxoniobate and nucleophilic addition of the nascent OH group to the phosphorus center of the nerve agent, (c) rapid reorganization of the resulting pentacoordinated-phosphorus intermediate followed by dissociation of either HF or isopropanol with formation of POM-bound isopropyl methyl phosphonic acid (i-MPA) or methyl phosphonofluoridic acid (MPFA), respectively.
(4) Cs8Nb6O19 adsorbs ambient gas molecules X at its basic Ot (or Oμ) reactive centers, which shields them from involvement in the base hydrolysis. As a result, one of the O centers of the coordinated ambient gas molecule becomes an active hydrolysis center. This increases the energies of the stationary points relative to the asymptote of the reactants and increases the hydrolysis barrier. These changes are closely correlated with the Cs8Nb6O19–X complexation energy; the stronger the Cs8Nb6O19–X bond, the higher the barrier for Sarin hydrolysis.
(5) The most energetically stable products of the GB hydrolysis and decontamination reaction are Cs8Nb6O19/X-MPFA-(i-POH) and Cs8Nb6O19/X-(i-MPA)-HF both in the absence and presence of ambient gas molecules. The high stability of these intermediates is due in part to the strong hydrogen bonds between the adsorbates and the protonated [Cs8Nb6O19/X/H]+-core and to interactions between the Cs counterions and the electronegative atoms of the adsorbates.
(6) Desorption of HF or/and (i-POH) and regeneration of the catalyst requires deprotonation of the [Cs8Nb6O19/X/H]+-core with protonation of the phosphonic acids i-MPA and MPFA. Regeneration of the catalyst is a highly endergonic process and is the rate-limiting step for GB hydrolytic decontamination, both in the absence and presence of ambient gas molecules.
Notes
A. Computational and experimental procedures
Infrared spectroscopic experiments were performed in a stainless-steel high-vacuum chamber with a base pressure of ∼1 × 10−8 Torr. The Cs8Nb6O19 sample was pressed, as a 7 mm diameter disk, into a tungsten grid, which was then clamped onto a sample mount coupled to a precision manipulator. An empty region of the grid was used to monitor the gas phase species in the chamber and was also employed as a background for surface adsorption and desorption studies. The grid was resistively heated, and the temperature was monitored via a K-type thermocouple spot-welded adjacent to the sample. A PID controller mediated the sample temperature to within ±1 K. Details of the vacuum chamber and sample mount can be found in a previous publication.29 An FTIR spectrometer (Thermo, Nicolet, Nexus 470 FTIR) with an external liquid-N2-cooled MCT-A detector and a spectral resolution of 2 cm−1 was used for collection of the infrared spectra.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This material is based upon work supported by the U. S. Army Research Laboratory and the U. S. Army Research Office under grant number W911NF-15-2-0107. The authors are grateful for the support of the Defence Threat Reduction Agency. The authors gratefully acknowledge NSF MRI-R2 grant (CHE-0958205 for D. G. M.) and the use of the resources of the Cherry Emerson Center for Scientific Computation.Notes and references
- (a) F. M. Raushel, Nature, 2011, 469, 310 CrossRef CAS PubMed; (b) M. Enserink, Science, 2013, 341, 1050 CrossRef CAS PubMed; (c) M. B. D. Nikitin, P. K. Kerr and A. Feickert, Syria's Chemical Weapons: Issues for Congress, 2013, report # R42848 Search PubMed.
- (a) N. Sharma and R. Kakkar, Adv. Mater. Lett., 2013, 4, 508 CrossRef; (b) N. Munro, Environ. Health Perspect., 1994, 102, 18 CrossRef CAS PubMed; (c) W. W. George, in Nanoscale Materials in Chemistry: Environmental Applications, American Chemical Society, 2010, vol. 1045, pp. 125–136 Search PubMed.
- R. H. Pastel and E. C. Ritchie, in Psychological Responses to the New Terrorism: A NATO-Russia Dialogue, IOS Press, Amsterdam, 2005, pp. 9–24 Search PubMed.
- (a) Y. J. Yang, K. Kim, O. G. Tsay, D. A. Atwood and D. G. Churchill, Chem. Rev., 2015, 115, PR1 CrossRef PubMed; (b) Y. C. Yang, J. A. Baker and J. R. Ward, Chem. Rev., 1992, 92, 1729 CrossRef CAS.
- J. B. DeCoste and G. W. Peterson, Chem. Rev., 2014, 114, 5695 CrossRef CAS PubMed.
- S. Y. Moon, G. W. Wagner, J. E. Mondloch, G. W. Peterson, J. B. DeCoste, J. T. Hupp and O. K. Farha, Inorg. Chem., 2015, 54, 10829 CrossRef CAS PubMed.
- Y. Liu, S. Y. Moon, J. T. Hupp and O. K. Farha, ACS Nano, 2015, 9, 12358 CrossRef CAS PubMed.
- J. E. Mondloch, M. J. Katz, W. C. Isley, P. Ghosh, P. L. Liao, W. Bury, G. W. Wagner, M. G. Hall, J. B. DeCoste, G. W. Peterson, R. Q. Snurr, C. J. Cramer, J. T. Hupp and O. K. Farha, Nat. Mater., 2015, 14, 512 CrossRef CAS PubMed.
- M. J. Katz, J. E. Mondloch, R. K. Totten, J. K. Park, S. T. Nguyen, O. K. Farha and J. T. Hupp, Angew. Chem., Int. Ed., 2014, 53, 497 CrossRef CAS PubMed.
- R. Gaillac, P. Pullumbi, K. A. Beyer, K. W. Chapman, D. A. Keen, T. D. Bennett and F.-X. Coudert, Nat. Mater., 2017, 16, 1149–1154 CrossRef CAS PubMed.
- M. K. Kinnan, W. R. Creasy, L. B. Fullmer, H. L. Schreuder-Gibson and M. Nyman, Eur. J. Inorg. Chem., 2014, 2014, 2361 CrossRef CAS.
- W. Guo, H. Lv, K. P. Sullivan, W. O. Gordon, A. Balboa, G. W. Wagner, D. G. Musaev, J. Bacsa and C. L. Hill, Angew. Chem., Int. Ed., 2016, 55, 7403 CrossRef CAS PubMed.
- (a) D. M. Mizrahi, S. Saphier and I. Columbus, J. Hazard. Mater., 2010, 179, 495 CrossRef CAS PubMed; (b) N. M. Okun, J. C. Tarr, D. A. Hilleshiem, L. Zhang, K. I. Hardcastle and C. L. Hill, J. Mol. Catal. A: Chem., 2006, 246, 11 CrossRef CAS; (c) N. M. Okun, T. M. Anderson and C. L. Hill, J. Mol. Catal. A: Chem., 2003, 197, 283 CrossRef CAS; (d) F. Carniato, C. Bisio, R. Psaro, L. Marchese and M. Guidotti, Angew. Chem., Int. Ed., 2014, 53, 10095 CrossRef CAS PubMed.
- As an example for computational studies of the POMs see: (a) J. M. Poblet, X. Lopez and C. Bo, Chem. Soc. Rev., 2003, 32, 297 RSC; (b) P. Miro, J. M. Poblet, J. B. Avalos and C. Bo, Can. J. Biochem., 2009, 87, 1296 CrossRef CAS; (c) C. Bo and J. M. Poblet, Isr. J. Chem., 2011, 51, 228 CrossRef CAS; (d) X. Lopez, P. Miro, J. J. Carbo, A. Rodriguez-Fortea, C. Bo and J. M. Poblet, Theor. Chem. Acc., 2011, 128, 393 CrossRef CAS; (e) X. Lopez, J. J. Carbo, C. Bo and J. M. Poblet, Chem. Soc. Rev., 2012, 41, 7537 RSC; (f) B. Matt, X. Xiang, A. L. Kaledin, N. N. Han, J. Moussa, H. Amouri, S. Alves, C. L. Hill, T. Q. Lian, D. G. Musaev, G. Izzet and A. Proust, Chem. Sci., 2013, 4, 1737 RSC; (g) A. E. Kuznetsov, Y. V. Geletii, C. L. Hill, K. Morokuma and D. C. Musaev, J. Am. Chem. Soc., 2009, 131, 6844 CrossRef CAS PubMed.
- J. Song, Z. Luo, D. K. Britt, H. Furukawa, O. M. Yaghi, K. I. Hardcastle and C. L. Hill, J. Am. Chem. Soc., 2011, 133, 16839 CrossRef CAS PubMed.
- F. J. Ma, S. X. Liu, C. Y. Sun, D. D. Liang, G. J. Ren, F. Wei, Y. G. Chen and Z. M. Su, J. Am. Chem. Soc., 2011, 133, 4178 CrossRef CAS PubMed.
- T. J. Bandosz, M. Laskoski, J. Mahle, G. Mogilevsky, G. W. Peterson, J. A. Rossin and G. W. Wagner, J. Phys. Chem. C, 2012, 116, 11606 CAS.
- S. W. Yang, D. C. Doetschman, J. T. Schulte, J. B. Sarnbur, C. W. Kanyi and J. D. Fox, Microporous Mesoporous Mater., 2006, 92, 56 CrossRef CAS.
- L. Bromberg, H. Schreuder-Gibson, W. R. Creasy, D. J. McGarvey, R. A. Fry and T. A. Hatton, Ind. Eng. Chem. Res., 2009, 48, 1650 CrossRef CAS.
- (a) M. K. Kinnan, W. R. Creasy, L. B. Fullmer, H. L. Schreuder-Gibson and M. Nyman, Eur. J. Inorg. Chem., 2014, 2014, 2361 CrossRef CAS; (b) F.-J. Ma, S.-X. Liu, C.-Y. Sun, D.-D. Liang, G.-J. Ren, F. Wei, Y.-G. Chen and Z.-M. Su, J. Am. Chem. Soc., 2011, 133, 4178 CrossRef CAS PubMed; (c) D. M. Mizrahi, S. Saphier and I. Columbus, J. Hazard. Mater., 2010, 179, 495–499 CrossRef CAS PubMed; (d) N. M. Okun, J. C. Tarr, D. A. Hilleshiem, L. Zhang, K. I. Hardcastle and C. L. Hill, J. Mol. Catal. A: Chem., 2006, 246, 11 CrossRef CAS; (e) N. M. Okun, T. M. Anderson and C. L. Hill, J. Mol. Catal. A: Chem., 2003, 197, 283 CrossRef CAS; (f) F. Carniato, C. Bisio, R. Psaro, L. Marchese and M. Guidotti, Angew. Chem., Int. Ed., 2014, 53, 10095 CrossRef CAS PubMed.
- (a) T. Yamase and M. T. Pope, in Nanostructure Science and Technology, ed. D. J. Lockwood, Kluwer Academic/Plenum Publishers, New York, vol. 2, 2002 Search PubMed; (b) M. T. Pope, in Comprehensive Coordination Chemistry II: From Biology to Nanotechnology, ed. A. G. Wedd, Elsevier Ltd., Oxford, UK, 2004, vol. 4, pp. 635–678 Search PubMed; (c) H. N. Miras, J. Yan, D.-L. Long and L. Cronin, Chem. Soc. Rev., 2012, 41, 7403 RSC; (d) H. Lv, Y. V. Geletii, C. Zhao, J. W. Vickers, G. Zhu, Z. Luo, J. Song, T. Lian, D. G. Musaev and C. L. Hill, Chem. Soc. Rev., 2012, 41, 7572 RSC.
- (a) M. R. Antonio, M. Nyman and T. M. Anderson, Angew. Chem., Int. Ed., 2009, 121, 6252 CrossRef; (b) M. Nyman, T. M. Alam, F. Bonhomme, M. A. Rodriguez, C. S. Frazer and M. E. Welk, J. Cluster Sci., 2006, 17, 197 CrossRef CAS; (c) M. Nyman, Dalton Trans., 2011, 40, 8049 RSC; (d) E. M. Villa, C. A. Ohlin, E. Balogh, T. M. Anderson, M. D. Nyman and W. H. Casey, Angew. Chem., Int. Ed., 2008, 47, 4844 CrossRef CAS PubMed; (e) E. Balogh, T. M. Anderson, J. R. Rustad, M. Nyman and W. H. Casey, Inorg. Chem., 2007, 46, 7032 CrossRef CAS PubMed.
- M. Nyman, F. Bonhomme, T. M. Alam, M. A. Rodriguez, B. R. Cherry, J. L. Krumhansl, T. M. Nenoff and A. M. Sattler, Science, 2002, 297, 996 CrossRef CAS PubMed.
- R. C. Chapleski Jr, D. G. Musaev, C. L. Hill and D. Troya, J. Phys. Chem. C, 2016, 120, 16822 Search PubMed.
- T. Shimanouchi, Tables of molecular vibrational frequencies, National Bureau of Standards, U.S. Govt. Print. Off., Washington, 1972 Search PubMed.
- (a) H. A. Bent, Inorg. Chem., 1963, 2, 747 CrossRef CAS; (b) E. Wiberg, N. Wiberg and A. F. Holleman, Inorganic Chemistry, Academic Press, San Diego, 2001, ISBN 0-12-352651-5 Search PubMed.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. β. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, A. Dapprich, A. D. Daniels, ñ. n. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian, Inc.: Wallingford, CT, USA, 2009.
- P. Basu, T. H. Ballinger and J. T. Yates, Rev. Sci. Instrum., 1988, 59, 1321 CrossRef CAS.
Footnotes |
| † Dedicated to the memory of Prof. Keiji Morokuma. |
| ‡ Electronic supplementary information (ESI) available: (1) The calculated transition states, intermediates and products of the GB hydrolysis and their important geometry parameters (in Å) for X = SO2, (2) the calculated adsorption energies (in kcal mol−1) of NO2 radicals to Cs8Nb6O19, (3) Cartesian coordinates for all reported structures in xyz format. (structure.xyz). See DOI: 10.1039/c7sc04997h |
| This journal is © The Royal Society of Chemistry 2018 |