Open Access Article
Open Access ArticleThe TensorMol-0.1 model chemistry: a neural network augmented with long-range physics†
Kun
Yao
 ,
John E.
Herr
,
David W.
Toth
,
John E.
Herr
,
David W.
Toth
 ,
Ryker
Mckintyre
and
John
Parkhill
,
Ryker
Mckintyre
and
John
Parkhill
 *
*
Dept. of Chemistry and Biochemistry, The University of Notre Dame du Lac, USA. E-mail: john.parkhill@gmail.com
First published on 18th January 2018
Abstract
Traditional force fields cannot model chemical reactivity, and suffer from low generality without re-fitting. Neural network potentials promise to address these problems, offering energies and forces with near ab initio accuracy at low cost. However a data-driven approach is naturally inefficient for long-range interatomic forces that have simple physical formulas. In this manuscript we construct a hybrid model chemistry consisting of a nearsighted neural network potential with screened long-range electrostatic and van der Waals physics. This trained potential, simply dubbed “TensorMol-0.1”, is offered in an open-source Python package capable of many of the simulation types commonly used to study chemistry: geometry optimizations, harmonic spectra, open or periodic molecular dynamics, Monte Carlo, and nudged elastic band calculations. We describe the robustness and speed of the package, demonstrating its millihartree accuracy and scalability to tens-of-thousands of atoms on ordinary laptops. We demonstrate the performance of the model by reproducing vibrational spectra, and simulating the molecular dynamics of a protein. Our comparisons with electronic structure theory and experimental data demonstrate that neural network molecular dynamics is poised to become an important tool for molecular simulation, lowering the resource barrier to simulating chemistry.
1 Introduction
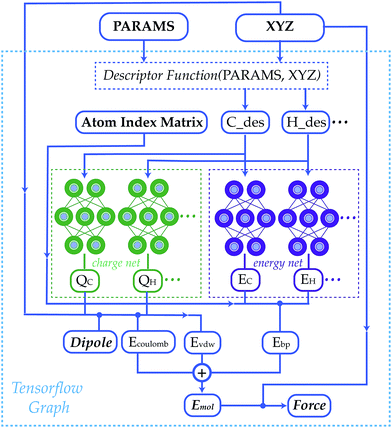
Statistical models from machine learning experienced growing popularity in many areas of chemistry, such as in reducing the cost of simulating chemical systems,1–13 improving the accuracy of quantum methods,14–22 generating force field parameters,23,24 predicting molecular properties25–32 and designing new materials.33–38 Neural network model chemistries (NNMCs) are one of the most powerful methods among this class of models.39–45 They are shown to be capable of generating high quality potential energy surfaces (PESs) with different schemes such as summing over atoms or bonds,46–57 many-body expansions58–60 and permutation invariant polynomials.61–64 They are also used to predict the properties of materials,65–73 and even to find new drugs.74–79 In spite of their growing popularity, traditional force fields remain more popular than NNMCs, even for screening and reactive applications. This paper develops an open-source, transferable neural network model chemistry called TensorMol-0.1 (Fig. 1). This model hybridizes a NNMC with the physical contributions to molecular energies that are familiar from Molecular Mechanics and corrections to Density Functional Theory (DFT).80 This approach yields a predictable reproduction of physical long-range forces, and features a linear-scaling inductive charge model. The charges do not depend on a quadratic-scaling polarization equation like a Thole-model,81 instead they are not fixed and respond well to geometry changes as we will show with reproduction of IR spectra.Our group is one of several who have been pursuing transferable and black-box neural network model chemistries.7,16,46,50,54,82,83 The state of the art in this field is progressing rapidly. Readers may not appreciate that a model can achieve chemical accuracy for energies but have uselessly noisy forces. Models that provide energies at equilibrium, and those treating a fixed molecule or stoichiometry, are nowadays reliably produced.50 We will show that TensorMol-0.1 yields usefully accurate predictions of forces out-of-equilibrium by showing the reproduction of infrared spectra that closely approximate our source model chemistry (ωB97X-D, 6-311G**),84 and molecular dynamics. We outline several tricks that are required to ensure the stability of long-time molecular dynamics.
This force model is implemented in an open-source package that uses the TensorFlow tensor algebra system to compute descriptors and forces. The methodology can be used to propagate the dynamics of large molecules (105 atoms) on simple laptop computers. No force field refinement, atom assignment, or other interventions are needed to apply the method to a molecule of interest, so long as the elements are supported. The package is also interfaced with the I-PI path integral package,85 to allow for quantum simulations and enhanced sampling.
2 Methods
The community of neural network model chemistry developers is rapidly improving the accuracy and generality of these reactive force fields.4,48,49,63,82,86 The model developed in this paper includes several components that were the subject of recent developments in other groups.46,49,52,82,87 We will describe the details here from the bottom up, citing prior studies. Our notational convention will be that i, j, k… are the indices of atoms, qi is the charge on atom i, x, y and z are atomic numbers, A, B and C are molecules, and α, β… are the indices of basis functions which are the products of radial and angular functions. If a function depends on all the atomic coordinates of a molecule it will be written as a vector, and those functions which depend on only a few coordinates will be given explicit indices. The energy of TensorMol-0.1 is expressed as a sum of a short-range embedded n-body potential,49 long-range electrostatic potential and van der Waals force: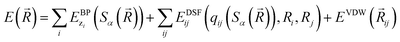 | (1) |
In the above expression Ezi is a Behler–Parinello type energy network for the element z for atom i. This n-body potential takes as its argument Sα, the modified symmetry functions of Isayev and coworkers:82
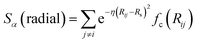 | (2) |
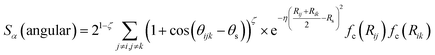 | (3) |
Modern machine learning frameworks provide automatic differentiation of tensor algebraic expressions, allowing a force field developer to obtain the gradient of a molecular potential 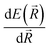 in a single line of code, once the expression for E(
in a single line of code, once the expression for E(![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) ) has been written. An important feature of our code is that this symmetry function is coded within the TensorFlow system,88 so all the parameters of this descriptor can be optimized alongside the network weights to minimize error. Our implementation of the symmetry function employs a list of nearest-pairs and triples within radial cutoffs such that the scaling of the overall network is asymptotically linear. On an ordinary laptop equipped with only a CPU, a force/energy call on 20
) has been written. An important feature of our code is that this symmetry function is coded within the TensorFlow system,88 so all the parameters of this descriptor can be optimized alongside the network weights to minimize error. Our implementation of the symmetry function employs a list of nearest-pairs and triples within radial cutoffs such that the scaling of the overall network is asymptotically linear. On an ordinary laptop equipped with only a CPU, a force/energy call on 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms takes less than a minute.
000 atoms takes less than a minute.
The second term of our energy expression is the damped-shifted force (DSF) Coulomb energy of Gezelter and coworkers.89 The charges are obtained from a sub-network which reproduces molecular dipole moments. Previous studies90,91 included electrostatic energy by training the networks to learn Hirshfeld charges. Our charge model enforces conservation of total charge by evenly spreading any required neutralizing charge over the entire molecule or unit cell. The damped-shifted force ensures the long range continuity and differentiability of the effective Coulomb potential with smooth cutoffs. We modify the DSF kernel at short range with an “elu” type non-linearity,92 such that the forces within the radius of the Behler–Parinello symmetry function smoothly approach zero, avoiding singularities and interference with the Behler–Parinello many-body potential. The range separation concept has a long history in chemistry whenever two models of a physical force have complementary cost or accuracy range advantages.84 The energy of the DSF kernel is expressed as:
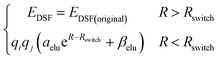 | (4) |
We employed a two step training approach. First, the charge networks are trained to learn the atom charges that predict the dipole moment. The loss function can be written as follows:
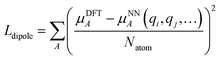 | (5) |
After the charge training is converged, we train the energy network. During the energy network training, the weights in charge networks are kept frozen, but they are still evaluated to calculate the electrostatic energy that is added to construct the total energy. Our Behler–Parinello many-body potential also absorbs the shape of the transition between the many-body and electrostatic regions. The learning target for the energy network includes both the DFT energy and DFT force. The loss function for the energy network training is:
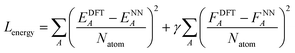 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 water clusters with 1 to 21 water molecules. The other network was trained on ∼3
000 water clusters with 1 to 21 water molecules. The other network was trained on ∼3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 different geometries of ∼15
000 different geometries of ∼15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 different molecules that only contain C, H, O and N and up to 35 atoms. Since these 15
000 different molecules that only contain C, H, O and N and up to 35 atoms. Since these 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules were sampled randomly from the Chemspider database, we will refer to this network as the “Chemspider network” in the following text. The training geometries were sampled with metadynamics93 and their energies calculated using the QChem94 program and ωB97X-D84 exchange correlation functional and a 6-311G** basis set.
000 molecules were sampled randomly from the Chemspider database, we will refer to this network as the “Chemspider network” in the following text. The training geometries were sampled with metadynamics93 and their energies calculated using the QChem94 program and ωB97X-D84 exchange correlation functional and a 6-311G** basis set.
Each charge network and energy network contains three fully-connected hidden layers with 500 hidden neurons in each layer. For the Chemspider network, a network with three hidden layers, with 2000 hidden neurons in each layer, is used for each charge network and energy network. L2 regularization is used for both networks and dropout95 on the last layer was used for the Chemspider network to prevent overfitting, with a dropout probability of 0.3. We chose a soft-plus function (ln(1.0 + eαx)/α) with α = 100 as the non-linear activation function and used the Adaptive moment solver (Adam)96 to fix the weights of the network. The test sets were separated from the training data by randomly choosing 20% of the molecules at the outset, which were kept independent throughout. Besides water, we will present calculations from molecules strictly absent from either the training or test set.
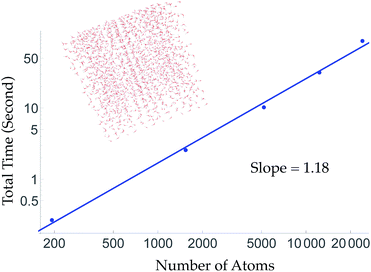
To obtain linear scaling, TensorMol uses atom neighbor lists within cutoffs. This allows double precision energy, charge and force calculations of up to 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms to be executed in less than 90 seconds on a 2015 Intel i7 2.5 GHz MacBook Pro (Fig. 2). Periodic evaluations are achieved by tessellation of a unit cell with summation of the energies of atoms within the cell. Periodic calculations require about three times more wall time to execute. Speedups greater than a factor of two are obtained automatically when using computers with GPUs (Fig. S7†) or single-precision calculations.
000 atoms to be executed in less than 90 seconds on a 2015 Intel i7 2.5 GHz MacBook Pro (Fig. 2). Periodic evaluations are achieved by tessellation of a unit cell with summation of the energies of atoms within the cell. Periodic calculations require about three times more wall time to execute. Speedups greater than a factor of two are obtained automatically when using computers with GPUs (Fig. S7†) or single-precision calculations.
3 Results
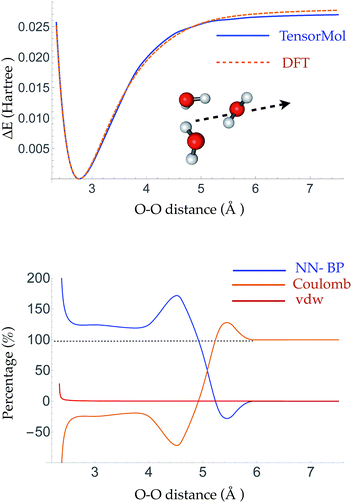
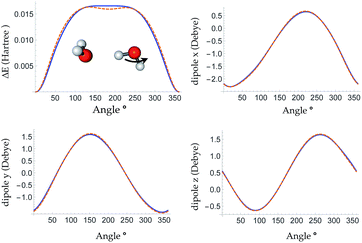
The root mean square error (RMSE) on the independent test set of the energy is 0.054 kcal mol−1 atom−1 and the RMSE of the force is 0.49 kcal mol−1 Å−1. The top panel of Fig. 3 is a plot of the potential energy surface (PES) of a water trimer when one of the water molecules is pulled away from the other two. One can see our neural network PES is not only in good agreement with the PES of the target method but is also smooth. To achieve this we use a variation of the soft-plus neuron rather than the rectified linear units that are popular in computer science. The latter train more efficiently, but produce discontinuous forces.The bottom panel shows the fractional contribution of each of the three energy components in eqn (1) to the binding energy along the trimer dissociation coordinate. At short range, most of the binding energy is contributed by the n-body neural network potential. When the distance between the monomer and the dimer approaches the cutoff distance of the neural network, the contribution of the neural network potential starts to decrease and the contribution of the electrostatic potential increases. After 6 Å, where the neural network symmetry functions on the atoms in the monomer have no contribution from the dimer, the neural network force drops smoothly to zero and the electrostatic interaction dominates. The small difference in the energy at 7 Å is due to the difference between the Madelung energy given by the learned charges, and the genuine physical cohesive forces at this distance. The dimer and monomer are beyond the symmetry function sensory radius, and so the charges are constant in this region. Future iterations of the charge network will use local-field information to improve this region of the PES. The learned inductive charges are of high quality considering their linear scaling cost. Fig. 4 shows the PES and dipole change of a water dimer when the hydrogen bond is broken by rotating the OH bond. Both the PES and dipole change fit well with the DFT results.
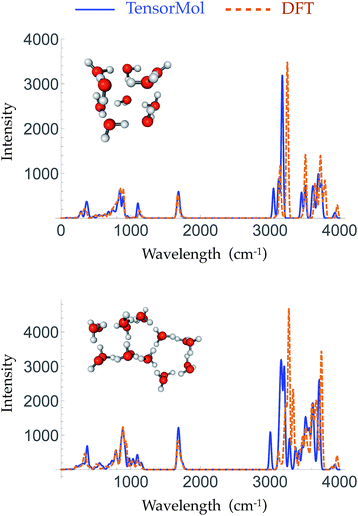
Given the increased dimensions of the Hessian, it is naturally a more stringent test to reproduce forces and infrared spectra than it is to simply produce energies. The top panel and bottom panel of Fig. 5 show the optimized geometries and IR spectra of a 10 water cluster and a 20 water cluster, respectively, generated using our force field and DFT. Each method uses its own equilibrium geometry, so this also tests the ability of TensorMol-0.1 to reproduce non-covalent geometries. Our force field quantitatively reproduces the IR spectra generated using DFT, both in terms of frequencies and intensities, especially for the water bend modes and inter-monomer modes. The Mean Absolute Error (MAE) of the frequencies in those two regions is 33.2 cm−1 for the 10 water cluster and 16.2 cm−1 for the 20 water cluster. The error is slightly larger in the water OH stretching region with a MAE of 34.2 cm−1 and 13.1 cm−1 for the 10 and 20 water clusters, respectively. This accuracy is comparable to high quality polarizable water force fields.6
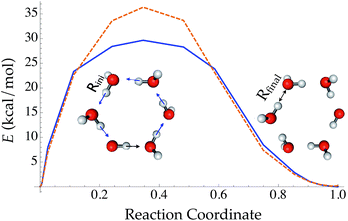
Compared with traditional force fields, one major advantage of TensorMol is its reactivity. TensorMol is able to simulate a concerted proton transfer in a water hexamer, finding a minimum energy transition path. The PES calculated using a nudged elastic band (NEB) method97 with the TensorMol force field and the PES calculated using DFT are shown in Fig. 6. The barrier height predicted by TensorMol is 29.7 kcal mol−1, which is 6.7 kcal mol−1 lower than the prediction from DFT, which is remarkable considering the dearth of transition structures in the training data. Our method of sampling molecular geometries uses a meta-dynamics procedure described elsewhere,93 so these proton transfers do occur in the training data although extremely infrequently.
Encouraged by our results from studying water, we developed a force field with applicability across the chemical space spanned by C, N, O and H. The Chemspider dataset that we used to train our force field covers a vast area of chemical space containing 15 thousand different molecules and 3 million geometries. The geometries are generated using a meta-dynamics procedure,98 which ensures that each new geometry is a fresh part of chemical space; energies up to 400kbT are sampled in the data. We describe the details of this meta-dynamics sampling algorithm, which we have found vital to achieving robust and transferable force fields elsewhere.93 The diversity of structures makes learning the Chemspider dataset a much harder task for the TensorMol-0.1 network; the test set RMSE of energy is 0.24 kcal mol−1 atom−1 and the RMSE of force is 2.4 kcal mol−1 atom−1. More importantly, the model usefully reproduces several elements of molecular structures, at and away from equilibrium, for molecules outside its training set. It robustly optimizes the geometries of typical organic molecules to structures that match DFT well, and yields infrared frequencies and intensities that are in good agreement with ab initio calculations. It is a black-box method that does not rely on any specific atom type, connectivity, etc., which one would need to specify in a traditional classical force field. The few proteins we have examined remain stable and near their experimental structures when optimized or propagated at room temperature using the TensorMol-0.1 force field.
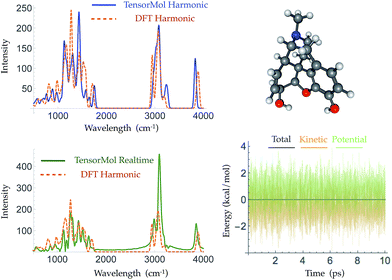
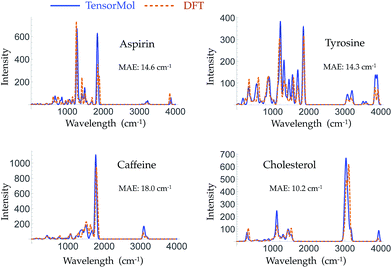
Morphine was not included in our training set. The top right panel of Fig. 7 shows the geometry of morphine that is optimized with our force field. The RMSE of the bond lengths predicted by our force field is 0.0067 Å and the RMSE of the angles is 1.04 degrees, compared with the source DFT model chemistry. The upper left panel plots the harmonic IR spectra generated using DFT and the TensorMol force field, at their respective optimized geometries. One can see the IR spectrum generated using our force field is in good agreement with the DFT-generated IR spectrum. The MAE in our force field frequencies is 13.7 cm−1 compared with the DFT frequencies, which is about half of the MAE in the prediction using MMFF9499 (Fig. S3†). Fig. 8 shows comparisons of the IR spectra that are generated using these two methods for aspirin, typrosine, caffeine and cholesterol. All four of these molecules were not included in the training set. The MAE in the frequencies predicted by our field is less than 20 cm−1 for all four molecules, compared with the target DFT frequencies. As Fig. S4† shows, the MAE in the frequencies calculated using MMFF94 are 2 to 3 times larger than the MAE in the frequencies calculated using our force field for these four molecules. The intensities calculated using MMFF94 are also qualitatively different to the DFT intensities. The concept of a chemical bond and force constant are not enforced in any way, yet good agreement with DFT is obtained at a tiny fraction of the original cost.
Traditional harmonic vibrational spectra require quadratic computational effort, which works against the speed advantage of a NNMC. For large systems, one can use the molecular dynamics functionality of TensorMol to simulate infrared spectra, Fourier transforming the dipole–dipole correlation function of conservative Newtonian dynamics, whose cost grows linearly with the size of the system. The lower left panel of Fig. 7 shows the infrared spectrum produced by propagation in TensorMol-0.1, also showcasing the good energy conservation of TensorMol. Unlike when using a traditional force field, in this case it is non-trivial to obtain smoothly differentiable NNMCs. 64-bit precision needs to be used as the network cannot be made too flexible, and smooth versions of the typical rectified linear units need to be used. Our package can be used in this way to simulate IR spectra of large systems with linear cost.
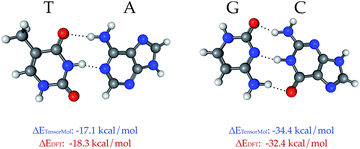
TensorMol-0.1 uses a relatively simple treatment of the electrostatic and van der Waals forces, which we would like to augment in the future with a many-body dispersion scheme.100 However, a main advantage of the approach used by TensorMol-0.1 is that no self-consistent polarization equation is solved even though the charges are inductive, which results in linear scaling and ease of inexpensively calculating the electrostatic energies of even very large molecules. At shorter ranges, non-covalent interactions like hydrogen bonds are dealt with by the Behler–Parinello portion of the network. The Chemspider training data include some examples of dimers and intra-molecular hydrogen bonds. To our surprise, the treatment of the inter-molecular interactions that were not targets for TensorMol-0.1 are satisfactory. Fig. 9 shows the optimized geometries and binding energies of two DNA base pairs calculated using our force field. The target DFT method predicts a binding energy of 18.3 kcal mol−1 for the thymine–adenine (TA) pair and a binding energy of 32.4 kcal mol−1 for the guanine–cytosine (GC) pair. The prediction using our force field is 1.2 kcal mol−1 smaller for the TA pair and 2.0 kcal mol−1 larger for the GC pair relative to DFT.
One holy grail in the field of neural network model chemistries is to simulate biological chemistry without QM-MM or bespoke force fields. Protein simulation also demonstrates several important features of neural network model chemistry: reasonable inter-molecular forces, stability, scalability and generalization far from small-molecule training data. TensorMol-0.1 was not trained on any peptide polymers and includes no biological data of any sort. To our pleasant surprise, even this first iteration of neural network model chemistry is accurate enough to perform rudimentary studies on small proteins. Fig. 10 shows geometries sampled from a 1 picosecond, periodic, 300 K TensorMol dynamics NVT trajectory in explicit solvent. The initial structure (included in the supplementary information) was generated from the PDB structure 2MZX using OpenMM’s automatic solvation and hydrogenation scripts,101 but includes nothing but atom coordinates. This short alpha-helix is stable, both in optimizations and dynamics, and the structures sampled during the dynamics simulation superficially resemble the solution NMR structure. Traditional force fields will always be less expensive (by some prefactor) than NNMCs, yet the reactivity advantages of NNMCs and the ease of set up will probably lead to a rapid adoption of these methods in the biological community.
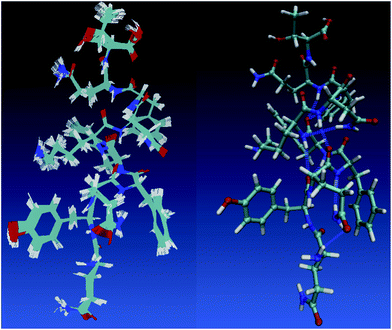 | ||
| Fig. 10 The left panel shows samples from a 1 picosecond NVT (Nosé) trajectory of solvated 2MZX at 300 K, simulated by our TensorMol force field in explicit water. The right panel is the NMR structure of 2MZX from the PDB database. | ||
4 Discussion and conclusions
We have presented a transferable neural network model chemistry, TensorMol-0.1, with long-range coulombic physics and a short-range n-body potential. The model is integrated in an open-source Python package, which provides many of the types of simulation commonly used in chemistry. The method can be used to scan conformational and chemical space along the singlet neutral potential energy surface with high throughput using bare atomic coordinates.TensorMol-0.1 is not the final iteration of a neural network model chemistry, although it shows that DFT-quality predictions can be made by models with five orders of magnitude lower cost. Inexpensive post-DFT corrections such as many-body dispersion100 will become even more powerful when integrated with these potentials, opening the door to quantitative treatments of large systems. NNMCs may compete strongly with DFT packages, and provide an interesting complement to QM-MM-type simulations in the near future.
There are several clear paths to extend this work:
• generalize the descriptors to encode other physical atom properties besides charge (spin or polarizability)
• develop accurate descriptors whose cost grows linearly with the number of elements treated
• extend the range of the n-body embedding
• explore the hierarchy of physical detail between force fields and semi-empirical electronic structures
These are the directions of continuing study in our group and others.
Conflicts of interest
There are no conflicts to declare.References
- A. Lopez-Bezanilla and O. A. von Lilienfeld, Phys. Rev. B, 2014, 89, 235411 CrossRef.
- G. Pilania, C. Wang, X. Jiang, S. Rajasekaran and R. Ramprasad, Sci. Rep., 2013, 3, 2810 CrossRef PubMed.
- K. Schütt, H. Glawe, F. Brockherde, A. Sanna, K. Müller and E. Gross, Phys. Rev. B, 2014, 89, 205118 CrossRef.
- A. P. Bartok, M. C. Payne, R. Kondor and G. Csanyi, Phys. Rev. Lett., 2010, 104, 136403 CrossRef PubMed.
- I. Kruglov, O. Sergeev, A. Yanilkin and A. R. Oganov, Sci. Rep., 2017, 7, 8512 CrossRef PubMed.
- G. R. Medders, A. W. Götz, M. A. Morales, P. Bajaj and F. Paesani, J. Chem. Phys., 2015, 143, 104102 CrossRef PubMed.
- G. R. Medders, V. Babin and F. Paesani, J. Chem. Theory Comput., 2013, 9, 1103–1114 CrossRef CAS PubMed.
- S. K. Reddy, S. C. Straight, P. Bajaj, C. Huy Pham, M. Riera, D. R. Moberg, M. A. Morales, C. Knight, A. W. Götz and F. Paesani, J. Chem. Phys., 2016, 145, 194504 CrossRef PubMed.
- M. Riera, N. Mardirossian, P. Bajaj, A. W. Götz and F. Paesani, J. Chem. Phys., 2017, 147, 161715 CrossRef PubMed.
- D. R. Moberg, S. C. Straight, C. Knight and F. Paesani, J. Phys. Chem. Lett., 2017, 8(12), 2579–2583 CrossRef CAS PubMed.
- S. T. John and G. Csanyi, J. Phys. Chem. B, 2017, 121(48), 10934–10949 CrossRef CAS PubMed.
- S. Chmiela, A. Tkatchenko, H. E. Sauceda, I. Poltavsky, K. T. Schütt and K.-R. Müller, Sci. Adv., 2017, 3, e1603015 CrossRef PubMed.
- L. Mones, N. Bernstein and G. Csanyi, J. Chem. Theory Comput., 2016, 12, 5100–5110 CrossRef CAS PubMed.
- K. Yao and J. Parkhill, J. Chem. Theory Comput., 2016, 12, 1139–1147 CrossRef CAS PubMed.
- J. C. Snyder, M. Rupp, K. Hansen, L. Blooston, K.-R. Müller and K. Burke, J. Chem. Phys., 2013, 139, 224104 CrossRef PubMed.
- F. Brockherde, L. Vogt, L. Li, M. E. Tuckerman, K. Burke and K.-R. Müller, Nat. Commun., 2017, 8, 872 CrossRef PubMed.
- J. C. Snyder, M. Rupp, K. Hansen, K.-R. Müller and K. Burke, Phys. Rev. Lett., 2012, 108, 253002 CrossRef PubMed.
- L. Li, J. C. Snyder, I. M. Pelaschier, J. Huang, U.-N. Niranjan, P. Duncan, M. Rupp, K.-R. Müller and K. Burke, Int. J. Quantum Chem., 2016, 116, 819–833 CrossRef CAS.
- L. Li, T. E. Baker, S. R. White and K. Burke, et al. , Phys. Rev. B, 2016, 94, 245129 CrossRef.
- K. Vu, J. C. Snyder, L. Li, M. Rupp, B. F. Chen, T. Khelif, K.-R. Müller and K. Burke, Int. J. Quantum Chem., 2015, 115, 1115–1128 CrossRef CAS.
- R. T. McGibbon, A. G. Taube, A. G. Donchev, K. Siva, F. Hernández, C. Hargus, K.-H. Law, J. L. Klepeis and D. E. Shaw, J. Chem. Phys., 2017, 147, 161725 CrossRef PubMed.
- J. Wu, L. Shen and W. Yang, J. Chem. Phys., 2017, 147, 161732 CrossRef PubMed.
- F. Fracchia, G. Del Frate, G. Mancini, W. Rocchia and V. Barone, J. Chem. Theory Comput., 2018, 14(1), 255–273 CrossRef CAS PubMed.
- Y. Li, H. Li, F. C. Pickard IV, B. Narayanan, F. G. Sen, M. K. Chan, S. K. Sankaranarayanan, B. R. Brooks and B. Roux, J. Chem. Theory Comput., 2017, 13, 4492–4503 CrossRef CAS PubMed.
- M. Rupp, A. Tkatchenko, K.-R. Müller and O. A. Von Lilienfeld, Phys. Rev. Lett., 2012, 108, 058301 CrossRef PubMed.
- K. Hansen, F. Biegler, R. Ramakrishnan, W. Pronobis, O. A. Von Lilienfeld, K.-R. Müller and A. Tkatchenko, J. Phys. Chem. Lett., 2015, 6, 2326–2331 CrossRef CAS PubMed.
- Y. T. Sun, H. Bai, M.-Z. Li and W. Wang, J. Phys. Chem. Lett., 2017, 8, 3434–3439 CrossRef CAS PubMed.
- R. Jinnouchi and R. Asahi, J. Phys. Chem. Lett., 2017, 8, 4279–4283 CrossRef CAS PubMed.
- L. M. Ghiringhelli, J. Vybiral, E. Ahmetcik, R. Ouyang, S. V. Levchenko, C. Draxl and M. Scheffler, New J. Phys., 2017, 19, 023017 CrossRef.
- R. Ouyang, S. Curtarolo, E. Ahmetcik, M. Scheffler and L. M. Ghiringhelli, arXiv preprint arXiv:1710.03319, 2017.
- O. Isayev, C. Oses, C. Toher, E. Gossett, S. Curtarolo and A. Tropsha, Nat. Commun., 2017, 8, 15679 CrossRef CAS PubMed.
- A. Grisafi, D. M. Wilkins, G. Csanyi and M. Ceriotti, arXiv preprint arXiv:1709.06757, 2017.
- E. Kim, K. Huang, A. Tomala, S. Matthews, E. Strubell, A. Saunders, A. McCallum and E. Olivetti, Sci. Data, 2017, 4, 170127 CrossRef CAS PubMed.
- J. Hachmann, R. Olivares-Amaya, S. Atahan-Evrenk, C. Amador-Bedolla, R. S. Sánchez-Carrera, A. Gold-Parker, L. Vogt, A. M. Brockway and A. Aspuru-Guzik, J. Phys. Chem. Lett., 2011, 2, 2241–2251 CrossRef CAS.
- J. Hachmann, R. Olivares-Amaya, A. Jinich, A. L. Appleton, M. A. Blood-Forsythe, L. R. Seress, C. Roman-Salgado, K. Trepte, S. Atahan-Evrenk and S. Er, Energy Environ. Sci., 2014, 7, 698–704 CAS.
- O. Isayev, D. Fourches, E. N. Muratov, C. Oses, K. Rasch, A. Tropsha and S. Curtarolo, Chem. Mater., 2015, 27, 735–743 CrossRef CAS.
- R. Olivares-Amaya, C. Amador-Bedolla, J. Hachmann, S. Atahan-Evrenk, R. S. Sánchez-Carrera, L. Vogt and A. Aspuru-Guzik, Energy Environ. Sci., 2011, 4, 4849–4861 CAS.
- Z. W. Ulissi, M. T. Tang, J. Xiao, X. Liu, D. A. Torelli, M. Karamad, K. Cummins, C. Hahn, N. S. Lewis and T. F. Jaramillo, et al. , ACS Catal., 2017, 7, 6600–6608 CrossRef CAS.
- C. M. Handley and P. L. Popelier, J. Phys. Chem. A, 2010, 114, 3371–3383 CrossRef CAS PubMed.
- J.-P. Piquemal and K. D. Jordan, J. Chem. Phys., 2017, 147, 161401 CrossRef PubMed.
- K. Mills, M. Spanner and I. Tamblyn, Phys. Rev.A, 2017, 96, 042113 CrossRef.
- M. Malshe, L. Raff, M. Hagan, S. Bukkapatnam and R. Komanduri, J. Chem. Phys., 2010, 132, 204103 CrossRef CAS PubMed.
- A. A. Peterson, J. Chem. Phys., 2016, 145, 074106 CrossRef PubMed.
- E. D. Cubuk, B. D. Malone, B. Onat, A. Waterland and E. Kaxiras, J. Chem. Phys., 2017, 147, 024104 CrossRef PubMed.
- B. K. Carpenter, G. S. Ezra, S. C. Farantos, Z. C. Kramer and S. Wiggins, J. Phys. Chem. B, 2017 DOI:10.1021/acs.jpcb.7b08707.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- J. Behler, Phys. Chem. Chem. Phys., 2011, 13, 17930–17955 RSC.
- K. Shakouri, J. Behler, J. Meyer and G.-J. Kroes, J. Phys. Chem. Lett., 2017, 8, 2131–2136 CrossRef CAS PubMed.
- J. Behler, Angew. Chem., Int. Ed., 2017, 56, 12828–12840 CrossRef CAS PubMed.
- J. Han, L. Zhang, R. Car and W. E, Comm Comput Phys, 2018, 23, 629–639 Search PubMed.
- R. Z. Khaliullin, H. Eshet, T. D. Kühne, J. Behler and M. Parrinello, Nat. Mater., 2011, 10, 693–697 CrossRef CAS PubMed.
- M. Gastegger, J. Behler and P. Marquetand, Chem. Sci., 2017, 8, 6924–6935 RSC.
- R. Kobayashi, D. Giofré, T. Junge, M. Ceriotti and W. A. Curtin, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 1, 053604 Search PubMed.
- K. Yao, J. E. Herr, S. N. Brown and J. Parkhill, J. Phys. Chem. Lett., 2017, 8(12), 2689–2694 CrossRef CAS PubMed.
- B. Kolb, L. C. Lentz and A. M. Kolpak, Sci. Rep., 2017, 7, 1192 CrossRef PubMed.
- N. Lubbers, J. S. Smith and K. Barros, arXiv preprint arXiv:1710.00017, 2017.
- A. Khorshidi and A. A. Peterson, Comput. Phys. Commun., 2016, 207, 310–324 CrossRef CAS.
- K. Yao, J. E. Herr and J. Parkhill, J. Chem. Phys., 2017, 146, 014106 CrossRef PubMed.
- S. Manzhos, R. Dawes and T. Carrington, Int. J. Quantum Chem., 2015, 115, 1012–1020 CrossRef CAS.
- S. Manzhos, K. Yamashita and T. Carrington Jr, Comput. Phys. Commun., 2009, 180, 2002–2012 CrossRef CAS.
- K. Shao, J. Chen, Z. Zhao and D. H. Zhang, J. Chem. Phys., 2016, 145, 071101 CrossRef PubMed.
- Z. Zhang and D. H. Zhang, J. Chem. Phys., 2014, 141, 144309 CrossRef PubMed.
- J. Li, J. Chen, Z. Zhao, D. Xie, D. H. Zhang and H. Guo, J. Chem. Phys., 2015, 142, 204302 CrossRef PubMed.
- R. Conte, C. Qu and J. M. Bowman, J. Chem. Theory Comput., 2015, 11, 1631–1638 CrossRef CAS PubMed.
- X. Ma, Z. Li, L. E. Achenie and H. Xin, J. Phys. Chem. Lett., 2015, 6, 3528–3533 CrossRef CAS PubMed.
- J. P. Janet and H. J. Kulik, Chem. Sci., 2017, 8, 5137–5152 RSC.
- J. P. Janet and H. J. Kulik, J. Phys. Chem. A, 2017, 121(46), 8939–8954 CrossRef CAS PubMed.
- F. Häse, C. Kreisbeck and A. Aspuru-Guzik, Chem. Sci., 2017, 8, 8419–8426 RSC.
- T. Bereau, R. A. DiStasio Jr, A. Tkatchenko and O. A. von Lilienfeld, arXiv preprint arXiv:1710.05871, 2017.
- F. A. Faber, L. Hutchison, B. Huang, J. Gilmer, S. S. Schoenholz, G. E. Dahl, O. Vinyals, S. Kearnes, P. F. Riley and O. A. von Lilienfeld, J. Chem. Theory Comput., 2017, 13(11), 5255–5264 CrossRef CAS PubMed.
- K. T. Schütt, F. Arbabzadah, S. Chmiela, K. R. Müller and A. Tkatchenko, Nat. Commun., 2017, 8, 13890 CrossRef PubMed.
- X.-X. Zhou, W.-F. Zeng, H. Chi, C. Luo, C. Liu, J. Zhan, S.-M. He and Z. Zhang, Anal. Chem., 2017, 89(23), 12690–12697 CrossRef CAS PubMed.
- J. Timoshenko, D. Lu, Y. Lin and A. I. Frenkel, J. Phys. Chem. Lett., 2017, 8(20), 5091–5098 CrossRef PubMed.
- J. Li, D. Cai and X. He, arXiv preprint arXiv:1709.03741, 2017.
- B. Ramsundar, B. Liu, Z. Wu, A. Verras, M. Tudor, R. P. Sheridan and V. Pande, J. Chem. Inf. Model., 2017, 57, 2068–2076 CrossRef CAS PubMed.
- M. Segler, M. Preuß and M. P. Waller, arXiv preprint arXiv:1702.00020, 2017.
- G. L. Guimaraes, B. Sanchez-Lengeling, P. L. C. Farias and A. Aspuru-Guzik, arXiv preprint arXiv:1705.10843, 2017.
- J. N. Wei, D. Duvenaud and A. Aspuru-Guzik, ACS Cent. Sci., 2016, 2, 725–732 CrossRef CAS PubMed.
- R. Gómez-Bombarelli, D. Duvenaud, J. M. Hernández-Lobato, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, arXiv preprint arXiv:1610.02415, 2016.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- B. T. Thole, Chem. Phys., 1981, 59, 341–350 CrossRef CAS.
- J. S. Smith, O. Isayev and A. E. Roitberg, Chem. Sci., 2017, 8, 3192–3203 RSC.
- J. S. Smith, O. Isayev and A. E. Roitberg, Sci. Data, 2017, 4, 170193 CrossRef CAS PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- M. Ceriotti, J. More and D. E. Manolopoulos, Comput. Phys. Commun., 2014, 185, 1019–1026 CrossRef CAS.
- V. L. Deringer and G. Csanyi, Phys. Rev. B, 2017, 95, 094203 CrossRef.
- T. Morawietz and J. Behler, J. Phys. Chem. A, 2013, 117, 7356–7366 CrossRef CAS PubMed.
- M. Abadi, A. Agarwal, P. Barham, E. Brevdo, Z. Chen, C. Citro, G. S. Corrado, A. Davis, J. Dean, M. Devin, S. Ghemawat, I. Goodfellow, A. Harp, G. Irving, M. Isard, Y. Jia, R. Jozefowicz, L. Kaiser, M. Kudlur, J. Levenberg, D. Mané, R. Monga, S. Moore, D. Murray, C. Olah, M. Schuster, J. Shlens, B. Steiner, I. Sutskever, K. Talwar, P. Tucker, V. Vanhoucke, V. Vasudevan, F. Viégas, O. Vinyals, P. Warden, M. Wattenberg, M. Wicke, Y. Yu and X. Zheng, TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems, 2015, http://tensorflow.org/ Search PubMed.
- C. J. Fennell and J. D. Gezelter, J. Chem. Phys., 2006, 124, 234104 CrossRef PubMed.
- T. Morawietz, V. Sharma and J. Behler, J. Chem. Phys., 2012, 136, 064103 CrossRef PubMed.
- N. Artrith, T. Morawietz and J. Behler, Phys. Rev. B, 2011, 83, 153101 CrossRef.
- D.-A. Clevert, T. Unterthiner and S. Hochreiter, arXiv preprint arXiv:1511.07289, 2015.
- J. E. Herr, K. Yao, R. McIntyre, D. Toth and J. Parkhill, arXiv preprint arXiv:1712.07240, 2017.
- Y. Shao, Z. Gan, E. Epifanovsky, A. T. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng and X. Feng, et al. , Mol. Phys., 2015, 113, 184–215 CrossRef CAS.
- N. Srivastava, G. E. Hinton, A. Krizhevsky, I. Sutskever and R. Salakhutdinov, J. Mach. Learn. Res., 2014, 15, 1929–1958 Search PubMed.
- D. Kingma and J. Ba, arXiv preprint arXiv:1412.6980, 2014.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- A. Barducci, G. Bussi and M. Parrinello, Phys. Rev. Lett., 2008, 100, 020603 CrossRef PubMed.
- T. A. Halgren, J. Comput. Chem., 1996, 17, 553–586 CrossRef CAS.
- A. Tkatchenko, R. A. DiStasio Jr, R. Car and M. Scheffler, Phys. Rev. Lett., 2012, 108, 236402 CrossRef PubMed.
- P. Eastman, J. Swails, J. D. Chodera, R. T. McGibbon, Y. Zhao, K. A. Beauchamp, L.-P. Wang, A. C. Simmonett, M. P. Harrigan, C. D. Stern, R. P. Wiewiora, B. R. Brooks and V. S. Pande, PLoS Comput. Biol., 2017, 13, 1–17 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7sc04934j |
| This journal is © The Royal Society of Chemistry 2018 |