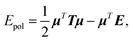Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Tinker-HP: a massively parallel molecular dynamics package for multiscale simulations of large complex systems with advanced point dipole polarizable force fields†
Louis
Lagardère
abc,
Luc-Henri
Jolly
b,
Filippo
Lipparini
 d,
Félix
Aviat
c,
Benjamin
Stamm
d,
Félix
Aviat
c,
Benjamin
Stamm
 e,
Zhifeng F.
Jing
e,
Zhifeng F.
Jing
 f,
Matthew
Harger
f,
Hedieh
Torabifard
g,
G. Andrés
Cisneros
f,
Matthew
Harger
f,
Hedieh
Torabifard
g,
G. Andrés
Cisneros
 h,
Michael J.
Schnieders
i,
Nohad
Gresh
c,
Yvon
Maday
jkl,
Pengyu Y.
Ren
f,
Jay W.
Ponder
h,
Michael J.
Schnieders
i,
Nohad
Gresh
c,
Yvon
Maday
jkl,
Pengyu Y.
Ren
f,
Jay W.
Ponder
 m and
Jean-Philip
Piquemal
m and
Jean-Philip
Piquemal
 *cfk
*cfk
aSorbonne Université, Institut des Sciences du Calcul et des Données, Paris, France
bSorbonne Université, Institut Parisien de Chimie Physique et Théorique, CNRS, FR 2622, Paris, France
cSorbonne Université, Laboratoire de Chimie Théorique, UMR 7616, CNRS, Paris, France. E-mail: jpp@lct.jussieu.fr
dUniversita di Pisa, Dipartimento di Chimica e Chimica Industriale, Pisa, Italy
eMATHCCES, Department of Mathematics, RWTH Aachen University, Aachen, Germany
fThe University of Texas at Austin, Department of Biomedical Engineering, TX, USA
gDepartment of Chemistry, Wayne State University, Detroit, MI 48202, USA
hDepartment of Chemistry, University of North Texas, Denton, TX 76202, USA
iThe University of Iowa, Department of Biomedical Engineering, Iowa City, IA, USA
jSorbonne Université, Laboratoire Jacques-Louis Lions, UMR 7598, CNRS, Paris, France
kInstitut Universitaire de France, Paris, France
lBrown University, Division of Applied Maths, Providence, RI, USA
mWashington University in Saint Louis, Department of Chemistry, Saint Louis, MI, USA
First published on 27th November 2017
Abstract
We present Tinker-HP, a massively MPI parallel package dedicated to classical molecular dynamics (MD) and to multiscale simulations, using advanced polarizable force fields (PFF) encompassing distributed multipoles electrostatics. Tinker-HP is an evolution of the popular Tinker package code that conserves its simplicity of use and its reference double precision implementation for CPUs. Grounded on interdisciplinary efforts with applied mathematics, Tinker-HP allows for long polarizable MD simulations on large systems up to millions of atoms. We detail in the paper the newly developed extension of massively parallel 3D spatial decomposition to point dipole polarizable models as well as their coupling to efficient Krylov iterative and non-iterative polarization solvers. The design of the code allows the use of various computer systems ranging from laboratory workstations to modern petascale supercomputers with thousands of cores. Tinker-HP proposes therefore the first high-performance scalable CPU computing environment for the development of next generation point dipole PFFs and for production simulations. Strategies linking Tinker-HP to Quantum Mechanics (QM) in the framework of multiscale polarizable self-consistent QM/MD simulations are also provided. The possibilities, performances and scalability of the software are demonstrated via benchmarks calculations using the polarizable AMOEBA force field on systems ranging from large water boxes of increasing size and ionic liquids to (very) large biosystems encompassing several proteins as well as the complete satellite tobacco mosaic virus and ribosome structures. For small systems, Tinker-HP appears to be competitive with the Tinker-OpenMM GPU implementation of Tinker. As the system size grows, Tinker-HP remains operational thanks to its access to distributed memory and takes advantage of its new algorithmic enabling for stable long timescale polarizable simulations. Overall, a several thousand-fold acceleration over a single-core computation is observed for the largest systems. The extension of the present CPU implementation of Tinker-HP to other computational platforms is discussed.
1 Introduction
Over the last 60 years, classical Molecular Dynamics (MD) has been an intense field of research with a high rate growth. Indeed, solving Newton equations of motion to resolve the time-dependent dynamics of atoms within large molecules allows to perform simulations in various fields of research ranging from materials to biophysics and chemistry. For example, in the community of protein simulations, classical force fields (FF) such as CHARMM,1 AMBER,2 OPLS,3 GROMOS4 and others,5 enabled large scale simulations on complex systems thanks to the low computational cost of their energy function. In that context, various simulation packages appeared, often associated to these FF such as the popular CHARMM,6 GROMOS7 and AMBER softwares.8 Among these, Tinker (presently version 8 (ref. 9)) was introduced in 1990 with the philosophy of being both user friendly and to provide a reference toolbox for developers. Later on, the evolution of computer systems enabled the emergence of massively parallel softwares dedicated to molecular simulations such as LAMMPS,10 NAMD,11 Gromacs,12 AMBER (PME-MD),13 DLPOLY,14 Genesis15 or Desmond.16 As they were granted the use of large computational resources, access to million atoms systems and biological time scales became possible.17 Nevertheless, up to now, such simulations are mainly limited to first-generation molecular mechanics (MM) models that remains confined to a lower resolution approximation of the true quantum mechanical Born–Oppenheimer potential energy surfaces (PES). However, beside these methods, more advanced second generation “polarizable” force fields (PFF) emerged in the last 30 years.18–28 Grounded on Quantum Mechanics (QM) and usually calibrated on the basis of Energy Decomposition Analysis (EDA),29 they go beyond pairwise approximation by including explicit many-body induction effects such as polarization and in some cases charge-transfer. Fluctuating charges, classical Drude approaches or point dipole coupled to point-charge models using distributed polarizabilities are among the most studied techniques aiming to include polarization effects.28 On the accuracy side, some PFF go beyond the point charge approximation incorporating a more detailed representation of the permanent and induced charge distributions using QM-derived distributed multipoles and polarizabilities.18,19,24,26 Recently, a third-generation PFF using distributed frozen electronic densities in order to incorporate short-range quantum effects30 appeared. In term of PES, these advanced force fields clearly tend to offer improved accuracy, better transferability and therefore are hoped to be more predictive. Unfortunately, everything has a cost: such elegant methods are more complex by design, and are therefore computationally challenging. Until recently the more advanced point dipole polarizable approaches were thought to be doomed for the simulation of realistic systems due to the evaluation cost of the polarization energy. Large scale polarizable production MD simulations were limited to the use of the Drude-type/point-charge model (using an extended Lagrangian propagation scheme)31 that was found to be more tractable than point dipole models (using iterative solvers) coupled to multipolar representation of the permanent charge distribution. Nevertheless, despite this scalability issue, time was not lost and accurate models were developed such as the Tinker package, original home of the multipolar AMOEBA PFF,24 specialized in offering a dedicated development platform with all required advanced algorithms for these accurate techniques. Moreover, ten years ago, a hardware technical revolution in the field of High Performance Computing (HPC), had a profound impact on MD simulations with classical FF.32 Indeed, the introduction of Graphical Processing Units (GPUs) offered a brute force hardware acceleration to MD packages thanks to simple- or mixed-precision implementations.33 Tinker benefited from the availability of this low cost but powerful type of hardware. It led to a GPU version of the code denoted Tinker-OpenMM.34 The code is based both on Tinker and on the OpenMM library (now version 7 (ref. 35)) which pioneered the use of GPUs with polarizable force fields. Tinker-OpenMM offers a 200-fold acceleration compared to a regular single core CPU computation giving access to accurate free energy simulations. However, when one considers the need for biophysical simulations, this acceleration remains not sufficient.The purpose of the present work is to push the scalability improvements of Tinker through new algorithms to explore strategies enabling a 1000-fold and more speedup. These new developments aim towards modern “big Iron” petascale supercomputers using distributed memory and the code design also offers consequent speedups on laboratory clusters and on multicore desktop stations. The philosophy here is to build a highly scalable double precision code, fully compatible and consistent with the canonical reference Tinker and Tinker-OpenMM codes. As the new code remains a part of the Tinker package, it is designed to keep its user-friendliness offered to both developers and users but also to provide an extended access to larger scale/longer timescale MD simulations on any type of CPU platforms. The incentive to produce such a reference double precision code is guided by the will to also perform scalable hybrid QM/MM MD simulations where rounding errors must be eliminated. This will bring us not to cut any corners in our numerical implementation with the key mantra that one should not scale at any cost, as the algorithms developed in this interdisciplinary project should be based on solid mathematical grounds.
The paper is organized as follows. First, we will present the newly developed extension of 3D spatial decomposition and memory distribution to polarizable point dipole models that is at the heart of Tinker-HP for short-range interactions. Then we will detail the handling of long-range electrostatic and polarization interactions with a new framework coupling Smooth Particle Ewald to Krylov iterative and non iterative polarization solvers. We will then introduce the possibilities of the software and show benchmarks for selected applications in the context of the AMOEBA PFF.24,36 Finally, we will present functionalities of Tinker-HP that go beyond MD simulations in periodic boundary conditions as we conclude by drawing some perspectives about evolutions of the code towards next HPC platforms.
2 Accelerating polarizable molecular dynamics using massively parallel 3D spatial decomposition
In this section, we describe the first extension of 3D spatial decomposition to polarizable point dipoles models dedicated to production simulations. Indeed, in the past, point dipole model implementations in parallel have been limited to the use of a few dozen processors.37 In this section, we detail the parallelization strategy used in Tinker-HP to overcome this problem and to deal with local interactions, including the direct-space part of electrostatic and polarization interactions. The long-range, reciprocal field part of such interactions, is discussed in Section 3.2.1 State of the art in massively parallel implementation of classical molecular dynamics simulations
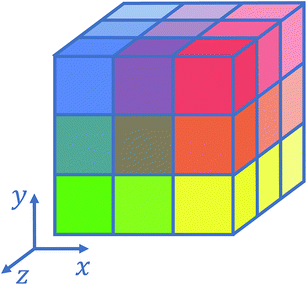
Several strategies10–12,16 have been devised in order to treat short-range interactions on large-scale parallel computers using distributed memory parallelism. In Tinker-HP, we have implemented a spatial decomposition (or domain decomposition) method. In this approach, the simulation domain is decomposed in 3D blocks and each block is assigned to a processor. Each processor then handles the computation of the forces and the update of the coordinates for the atoms assigned to the block at each time-step. This strategy is motivated by the fact that the interactions considered are short-range, and that the positions of the atoms do not change much between two consecutive time-steps. An example of such a decomposition with 3 × 3 × 3 = 27 blocks is given in Fig. 1. One can show10 that if the cutoff (rc) involved in the short-range interactions is superior to the size of an edge of a block, which is the case with a high number of processors, the amount of data to be communicated in and out of each processor at each time step (the so-called communication volume) scales like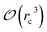 (if the density of the system is uniform) independently of the number of processors. As a consequence, the communications are local which is an advantage of this method over the other ones. However, achieving a good load-balancing is harder using this strategy when the density of the system is not uniform or when the simulation box is not a parallelepiped.
(if the density of the system is uniform) independently of the number of processors. As a consequence, the communications are local which is an advantage of this method over the other ones. However, achieving a good load-balancing is harder using this strategy when the density of the system is not uniform or when the simulation box is not a parallelepiped.
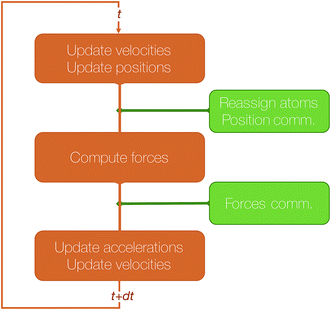
Let us give more details about the algorithm and the main steps required to perform a time step of MD using this method. We assume that the simulated system resides in a box that has been divided in as many 3D blocks as the number of processors used. Let us focus on a processor that has been assigned a 3D block and let us assume that this processor knows the current positions, velocities and accelerations of the atoms currently belonging to this block. In integrator schemes such as velocity Verlet, the first integration step consists of an update of the local positions and a first update of the velocities. Because of these position changes, some atoms may cross the local block boundaries and need to be reassigned to neighboring blocks. This step, that we will call “reassign step” only requires local communications between a small number of neighboring processes.
In the second step, the forces are computed and used for the second update of the velocities. This requires the processor to know the positions of all atoms within the interaction cutoff, that have to be communicated from the processors assigned to the blocks that are at distance inferior or equal to the cutoff. We will call this step, which also involves local communications (but that may involve more distant processors than the previous one) “position comm” step. Once this is done, the algorithm loops back to the first step.
The communication volume involved in the position comm step can be reduced by taking into account the pairwise nature of the fundamental operations needed to compute the forces. Given a pair of atoms, in fact, one needs to choose which processor will perform the elementary force computation. This can be done on the basis of a geometrical argument. Among the various methods, that are also called neutral territory approaches,38 we choose the one presented by Shaw et al.,16 known as the midpoint method.38 This method picks out the processor that computes an interaction between two atoms as the one assigned to the subdomain where the center of the segment between the two atoms lies. As a consequence, each processor only needs to import information about atoms located at less than 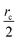 from its block: one can show that the communication volume is then, with d being the size of an edge of a subdomain,
from its block: one can show that the communication volume is then, with d being the size of an edge of a subdomain,  as represented schematically in Fig. 2. This is a significant reduction with respect to the naive method,38 especially at a high processors count. Note, however, that within this scheme, a processor might need to compute the elementary interaction between atoms that do not belong to its block.
as represented schematically in Fig. 2. This is a significant reduction with respect to the naive method,38 especially at a high processors count. Note, however, that within this scheme, a processor might need to compute the elementary interaction between atoms that do not belong to its block.
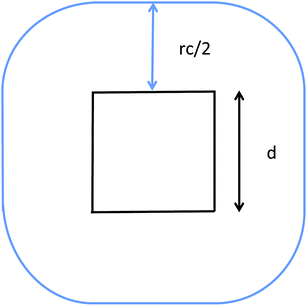 | ||
| Fig. 2 Illustration of the midpoint rule in 2D: the square of edge d represents a subdomain assigned to a process and the blue line delimits the area that has to be imported by the latter. | ||
Furthermore, once the elementary pairwise computation has been done, we can take advantage of Newton's third law and communicate the force back to both processors from which the positions originated (“force comm” step). This additional communication cost is in general negligible compared to the computational gain represented by the reduction of the computations of the forces by half.
Additionally, the midpoint approach is simple enough not to complicate too much the implementation, which is ideal for a platform like Tinker-HP, meant to be shared with a community of developers. Nevertheless, more elaborate techniques are interesting and have been shown to reduce asymptotically the amount of data that need to be communicated in the “position comm” step and in the “forces comm” step. We are currently studying these methods in the context of PFF to compare them to the present midpoint approach. Some of them should appear in future releases of our code.
The algorithmic structure of a parallel (short-range) MD step with spatial decomposition is shown in Fig. 3.
To address load balancing issues that may appear in non-homogeneous systems (when equally sized subdomains contain a very different number of atoms), a procedure in which the size of the subdomains is iteratively changed has been implemented.
2.2 Distributed memory for simulations using point dipole models
Distributed memory parallelism allows one to scatter the memory among the processors and thus to run simulations that would not be possible because of memory limitations. In Tinker-HP, almost all data are distributed, this being possible by reallocation of dynamically allocated arrays at regular intervals. For example, during the computation of the non-bonded forces at a O(N) computational cost using the linked-cell method,39 the neighbor lists used, that are the most memory-consuming data structures of the program, are reallocated at the same frequency as they are updated. This is an important aspect allowing Tinker-HP to remain efficient on small computer clusters and desktop stations as the list builder will adapt to the situation.Unfortunately, some data structures such as the arrays containing the global parameters are allocated once and for all and cannot be distributed. This is especially problematic for PFFs such as AMOEBA, that require more parameters than the classical ones: replicating these arrays for each processor would be prohibitive. This issue can be circumvented by using shared memory segments that can be managed with MPI (3.X) directives. This means that these data are allocated only once per node and are accessible by every processor within the node, reducing thus memory requirements by the number of processors of the node.
2.3 Adaptation of the 3D spatial decomposition to point dipole polarizable force fields
In this section, we will explain how the global concepts of 3D spatial decomposition can be adapted to the special case of the computation of the polarization energy and forces in PFFs. To our knowledge this is the first functional production implementation of such a technique in that context. Indeed, some of us proposed recently a 1D spatial decomposition40 implementation for AMOEBA. Here we propose a full extension to a 3D spatial decomposition to benefit from further performance enhancements. We will limit ourselves to the induced dipole model that is used in AMOEBA and that is the one implemented in Tinker-HP but the methodology is general and can be applied to various types of point dipole models.The computation of the polarization energy in PFFs using the induced dipole formulation consists of two steps. First, a set of 3N (N being the number of polarizable sites) induced dipoles has to be computed by minimizing the functional
| Tμ = E, | (1) |
The computation of the induced dipoles by iterative methods represents not only an important additional computational cost, but also an important communication cost, as at each iteration two of the three communication steps described in Section 2 are required.
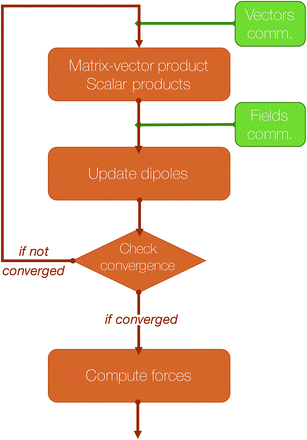
An essential part of our parallelization strategy is masking communication by computation in the parallel solvers whenever possible. This is achieved by using non-blocking MPI routines and by starting the receptions and the sendings of data as soon as possible, and, at the same time, verifying that the communications are finished as late as possible in the code, so that computations are being made between these two states. A schematic representation of a typical iteration of a polarization solver is shown in Fig. 4.
3 Parallel algorithm for point dipoles using smooth particle mesh Ewald
We present here new developments concerning the use of SPME (Smooth Particle Mesh Ewald) using distributed multipole electrostatics and polarizable point dipole models. Building on our previous work40 where we proposed a 1D decomposition of the distributed SPME grids, we now extend this formalism to the use of 2D pencil decomposition. Such an approach offers strongly improved performances especially when coupled to efficient iterative and non-iterative Krylov polarization solvers. In the previous section we focused the discussion on the parallelization strategy for short-range interactions. These include the bonded and van der Waals interactions, as well as the short range portion of the electrostatic and polarization interactions. The long-range part of such interactions needs to be handled separately, with a strategy that depends on the boundary conditions used for the simulation. Two main strategies exist in this regard: explicit solvent in periodic boundary conditions (PBC) and implicit solvation models. In this section, we focus on PBC. The additional possibility offered by Tinker-HP of treating the boundary with a polarizable continuum solvation model, namely, the Conductor-like Screening Model44–46 (COSMO), is presented in Section 6.As we stated before, the method that we adopt for PBC is the Smooth Particle-Mesh Ewald47 (SPME). It has become a standard algorithm in modern biomolecular simulations to compute electrostatic interactions in periodic boundary conditions, thanks to its advantageous 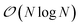 scaling. The method has been extended to PFFs48 as well as to multipolar interactions,49 possibly including penetration effects.50
scaling. The method has been extended to PFFs48 as well as to multipolar interactions,49 possibly including penetration effects.50
Let us explain the steps that are followed during a SPME computation for the electrostatic potential produced by distributed multipoles. The exact same considerations apply to the computation of the electrostatic and polarization forces and during a MVP computation during the iterative solution of the polarization equations. The electrostatic interactions are divided into two parts, one of which is short-range and is treated in the direct space, while the other is long-range and is treated in Fourier space. For the first, short-range part, the consideration made in Section 2 apply: we focus here on the reciprocal space computation. Such a computation requires the definition of a 3D grid and the use of Fast Fourier Transforms, which requires a significantly different parallelization strategy. The most standard one uses a 1D or 2D decomposition of the 3D grid and has been described elsewhere12,40 in detail. Let us summarize its main steps and analyze the parallelization strategy employed in Tinker-HP.
The SPME computation requires to distribute the multipoles on the grid using a B-spline interpolation and then to solve Poisson's equation in the reciprocal space. The distribution of the 3D grid is therefore what drives the parallelization strategy. In Tinker-HP, the grid is decomposed into 2D pencils, and each pencil is assigned to a processor. The first step of SPME consists into assigning charges or higher order multipoles to the gridpoints. As explained in our previous work,40 this operation requires local communications between processors assigned to neighboring portions of the grid.
The second step consist into switching to Fourier space by applying a forward FFT to the grid that has just been filled. In Tinker-HP, this is entirely handled by the 2DECOMP&FFT library.51,52
Then, the convolution with a pair potential47 is done in Fourier space, which is a simple multiplication that is naturally distributed among the processors without any necessary communication.
Finally, the result of this multiplication is transformed back to real space by applying a backward FFT, which is also taken care of by 2DECOMP&FFT in Tinker-HP.
A final local set of communications between processors responsible for neighboring portions of the grid is done, followed by local multiplication with B-splines. A schematic representation of these steps is shown in Fig. 5.
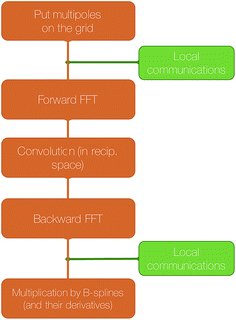 | ||
| Fig. 5 Schematic representation of the computation of the reciprocal part of the electrostatic energy and forces with SPME. | ||
Naturally, because the Fourier space decomposition of the grid may not fit exactly the 3D spatial decomposition, additional communications of positions are required before starting the reciprocal part of a SPME computation. Furthermore, when electrostatic or polarization forces are computed in this way, or after a matrix-vector multiplication in an iteration of a polarization solver, communication of some of these forces or dipoles are required.
Lagardère et al. showed40 that the reciprocal part of SPME presented just above does not scale as well as the direct part with the number of processors, because of the relatively poor parallel scaling of the FFTs. Furthermore, because reciprocal space and direct space computations are independent and because reciprocal space is usually computationally cheaper, a usual strategy is to assign a smaller group of processors to reciprocal space and the rest to the direct space. This strategy can be used in Tinker-HP for both permanent electrostatics and polarization.
In that case, a difficulty arises in PFF computations. The load balancing between direct and reciprocal space computations is in fact essential to achieve a good scalability. However, the relative cost of direct and reciprocal computations is different for permanent electrostatics and MVP required for the computation of the induced dipoles. At this moment, only heuristic strategies have been implemented in Tinker-HP to handle this problem.
4 Software possibilities
Tinker-HP is part of the Tinker 8 package and consequently it is fully compatible with the canonical Tinker and the Tinker-OpenMM (GPU) codes. Therefore, all Tinker's analysis and visualization tools are available with Tinker-HP. Details about these possibilities are not described here and can be accessed on the Tinker community website (http://tinkertools.org). The Tinker-HP source code is freely available to the academic community: details and downloading informations can be found on the Tinker-HP website (http://www.ip2ct.upmc.fr/tinkerHP). In the following section, we detail the possibilities of the code that will be contained in the incoming public releases.4.1 Polarizable molecular dynamics engine features
It is important to point out that an important choice in the Tinker-HP strategy is to keep accuracy to the maximum by retaining a double-precision approach. By definition, GPUs have the strong advantage of using mixed precision which has been shown to produce more stability than simple precision computations. The strategy here is to build on the availability of the double precision to use algorithms that should/could not be used in mixed precision but are expected to be fully operational and faster in our case. For example, any CG methods are sensitive to precision (the symmetry of matrices being lost) as is the case for predictor-correctors such as the ASPC. Tinker-HP offers a full use of these strategies and compensates for the extra computational cost of double precision by more dependable algorithms.
4.2 Available force fields
5 Benchmarks and applications using the AMOEBA polarizable force field
The present implementation has been extensively tested and reaches exactly the same accuracy as the canonical Tinker for polarizable force field when considering analogous algorithms, allowing Tinker-HP to produce reference computations. All the proposed benchmarks use the AMOEBA force field. We tested the performances of Tinker-HP on various systems. We studied the scalability of the code dealing with homogeneous systems such as bulk water, and inhomogeneous systems ranging from ionic liquids to proteins. Finally we tested our approach on very large biosystems.5.1 Computer platforms
All tests have been performed on the Occigen machine at GENCI (CINES, Montpellier, France) and at CYFRONET (Krakow, Poland) on the Prometheus machine. Occigen is a Bullx DLC with Intel Xeon E5-2690 v3 (24 Haswell cores at 2.6 GHz per node) and Intel Xeon E5-2690 v4 (28 Broadwell cores at 2.6 GHz per node), Infiniband FDR and 128 Go of memory per node. Prometheus is a HP Apollo 8000 with Intel Xeon E5-2680 v3 (24 Haswell cores at 2.5 GHz per node), Infiniband and 128 Gb of memory per node. For consistency, all results are given for Haswell processors. We observed an average four per cent gain in speed on the Broadwell configuration, especially for a suboptimal number of cores, i.e. before the scaling limit. Some timings have been obtained using Tinker-OpenMM on GPU cards (NVIDIA GTX 970 and GTX 1080), the best GPU results (GTX 1080) can be found in Table 3 below, the GTX 970 productions being roughly half of the GTX 1080 ones.5.2 Simulations setup
Benchmark simulations (except free energies) were made in the NVT ensemble with a Verlet/RESPA multi-time step integrator with either a 2 fs or a 3 fs time-step (using hydrogen mass re-partitioning in the latter case) for the non-bonded forces and half of this value for the bonded forces. Two Krylov solvers were considered here: iterative PCG and non-iterative TPCG, both using a diagonal preconditioner.41,42 Note that we report here the first results ever using TCG coupled to SPME. The convergence criterion for the PCG iterative solver was set to 10−5 D. Electrostatics and polarization interactions were treated using the PME algorithm with a real space Ewald cutoff of 7.0 Å. The van der Waals cutoff was set 9.0 Å without any long-range correction.5.3 Homogeneous systems: water boxes and ionic liquids
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms up to 23.3 millions atoms. Table 1 summarizes the characteristics of these boxes: their size in Angstroms, the number of atoms they contain, the size of the associated PME grid and the name with which they will be referenced in the rest of the paper.
000 atoms up to 23.3 millions atoms. Table 1 summarizes the characteristics of these boxes: their size in Angstroms, the number of atoms they contain, the size of the associated PME grid and the name with which they will be referenced in the rest of the paper.
| System | Puddle | Pond | Lake | Sea | Ocean |
|---|---|---|---|---|---|
| Number of atoms | 96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
288![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 640 640![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 776 776![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 328 328![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| Size (of an edge) in Angstroms | 98.5 | 145 | 205.19 | 426.82 | 615.57 |
| Size (of an edge) of the PME grid | 120 | 144 | 250 | 432 | 648 |
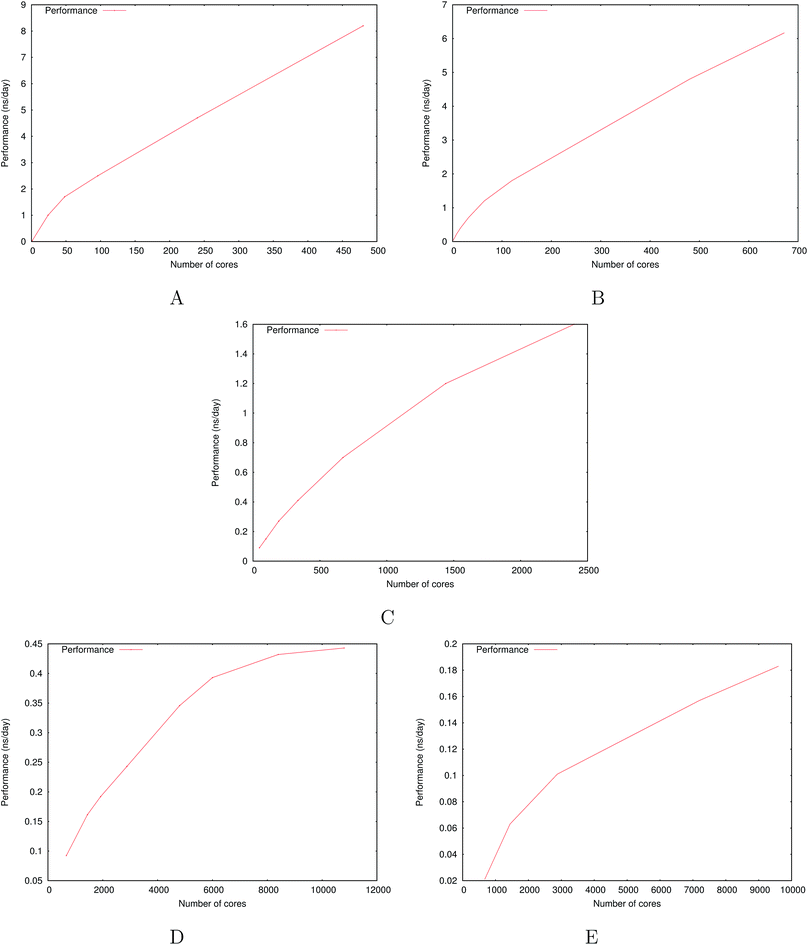
Fig. 6 show the detailed scalability up to almost 1 million atoms.
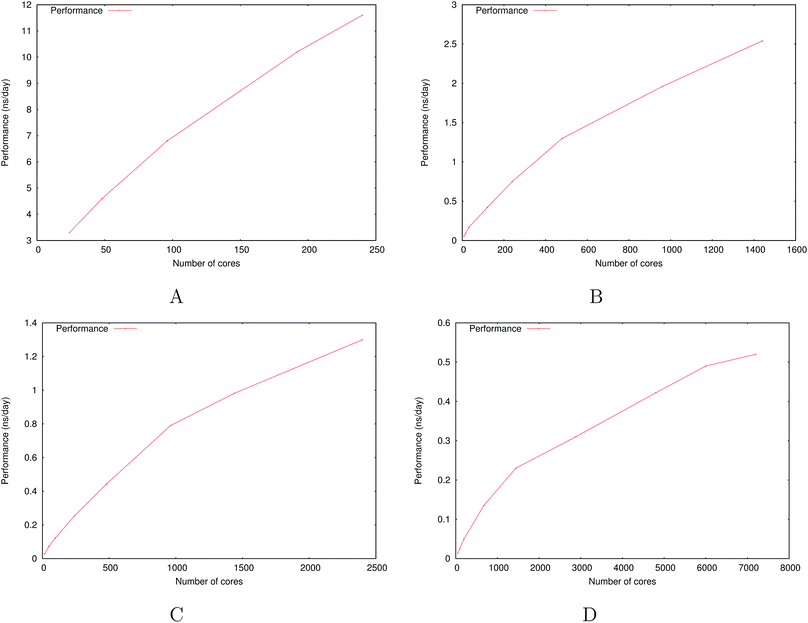 | ||
| Fig. 6 Performance gain for the [dmim+][cl−] ionic liquid system (A) and the Puddle (B), Pond (C) and Lake (D) water boxes. | ||
A very good scalability is observed in the three cases. Table 3 displays the best production timings in ns per day. The code appears to be competitive with the GPU numbers extracted from Tinker-OpenMM even for a system such as the smallest waterbox test (Puddle, 96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms). In this case, Tinker-HP is already 1.5 faster than a GTX 1080 card (3 times for a GTX 970) but with double precision compared to mixed precision arithmetics used by GPUS. As we will discuss later in the case of proteins, the newly introduced 3D domain decomposition algorithmic for polarizable FF becomes more beneficial when the size of the system grows and a first advantage of Tinker-HP is to be able to use the distributed memory system of the CPU platform. Also for such large systems numerical instabilities of the polarization solvers that result in energy drifts40–43 are a key error that must be contained. Double precision is highly preferable when one wants to use advanced conjugate gradient solvers (and Krylov approaches in general). Tinker-HP has an advantage as it affords mathematically robust solutions for “drift-free” polarization solvers (Truncated Conjugate Gradient, TCG42,43) with analytic forces. Such techniques allow for (very) long simulations. A stable adaptation of these methods to mixed precision hardware (i.e. GPUs) is underway but is mathematically non-trivial. Note that for short to medium simulations of a few dozen ns, the discussion is without object as the drifting issue will remain negligeable offering a full applicability of GPUs acceleration. However, towards and beyond the microsecond, the analytical forces polarization solvers will be key for stable polarizable simulations. For the other benchmark cases, the speedup increases to a 5 and 6-fold over a GTX970 (2 and 3-fold over a GTX1080) for 288
000 atoms). In this case, Tinker-HP is already 1.5 faster than a GTX 1080 card (3 times for a GTX 970) but with double precision compared to mixed precision arithmetics used by GPUS. As we will discuss later in the case of proteins, the newly introduced 3D domain decomposition algorithmic for polarizable FF becomes more beneficial when the size of the system grows and a first advantage of Tinker-HP is to be able to use the distributed memory system of the CPU platform. Also for such large systems numerical instabilities of the polarization solvers that result in energy drifts40–43 are a key error that must be contained. Double precision is highly preferable when one wants to use advanced conjugate gradient solvers (and Krylov approaches in general). Tinker-HP has an advantage as it affords mathematically robust solutions for “drift-free” polarization solvers (Truncated Conjugate Gradient, TCG42,43) with analytic forces. Such techniques allow for (very) long simulations. A stable adaptation of these methods to mixed precision hardware (i.e. GPUs) is underway but is mathematically non-trivial. Note that for short to medium simulations of a few dozen ns, the discussion is without object as the drifting issue will remain negligeable offering a full applicability of GPUs acceleration. However, towards and beyond the microsecond, the analytical forces polarization solvers will be key for stable polarizable simulations. For the other benchmark cases, the speedup increases to a 5 and 6-fold over a GTX970 (2 and 3-fold over a GTX1080) for 288![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms (Pond) and 864
000 atoms (Pond) and 864![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms (Lake) water boxes respectively. For the Lake box, a detailed analysis of the scaling against ideal scaling is provided in ESI S2.† We then pushed the code towards its limits by testing very large systems including 7
000 atoms (Lake) water boxes respectively. For the Lake box, a detailed analysis of the scaling against ideal scaling is provided in ESI S2.† We then pushed the code towards its limits by testing very large systems including 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 776
776![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 23
000 and 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300
300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms respectively. At these levels, GPUs have memory limitations that makes such simulations impossible, which is not the case with supercomputers relying on distributed memory. These “computational experiments” took place on the Prometheus supercomputer (CYFRONET, Krakow, Poland) and enabled us to test for the validity of the code on a very large scale. Results show that Tinker-HP is still operational beyond 20 million atoms. Of course, the production really slows down to a few dozen ps per day but the performance is noticeable as it would be quite enough to compute properties such as electrostatic potentials or even a short ns-scale molecular dynamics. Thus, one can expect, depending on the machine used, to produce a ns in a few weeks on the largest Ocean water box using TCG2/RESPA (3 fs). It is worth noticing that the largest computation was limited only by the computer system availability and that presently larger systems are potentially accessible with more computational resources. However, such very large computations require a different setup than the others due to memory limitations and communication issues. Indeed, for such a large number of atoms, FFTs really become severely time limiting and intra-node communications strongly affect performances. One solution that was used for Ocean was to only use a fraction of the cores of a node to take advantage of the node memory without suffering from excessive communications. That way, if the Ocean test ran on 12
000 atoms respectively. At these levels, GPUs have memory limitations that makes such simulations impossible, which is not the case with supercomputers relying on distributed memory. These “computational experiments” took place on the Prometheus supercomputer (CYFRONET, Krakow, Poland) and enabled us to test for the validity of the code on a very large scale. Results show that Tinker-HP is still operational beyond 20 million atoms. Of course, the production really slows down to a few dozen ps per day but the performance is noticeable as it would be quite enough to compute properties such as electrostatic potentials or even a short ns-scale molecular dynamics. Thus, one can expect, depending on the machine used, to produce a ns in a few weeks on the largest Ocean water box using TCG2/RESPA (3 fs). It is worth noticing that the largest computation was limited only by the computer system availability and that presently larger systems are potentially accessible with more computational resources. However, such very large computations require a different setup than the others due to memory limitations and communication issues. Indeed, for such a large number of atoms, FFTs really become severely time limiting and intra-node communications strongly affect performances. One solution that was used for Ocean was to only use a fraction of the cores of a node to take advantage of the node memory without suffering from excessive communications. That way, if the Ocean test ran on 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 288 cores on 512 nodes, we used only 6 cores/node (on 24) to actually perform the computation. This gave us the possibility to better use the bandwidth of the interconnect cards (by reducing contention in MPI transfers between cores and cards), a strategy that compensates for the lack of active cores and that can be used for any system size. We used the same strategy to a lower extent for Sea as 17 cores out of 24 were active. Overall, a rough estimate for the fastest Broadwell CPU configuration (Occigen) is that using a RESPA (3 fs)/TCG2 setup, a routine production of 1 ns per day is reachable for a million atoms. Such a value is a combination of various hardware setups that are not only dependent on the CPU speed (and numbers), as the interconnection cards have a strong influence on the final results (Fig. 7).
288 cores on 512 nodes, we used only 6 cores/node (on 24) to actually perform the computation. This gave us the possibility to better use the bandwidth of the interconnect cards (by reducing contention in MPI transfers between cores and cards), a strategy that compensates for the lack of active cores and that can be used for any system size. We used the same strategy to a lower extent for Sea as 17 cores out of 24 were active. Overall, a rough estimate for the fastest Broadwell CPU configuration (Occigen) is that using a RESPA (3 fs)/TCG2 setup, a routine production of 1 ns per day is reachable for a million atoms. Such a value is a combination of various hardware setups that are not only dependent on the CPU speed (and numbers), as the interconnection cards have a strong influence on the final results (Fig. 7).
5.4 Speeding up free-energy computations: assessing large water box hydration free energies computations
The observed speed-up on water boxes led us to test the performance AND the accuracy of free energy computations using large water boxes to compare them to initial works using AMOEBA and the canonical Tinker software. The hydration free energies for water, benzene, K+ and Na+ were calculated by summing up the free energies of three thermodynamic steps, solute discharging in a vacuum, solute van der Waals coupling with solvent, and solute recharging in solvent. For K+ and Na+, since the standard state in simulation was 1 mol L−1 and the standard state in experiment was 1 atom, the free energy difference between the two states of 1.87 kcal mol−1 was added to the final results. The softcore van der Waals potential was used as in our latest work with Tinker. A total of 21 alchemical states were considered, and a 2 ns NVT simulation was performed at each state. The RESPA (2 fs) integrator was employed as the temperature was maintained at 298 K by the Bussi thermostat. The vdW interaction was truncated at 12.0 Å as SPME used a real-space cutoff of 8.0 Å and a 72 × 72 × 72 grid. The Bennet Acceptance Ratio (BAR)73 method was used to extract the free energies between states. In order to test the computation efficiency, the solute molecule was immersed in a large cubic simulation box of 6000 water molecules. The length of the box was 56 Å and 192 cores were used for each simulation with 48 dedicated cores for PME. This number of core is suboptimal but already provides a very good speedup as all windows were launched simultaneously on a total of 4032 cores, a computer resource that is commonly accessible in modern computer centers. Each total free energy evaluation took 18 hours to complete using a PCG coupled to Kolafa's predictor-corrector (ASPC) algorithm with a 10−5 convergence threshold. The hydration free energies for water, benzene, sodium and potassium are listed in the table of the ESI S1,† together with results from previous work. For all four solute molecules, there is excellent agreement between Tinker-HP and previous simulations using either BAR or OSRW (Orthogonal Space Random Walk) method.74 The values converge at 2 ns with a statistical error of around 0.1 kcal mol−1. The hydration free energies for potassium obtained from Tinker-HP and the Tinker published results are slightly different because the Tinker historical work did not use the softcore van der Waals potential at that time, but appears fully consistent with the present canonical Tinker result. Overall, Tinker-HP appears reliable and very efficient for the calculation of solvation free energies with huge gain in terms of computation time. Of course, further tests on more complex free energy computations are required to test all the possible combinations of TCG and RESPA algorithms. If TCG2 is really accurate and fast, TCG1 is significantly faster but these procedures have not been extensively tested yet and their evaluation concerning their applicability to free energy computations will be the subject of a larger study. In any case, TCG2 would lead to a computing time reduction of the same computations to roughly 14.5 hours and TCG1 to 12.5 hours. Such studies will benefit from the computational platform introduced in Tinker-OpenMM that allows computing absolute binding and relative alchemical approach as well as relative binding affinities of ligands to the same host. As an immediate other perspective, the OSRW results extracted from the canonical Tinker are presented in the table. This approach leads to very similar results to the BAR approach but requires up to 5 times less computer time. OSRW is currently under implementation in Tinker-HP. These results give an idea about the new possibilities offered by massive parallelism for free energies evaluations: the discussed simulations that initially took months are now possible within half a day and soon in a couple of hours with OSRW within Tinker-HP.5.5 From proteins to realistic biosystems
To study the scalability and applicability of the Tinker-HP platform to complex non homogeneous systems, we tested various systems starting from the “small” ubiquitin protein (9737 atoms), and prototypic dihydrofolate reductase (dhfr, 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 558 atoms) which is the reference protein test case extracted from the joint AMBER/CHARMM benchmark (http://ambermd.org/amber10.bench1.html). We push the code towards the simulation of very large biosystems tackling the COX-2 dimer, the Satellite Tobacco Mosaic Virus (STMV) and the ribosome full structures in polarizable water. All timings are obtained for equilibrated systems.
558 atoms) which is the reference protein test case extracted from the joint AMBER/CHARMM benchmark (http://ambermd.org/amber10.bench1.html). We push the code towards the simulation of very large biosystems tackling the COX-2 dimer, the Satellite Tobacco Mosaic Virus (STMV) and the ribosome full structures in polarizable water. All timings are obtained for equilibrated systems.
The characteristics of the inhomogeneous systems simulations boxes used for benchmark are summed up in Table 2.
| Systems | Ubiquitin | Dhfr | COX-2 | STMV | Ribosome |
|---|---|---|---|---|---|
| Number of atoms | 9732 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 558 558 |
174![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 219 219 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 066 066![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 228 228 |
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 484 484![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 755 755 |
| Size (of an edge) in Angstroms | 54.99 × 41.91 × 41.91 | 62.23 | 120 | 223 | 327.1 |
| Size (of an edge) of the PME grid | 72 × 54 × 54 | 64 | 128 | 270 | 360 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms, which is 4 times the size of DHFR and 10 times that of Ubiquitin). Surprisingly, results remain competitive with GPUs which are fully taking advantage of their computing power for such a range of systems with low memory requirements. DHFR allows to study in depth the code behavior in that system size range. Indeed, the best production time for a use of all cores of a node brings us to a 7.69 ns per day using TCG2. This production time is really close to the 8.29 ns per day exhibited by Tinker-OpenMM on a GTX1080 (see Table 3). If we used the same number of cores distributed on more nodes, to use the same technique we used on the large ocean and sea water boxes, the performance extends to 8.79 ns per day. These numbers make Tinker-HP very competitive for these small systems on a reasonable number of cores that is easily accessible on modern supercomputers. In addition, one can note that most of the recent machines use Broadwell Xeon that gives slightly better performances by a few percents. In other words, Tinker-HP is able to compensate for the computational burden of the use of double precision thanks to its new algorithmics compared to the accelerated mixed precision GPUs thus reaching both speed and accuracy. A detailed analysis of the DHFR scaling against ideal scaling is provided in ESI S2.† As one could expect, the deviation to the ideal scaling is higher than in the case of the previously larger Lake water box: larger the system is, closer to the ideal scaling we get.
000 atoms, which is 4 times the size of DHFR and 10 times that of Ubiquitin). Surprisingly, results remain competitive with GPUs which are fully taking advantage of their computing power for such a range of systems with low memory requirements. DHFR allows to study in depth the code behavior in that system size range. Indeed, the best production time for a use of all cores of a node brings us to a 7.69 ns per day using TCG2. This production time is really close to the 8.29 ns per day exhibited by Tinker-OpenMM on a GTX1080 (see Table 3). If we used the same number of cores distributed on more nodes, to use the same technique we used on the large ocean and sea water boxes, the performance extends to 8.79 ns per day. These numbers make Tinker-HP very competitive for these small systems on a reasonable number of cores that is easily accessible on modern supercomputers. In addition, one can note that most of the recent machines use Broadwell Xeon that gives slightly better performances by a few percents. In other words, Tinker-HP is able to compensate for the computational burden of the use of double precision thanks to its new algorithmics compared to the accelerated mixed precision GPUs thus reaching both speed and accuracy. A detailed analysis of the DHFR scaling against ideal scaling is provided in ESI S2.† As one could expect, the deviation to the ideal scaling is higher than in the case of the previously larger Lake water box: larger the system is, closer to the ideal scaling we get.
| Systems | Ubiquitin | DHFR | COX-2 | STMV | Ribosome |
|---|---|---|---|---|---|
| Number of atoms | 9737 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 558 558 |
174![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 219 219 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 066 066![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 628 628 |
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 484 484![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 755 755 |
| Tinker-HP number of CPU cores | 480 | 680(960) | 2400 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
| PCG (10−5 D, ASPC) | 8.4 | 6.3(7.2) | 1.6 | 0.45 | 0.18 |
| TPCG2 | 10.42 | 7.81(8.93) | 1.98 | 0.56 | 0.22 |
| TPCG2/RESPA (3 fs) | 15.62 | 11.71(13.39) | 2.98 | 0.84 | 0.34 |
| CPU OPEN-MP | 0.43 | 0.21 | 0.024 | 0.0007 | N.A. |
| GPU (GTX 1080) | 10.97 | 7.85 | 1.15 | N.A. | N.A. |
| Systems (water boxes) | Puddle | Pond | Lake | Sea | Ocean |
|---|---|---|---|---|---|
| Number of atoms | 96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
288![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
864![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 776 776![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
23.3 × 106 |
| Tinker-HP number of CPU cores | 1440 | 2400 | 7200 | 7104 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 288 288 |
| PCG (10−5 D, ASPC) | 2.54 | 1.3 | 0.52 | 0.062 | 0.0077 |
| TPCG2 | 3.10 | 1.59 | 0.63 | 0.076 | 0.01 |
| TPCG2/RESPA (3 fs) | 4.65 | 2.38 | 0.95 | 0.11 | 0.014 |
| CPU OPEN-MP | 0.050 | 0.014 | 0.003 | N.A. | N.A. |
| GPU (GTX 1080) | 2.06 | 0.80 | 0.21 | N.A. | N.A. |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 484
484![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 755 atoms. Presently, three days are necessary to produce a ns allowing for a very detailed study of such an important structure. We expect even free energy studies to be feasible. Various incoming studies will analyze more in-depth the use of PFFs to such mostly important biosystems.
755 atoms. Presently, three days are necessary to produce a ns allowing for a very detailed study of such an important structure. We expect even free energy studies to be feasible. Various incoming studies will analyze more in-depth the use of PFFs to such mostly important biosystems.
6 Beyond classical MD simulations in periodic boundary conditions
So far, we have presented the capabilities of Tinker HP in the context of PBC classical molecular dynamics simulations. We have discussed the parallelization strategy and showed benchmark results that demonstrate the scalability and performances of the code. While Tinker-HP is mainly a molecular dynamics code, it is not limited to PBC classical simulations and can be used for different applications. In particular, Tinker-HP offers the possibility of performing non-periodic MD simulation with a polarizable force field such as AMOEBA using a polarizable continuum solvation model as a boundary. This possibility is not our main choice for MD simulation and, as a consequence, has not been as thoroughly optimized as the PBC code. Furthermore, it involves a few computational steps that scale quadratically with respect to the size of the system, making it not suitable for the very large systems presented in Section 5. However, the possibility of computing the energy and forces with non-periodic boundary conditions and with a continuum boundary opens the way for using Tinker-HP as a module to handle the classical part in a polarizable QM/MM(/continuum) calculations,77–81 including the computation of molecular properties and ab initio multiscale QM/MM MD simulations. These calculations are usually dominated in computational cost by the QM part, making the quadratic scaling of the classical part a minor issue. Nevertheless, the scalability of Tinker-HP paves the way to large-scale polarizable multiscale simulations.In this section, we will describe the non-periodic code in Tinker-HP, based on the recently proposed ddCOSMO,45,46,82,83 a domain decomposition (dd) discretization of the conductor-like screening model.44 We will then discuss two complementary QM/MM strategies that can be used to couple Tinker-HP to a quantum-mechanical code.
6.1 Implicit solvent: ddCOSMO
Continuum solvation models84,85 (CSM) are a well-established technology in both quantum chemistry and MD. The CSM developed for MD are usually based on the Generalized Born (GB) Ansatz, or its multipolar generalization, which approximate the solution to the electrostatics equations in the presence of a continuum with an additive energy term. Methods developed in quantum chemistry rely, on the other hand, on a rigorous numerical solution of Poisson's equation. Such models are much more expensive than the GB counterpart; however, since these models have been developed for quantum mechanical calculations, and therefore for up to medium-sized systems, their computational cost is not a real limitation in QM calculations. Nevertheless, it has always prevented their application to MD simulations. The use of a polarizable CSM is of particular interest when a PFF is used due to the natural consistency between the two approaches. Recently, a new discretization to COSMO has been proposed. Such a new discretization, named ddCOSMO, has been developed when the molecular cavity is made of interlocking spheres (i.e., van der Waals cavity) and has been extensively described elsewhere.46 The dd approach offers huge advantages since the matrix to be inverted to solve the model at each time step is highly sparse: as a consequence, the model scales naturally linearly with the size of the system and the iterative solution to the ddCOSMO equations is perfectly suited for a parallel implementation in which the spheres that constitute the cavity are distributed among cores.The parallelization strategy adopted for the ddCOSMO implementation follows the spatial decomposition logic discussed in Section 2. Again, we divide the space occupied by the system into blocks and assign a block to each CPU. The CPU is then responsible for updating the positions, speeds and accelerations of the atoms belonging to it block. However, there are two important differences compared to the spatial decomposition discussed for short-range interactions. First, the space occupied by the solute is not a cube or a regular geometrical configuration but rather a cavity whose shape depends on the configuration of the solute. Second, the cavity is not fixed during the simulation as it evolves with the solute.
To address the first issue, we define the blocks by enclosing the solute in the smallest parallelepiped containing it and we divide this parallelepiped into smaller ones. This strategy presents the advantage of allowing us to reuse the whole machinery that has been described in Section 2. However, such a strategy can imply potential load balancing issues that require to be addressed, especially when a high number of processors is used. Again, an iterative procedure has been implemented to determine the optimal sizes of the sub-domains.
To solve the second issue, one should in principle recompute the enclosing parallelepiped at each time step. To avoid the cost of performing such an operation, we build a slightly larger parallelepiped and recompute its geometry only once every few MD steps (n = 20 for example).
In Tinker-HP, the solution to the ddCOSMO linear equations is computed by using the JI/DIIS iterative solver also used for the polarization eqn (1). The iterative procedure requires to compute MVP with the sparse ddCOSMO matrix, which can be done both very efficiently and involving only local communications. However, the right-hand side of the ddCOSMO equations depends on the electrostatic potential created by the solute's permanent and induced multipoles. In the current implementation, the potential is computed via a double loop, which implies a 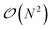 computational cost. Furthermore, an “all to all” communication of the positions of the system is required prior to this computation.
computational cost. Furthermore, an “all to all” communication of the positions of the system is required prior to this computation.
Thus, the computational bottleneck in terms of both computational complexity and parallel efficiency lies in the computation of the right-hand side. If AMOEBA/ddCOSMO MD simulations have been shown to be possible,46 this kind of boundary is not competitive with SPME in term of pure polarizable MD production. However, as we stated at the beginning of this section, the advantage of the ddCOSMO implementation is to provide a boundary condition for multiscale simulations. In particular, having non-periodic boundary conditions is ideal when working with localized basis functions in QM computations.
Detailed benchmark results of the current parallel implementation are presented in ESI S3.†
6.2 Multiscale modeling and polarizable QM/MM
The PFF/ddCOSMO framework described in this section is a starting point for multiscale, polarizable QM/MM simulations. This is a fundamental direction for Tinker-HP as PFFs such as AMOEBA provide a high-quality embedding strategy for QM systems with various potential applications. For instance, in a recent publication, some of us showed how a DFT-based QM/AMOEBA description is able to model electronic excitations in aqueous solution80 for systems that interact in a specific and structured way with the environment. An ab initio QM/MM MD strategy has also been recently proposed.81The present QM/MM possibilities of Tinker-HP follow two complementary strategies. Tinker-HP can be used as an external embedding tool, or can be directly coupled to a QM code in order to obtain a fully self-consistent polarizable QM/MM implementation.
The first strategy is the one followed in LICHEM77 (Layered Interacting CHEmical Model), that provides a QM/MM interface with unmodified quantum chemistry software suites such as Gaussian,86 PSI4,87 and NWChem88 to perform QM/MM calculations using the AMOEBA force field. This is done by approximating AMOEBA's multipolar distribution, with a set of point charges,89 which can then be read by the QM code. This choice is motivated by the idea of developing an interface with existing QM codes with non-native multipolar QM/MM capabilities. LICHEM extracts forces and energies from unmodified QM packages to perform a variety of calculations for non-bonded and bonded QM/MM systems, the latter by using the pseudobond formalism explicitly extended for QM/MM with PFFs.77,90,91 The calculations available in LICHEM include geometry and reaction path optimizations, single-point energy calculations, Monte Carlo, PIMD, etc.
Currently, the polarization component for the QM/MM interaction term in LICHEM is not fully self-consistent due to the use of unmodified QM codes. This is because only the field from the permanent multipoles from the MM subsystem is included in the effective Hamiltonian for the polarization component of the QM/MM interaction. However, as has been shown previously, this approximation, coupled with the fact that the QM and MM subsystem polarization is fully considered results into the recovery of over 80% of the total QM/MM self-consistent polarization.77,92
For the computation of electronic properties and full hybrid MD simulations, a second QM/MM approach can be pursued. This approach proposes a fully self-consistent treatment of the electronic density and the MM polarization and requires a modification of the QM self-consistent field routines. A QM/AMOEBA implementation that couples Tinker-HP to a locally modified version of the Gaussian suite of programs86 has been recently introduced.80,81 Such a strategy enables to use a DFT/AMOEBA based polarizable QM/MM strategy to compute the energy and response properties of an embedded system, as well as to perform Born–Oppenheimer (BO) hybrid QM/MM MD. The latter is accelerated through the use of an extended BO Lagrangian approach (XL-BO),93 which provides enhanced guess for the electronic density at every time step and allows for a stable hybrid MD with enhanced energy conservation.
In short, Tinker-HP offers additional advanced QM/MM functionalities with polarizable force fields. The continuous investigation efforts in our groups have the objective to bring sampling capabilities in a multiscale polarizable environment dedicated to electronic structure as sampling has been shown to be a key issue for predictive studies.80
7 Conclusion and perspectives
Our results demonstrate that molecular dynamics simulations with advanced point dipole polarizable force fields using distributed multipoles should no longer be qualified as slow anymore. The Tinker-HP software offers an efficient environment that enables one to perform large scale relatively long MD simulations on various complex systems encompassing several million atoms thanks to the new extension of 3D spatial decomposition to polarizable models coupled to advanced Krylov polarization solvers. It is able to ensure accuracy and speed as it exploits double precision, thanks to its new algorithmics able to circumvent the computational burden providing both additional speedups and mathematical robustness. For small systems, Tinker-HP is competitive with the present GPU implementation of Tinker (Tinker-OpenMM) whereas strong gains are observed for medium systems offering several thousand-fold acceleration compared to single core computations. For large systems, Tinker-HP remains the only operational Tinker code as it is able to efficiently distribute memory among nodes. We believe that this new tool will be of interest for the community of modelers, who will be able to perform meaningful simulations to test the applicability and discuss advantages of polarizable potentials. Of course, such developments will first find an echo in the field of chemistry where extreme accuracy matters, for example using embeddings of QM methods by PFFS that are beneficial to compute properties and where double precision is mandatory. For biophysics, where extreme sampling is required, the full application of PFFs remains a daunting task as present AMOEBA simulations, despite the discussed acceleration on large systems, still require weeks of computation. However, a few microseconds simulations are now technically possible and some applications such as free energy computations are completely accessible. In some way, PFFs are now able to produce simulations that classical force fields were able to generate a few years ago on similar platforms. The one-order of magnitude difference in speed of PFFs compared to classical FFs (when one considers the same computational platform, i.e. CPU or GPU), will remain due to the lower functional form complexity of the latter. However, the acceleration gains observed in optimal timings for codes like AMBER, NAMD, GROMACS or equivalent, are all obtained using GPU accelerators and through many years of optimization. Still, an important point to evaluate the future of PFF simulations is the fact that we have been really conservative in our present discussed benchmarks and optimization is only starting. Issues of precision, cutoffs, convergence criteria and vectorization will be addressed and will generate strongly improved performances. Note that the Tinker-HP methodology is not limited to CPUs. Indeed, the Tinker-HP FORTRAN legacy code will benefit from GPU acceleration as FORTRAN portability strategies exist and are under investigation (Hybrid-Fortran94 and OpenACC95). For CPUs, we also expect strong performance gains on new generation “big core” Xeon (Skylake and successors) and “small core” Xeon-Phi (Knight Landings) processors thanks to vectorization efforts exploiting AVX512 instructions without sacrificing double precision. Finally, Tinker-HP will be synchronized with Tinker-OpenMM34 opening our developments to the OpenMM community. Various method developments, already present in the Tinker community, will be integrated in the next version of the code, keeping in mind the mandatory philosophy to include only well-understood and scalable techniques. The high-performance implementation of additional multipolar polarizable force fields will be performed including the SIBFA26 (in progress), MPID96 (multipole and induced dipoles, the mapping of the CHARMM Drude polarizable force field on induced dipoles) and AMOEBA 2 models. Efforts will also be devoted to the porting of the third generation GEM (Gaussian Electrostatic Model) polarizable force field that relies on frozen distributed densities.30,97,98 The present technology will be complemented by massively parallel Monte-Carlo approaches, Langevin, constant-pH and various types of accelerated molecular dynamics. Advanced sampling techniques such as OSRW74 and replica exchange will be added. Concerning multiscale QM/MM simulations, studies towards coupling with linear scaling QM approaches will be pursued to continue to speed up hybrid MD simulations.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was made possible thanks to the French state funds managed by the CalSimLab LABEX and the ANR within the Investissements d’Avenir program (reference ANR-11-IDEX-0004-02) and through support of the Direction Générale de l’Armement (DGA) Maîtrise NRBC of the French Ministry of Defense. Funding from French Centre National de la Recherche (CNRS) is also acknowledged (PICS international collaboration grant (Sorbonne U.-UT AUstin) and Infiniti fund), as well as support by the National Institutes of Health (R01GM106137, R01GM114237 and R01GM108583), CPRIT (RP160657) and the Robert A. Welch Foundation (F-1691). This material is based upon work supported by the National Science Foundation Graduate Research Fellowship under Grant No. DGE-1610403. The authors are also indebted to the Texas Advanced Center (TACC, Austin, USA) and to the ISCD (Institut des Sciences du Calcul et des Données, Sorbonne U., France) for providing a development access for the initial design of this code. Production computations have been performed at GENCI (grant no. A0010707671) on the Occigen supercomputer (CINES, Montpellier, France). The authors are grateful to the CYFRONET computer center in Krakow (Poland) which provided help and resources to perform some of the large scale simulations of the paper on the Prometheus machine. LL, LHJ and JPP thank Cédric Bourasset and David Guibert (Centre for Excellence in Parallel Programming, ATOS-Bull) for fruitful discussions.References
- J. Huang, S. Rauscher, G. Nawrocki, T. Ran, M. Feig, B. L. de Groot, H. Grubmueller and A. D. MacKerell Jr, Nat. Methods, 2017, 14, 71–73 CrossRef CAS PubMed.
- J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, J. Chem. Theory Comput., 2015, 11, 3696–3713 CrossRef CAS PubMed.
- M. J. Robertson, J. Tirado-Rives and W. L. Jorgensen, J. Chem. Theory Comput., 2015, 11, 3499–3509 CrossRef CAS PubMed.
- M. M. Reif, P. H. Honenberger and C. Oostenbrink, J. Chem. Theory Comput., 2012, 8, 3705–3723 CrossRef CAS PubMed.
- J. W. Ponder and D. A. Case, Adv. Protein Chem., 2003, 66, 27–85 CrossRef CAS PubMed , Protein Simulations.
- B. R. Brooks, C. L. Brooks, A. D. Mackerell, L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels, S. Boresch, A. Caflisch, L. Caves, Q. Cui, A. R. Dinner, M. Feig, S. Fischer, J. Gao, M. Hodoscek, W. Im, K. Kuczera, T. Lazaridis, J. Ma, V. Ovchinnikov, E. Paci, R. W. Pastor, C. B. Post, J. Z. Pu, M. Schaefer, B. Tidor, R. M. Venable, H. L. Woodcock, X. Wu, W. Yang, D. M. York and M. Karplus, J. Comput. Chem., 2009, 30, 1545–1614 CrossRef CAS PubMed.
- A.-P. E. Kunz, J. R. Allison, D. P. Geerke, B. A. C. Horta, P. H. Hunenberger, S. Riniker, N. Schmid and W. F. van Gunsteren, J. Comput. Chem., 2012, 33, 340–353 CrossRef CAS PubMed.
- R. Salomon-Ferrer, D. A. Case and R. C. Walker, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 198–210 CrossRef CAS.
- J. A. Rackers, M. L. Laury, C. Lu, Z. Wang, L. Lagardère, J.-P. Piquemal, P. Ren and J. W. Ponder, J. Comput. Chem., 2018 Search PubMed , in preparation.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kale and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef CAS PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Pall, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- R. Salomon-Ferrer, A. W. Gotz, D. Poole, S. Le Grand and R. C. Walker, J. Chem. Theory Comput., 2013, 9, 3878–3888 CrossRef CAS PubMed.
- W. Smith and I. T. Todorov, Mol. Simul., 2006, 32, 935–943 CrossRef CAS.
- C. Kobayashi, J. Jung, Y. Matsunaga, T. Mori, T. Ando, K. Tamura, M. Kamiya and Y. Sugita, J. Comput. Chem., 2017, 38, 2193–2206 CrossRef CAS PubMed.
- K. J. Bowers, E. Chow, H. Xu, R. O. Dror, M. P. Eastwood, B. A. Gregersen, J. L. Klepeis, I. Kolossvary, M. A. Moraes, F. D. Sacerdoti, J. K. Salmon, Y. Shan and D. E. Shaw, Scalable Algorithms for Molecular Dynamics Simulations on Commodity Clusters, Proceedings of the 2006 ACM/IEEE Conference on Supercomputing, New York, NY, USA, 2006 Search PubMed.
- D. E. Shaw, R. O. Dror, J. K. Salmon, J. P. Grossman, K. M. Mackenzie, J. A. Bank, C. Young, M. M. Deneroff, B. Batson, K. J. Bowers, E. Chow, M. P. Eastwood, D. J. Ierardi, J. L. Klepeis, J. S. Kuskin, R. H. Larson, K. Lindorff-Larsen, P. Maragakis, M. A. Moraes, S. Piana, Y. Shan and B. Towles, Millisecond-scale Molecular Dynamics Simulations on Anton, Proceedings of the Conference on High Performance Computing Networking, Storage and Analysis, New York, NY, USA, 2009, pp 39:1–39:11 Search PubMed.
- N. Gresh, P. Claverie and A. Pullman, Theor. Chim. Acta, 1984, 66, 1–20 CrossRef CAS.
- A. Stone, The Theory of Intermolcular Forces, Oxford Scholarship, 2013 Search PubMed.
- W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, J. Am. Chem. Soc., 1996, 118, 2309 CrossRef CAS.
- M. S. Gordon, M. A. Freitag, P. Bandyopadhyay, J. H. Jensen, V. Kairys and W. J. Stevens, J. Phys. Chem. A, 2001, 105, 293–307 CrossRef CAS.
- O. Engkvist, P.-O. Atrand and G. Karlstromm, Chem. Rev., 2000, 100, 4087–4108 CrossRef CAS PubMed.
- M. S. Gordon, L. Slipchenko, H. Li and J. H. Jensen, in Chapter 10 The Effective Fragment Potential: A General Method for Predicting Intermolecular Interactions, ed. D. Spellmeyer and R. Wheeler, Annual Reports in Computational Chemistry Supplement C, Elsevier, 2007, vol. 3, pp. 177–193 Search PubMed.
- P. Ren and J. W. Ponder, J. Phys. Chem. B, 2003, 107, 5933–5947 CrossRef CAS.
- G. Lamoureux and B. Roux, J. Chem. Phys., 2003, 119, 3025–3039 CrossRef CAS.
- N. Gresh, G. A. Cisneros, T. A. Darden and J.-P. Piquemal, J. Chem. Theory Comput., 2007, 3, 1960–1986 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chem. Theory Comput., 2007, 3, 1877 CrossRef CAS PubMed.
- Y. Shi, P. Ren, M. Schnieders and J.-P. Piquemal, Reviews in Computational Chemistry, John Wiley and Sons, Inc, 2015, vol. 28, pp. 51–86 Search PubMed.
- N. Gresh, K. E. Hage, E. Goldwaser, B. de Courcy, R. Chaudret, D. Perahia, C. Narth, L. Lagardère, F. Lipparini and J.-P. Piquemal, in Quantum Modeling of Complex Molecular Systems, ed. J.-L. Rivail, M. Ruiz-Lopez and X. Assfeld, Springer International Publishing, Cham, 2015, pp. 1–49 Search PubMed.
- J.-P. Piquemal and G. A. Cisneros, Many-Body Effects and Electrostatics in Biomolecules, Pan Standford, 2016, pp. 269–299 Search PubMed.
- W. Jiang, D. J. Hardy, J. C. Phillips, A. D. MacKerell, K. Schulten and B. Roux, J. Phys. Chem. Lett., 2011, 2, 87–92 CrossRef CAS PubMed.
- J. E. Stone, J. C. Phillips, P. L. Freddolino, D. J. Hardy, L. G. Trabuco and K. Schulten, J. Comput. Chem., 2007, 28, 2618–2640 CrossRef CAS PubMed.
- S. L. Grand, A. W. Gotz and R. C. Walker, Comput. Phys. Commun., 2013, 184, 374–380 CrossRef.
- M. Harger, D. Li, Z. Wang, K. Dalby, L. Lagardère, J.-P. Piquemal, J. Ponder and P. Ren, J. Comput. Chem., 2017, 38, 2047–2055 CrossRef CAS PubMed.
- P. Eastman, J. Swails, J. D. Chodera, R. T. McGibbon, Y. Zhao, K. A. Beauchamp, L.-P. Wang, A. C. Simmonett, M. P. Harrigan, C. D. Stern, R. P. Wiewiora, B. R. Brooks and V. S. Pande, PLoS Comput. Biol., 2017, 13, 1–17 Search PubMed.
- J. W. Ponder, C. Wu, P. Ren, V. S. Pande, J. D. Chodera, M. J. Schnieders, I. Haque, D. L. Mobley, D. S. Lambrecht, R. A. J. DiStasio, M. Head-Gordon, G. N. I. Clark, M. E. Johnson and T. Head-Gordon, J. Phys. Chem. B, 2007, 114, 2549–2564 CrossRef PubMed.
- J.-P. Piquemal, L. Perera, G. A. Cisneros, P. Ren, L. G. Pedersen and T. A. Darden, J. Chem. Phys., 2006, 125, 054511 CrossRef PubMed.
- K. J. Bowers, R. O. Dror and D. E. Shaw, J. Chem. Phys., 2006, 124, 184109 CrossRef PubMed.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Clarendon Press, New York, NY, USA, 1989 Search PubMed.
- L. Lagardère, F. Lipparini, E. Polack, B. Stamm, E. Cancès, M. Schnieders, P. Ren, Y. Maday and J. P. Piquemal, J. Chem. Theory Comput., 2015, 11, 2589–2599 CrossRef PubMed.
- F. Lipparini, L. Lagardère, B. Stamm, E. Cancès, M. Schnieders, P. Ren, Y. Maday and J.-P. Piquemal, J. Chem. Theory Comput., 2014, 10, 1638–1651 CrossRef CAS PubMed.
- F. Aviat, A. Levitt, B. Stamm, Y. Maday, P. Ren, J. W. Ponder, L. Lagardère and J.-P. Piquemal, J. Chem. Theory Comput., 2017, 13, 180–190 CrossRef CAS PubMed.
- F. Aviat, L. Lagardère and J.-P. Piquemal, J. Chem. Phys., 2017, 147, 161724 CrossRef PubMed.
- A. Klamt and G. Schuurmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- F. Lipparini, B. Stamm, E. Cancès, Y. Maday and B. Mennucci, J. Chem. Theory Comput., 2013, 9, 3637–3648 CrossRef CAS PubMed.
- F. Lipparini, L. Lagardère, C. Raynaud, B. Stamm, E. Cancès, B. Mennucci, M. Schnieders, P. Ren, Y. Maday and J.-P. Piquemal, J. Chem. Theory Comput., 2015, 11, 623–634 CrossRef CAS PubMed.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- A. Toukmaji, C. Sagui, J. Board and T. Darden, J. Chem. Phys., 2000, 113, 10913–10927 CrossRef CAS.
- C. Sagui, L. G. Pedersen and T. A. Darden, J. Chem. Phys., 2004, 120, 73–87 CrossRef CAS PubMed.
- C. Narth, L. Lagardère, É. Polack, N. Gresh, Q. Wang, D. R. Bell, J. A. Rackers, J. W. Ponder, P. Y. Ren and J.-P. Piquemal, J. Comput. Chem., 2016, 37, 494–506 CrossRef CAS PubMed.
- N. Li and S. Laizet, Cray User Group 2010 conference, Edinburgh, 2010 Search PubMed.
- M. Frigo and S. G. Johnson, Proc. IEEE, 2005, 93, 216–231 CrossRef , Special issue on “Program Generation, Optimization, and Platform Adaptation”.
- J. Kolafa, J. Comput. Chem., 2004, 25, 335–342 CrossRef CAS PubMed.
- M. Tuckerman, B. J. Berne and G. J. Martyna, J. Chem. Phys., 1992, 97, 1990–2001 CrossRef CAS.
- J. Wang, P. Cieplak, Q. Cai, M.-J. Hsieh, J. Wang, Y. Duan and R. Luo, J. Phys. Chem. B, 2012, 116, 7999–8008 CrossRef CAS PubMed.
- Y. Shi, Z. Xia, J. Zhang, R. Best, C. Wu, J. W. Ponder and P. Ren, J. Chem. Theory Comput., 2013, 9, 4046–4063 CrossRef CAS PubMed.
- A. Marjolin, C. Gourlaouen, C. Clavaguéra, P. Y. Ren, J. C. Wu, N. Gresh, J.-P. Dognon and J.-P. Piquemal, Theor. Chem. Acc., 2012, 131, 1198 CrossRef.
- A. Marjolin, C. Gourlaouen, C. Clavaguéra, P. Y. Ren, J.-P. Piquemal and J.-P. Dognon, J. Mol. Model., 2014, 20, 2471 CrossRef PubMed.
- T. A. Halgren, J. Am. Chem. Soc., 1992, 114, 7827–7843 CrossRef CAS.
- Y. Shi, Z. Xia, J. Zhang, R. Best, C. Wu, J. W. Ponder and P. Ren, J. Chem. Theory Comput., 2013, 9, 4046–4063 CrossRef CAS PubMed.
- A.-P. Hynninen and M. F. Crowley, J. Comput. Chem., 2014, 35, 406–413 CrossRef CAS PubMed.
- F. Endres and S. Z. E. Abedin, Phys. Chem. Chem. Phys., 2006, 8, 2101–2116 RSC.
- R. P. Swatloski, S. K. Spear, J. D. Holbrey and R. D. Rogers, J. Am. Chem. Soc., 2002, 124, 4974–4975 CrossRef CAS PubMed.
- H. Zhang, J. Wu, J. Zhang and J. He, Macromolecules, 2005, 38, 8272–8277 CrossRef CAS.
- D. Li, M. Wang, J. Wu, Q. Zhang, Y. Luo, Z. Yu, Q. Meng and Z. Wu, Langmuir, 2009, 25, 4808–4814 CrossRef CAS PubMed.
- O. N. Starovoytov, H. Torabifard and G. A. Cisneros, J. Phys. Chem. B, 2014, 118, 7156–7166 CrossRef CAS PubMed.
- Y.-J. Tu, M. J. Allen and G. A. Cisneros, Phys. Chem. Chem. Phys., 2016, 18, 10323–30333 Search PubMed.
- H. Torabifard, L. Reed, M. T. Berry, J. E. Jein, E. Menke and G. Cisneros, J. Chem. Phys., 2017, 147, 161731 CrossRef PubMed.
- T. Yan, C. J. Burnham, M. G. D. Pópolo and G. A. Voth, J. Phys. Chem. B, 2004, 108, 11877–11881 CrossRef CAS.
- A. Bagno, F. D'Amico and G. Saielli, J. Mol. Liq., 2007, 131–132, 17–23 CrossRef CAS.
- O. Borodin and G. D. Smith, J. Phys. Chem. B, 2006, 110, 6279–6292 CrossRef CAS PubMed.
- V. V. Chaban and O. V. Prezhdo, Phys. Chem. Chem. Phys., 2011, 13, 19345–19354 RSC.
- C. H. Bennett, J. Comput. Phys., 1976, 22, 245–268 CrossRef.
- L. Zheng, M. Chen and W. Yang, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 20227–20232 CrossRef CAS PubMed.
- P. L. Freddolino, A. S. Arkhipov, S. B. Larson, A. McPherson and K. Schulten, Structure, 2006, 14, 437–449 CrossRef CAS PubMed.
- J. R. Perilla, B. C. Goh, C. K. Cassidy, B. Liu, R. C. Bernardi, T. Rudack, H. Yu, Z. Wu and K. Schulten, Current Opinion in Structural Biology, 2015, vol. 31, pp. 64–74, Theory and simulation/Macromolecular machines and assembliesTheory and simulation/Macromolecular machines and assemblies Search PubMed.
- E. G. Kratz, A. R. Walker, L. Lagardère, F. Lipparini, J.-P. Piquemal and G. Andrés Cisneros, J. Comput. Chem., 2016, 37, 1019–1029 CrossRef CAS PubMed.
- C. Curutchet, A. Muñoz-Losa, S. Monti, J. Kongsted, G. D. Scholes and B. Mennucci, J. Chem. Theory Comput., 2009, 5, 1838–1848 CrossRef CAS PubMed.
- S. Caprasecca, S. Jurinovich, L. Lagardère, B. Stamm and F. Lipparini, J. Chem. Theory Comput., 2015, 11, 694–704 CrossRef CAS PubMed.
- D. Loco, E. Polack, S. Caprasecca, L. Lagardère, F. Lipparini, J.-P. Piquemal and B. Mennucci, J. Chem. Theory Comput., 2016, 12, 3654–3661 CrossRef CAS PubMed.
- D. Loco, L. Lagardère, S. Caprasecca, F. Lipparini, B. Mennucci and J.-P. Piquemal, J. Chem. Theory Comput., 2017, 13, 4025–4033 CrossRef CAS PubMed.
- F. Lipparini, L. Lagardère, G. Scalmani, B. Stamm, E. Cancès, Y. Maday, J.-P. Piquemal, M. J. Frisch and B. Mennucci, J. Phys. Chem. Lett., 2014, 5, 953–958 CrossRef CAS PubMed.
- F. Lipparini, G. Scalmani, L. Lagardère, B. Stamm, E. Cancès, Y. Maday, J.-P. Piquemal, M. J. Frisch and B. Mennucci, J. Chem. Phys., 2014, 141, 184108 CrossRef PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093 CrossRef CAS PubMed.
- C. Cramer and D. Truhlar, Chem. Rev., 1999, 99, 2161–2200 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision A.03, Gaussian Inc, Wallingford CT, 2016 Search PubMed.
- R. M. Parrish, L. A. Burns, D. G. A. Smith, A. C. Simmonett, A. E. DePrince, E. G. Hohenstein, U. Bozkaya, A. Y. Sokolov, R. Di Remigio, R. M. Richard, J. F. Gonthier, A. M. James, H. R. McAlexander, A. Kumar, M. Saitow, X. Wang, B. P. Pritchard, P. Verma, H. F. Schaefer, K. Patkowski, R. A. King, E. F. Valeev, F. A. Evangelista, J. M. Turney, T. D. Crawford and C. D. Sherrill, J. Chem. Theory Comput., 2017, 13, 3185–3197 CrossRef CAS PubMed.
- M. Valiev, E. Bylaska, N. Govind, K. Kowalski, T. Straatsma, H. V. Dam, D. Wang, J. Nieplocha, E. Apra, T. Windus and W. de Jong, Comput. Phys. Commun., 2010, 181, 1477–1489 CrossRef CAS.
- M. Devereux, S. Raghunathan, D. G. Fedorov and M. Meuwly, J. Chem. Theory Comput., 2014, 10, 4229–4241 CrossRef CAS PubMed.
- Y. Zhang, T.-S. Lee and W. Yang, J. Chem. Phys., 1999, 110, 46–54 CrossRef CAS.
- J. M. Parks, H. Hu, A. J. Cohen and W. Yang, J. Chem. Phys., 2008, 129, 154106 CrossRef PubMed.
- L.-P. Wang, T. Head-Gordon, J. W. Ponder, P. Ren, J. D. Chodera, P. K. Eastman, T. J. Martinez and V. S. Pande, J. Phys. Chem. B, 2013, 117, 9956–9972 CrossRef CAS PubMed.
- A. M. N. Niklasson, P. Steneteg, A. Odell, N. Bock, M. Challacombe, C. J. Tymczak, E. Holmstrom, G. Zheng and V. Weber, J. Chem. Phys., 2009, 130, 214109 CrossRef PubMed.
- M. Müller and T. Aoki, arXiv preprint arXiv:1710.08616 2017.
- openacc, https://www.openacc.org, accessed: 2017-05-31.
- J. Huang, A. C. Simmonett, F. C. Pickard IV, A. D. MacKerell Jr and B. R. Brooks, J. Chem. Phys., 2017, 147, 161702 CrossRef PubMed.
- J.-P. Piquemal, G. A. Cisneros, P. Reinhardt, N. Gresh and T. A. Darden, J. Chem. Phys., 2006, 124, 104101 CrossRef PubMed.
- R. E. Duke, O. N. Starovoytov, J.-P. Piquemal and G. A. Cisneros, J. Chem. Theory Comput., 2014, 10, 1361–1365 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7sc04531j |
| This journal is © The Royal Society of Chemistry 2018 |