Open Access Article
Open Access ArticleUnderstanding light-driven H2 evolution through the electronic tuning of aminopyridine cobalt complexes†
Arnau
Call
 a,
Federico
Franco
a,
Noufal
Kandoth
a,
Federico
Franco
a,
Noufal
Kandoth
 a,
Sergio
Fernández
a,
Sergio
Fernández
 a,
María
González-Béjar
a,
María
González-Béjar
 b,
Julia
Pérez-Prieto
b,
Julia
Pérez-Prieto
 b,
Josep M.
Luis
b,
Josep M.
Luis
 c and
Julio
Lloret-Fillol
c and
Julio
Lloret-Fillol
 *ad
*ad
aInstitute of Chemical Research of Catalonia (ICIQ), The Barcelona Institute of Science and Technology, Avinguda Països Catalans 16, 43007 Tarragona, Spain. E-mail: jlloret@iciq.es
bInstituto de Ciencia Molecular (ICMol), Universidad de Valencia, C/Catedrático José Beltrán 2, Paterna, E46980 Valencia, Spain
cInstitut de Química Computacional i Catàlisi (IQCC), Departament de Química, Universitat de Girona, Campus Montilivi, E17071 Girona, Catalonia, Spain
dCatalan Institution for Research and Advanced Studies (ICREA), Passeig Lluïs Companys, 23, 08010, Barcelona, Spain
First published on 19th December 2017
Abstract
A new family of cobalt complexes with the general formula [CoII(OTf)2(Y,XPyMetacn)] (1R, Y,XPyMetacn = 1-[(4-X-3,5-Y-2-pyridyl)methyl]-4,7-dimethyl-1,4,7-triazacyclononane, (X = CN (1CN), CO2Et (1CO2Et), Cl (1Cl), H (1H), NMe2 (1NMe2)) where (Y = H, and X = OMe when Y = Me (1DMM)) is reported. We found that the electronic tuning of the Y,XPyMetacn ligand not only has an impact on the electronic and structural properties of the metal center, but also allows for a systematic water-reduction-catalytic control. In particular, the increase of the electron-withdrawing character of the pyridine moiety promotes a 20-fold enhancement of the catalytic outcome. By UV-Vis spectroscopy, luminescence quenching studies and Transient Absorption Spectroscopy (TAS), we have studied the direct reaction of the photogenerated [IrIII(ppy)2(bpy˙−)] (PSIr) species to form the elusive CoI intermediates. In particular, our attention is focused on the effect of the ligand architecture in this elemental step of the catalytic mechanism. Finally, kinetic isotopic experiments together with DFT calculations provide complementary information about the rate-determining step of the catalytic cycle.
Introduction
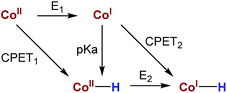
Hydrogen production by artificial photosynthesis is one of the most promising technologies to provide a clean and sustainable carbon-free fuel and feedstock for innumerable chemical processes.1 Better understanding of the mechanisms for H2 evolution is needed to develop more efficient catalysts. In this regard, a plethora of molecular catalysts based on Mo, Fe, Co and Ni have been studied as model systems.2 However, the challenging characterization of the key intermediates and the intrinsic complexity of the catalytic mechanisms enormously hinders their elucidation.3 In this regard, aminopyridine cobalt complexes are promising platforms to get insights into the elemental steps of the H2 evolution mechanism.The commonly proposed mechanism for water reduction catalysed by aminopyridine cobalt complexes involves the formation of a low oxidation state (presumably CoI), followed by protonation. Further reduction and protonation steps are invoked to induce the H–H bond formation (Scheme 1).4 However, it is not well understood how CoII/I reduction potential and cobalt hydride pKa values actually affect the overall reaction rate.5 On the other hand, although many studies have been focused on the detection of the short-lived CoI species,4b,d,6 to the best of our knowledge the direct reaction of CoII complexes with a reduced state of the photosensitizer still remains undefined.7 Likewise, the influence of the electronic effects of the ligand on the overall catalytic rate of the process is not fully understood.4b,c
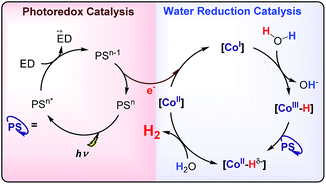 | ||
| Scheme 1 Commonly proposed mechanism for light-driven water reduction by aminopyridine cobalt complexes. | ||
Electronic effects have often been explored to gain insight into the hydrogen evolution catalytic mechanisms (Fig. 1).5,8 However, the studies are limited by the capacity of ligand modification, and the stability or activity of the water reduction catalysts under study. In many cases, this restricts or even leads to contradictory conclusions. For instance, for the [Co(R-PY5Me2)(H2O)](OTf)2 series (R = p-CF3 (2), p-H (3), p-NMe2 (4)), the photo- and electrocatalytic activity for H2 evolution was enhanced by introducing the electron withdrawing CF3 group.9 In contrast, for complexes [Co(bpy(Py-R)2Me)(X)(Y)](OTf) (R = p-CF3 (5), p-H (6), X, Y = CH3CN or OTf) and [Co((bpy)2PyMe-R(OTf))](OTf) (R = p-CF3 (7), p-H (8)), the introduction of a CF3 group led to a lower catalytic activity.10 In the case of cobalt corroles (H, F, Cl and Br, (9–12)) the decrease of the electron density over the metal centre induces an increase of the electrocatalytic activity.11
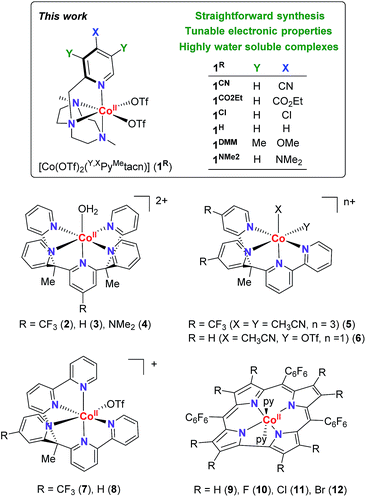 | ||
| Fig. 1 (Top) Cobalt complexes developed for this study. (Bottom) Selected cobalt water reduction catalysts where electronic effects have been reported in literature. | ||
With the aim to shed light on the key factors controlling the photocatalytic water reduction activity, we have developed a new family of well-defined cobalt complexes that are highly active in light-driven water reduction and whose electronic features can be tuned. To this end, we explored the cobalt complexes obtained from the readily available 1-[(4-X-3,5-Y-2-pyridyl)methyl]-4,7-dimethyl-1,4,7-triazacyclononane (Y,XPyMetacn) ligand family. In addition, we previously found that similar coordination complexes are water stable under reductive conditions and highly chelating.7,12 The electronic properties of the Y,XPyMetacn ligand are easily and systematically tuned by the substitution at the γ- (X: CN (1CN), CO2Et (1CO2Et), Cl (1Cl), H (1H), NMe2 (1NMe2)) and β-positions (X: OMe when Y: Me (1DMM)) of the pyridine (Scheme 2).12d
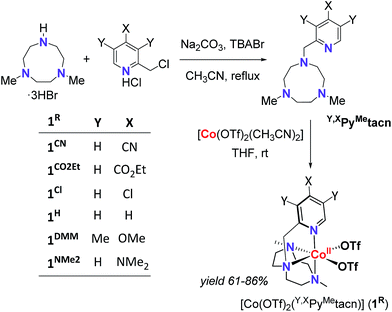 | ||
| Scheme 2 General scheme for the straightforward preparation of ligands and complexes studied herein. | ||
Herein, we report the synthesis, characterisation and photocatalytic water reduction activity of this new family of cobalt complexes with the general formula [CoII(OTf)2(Y,XPyMetacn)]. We present a detailed mechanistic study to elucidate the key steps of the H2 formation and how the electronic nature of the ligand affects the total reaction rate. We also study the role of [IrIII(ppy)2(bpy)]PF6 (PSIr+), its reduction to [IrIII(ppy)2(bpy˙−)] (PSIr) and the reaction of the latter with the cobalt catalysts to form CoI species by steady state and transient absorption kinetics and fluorescence quenching experiments. Deuterium labelling and computational modelling also provided complementary information about the rate-determining step of the catalytic cycle. Altogether, these data allow for the rationalisation of the light-driven H2 evolution mechanism by 1R catalysts in terms of the electronic effects. We envision that the provided information will be valuable to design future generations of water reduction catalysts.
Results and discussion
Synthesis and characterization
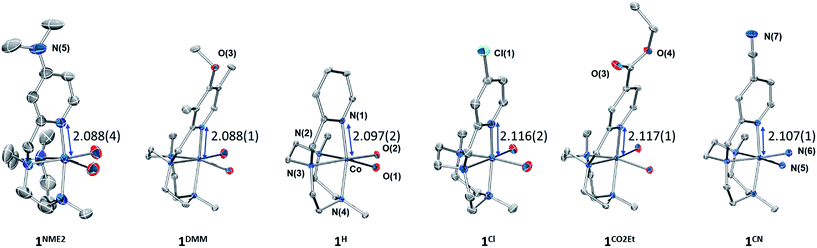
The Y,XPyMetacn (X ≠ CN) ligands were synthesised according to the literature (Scheme 2)12b,d and the H,CNPyMetacn ligand was obtained following an equivalent synthesis (see ESI Section 4.1†). An equimolar reaction of Y,XPyMetacn with [CoII(OTf)2(MeCN)2] gave six well-defined CoII complexes (1R) as crystalline materials in goods yields (61–86%). All complexes were fully characterized by UV-Vis absorption spectroscopy, ESI-MS, FT-IR, cyclic voltammetry, elemental analysis, 1H-NMR and single crystal X-ray diffraction crystallography (see ESI Section 4† for details). The 1H-NMR spectra window for 1R complexes ranged from −14 to 240 ppm and followed the Curie's law, which is in agreement with a high spin (S = 3/2) d7 CoII paramagnetic species. A down-shift of the α-proton of the pyridine, while increasing the electron withdrawing character of the ligand, clearly indicates the ligand influence in the physical properties of the complex (see ESI Section 4.2.2†).The solid-state structures of the synthesised cobalt complexes show slightly distorted octahedral coordination geometries for the CoII centre with four coordination sites occupied by the three N atoms of the tacn moiety and the N atom of the pyridine (Fig. 2), respectively, being isostructural to the previously reported equivalent FeII complexes.12d The Co–N bond lengths ranges from 2.0 to 2.2 Å, matching well with reported S = 3/2 CoII complexes.10a,13 The electronic properties of the substituted pyridine are reflected in a systematic modification of the CoII coordinative environment. For instance, the Co–Npy bond length (d(Co–Npy)) becomes smaller upon increasing the electron-donating character of the substituent (Fig. 2, Tables S1–S4†).
Both, X-ray diffraction and paramagnetic 1H-NMR data clearly show that the nature of the pyridine substituents significantly alters the Py–cobalt interaction in a systematic manner.
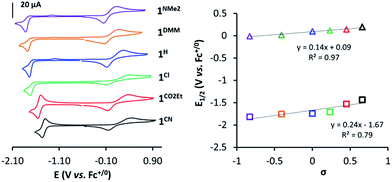
In a similar manner, the E1/2(CoII/I) values provide a good linearity in the Hammett plot (E1/2(CoII/I) vs. σ (Fig. 3)), and an overall anodic shift of ∼380 mV from 1NMe2 to 1CN in the series (Table 1) is observed. Electron-withdrawing groups at the para position of pyridine lead to reversible CoII/I waves, providing experimental E1/2(CoII/I) values of −1.53 V and −1.44 V (vs. Fc+/0) for 1CO2Et and 1CN, respectively. In contrast, in the case of 1Cl, 1H, 1DMM and 1NMe2, the CoII/I reduction appears as an irreversible peak at 0.1 V s−1, with a small oxidative peak occurring at ca. 550 mV more positive. However, reversibility of CoII/I wave is found at higher scan rates (Fig. S14–S17†). A linear dependence of the CoII/I peak current (ip) with the square root of the scan rate for all the 1R complexes is indicative of a diffusion-controlled reduction process (Fig. S14–S19†).
| Complex | E 1/2 (CoIII/II) (V) | E 1/2 (CoII/I) (V) | H2 (mmol) | Ratee (mmol H2 h−1) | Φ (%) |
|---|---|---|---|---|---|
a
E
1/2
vs. Fc+/0.
b At v = 50 V s−1.
c At v = 20 V s−1.
d At v = 10 V s−1.
e Measured before 10% H2 formed. Experimental conditions: 1R (50 μM), PSIr (150 μM) in CH3CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Et3N (4 Et3N (4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6:0.2 mL), irradiation (λ = 447 nm) at 25 °C.
f Reduction potential of the iridium photosensitizer (PSIr+/0) vs. Fc+/0 under catalytic conditions.
g Calculated as Φ = 2× n(H2)/(n(photons)) × 100. 6:0.2 mL), irradiation (λ = 447 nm) at 25 °C.
f Reduction potential of the iridium photosensitizer (PSIr+/0) vs. Fc+/0 under catalytic conditions.
g Calculated as Φ = 2× n(H2)/(n(photons)) × 100.
|
|||||
| 1NMe2 | −0.01 | −1.82b | 0.013 ± 0.002 | 0.025 ± 0.002 | 0.7 ± 0.1 |
| 1DMM | +0.02 | −1.76c | 0.018 ± 0.001 | 0.071 ± 0.003 | 1.9 ± 0.2 |
| 1H | +0.10 | −1.74b | 0.042 ± 0.002 | 0.137 ± 0.002 | 3.7 ± 0.4 |
| 1Cl | +0.12 | −1.71d | 0.051 ± 0.005 | 0.170 ± 0.009 | 4.6 ± 0.5 |
| 1CO2Et | +0.14 | −1.53 | 0.25 ± 0.01 | 0.356 ± 0.007 | 9.7 ± 1.0 |
| 1CN | +0.20 | −1.44 | 0.21 ± 0.01 | 0.336 ± 0.001 | 9.1 ± 0.9 |
| PSIr+/0 | −1.77f | ||||
Photocatalytic water reduction
Light-driven H2 evolution studies were performed to explore the influence of the ligand substitution on the catalytic activity of 1R complexes. We employed [IrIII(ppy)2(bpy)](PF6) (PSIr+) as photosensitiser and Et3N as sacrificial electron donor in MeCN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O (4
H2O (4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6) solvent mixture to guarantee the solubility of all components and irradiated at λ = 447 ± 20 nm (T = 25 °C). The gas evolution was monitored and H2 quantified by gas-chromatography (GC-TCD). Control experiments showed that all components are necessary for H2 formation and only a negligible amount of H2 was detected using [CoII(OTf)2(MeCN)2] as catalyst. The amount of H2 produced and the rate were unaffected in Hg0 poisoning experiments (1000 eq., see Fig. S20†), suggesting molecular catalysis,15 in concordance with the absence of induction time.
6) solvent mixture to guarantee the solubility of all components and irradiated at λ = 447 ± 20 nm (T = 25 °C). The gas evolution was monitored and H2 quantified by gas-chromatography (GC-TCD). Control experiments showed that all components are necessary for H2 formation and only a negligible amount of H2 was detected using [CoII(OTf)2(MeCN)2] as catalyst. The amount of H2 produced and the rate were unaffected in Hg0 poisoning experiments (1000 eq., see Fig. S20†), suggesting molecular catalysis,15 in concordance with the absence of induction time.
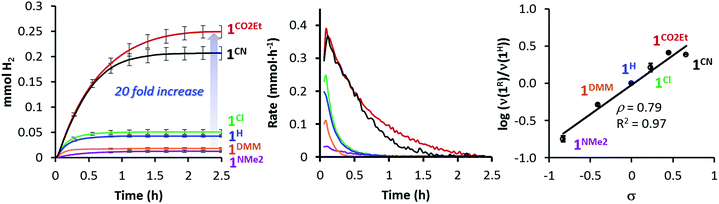
All 1R catalysts were active for the photo-induced hydrogen evolution but highly dependent on the substituent at the pyridine, following the order 1NMe2 < 1DMM < 1H < 1Cl < 1CO2Et ∼ 1CN. Indeed, the catalytic rate increases with the electron-withdrawing character of the ligand, in agreement with the E1/2(CoII/I) value (Table 1). Under standard conditions, the catalytic rate for the most active catalyst, 1CO2Et, was about 14-fold higher than 1NMe2 (the least active in the series), producing around 20 times more H2 (initial rate (νi) is 0.356 vs. 0.025 mmol h−1 and 6.1 vs. 0.3 mL H2, respectively) (Table 1, Fig. 4 left/middle). Interestingly, the hydrogen evolution rate (log(νi(1R)/νi(1H)) correlates very well with the sigma Hammett parameters (Fig. 4 right), but also with the redox E1/2(CoII/I) values (Fig. S21†). We have also calculated quantum yields for the photocatalytic water reduction, (Φ, based on two photons absorbed per produced H2 molecule), improving from 0.7% to 9.7% in the series from 1NMe2 to 1CO2Et (see Table 1).
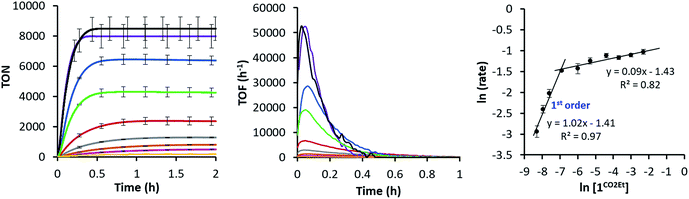
Since the 1CO2Et is the most active complex of the series, next we optimised its catalytic activity versus catalyst concentration. A non-linear increase of the total amount of H2 produced was observed upon increasing the amount of catalyst from 0.25 to 100 μM (Fig. S22†). This is in agreement with previous studies on aminopyridine cobalt complexes.16 Under optimised conditions, we obtained a TON value of about 9000 and TOFmax > 52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 h−1 at 0.25 μM catalyst (Fig. 5). To the best of our knowledge, the TOFmax value for 1CO2Et is higher than the highest reported to date for light-driven H2 evolution catalysts based on polypyridyl ligands.17 Among the latter, a TOFmax of 5880 h−1 and TON of ca. 33
000 h−1 at 0.25 μM catalyst (Fig. 5). To the best of our knowledge, the TOFmax value for 1CO2Et is higher than the highest reported to date for light-driven H2 evolution catalysts based on polypyridyl ligands.17 Among the latter, a TOFmax of 5880 h−1 and TON of ca. 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 were reported by Alberto et al. for the [CoBr(aPPy)]Br (aPPy = Di-2,2′-bipyridiyl-6-yl(pyridin-2-yl)methanol) complex after 70 h of irradiation.18 Nevertheless, we favour a TOF analysis rather that total TON measured on the plateau, since the TOF better represent electronic effects in the mechanism and the TON combines rate and stability. On the other hand, the water reduction quantum yield (Φ) for 1CO2Et (9.7% ± 1.0) is comparable to the highest reported value (7.5% ± 0.8)19 for similar Co complexes.19,20
300 were reported by Alberto et al. for the [CoBr(aPPy)]Br (aPPy = Di-2,2′-bipyridiyl-6-yl(pyridin-2-yl)methanol) complex after 70 h of irradiation.18 Nevertheless, we favour a TOF analysis rather that total TON measured on the plateau, since the TOF better represent electronic effects in the mechanism and the TON combines rate and stability. On the other hand, the water reduction quantum yield (Φ) for 1CO2Et (9.7% ± 1.0) is comparable to the highest reported value (7.5% ± 0.8)19 for similar Co complexes.19,20
Mechanistic investigations
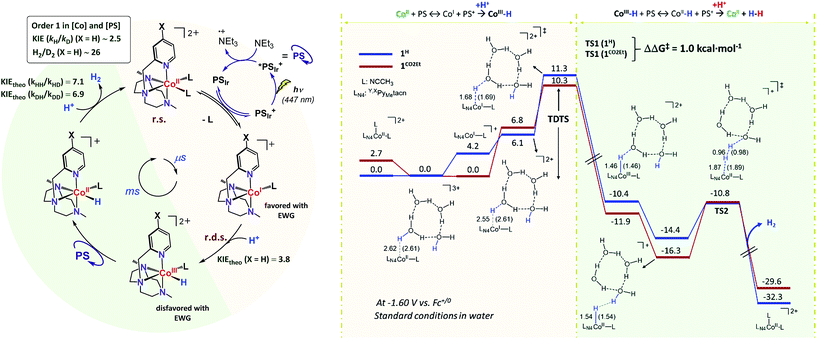
The intriguing electronic effects observed and the high catalytic activity of 1CO2Et and 1CN aimed us to study the mechanism in detail. Analysis of the catalytic experiments shows that the hydrogen evolution (at 10% of H2 formed) has a first-order dependence on 1CO2Et at concentrations below 2.5 μM (Fig. 5, right). Therefore, we propose that the catalytic mechanism is single site and follows a heterolytic H–H bond formation. At higher cobalt concentrations (in the range 2.5–100 μM) a saturation of the initial rate is observed. This might suggest that the catalytic cycle is controlled by the photon-flux or/and by the regeneration of the active CoI species, via CoII + PSIr ⇆ CoI + PSIr+ (PSIr = IrIII(ppy)2(bpy˙−)) pre-equilibrium. The latter possibility is further supported by the direct reaction of in situ formed [IrIII(ppy)2(bpy˙−)] with 1R. Subsequent reactivity studies have been performed under relevant conditions for catalysis.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CH3CN (4
CH3CN (4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6). The emission spectra and the lifetime decay of *PSIr+ are practically unchanged upon addition of 1CN aliquots (Fig. S25†) while undergo quenching with Et3N (Fig. S26A–C†). These results indicate that *PSIr+ is predominantly quenched by the sacrificial tertiary amine (Et3N). As a consequence, PSIr together with triethylamine radical cation are generated upon irradiation. Stern–Volmer quenching analysis for *PSIr+ with Et3N provided a linear fit for both the steady-state and time-resolved luminescence, with a quenching rate constant (kq) of 1.7 × 107 M−1 s−1 and 1.9 × 107 M−1 s−1, respectively (H2O
6). The emission spectra and the lifetime decay of *PSIr+ are practically unchanged upon addition of 1CN aliquots (Fig. S25†) while undergo quenching with Et3N (Fig. S26A–C†). These results indicate that *PSIr+ is predominantly quenched by the sacrificial tertiary amine (Et3N). As a consequence, PSIr together with triethylamine radical cation are generated upon irradiation. Stern–Volmer quenching analysis for *PSIr+ with Et3N provided a linear fit for both the steady-state and time-resolved luminescence, with a quenching rate constant (kq) of 1.7 × 107 M−1 s−1 and 1.9 × 107 M−1 s−1, respectively (H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CH3CN (4
CH3CN (4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6), see ESI Table S6 and Fig. S26D†).21
6), see ESI Table S6 and Fig. S26D†).21
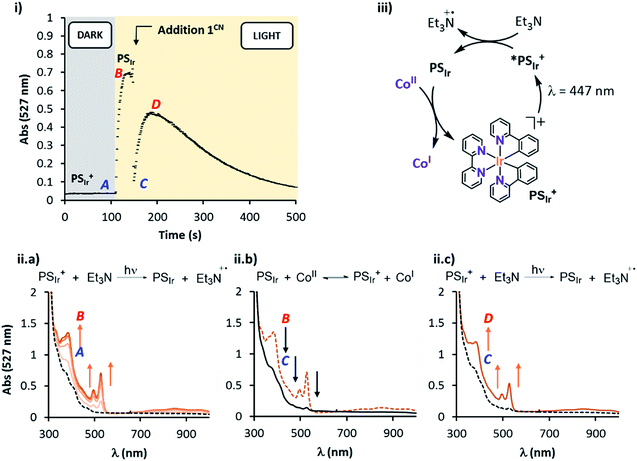
Study of the PSIr formation and their reactivity with 1R in pure CH3CN. The study in pure acetonitrile allows for a model study of the reactivity between 1R and the reduced form of the photoredox catalyst. This is the first step of the catalytic cycle, which is difficult to study otherwise. Optimum conditions to study the formation of PSIr consist in the irradiation (λ = 447 nm) of a solution containing PSIr+ (0.1 mM) and Et3N (1000 eq.) in anhydrous degassed CH3CN under N2 atmosphere at −20 °C, which produced the appearance of three new UV-Vis bands at 385, 495 and 523 nm and a broad band centred at 850 nm consistent with an electron delocalized over the bpy ligand (Fig. 6, iia). These new bands are ascribed to the formation of PSIr.7 The UV-Vis spectra recorded during irradiation (ESI Section 3† for the Experimental setup) showed a fast formation of PSIr up to a plateau (ca. 30 s), followed by a slow decay (Fig. S31†).22 Interestingly, the addition of 1CN (0.2 eq., 20 μM) at the maximized PSIr absorbance (527 nm), led to an instantaneous disappearance (mixing time) of the PSIr spectral features. This is in agreement with a fast electron transfer from the PSIr to 1CN that leads to the formation of a new reduced cobalt species (presumably CoI), regenerating PSIr+ (Fig. 6 (i and iib)). Interestingly, the amount of PSIr vanished is proportional to the amount of 1CN added. PSIr was fully consumed for a [1CN] equal or higher than 15 μM. Considering an ideal 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometric reaction between PSIr and 1CN, the estimated in situ photogenerated PSIr is ca. 15 μM, the 15% of the initial [PSIr+] (Fig. S27 and S28†). Further irradiation partially recovered the UV-Vis bands belonging to PSIr (Fig. 6 (iic)). Analogous studies with different 1R complexes showed that the extension of the PSIr decay depends on the reduction potential of 1R, following the same trend observed for the photocatalytic H2 evolution 1CN – 1CO2Et > 1Cl > 1H > 1DMM > 1NMe2 (Fig. S29 and S30†).23
1 stoichiometric reaction between PSIr and 1CN, the estimated in situ photogenerated PSIr is ca. 15 μM, the 15% of the initial [PSIr+] (Fig. S27 and S28†). Further irradiation partially recovered the UV-Vis bands belonging to PSIr (Fig. 6 (iic)). Analogous studies with different 1R complexes showed that the extension of the PSIr decay depends on the reduction potential of 1R, following the same trend observed for the photocatalytic H2 evolution 1CN – 1CO2Et > 1Cl > 1H > 1DMM > 1NMe2 (Fig. S29 and S30†).23
In addition, changes in absorbance of PSIr at 527 nm and the difference between E1/2(CoII/I) and E1/2(Ir+/0) (−1.76 V vs. Fc+/0) reduction potential follows the Nernst equation (eqn (S3) and (S4), see ESI† for details), reproducing well the sigmoidal theoretical curve (Fig. 7). It is important to notice that a similar dependence is observed with H2 evolution initial rates measured under the catalytic conditions. These data suggest that the H2 evolution rate, catalysed by the 1R complexes, is mainly controlled by the redox potential of the CoII/I event.
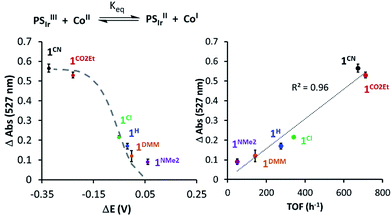 | ||
| Fig. 7 (Left) The 527 nm absorbance decay upon addition of 1Rvs. Δ(E1/2(PSIr+/PSIr) − E1/2(CoII/I)). (Right) 527 nm absorbance of PSIr decay upon addition of 1Rvs. TOF (h−1) (initial rate at 10% conversion of H2 evolution). The dashed grey line refers to the theoretical values predicted from Nernst equation (see Section ESI 6.1†). | ||
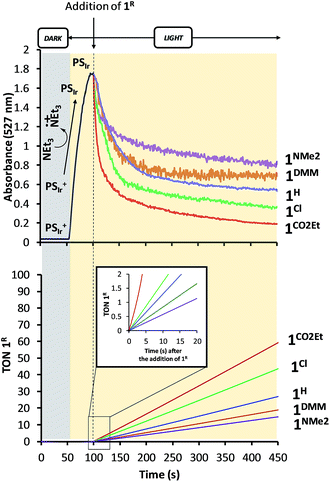
Study of the formation of PSIr and reactivity with 1R under catalytic conditions. Similar absorption kinetics experiments were carried out by using MeCN
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O (2
H2O (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) mixture as solvent. The reactivity of the PSIr with 1R complexes under catalytic conditions is similar to that observed in dry CH3CN. We monitored at the same time UV-Vis spectral changes and the amount of evolved H2 during the reaction. In a typical experiment, 0.1 eq. of 1R catalysts were added to a MeCN
3) mixture as solvent. The reactivity of the PSIr with 1R complexes under catalytic conditions is similar to that observed in dry CH3CN. We monitored at the same time UV-Vis spectral changes and the amount of evolved H2 during the reaction. In a typical experiment, 0.1 eq. of 1R catalysts were added to a MeCN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O (0.8
H2O (0.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.2 mL) solution containing PSIr+ (0.25 mM) and Et3N (100 mM) under N2 atmosphere at 25 °C. In situ produced PSIr rapidly decayed upon the addition of 1R under continuous light irradiation (λ = 447 nm).24 The extent and rate of such decay depends on the CoII/I redox potential of the added 1R catalyst, being faster for the more electron-poor 1R complexes (Fig. 7). The resulting order, 1CO2Et > 1Cl > 1H > 1DMM > 1NMe2, qualitatively reproduces well the rate for H2 formation and is fully consistent with the results in anhydrous CH3CN (Fig. 8). It is worth noting that no H2 was detected neither under irradiation of PSIr+ in absence of catalyst nor under dark conditions.
1.2 mL) solution containing PSIr+ (0.25 mM) and Et3N (100 mM) under N2 atmosphere at 25 °C. In situ produced PSIr rapidly decayed upon the addition of 1R under continuous light irradiation (λ = 447 nm).24 The extent and rate of such decay depends on the CoII/I redox potential of the added 1R catalyst, being faster for the more electron-poor 1R complexes (Fig. 7). The resulting order, 1CO2Et > 1Cl > 1H > 1DMM > 1NMe2, qualitatively reproduces well the rate for H2 formation and is fully consistent with the results in anhydrous CH3CN (Fig. 8). It is worth noting that no H2 was detected neither under irradiation of PSIr+ in absence of catalyst nor under dark conditions.
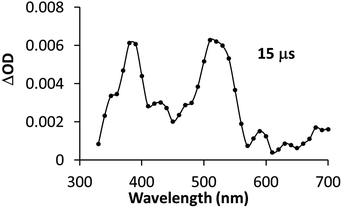
Study of the PSIr reactivity with 1CO2Et by transient absorption spectroscopy (TAS). Nanosecond transient absorption spectroscopy was used in order to achieve further mechanistic understanding on the PSIr formation and subsequent generation of CoI in neat acetonitrile.
First, the PSIr+ (50 μM) excitation (λex = 355 nm laser pulse) (see ESI† Experimental section) led to a strong characteristic emission centred at 600 nm and a positive band below 490 nm due to the formation of MLCT and LC PSIr+ triplet bands, both λmax (600, 470 nm) having a lifetime of ca. 350 ns (Fig. S32†). The differential absorption spectra and lifetime are in agreement with the reported excited triplet state (3PSIr+).25 The Et3N titration was followed at 600 nm and afforded a bimolecular quenching rate constant (kq) of 2.5 × 108 M−1 s−1 (Fig. S33, Table S7,† CH3CN as solvent). Moreover, we studied the changes in the transient absorption spectra of PSIr+ (50 μM), Et3N (20 mM) in presence of 1CO2Et (80 μM).
Interestingly, upon 355 nm laser excitation of a mixture containing PSIr+ (50 μM), Et3N (20 mM) and 1CO2Et (80 μM) in degassed CH3CN under Ar, a new transient species was detected (Fig. 9), presumably CoI,26 which has two absorption bands centred at 390 and 510 nm. The kinetic profile at 500 nm shows an estimate rise-time of ca. 1 μs for the generation of CoI species (Fig. S34†). Since the rate constant of the electron transfer from PSIr to CoII is in the order of few μs, we can rule out the latter as the rate-determining step of the catalytic cycle (a TOF = 14.4 s−1, corresponding to 70 ms per cycle, was obtained for 1CO2Et).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HD
HD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D2) analysis were carried out to better understand the protonation steps in the catalytic cycle (see Scheme 1, see Section ESI 7† for Experimental details). The on-line monitoring of the isotopic distribution can provide information not only about the rate-determining step but also about the hydrogen–hydrogen bond formation step. Nevertheless, a study of the formation rate of the different isotopomers (H2, HD and D2) and isotopic ratios has never been performed in the context of photocatalytic water reduction.
D2) analysis were carried out to better understand the protonation steps in the catalytic cycle (see Scheme 1, see Section ESI 7† for Experimental details). The on-line monitoring of the isotopic distribution can provide information not only about the rate-determining step but also about the hydrogen–hydrogen bond formation step. Nevertheless, a study of the formation rate of the different isotopomers (H2, HD and D2) and isotopic ratios has never been performed in the context of photocatalytic water reduction.
Studies were performed in H2O, D2O (99%) and H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D2O (1
D2O (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
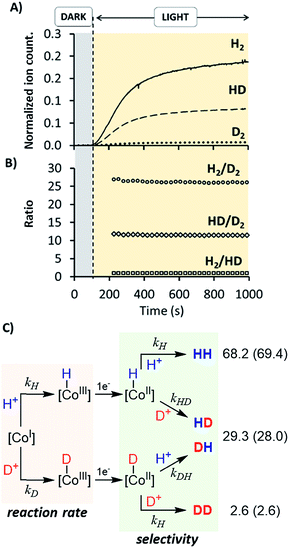
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) using 1H as catalyst (Fig. 10 and S35†). The KIEg (kH2O/kD2O) value, obtained by comparing the initial reactions rates in H2O vs. D2O (99.9%), was 2.5 (Fig. S36†). This suggests that the rate-determining step of the overall catalytic process could involve a formation of a X–H bond, such as the protonation of CoI or CoII–H intermediates, to give CoIII–H or hydrogen, respectively.27 On-line MS studies provided further insights into the identification of the specific products generated during the light-driven catalysed processes (Fig. 10).
1) using 1H as catalyst (Fig. 10 and S35†). The KIEg (kH2O/kD2O) value, obtained by comparing the initial reactions rates in H2O vs. D2O (99.9%), was 2.5 (Fig. S36†). This suggests that the rate-determining step of the overall catalytic process could involve a formation of a X–H bond, such as the protonation of CoI or CoII–H intermediates, to give CoIII–H or hydrogen, respectively.27 On-line MS studies provided further insights into the identification of the specific products generated during the light-driven catalysed processes (Fig. 10).
Irradiation of 1H in D2O resulted in a constant isotopic distribution of 0.5% H2, 9.1% HD and 90.4% D2 throughout all the experiment (Fig. S32†), which is an indication that the mechanism does not change over the reaction time. The HD and H2 measured should be attributed to the H2O content (1%) in D2O, which indicates a large isotopic selectivity. Likewise, when using a H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D2O (1
D2O (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) mixture the isotopic distribution was H2 (68.2 ± 0.2%) > HD (29.3 ± 0.2%) ≫ D2 (2.6 ± 0.2%) (Fig. 10), again unmodified during the reaction profile. The isotopic selectivity, H2vs. HD (KIESel(H2/HD)), is 2.3 (these two isotopomers are > 97% of the evolved gas), very close to the KIEg of 2.5. This suggests a coincidence in the rate-determining step and the reaction step that affects the H2/HD distribution. Moreover, the 26.6 ± 0.5 and 11.5 ± 0.1 values for the H2/D2 (KIESel(H2/D2)) and HD/D2 (KIESel(HD/D2)) ratios, respectively, are in agreement with two consecutive protonation events.
1) mixture the isotopic distribution was H2 (68.2 ± 0.2%) > HD (29.3 ± 0.2%) ≫ D2 (2.6 ± 0.2%) (Fig. 10), again unmodified during the reaction profile. The isotopic selectivity, H2vs. HD (KIESel(H2/HD)), is 2.3 (these two isotopomers are > 97% of the evolved gas), very close to the KIEg of 2.5. This suggests a coincidence in the rate-determining step and the reaction step that affects the H2/HD distribution. Moreover, the 26.6 ± 0.5 and 11.5 ± 0.1 values for the H2/D2 (KIESel(H2/D2)) and HD/D2 (KIESel(HD/D2)) ratios, respectively, are in agreement with two consecutive protonation events.
Presumably, the two consecutive events that control the isotopic distribution are the cobalt hydride bond formation and the hydrogen–hydrogen bond formation (see Fig. 10), but only the first affects the reaction rate. This is in agreement with the cobalt protonation as the rate-determining step of the hydrogen evolution.
Mechanistic discussion
To further evaluate the impact of the electronic effects on the CoII/I redox and the CoI protonation in the reaction rate we have computationally studied the thermodynamics of these elemental steps for all 1R complexes. We performed computational studies at the B3LYP-D3/cc-pVTZ//B3LYP-D3/6-31+G* level of theory, which previously gave good agreement in similar catalytic systems (see ESI† for Computational details).28 Theoretical E1/2(CoII/I) and E1/2(CoIII/II) values correlate within the expected errors for all 1R complexes (see Table 2). We also computed the CoIII–H pKa values, which are in the range from 8.4 to 15.4.| Complex | E 1 (V) | E 2 (V) | pKa | CPET1a,b (V) | CPET2a,b (V) |
|---|---|---|---|---|---|
| a vs. Fc+/0 b The CPET reduction potential values have been adjusted to pH = 11. | |||||
| 1NMe2 | −1.92 | −1.53 | 15.4 | −1.69 | −1.27 |
| 1DMM | −1.92 | −1.49 | 14.7 | −1.73 | −1.27 |
| 1H | −1.85 | −1.46 | 12.9 | −1.75 | −1.35 |
| 1Cl | −1.82 | −1.42 | 11.9 | −1.80 | −1.36 |
| 1COOEt | −1.74 | −1.44 | 11.5 | −1.80 | −1.40 |
| 1CN | −1.59 | −1.36 | 8.4 | −1.84 | −1.51 |
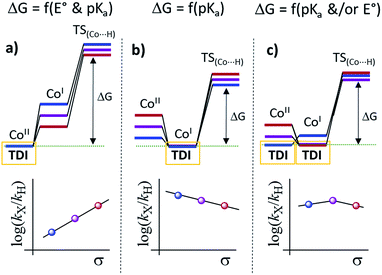
Our experimental studies discard that only the PSIr to CoII electron transfer step determines the rate of the overall process since it is much faster than the TOF. Therefore should be influence also by a second step. Indeed, the calculated difference of CoII/I reduction potential between 1NMe2 and 1CN is 330 mV, corresponding to −7.5 kcal mol−1 (expt. 380 mV, −8.9 kcal mol−1). These energies reflect the experimentally observed trend for catalysis, i.e. higher the E1/2(CoII/I) reduction potential faster the hydrogen evolution catalysis. However, taking into account only the E1/2(CoII/I) values, the reaction rate should be ca. 3 × 107 times faster for 1CN than 1NMe2 (considering the experimental E1/2(CoII/I), 3 × 106 considering the theoretical values). However, the experimental rate increase between 1NMe2 and 1CN is only about 20-fold (−1.8 kcal mol−1), approximately 6 orders of magnitude different. We can also rule out the CoI protonation to form CoIII–H as the only contribution to the rate law. The CoIII–H pKa values difference between 1NMe2 and 1CN corresponds to +9.5 kcal mol−1, which is opposite to the redox values. In this scenario and considering the Bell–Evans–Polanyi (BEP) principle and Marcus type analytical expressions (1–3) (see below), lower the pKa of CoIII–H species, slower the catalytic reaction rate.
Therefore, the energy barrier of the reaction either involves a stepwise CoII reduction followed by protonation (rate-determining step suggested by KIE), or a proton coupled electron transfer (CPET). However, based on thermodynamic data, BEP and eqn (1)–(3), we may discard both possible CPET, CoII → CoIII–H and CoI → CoII–H, as they are +3.5 and +5.5 kcal mol−1 less favourable for 1CN than for 1NMe2, respectively.29 Thus, neither CPET1 nor CPET2 processes can be involved in the rate-determining step.
We have also calculated the protonation barrier for CoI, in both cases 1H and 1CO2Et, being the ΔΔG‡ value 3.2 kcal mol−1 in favour of 1H, again opposite to the energy obtained from the experimental results (−0.8 kcal mol−1). Finally, we have considered the sum of the CoII/I reduction potential thermodynamics and the energy barrier for the CoI protonation. This is indeed the value of the total energy barrier if the production of CoI is an endergonic step (see Fig. 11). In this case, the difference between the 1H and 1CO2Et energy barriers is −1.0 kcal mol−1, which is in very good agreement with the experimental energy difference (−0.8 kcal mol−1). Calculated kinetic isotopic effects for this mechanism for 1H (3.8) qualitatively matches with the experimental KIEg (kH2O/kD2O) of 2.5. The KIEs values calculated starting from Co–H and Co–D, to give hydrogen, are 7.1 and 6.9, respectively, which are clearly much larger than the experimental KIEg (kH2O/kD2O). In addition, we have calculated the distribution of the isotopomers using the values obtained theoretically and considering the proposed mechanism (Fig. 11). Interestingly, the experimental and theoretical isotopic distributions matched perfectly (experimental [H2: 68.2, HD: 29.3, D2: 2.6] and Theoretical [H2: 69.1, HD: 28.3, D2 2.6]) (see Fig. S10c†).
At this point it is interesting to discuss this result within the context of the theoretical model developed by M. Koper and co.,30 which takes into account the role of the pH in the selectivity between the concerted proton–electron transfer (CPET) and sequential proton–electron (or electron-proton) transfer (SPET) pathways. The proposed theoretical model assumes an outer-sphere charge transfer mechanism and provides the following Marcus-type analytical expressions for the activation energies of the electron-transfer (ET), proton transfer (PT) and CPET steps.
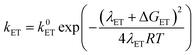 | (1) |
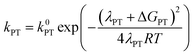 | (2) |
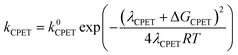 | (3) |
| λCPET = λET + λPT + 2ƛ | (4) |
Altogether, our results are in agreement with a sequential reduction-protonation mechanism (SEP), in which the CoI protonation, to give CoIII–H, determines the TOF-dependent transition state (TDTS).32 Furthermore, in the proposed catalytic cycle the TOF-determining intermediate (TDI) is dependent on the redox potentials of either the photosensitizer (E1/2(PSIr+/0)) and the starting CoII complex (E1/2(CoII/I)). In our case, from combined UV-Vis spectroscopic/H2 evolution monitoring studies, we have observed that the concentration of photosensitizer in the reduced form is very low. Therefore, the E1/2 redox potential of the photosensitizer should be used only as an estimation. Considering the Nernst equation and the concentration of the photosensitizer species in solution, we can roughly estimate that the redox potential of the PSIr+/0 couple is about 100–200 mV less reducing that the E1/2. Accordingly, the redox potential for CoII/I should be more reducing than the photosensitizer. The difference in redox potential between the CoII/I and photosensitize is directly translate in the hydrogen evolution reaction rate becoming faster with a more electron-withdrawing ligand. In other words, CoII is the TOF-determining intermediate and its reduction is an endergonic step that contributes to increase the total energy barrier (see Fig. 11). On the other hand, if the redox potential of the photosensitizer is more reducing (lower E(CoII/I) reduction potential)33 that redox potential of the CoII/I process, the rate could be only dependent on the CoI protonation, which is expected to be thermodynamically less feasible for more electron-withdrawing ligands (see Table 2). This simplified scenario may help to rationalize some of the different results in the field of light-driven water reduction (Fig. 12).
Conclusions
We have developed a new family of cobalt complexes active for water reduction, which allows for a systematic study of the catalytic activity as a function of the electronic properties of the metal centre. Within the series, a span of 380 mV for the E1/2(CoII/I) resulted in 20-fold increase of H2 evolution activity, by modification of the pyridine substituents (from the electron-donating –NMe2, to the electron-withdrawing –CN group). UV-Vis spectroscopy, Luminescence Quenching Studies and Transient Absorption Spectroscopy, allow to study the reaction of photogenerated [IrIII(ppy)2(bpy˙−)] (PSIr) species with the different CoII complexes to form the elusive CoI intermediates. Formation of the CoI is estimated to be in the order of μs, much faster that the catalytic rate. Kinetic isotopic experiments together with DFT calculations are consistent with: (i) the CoI protonation to form CoIII–H as the TOF-determining transition state (TDTS) of the catalytic cycle and (ii) CoII species as the TOF-determining intermediate (TDI). We propose that in the herein reported catalytic system (under basic conditions), the TDI depends on the redox potentials of both 1R metal complexes and photoredox catalysts. We postulate that these phenomena could be more general. Ongoing work in our group is tackling this problem. We envision that the reported mechanistic investigation will aid in the general understanding of the water reduction reaction, and will trigger the development of more active water reduction catalysts.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to thank the European Commission for the ERC-CG-2014-648304 (J. Ll.-F.) project and Spanish MINECO (CTQ2016-80038-R) project. The financial support from ICIQ Foundation and CELLEX Foundation through the CELLEX-ICIQ high throughput experimentation platform and the Starting Career Program is gratefully acknowledged. We also thank CERCA Programme (Generalitat de Catalunya); The MINECO is acknowledged for a FPU fellowship to A. C. (AP2012-6436) and ICIQ-IPMP program (F. F.) and Severo Ochoa Excellence Accreditation 2014–2018 (SEV-2013-0319). J. M. L. is grateful for financial support from the Spanish MINECO CTQ2014-52525-P and the Catalan DIUE 2014SGR931. J. P.-P. gratefully acknowledge CTQ2014-60174-P (partially co-financed with FEDER funds), Maria de Maeztu (MDM-2015-0538), (RyC contract to MGB) and Fundación Ramón Areces for financial support. We also thank Catexel for a generous gift of tritosyl-1,4,7-triazacyclononane.Notes and references
- (a) H. B. Gray, Nat. Chem., 2009, 1, 7 CrossRef CAS PubMed; (b) N. S. Lewis and D. G. Nocera, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15729 CrossRef CAS PubMed.
- (a) P. Du and R. Eisenberg, Energy Environ. Sci., 2012, 5, 6012 RSC; (b) J. R. McKone, S. C. Marinescu, B. S. Brunschwig, J. R. Winkler and H. B. Gray, Chem. Sci., 2014, 5, 865 RSC; (c) V. Artero, M. Chavarot-Kerlidou and M. Fontecave, Angew. Chem., Int. Ed., 2011, 50, 7238 CrossRef CAS PubMed.
- (a) A. Kahnt, K. Peuntinger, C. Dammann, T. Drewello, R. Hermann, S. Naumov, B. Abel and D. M. Guldi, J. Phys. Chem. A, 2014, 118, 4382 CrossRef CAS PubMed; (b) S. C. Marinescu, J. R. Winkler and H. B. Gray, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 15127–15131 CrossRef CAS PubMed; (c) D. Moonshiram, C. Gimbert-Surinach, A. Guda, A. Picon, C. S. Lehmann, X. Zhang, G. Doumy, A. M. March, J. Benet-Buchholz, A. Soldatov, A. Llobet and S. H. Southworth, J. Am. Chem. Soc., 2016, 138, 10586 CrossRef CAS PubMed; (d) D. C. Lacy, G. M. Roberts and J. C. Peters, J. Am. Chem. Soc., 2015, 137, 4860 CrossRef CAS PubMed; (e) A. Bhattacharjee, M. Chavarot-Kerlidou, E. S. Andreiadis, M. Fontecave, M. J. Field and V. Artero, Inorg. Chem., 2012, 51, 7087 CrossRef CAS PubMed.
- (a) N. Queyriaux, R. T. Jane, J. Massin, V. Artero and M. Chavarot-Kerlidou, Coord. Chem. Rev., 2015, 304–305, 3 CrossRef CAS PubMed; (b) W. K. Lo, C. E. Castillo, R. Gueret, J. Fortage, M. Rebarz, M. Sliwa, F. Thomas, C. J. McAdam, G. B. Jameson, D. A. McMorran, J. D. Crowley, M. N. Collomb and A. G. Blackman, Inorg. Chem., 2016, 55, 4564 CrossRef CAS PubMed; (c) B. Shan, T. Baine, X. A. Ma, X. Zhao and R. H. Schmehl, Inorg. Chem., 2013, 52, 4853 CrossRef CAS PubMed; (d) S. Varma, C. E. Castillo, T. Stoll, J. Fortage, A. G. Blackman, F. Molton, A. Deronzier and M. N. Collomb, Phys. Chem. Chem. Phys., 2013, 15, 17544 RSC.
- B. H. Solis and S. Hammes-Schiffer, J. Am. Chem. Soc., 2011, 133, 19036 CrossRef CAS PubMed.
- (a) A. Lewandowska-Andralojc, T. Baine, X. Zhao, J. T. Muckerman, E. Fujita and D. E. Polyansky, Inorg. Chem., 2015, 54, 4310 CrossRef CAS PubMed; (b) A. Rodenberg, M. Orazietti, B. Probst, C. Bachmann, R. Alberto, K. K. Baldridge and P. Hamm, Inorg. Chem., 2015, 54, 646 CrossRef CAS PubMed; (c) W. M. Singh, M. Mirmohades, R. T. Jane, T. A. White, L. Hammarstrom, A. Thapper, R. Lomoth and S. Ott, Chem. Commun., 2013, 49, 8638 RSC; (d) S. Mandal, S. Shikano, Y. Yamada, Y. M. Lee, W. Nam, A. Llobet and S. Fukuzumi, J. Am. Chem. Soc., 2013, 135, 15294 CrossRef CAS PubMed.
- A. Call, Z. Codolà, F. Acuña-Parés and J. Lloret-Fillol, Chem.–Eur. J., 2014, 20, 6171 CrossRef CAS PubMed.
- (a) P. Du, J. Schneider, G. Luo, W. W. Brennessel and R. Eisenberg, Inorg. Chem., 2009, 48, 4952 CrossRef CAS PubMed; (b) U. J. Kilgore, J. A. Roberts, D. H. Pool, A. M. Appel, M. P. Stewart, M. R. DuBois, W. G. Dougherty, W. S. Kassel, R. M. Bullock and D. L. DuBois, J. Am. Chem. Soc., 2011, 133, 5861 CrossRef CAS PubMed; (c) U. J. Kilgore, M. P. Stewart, M. L. Helm, W. G. Dougherty, W. S. Kassel, M. R. DuBois, D. L. DuBois and R. M. Bullock, Inorg. Chem., 2011, 50, 10908 CrossRef CAS PubMed; (d) D. L. DuBois, Inorg. Chem., 2014, 53, 3935 CrossRef CAS PubMed; (e) B. H. Solis, Y. Yu and S. Hammes-Schiffer, Inorg. Chem., 2013, 52, 6994 CrossRef CAS PubMed.
- Y. Sun, J. Sun, J. R. Long, P. Yang and C. J. Chang, Chem. Sci., 2013, 4, 118 RSC.
- (a) R. S. Khnayzer, V. S. Thoi, M. Nippe, A. E. King, J. W. Jurss, K. A. El Roz, J. R. Long, C. J. Chang and F. N. Castellano, Energy Environ. Sci., 2014, 7, 1477 RSC; (b) M. Nippe, R. S. Khnayzer, J. A. Panetier, D. Z. Zee, B. S. Olaiya, M. Head-Gordon, C. J. Chang, F. N. Castellano and J. R. Long, Chem. Sci., 2013, 4, 3934 RSC.
- A. Mahammed, B. Mondal, A. Rana, A. Dey and Z. Gross, Chem. Commun., 2014, 50, 2725 RSC.
- (a) J. Lloret-Fillol, Z. Codolà, I. Garcia-Bosch, L. Gómez, J. J. Pla and M. Costas, Nat. Chem., 2011, 3, 807 CrossRef PubMed; (b) I. Prat, D. Font, A. Company, K. Junge, X. Ribas, M. Beller and M. Costas, Adv. Synth. Catal., 2013, 355, 947 CrossRef CAS; (c) I. Garcia-Bosch, Z. Codola, I. Prat, X. Ribas, J. Lloret-Fillol and M. Costas, Chem.–Eur. J., 2012, 18, 13269 CrossRef CAS PubMed; (d) I. Prat, A. Company, T. Corona, T. Parella, X. Ribas and M. Costas, Inorg. Chem., 2013, 52, 9229 CrossRef CAS PubMed; (e) A. Company, L. Gomez, X. Fontrodona, X. Ribas and M. Costas, Chem.–Eur. J., 2008, 14, 5727 CrossRef CAS PubMed; (f) A. Company, L. Gómez, M. Güell, X. Ribas, J. M. Luis, J. Lawrence Que and M. Costas, J. Am. Chem. Soc., 2007, 129, 15766 CrossRef CAS PubMed.
- A. L. Ward, L. Elbaz, J. B. Kerr and J. Arnold, Inorg. Chem., 2012, 51, 4694–4706 CrossRef CAS PubMed.
- C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165 CrossRef CAS.
- V. Artero and M. Fontecave, Chem. Soc. Rev., 2013, 42, 2338 RSC.
- C. Bachmann, M. Guttentag, B. Spingler and R. Alberto, Inorg. Chem., 2013, 52, 6055 CrossRef CAS PubMed.
- (a) M. Guttentag, A. Rodenberg, C. Bachmann, A. Senn, P. Hamm and R. Alberto, Dalton Trans., 2013, 42, 334 RSC; (b) W. M. Singh, T. Baine, S. Kudo, S. Tian, X. A. Ma, H. Zhou, N. J. DeYonker, T. C. Pham, J. C. Bollinger, D. L. Baker, B. Yan, C. E. Webster and X. Zhao, Angew. Chem., Int. Ed., 2012, 51, 5941 CrossRef CAS PubMed; (c) E. Joliat, S. Schnidrig, B. Probst, C. Bachmann, B. Spingler, K. K. Baldridge, F. von Rohr, A. Schilling and R. Alberto, Dalton Trans., 2016, 45, 1737 RSC.
- C. Bachmann, B. Probst, M. Guttentag and R. Alberto, Chem. Commun., 2014, 50, 6737 RSC.
- R. S. Khnayzer, V. S. Thoi, M. Nippe, A. E. King, J. W. Jurss, K. A. El Roz, J. R. Long, C. J. Chang and F. N. Castellano, Energy Environ. Sci., 2014, 7, 1477 CAS.
- (a) J. W. Jurss, R. S. Khnayzer, J. A. Panetier, K. A. El Roz, E. M. Nichols, M. Head-Gordon, J. R. Long, F. N. Castellano and C. J. Chang, Chem. Sci., 2015, 6, 4954 RSC; (b) M. Nippe, R. S. Khnayzer, J. A. Panetier, D. Z. Zee, B. S. Olaiya, M. Head-Gordon, C. J. Chang, F. N. Castellano and J. R. Long, Chem. Sci., 2013, 4, 3934 RSC.
- (a) H. Lv, W. Guo, K. Wu, Z. Chen, J. Bacsa, D. G. Musaev, Y. V. Geletii, S. M. Lauinger, T. Lian and C. L. Hill, J. Am. Chem. Soc., 2014, 136, 14015 CrossRef CAS PubMed; (b) A. Kobayashi, S. Watanabe, M. Ebina, M. Yoshida and M. Kato, J. Photochem. Photobiol., A, 2017, 347, 9 CrossRef CAS; (c) Y.-J. Yuan, Z.-T. Yu, X.-J. Liu, J.-G. Cai, Z.-J. Guan and Z.-G. Zou, Sci. Rep., 2014, 4, 4045 CrossRef PubMed; (d) J. I. Goldsmith, W. R. Hudson, M. S. Lowry, T. H. Anderson and S. Bernhard, J. Am. Chem. Soc., 2005, 127, 7502 CrossRef CAS PubMed.
- D. Hollmann, F. Gartner, R. Ludwig, E. Barsch, H. Junge, M. Blug, S. Hoch, M. Beller and A. Bruckner, Angew. Chem., Int. Ed., 2011, 50, 10246 CrossRef CAS PubMed.
- A. Panagiotopoulos, K. Ladomenou, D. Sun, V. Artero and A. G. Coutsolelos, Dalton Trans., 2016, 45, 6732 RSC.
- (a) E. A. Plummer, J. W. Hofstraat and L. D. Cola, Dalton Trans., 2003, 2080 RSC; (b) Y. You and W. Nam, Chem. Soc. Rev., 2012, 41, 7061 RSC; (c) J. Zhao, W. Wu, J. Sun and S. Guo, Chem. Soc. Rev., 2013, 42, 5323 RSC.
- (a) S.-H. Wu, J.-W. Ling, S.-H. Lai, M.-J. Huang, C. H. Cheng and I.-C. Chen, J. Phys. Chem. A, 2010, 114, 10339 CrossRef CAS PubMed; (b) F. Garces, K. A. King and R. J. Watts, Inorg. Chem., 1988, 27, 3464 CrossRef CAS; (c) D. Hanss, J. C. Freys, G. r. Bernardinelli and O. S. Wenger, Eur. J. Inorg. Chem., 2009, 2009, 4850 CrossRef; (d) M. S. Lowry and S. Bernhard, Chem.–Eur. J., 2006, 12, 7970 CrossRef CAS PubMed.
- (a) A. Rodenberg, M. Orazietti, B. Probst, C. Bachmann, R. Alberto, K. K. Baldridge and P. Hamm, Inorg. Chem., 2015, 54, 646 CrossRef CAS PubMed; (b) M. Natali, ACS Catal., 2017, 7, 1330 CrossRef CAS; (c) C.-F. Leung, S.-M. Ng, C.-C. Ko, W.-L. Man, J. Wu, L. Chen and T.-C. Lau, Energy Environ. Sci., 2012, 5, 7903 RSC; (d) A. Neubauer, G. Grell, A. Friedrich, S. I. Bokarev, P. Schwarzbach, F. Gärtner, A.-E. Surkus, H. Junge, M. Beller, O. Kühn and S. Lochbrunner, J. Phys. Chem. Lett., 2014, 5, 1355 CrossRef CAS PubMed.
- S. Aoi, K. Mase, K. Ohkubo and S. Fukuzumi, Chem. Commun., 2015, 51, 15145 RSC.
- F. Acuña-Parés, Z. Codolà, M. Costas, J. M. Luis and J. Lloret-Fillol, Chem.–Eur. J., 2014, 20, 5696 CrossRef PubMed.
- M. Bourrez, R. Steinmetz, S. Ott, F. Gloaguen and L. Hammarström, Nat. Chem., 2015, 7, 140 CrossRef CAS PubMed.
- (a) A. J. Göttle and M. T. M. Koper, Chem. Sci., 2017, 8, 458 RSC; (b) M. T. M. Koper, Phys. Chem. Chem. Phys., 2013, 15, 1399 RSC.
- (a) B. Auer, A. V. Soudackov and S. Hammes-Schiffer, J. Phys. Chem. B, 2012, 116, 7695 CrossRef CAS PubMed; (b) S. Hammes-Schiffer, ChemPhysChem, 2002, 3, 33 CrossRef CAS PubMed; (c) S. Hammes-Schiffer and A. A. Stuchebrukhov, Chem. Rev., 2010, 110, 6939 CrossRef CAS PubMed.
- S. Kozuch and S. Shaik, Acc. Chem. Res., 2011, 44, 101 CrossRef CAS PubMed.
- The reduction redox potential is defined as the potential of a compound measured under standards conditions against a standard reference half-cell.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 1578284–1578289. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7sc04328g |
| This journal is © The Royal Society of Chemistry 2018 |