Dye-sensitized electron transfer from TiO₂ to oxidized triphenylamines that follows first-order kinetics

Abstract

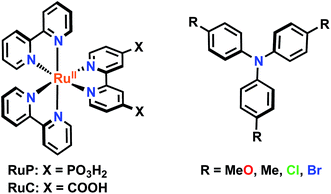
Two sensitizers, [Ru(bpy)₂(dcb)]²⁺ (RuC) and [Ru(bpy)₂(dpb)]²⁺ (RuP), where bpy is 2,2′-bipyridine, dcb is 4,4′-dicarboxylic acid-2,2′-bipyridine and dpb is 4,4′-diphosphonic acid-2,2′-bipyridine, were anchored to mesoporous TiO₂ thin films and utilized to sensitize the reaction of TiO₂ electrons with oxidized triphenylamines, TiO₂(e⁻) + TPA⁺ → TiO₂ + TPA, to visible light in CH₃CN electrolytes. A family of four symmetrically substituted triphenylamines (TPAs) with formal E^o(TPA^+/0) reduction potentials that spanned a 0.5 eV range was investigated. Surprisingly, the reaction followed first-order kinetics for two TPAs that provided the largest thermodynamic driving force. Such first-order reactivity indicates a strong Coulombic interaction between TPA⁺ and TiO₂ that enables the injected electron to tunnel back in one concerted step. The kinetics for the other TPA derivatives were non-exponential and were modelled with the Kohlrausch–William–Watts (KWW) function. A Perrin-like reaction sphere model is proposed to rationalize the kinetic data. The activation energies were the same for all of the TPAs, within experimental error. The average rate constants were found to increase with the thermodynamic driving force, consistent with electron transfer in the Marcus normal region.

---

Introduction

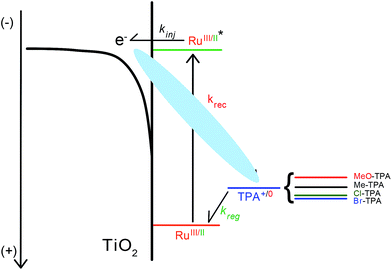
Motivation for the study of electron transfer reactions at semiconductor interfaces originates from both applications and the need to enhance fundamental knowledge.^1–3 In dye-sensitized solar cells (DSSCs), mesoporous thin films of anatase TiO₂ nanocrystallites are functionalized with molecular chromophores, or “sensitizers”, that extend the spectral response of these materials into the visible region. In the accepted mechanism for power generation with DSSCs, light absorption induces electron “injection” from the sensitizer's excited state to the metal oxide acceptor states.⁴ A donor present in the electrolyte solution then reduces the oxidized sensitizer, a process often termed “dye regeneration”.⁵ Competition between the collection of the injected electron and back electron transfer, or “charge recombination”, to the oxidized sensitizer or the oxidized donor often lowers the efficiency of DSSCs. This paper seeks to better understand the unwanted charge recombination reaction of the injected electrons with the oxidized donor through the use of four symmetrically substituted triphenylamines whose formal reduction potentials span a range of 0.5 eV (Scheme 1).

Scheme 1 Mechanism for the photoinitiation of the desired reaction. Visible light absorption by the ruthenium sensitizer induced rapid excited-state electron injection to the acceptor state of TiO₂, k_inj > 10⁸ s⁻¹. The oxidized sensitizer is then regenerated by triphenylamine (TPA) with a rate constant k_reg. This sequence provides the reactants for the desired charge recombination reaction of the injected electron with the oxidized triphenylamine redox mediator (k_rec) that was quantified over a 0.5 eV change in driving force.

When compared to the wealth of literature reports focused on electron transfer from TiO₂ to the oxidized sensitizer, there are a remarkably small number of systematic studies that seek to understand the factors that influence charge recombination to oxidized donors present in the electrolyte.^6–13 This is likely due to the dominance of I⁻/I₃⁻ as the prototypical redox mediator employed in DSSCs that is not easily amenable to systematic studies.^14,15 However, alternative redox mediators, such as Co(III/II) polypyridyl complexes,^16–23 triphenylamine or phenothiazine,^24,25 have provided new opportunities to gain fundamental information on how sensitive charge recombination is to the electrolyte composition,^6,26 molecular structure,^12,27 or the thermodynamic driving force.^7–9

The influence of the reaction driving force on recombination has been previously studied by several groups^7,8,10,28 and data consistent with the Marcus normal kinetic region has been reported.^29,30 Recall that in the Marcus normal region the total reorganization energy λ for electron transfer is greater than the absolute value of the Gibbs free energy change, λ > |ΔG°|. Under normal conditions, an increase in the driving force results in an increase in the rate of electron transfer. In a study of recombination to a series of substituted ferroceniums, Hupp et al. noted that normal region behavior was peculiar given the small reorganization energies and the large reaction driving forces⁸ that should have placed the reaction in the Marcus inverted region, λ > |ΔG°|. Hamann et al. have suggested that electron transfer from different electronic states in TiO₂ may mask inverted behavior similar to the case for metallic donors.³¹ Further complicating the analysis is the considerable literature that indicates that the observed rate constants abstracted from transient spectroscopic and/or electrochemical data report mainly on the diffusion of the injected TiO₂ electron and/or acceptor.^32–38 It is possible that diffusion does rate limit interfacial electron transfer in some cases, however this does not explain the reported driving force dependencies or the recent observation of specific interfacial electron transfer pathways at sensitized TiO₂ interfaces.^39,40

Nevertheless, an experimental challenge is to abstract the actual interfacial electron transfer rate constant from the transient data that are usually highly non-exponential.^32,33,41 A fitting function that has been phenomenally successful is the so-called Kohlrausch–Williams–Watts (KWW) function that was proposed empirically by Kohlrausch, and later popularized by Williams and Watts.⁴² This function was first derived by Scher and Montroll based on a random walk model and has since become a paradigm for charge transport in disordered media.⁴³ In particular the work of Nelson and coworkers has extended the KWW model to the trapping/detrapping electron transport in dye sensitized mesoporous TiO₂ thin films that are commonly used in DSSCs.^{32,37,44–46} It should be emphasized, however, that a quality fit to the KWW function does not necessarily indicate that an underlying transport mechanism is operative. For example, Anderson has derived the KWW function based on serially linked rate constants that are not necessarily associated with charge transport in disordered solids.⁴⁷

In this study, a series of four symmetrically substituted triphenylamines (TPAs) were utilized to establish a correlation between the reaction kinetics and driving force, Fig. 1. The TPA molecules were substituted at the para-position of each phenyl ring with electron donating/withdrawing functional groups that allowed the TPA^+/0 reduction potential to be varied by ∼0.5 V. A key finding was that the interfacial electron transfer became first-order when the reaction driving force was large. Such first-order behavior has not been previously reported and was maintained for the two different ruthenium sensitizers as well as the two different acetonitrile electrolytes. A Perrin-like model is proposed to rationalize this kinetic behavior. Additionally, an increase in driving force resulted in an increase in the rate of interfacial electron transfer, consistent with the reaction occurring in the Marcus normal region.

Fig. 1 Ruthenium sensitizers (RuP and RuC) and triphenylamines (TPAs) used in this study.

Results

Mesoporous nanocrystalline TiO₂ thin films were sensitized to visible light with [Ru(bpy)₂(dcb)]²⁺ (RuC) or [Ru(bpy)₂(dpb)]²⁺ (RuP) (bpy = 2,2′-bipyridine, dcb = 4,4′-dicarboxylic acid-2,2′-bipyridine and dpb = 4,4′-diphosphonic acid-2,2′-bipyridine) by immersion into concentrated sensitizer CH₃CN solutions. These films were soaked for a minimum of 24 hours to ensure that saturation surface coverages (∼10⁻⁸ mol cm⁻²) were obtained, as determined by a previously reported spectral method.⁴⁸ The sensitized films, abbreviated TiO₂|RuC and TiO₂|RuP, immersed in neat acetonitrile displayed a broad absorption band in the visible region characteristic of a metal-to-ligand charge transfer (MLCT) feature. A bathochromic shift of the absorption spectrum was observed upon the addition of 0.1 M NaClO₄ or LiClO₄ to the acetonitrile that surrounded the thin film. Such spectral shifts have previously been assigned to a change in the local electric field upon cation adsorption to the TiO₂ surface.^6,49,50 The TPAs did not appreciably absorb visible light in their neutral forms, however the one electron oxidized forms exhibited strong absorption between 600–800 nm, Fig. 2b. The peak position and the molar absorption coefficient for these absorbances are reported in Table 1.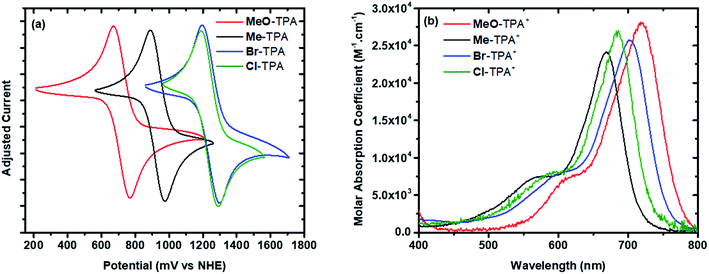

Fig. 2 Cyclic voltammograms (a) and TPA⁺ absorption spectra (b) of the indicated TPA measured in 0.1 M NaClO₄ acetonitrile electrolyte.

Table 1 Electrochemical and spectroscopic properties of the Ru sensitizers and the triphenylamines

	Oxidation potential^a (V vs. NHE)	TPA^+ peak absorbance (nm)	TPA^+ extinction coefficient (M^−1 cm^−1)
a Measured in 0.1 M NaClO4 CH3CN electrolyte unless otherwise noted. b Ref. 51, measured in 0.1 M LiClO4 CH3CN electrolyte on nanoITO. c Ref 48, measured in 0.1 M LiClO4 CH3CN electrolyte on nanocrystaline TiO2.
MeO-TPA	0.72 ± 0.01	717 ± 1	2.8 × 10^4 ± 300
Me-TPA	0.93 ± 0.01	668 ± 1	2.4 × 10^4 ± 300
Cl-TPA	1.24 ± 0.01	685 ± 1	2.7 × 10^4 ± 300
Br-TPA	1.25 ± 0.01	702 ± 1	2.6 × 10^4 ± 300
RuP	1.54^b
RuC	1.48^c

---

The TPA^+/0 reduction potentials were determined by cyclic voltammetry in 0.1 M NaClO₄ acetonitrile, Fig. 2a. The half-wave potentials were taken as an estimate for the formal reduction potentials that varied between 0.72 V (MeO-TPA) and 1.25 V vs. NHE (Br-TPA), Table 1.

Nanosecond transient absorption spectroscopy was used to quantify the recombination reaction. Experiments were performed in 0.1 M NaClO₄ acetonitrile electrolyte for TiO₂|RuC and in 0.1 M LiClO₄ acetonitrile electrolyte for TiO₂|RuP. The Lewis acidic Na⁺ or Li⁺ cations were present in the external electrolyte to improve the excited state injection yield.^49,52,53 It is worth noting that no specific interaction between the cations and the TPA is expected based on previous literature⁶ but these cations have been shown to influence the rate for recombination from TiO₂(e⁻) to Me-TPA⁺, with rate constants following the trend Na⁺ ≥ Li⁺ > Mg²⁺ > Ca²⁺.⁶ Such a trend was also observed for the recombination to I₃⁻.²⁶ In a typical experiment, pulsed 532 nm light excitation of the sensitized TiO₂ thin films submerged in argon purged 0.1 M NaClO₄ or 0.1 M LiClO₄ acetonitrile electrolytes with 8 mM of a selected TPA derivative formed the initial charge separated state, TiO₂(e⁻)|RuC⁺ or TiO₂(e⁻)|RuP⁺. The subsequent absorption changes were monitored on a 10 ns or longer time scale. Absorption changes associated with the oxidized sensitizer were observed within the instrument response time consistent with rapid excited state injection (k_inj > 10⁸ s⁻¹).^2,4 Under all conditions studied, the transient spectra were simulated with a linear combination of standard spectra comprised of: (1) TiO₂|RuC and the oxidized form of the sensitizer, abbreviated TiO₂|RuC⁺; (2) TPA⁺; and/or (3) the Stark effect.^49,54,55 The Stark effect results from local electric fields generated by cation adsorption and/or the injected electron which are themselves well simulated by a first derivative of the ground state sensitizer absorption. In principle, the injected electron also contributes to the transient spectra, however its weak absorption was obscured by the more intense absorption associated with TPA⁺.

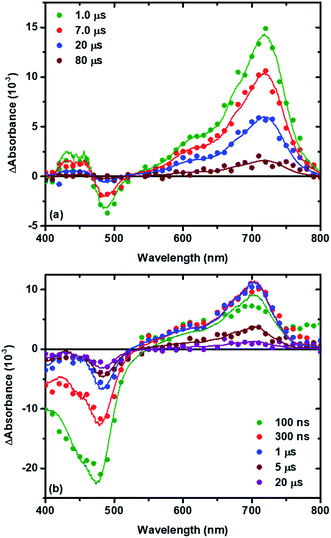
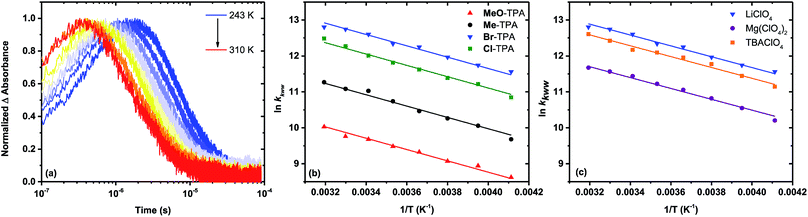
Fig. 3 shows representative absorption difference spectra measured after pulsed light excitation of TiO₂|RuC immersed in 0.1 M NaClO₄ acetonitrile solution with 8 mM MeO-TPA (Fig. 3a) or 8 mM Cl-TPA (Fig. 3b). Contributions to the spectra from the oxidized sensitizer were absent after 1 μs with MeO-TPA (or Me-TPA) and the relative amplitudes were consistent with quantitative regeneration of the oxidized sensitizer. This was true for either sensitizer in both electrolytes and enabled the desired reaction, TiO₂(e⁻) + TPA⁺ → TiO₂ + TPA, to be quantified on a microsecond or longer timescale without contributions from slow regeneration and the oxidized sensitizer. In contrast, regeneration by Cl-TPA (or Br-TPA) was not quantitative on any time scale and contributions from the oxidized sensitizer were evident on all delay times.

Fig. 3 Transient absorption spectra measured at indicated delay times after pulsed 532 nm excitation of TiO₂|RuC submerged in 0.1 M NaClO₄ acetonitrile electrolyte with 8 mM MeO-TPA (a) or 8 mM Cl-TPA (b). Overlaid as solid lines are the simulated spectra.

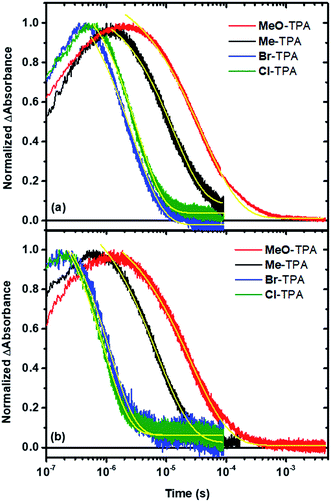
The time dependent concentration of TPA⁺ was biphasic, consisting of an initial rise followed by a decay, Fig. 4. For transient absorption data acquired with MeO-and Me-TPA, a sum of two Kohlrausch–William–Watts (KWW) functions adequately modelled the kinetic data, n = 2, as shown in eqn (1). The regeneration of the oxidized sensitizer was quantified independently from single wavelength absorption data monitored at 402 nm, which represented an isosbestic point for the Stark effect, that was fit to a single KWW function; the obtained values for β and k were used to constrain fits to the bi-KWW function used to model the TPA⁺ kinetics as β₁ and k₁. An “average” rate constant, k_kww, was then calculated as the first moment of this distribution using eqn (2), where Γ is the Gamma function.

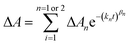Fig. 4 Single wavelength absorption changes measured after pulsed 532 nm laser excitation of TiO₂|RuP in 0.1 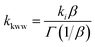M LiClO₄ acetonitrile electrolyte (a) and TiO₂|RuC in 0.1 M NaClO₄ acetonitrile electrolyte (b) with 8 mM of the indicated TPA mediator. Kinetics were monitored at the TPA⁺ absorption peak. Fits to the KWW model are overlaid on the data as solid yellow lines.

Fits of the recombination data for electron transfer from TiO₂(e⁻) to Cl- or Br-TPA⁺ using a single KWW function revealed a β value of 1, while the corresponding data obtained for MeO-TPA and Me-TPA required β values ranging between 0.62 and 0.85. A β value of unity corresponds to the single exponential behavior expected for a first-order kinetic reaction. The kinetics were independent of the excitation irradiance and hence the initial concentrations, resulting in normalizable kinetics that allowed a single rate constant to model the desired reaction. A summary of the fitting parameters is given in Table 2. Note that the rate constants for recombination from TiO₂(e⁻) to all TPA⁺ derivatives were larger in Na⁺ than in Li⁺ consistent with previous report.⁶

Table 2 Charge recombination rate constants abstracted from the KWW model^a

	k (10^5 s^−1), ^bβ TiO2|RuC	k kww (10^5 s^−1) ^bTiO2|RuC	k (10^5 s^−1), ^cβ TiO2|RuP	k kww (10^5 s^−1) ^cTiO2|RuP
a Rate constants (krec) for electron transfer from TiO2(e^−) to TPA^+, where k represents the rate constant extracted from fits to eqn (1) and kkww represents the average rate constant calculated with eqn (2). Note that for Cl-TPA and Br-TPA, the recombination was first-order such that β = 1 and kcr and kkww are equivalent. b Measured in 0.1 M NaClO4 CH3CN electrolyte. c Measured in 0.1 M LiClO4 CH3CN electrolyte.
MeO-TPA	0.42 ± 0.05, 0.67	0.47 ± 0.04	0.27 ± 0.03, 0.62	0.19 ± 0.02
Me-TPA	1.5 ± 0.1, 0.74	1.7 ± 0.1	0.74 ± 0.07, 0.85	0.68 ± 0.02
Cl-TPA	12.0 ± 0.3, 1	12 ± 0.1	3.1 ± 0.1, 1	3.1 ± 0.1
Br-TPA	9.7 ± 0.1, 1	9.7 ± 0.1	3.3 ± 0.1, 1	3.3 ± 0.1

---

Kinetic data acquired as a function of temperature were modeled using the procedure described for the room temperature data, Fig. 5a. The Arrhenius plot of the first-order rate constant (Cl-TPA or Br-TPA) or the average rate constants (k_kww) is shown in Fig. 5b, and revealed a common activation energy E_a = 0.13 ± 0.01 eV for all TPA⁺ acceptors. The E_a values obtained for the recombination to Br-TPA⁺ in 0.1 M MgClO₄ and 0.1 M TBAClO₄ CH₃CN electrolytes were the same within experimental error (Fig. 5c). The recombination to Br-TPA⁺ in 0.1 M MgClO₄ was slower than that in LiClO₄ or NaClO₄. Interestingly, even though the identity of the cation changed the rate of charge recombination, the activation energy remained the same.

Fig. 5 Single wavelength absorption changes measured after pulsed 532 nm laser excitation of TiO₂|RuP in 0.1 M LiClO₄ with 8 mM of Br-TPA at indicated temperatures (a). Kinetics were monitored at the TPA⁺ absorption peak. Arrhenius plots for the recombination from TiO₂|RuP to the indicated TPAs in 0.1 M LiClO₄ (b) and from TiO₂|RuP to Br-TPA in the indicated 0.1 M CH₃CN electrolytes (c).

Discussion

The intent of this study was to quantify the driving force dependence of the interfacial charge recombination reaction photogenerated electrons in dye-sensitized TiO₂, TiO₂(e⁻)s, with oxidized triphenylamines to yield ground state products, eqn (3).

TiO₂(e⁻) + TPA⁺ → TiO₂ + TPA (3)

If one assumes that the reducing power of the TiO₂(e⁻) is insensitive to the TPA derivative used, the Gibbs free energy change was varied by over 500 meV. The reactants were produced by pulsed laser excitation of the sensitizers (RuC or RuP) that initiated rapid excited state injection, k_inj > 10⁸ s⁻¹, into TiO₂ followed by diffusional ‘regeneration’ through TPA oxidation in an acetonitrile electrolyte. The time required for regeneration of the oxidized sensitizer by TPA was about 1 microsecond and occurred quantitatively for the more easily oxidized TPA derivatives.

The data provide new insights into the origin(s) of the non-exponential kinetics that are often reported for interfacial charge recombination reactions in dye-sensitized TiO₂ materials. Specifically, the observation of a first-order reaction indicates a strong coulombic attraction between TiO₂(e⁻) and TPA⁺ that provides a pathway for charge recombination. Consistent with previous reports, the kinetic data indicates that eqn (3) occurs in the Marcus normal kinetic region, despite the large expected driving forces. Below we discuss in more detail a kinetic reaction sphere model for charge recombination followed by a description of the driving force dependence.

Kinetic model

The spectroscopic approach described provided equal numbers of injected electrons and oxidized TPA compounds. A rate law that is first-order in TPA⁺ and first-order in TiO₂(e⁻) and hence second-order overall might be expected, eqn (4).

Rate = k[TPA⁺][TiO₂(e⁻)] ∼ k[TPA⁺]n^β (4)

The order in TiO₂(e⁻) has been quantified by many groups, through transient photovoltage spectroscopy, and is mysteriously often reported to be non-integral^56,57 although under some conditions it is indeed unity.⁵⁸ Since the molar concentrations asserted by the brackets in eqn (4) are ill-defined in the mesoporous TiO₂ thin films, the total number of injected electrons, n, is often raised to the exponent β as an approximation to the [TiO₂(e⁻)].²

A striking result from this study was that when charge recombination was highly exothermic, the kinetic data were most accurately modelled as a first-order kinetic model and displayed single exponential kinetics even when the initial concentration was varied by over a factor of five. Such data is inconsistent with the rate law implied by eqn (4). Instead, first-order recombination is expected for a unimolecular electron transfer like that observed in covalently linked Donor–Acceptor (D–A) compounds. Therefore, electron transfer is to the surface adsorbed TPA⁺ proximate to the injected electron, eqn (5).

TiO₂(e⁻)|TPA⁺ → TiO₂|TPA (5)

Hence, diffusional regeneration of the oxidized dye yields TPA⁺ that adsorbs to the TiO₂ surface prior to charge recombination. It is likely that the coulombic attraction between the injected electron and TPA⁺ stabilizes the proposed adduct. Indeed, the electric field produced by excited state injection has been estimated to be ∼2 MV cm⁻¹ under one-sun illumination.^49,50 The field is sufficiently large to electrostatically bind the cationic TPA⁺ and the injected electron is suitably close to afford the electronic coupling necessary for electron transfer.

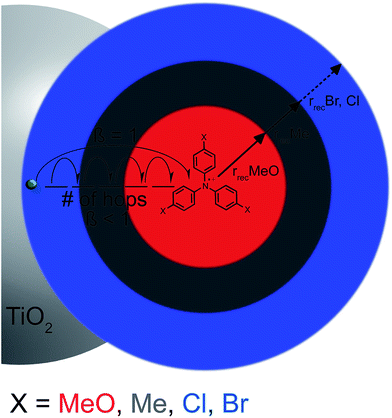
In order to rationalize why the reaction becomes non-exponential at smaller driving forces, a “reaction sphere” model is proposed that shares some similarities with those of Perrin and Onsager (Scheme 2).^59,60 In this model, it is assumed that the injected electrons reside in localized trap states as Ti(III) species that can either hop to a Ti(IV) site or reduce surface adsorbed TPA⁺. Such Ti(IV/III) hopping is conceptually equivalent to previously reported trapping/detrapping mechanisms^46,61 and is expected to be independent of the TPA⁺ derivative. A key aspect of this model is that the TiO₂(e⁻) reacts with any TPA⁺ within a sphere whose radius r increases with driving force. Recombination within the reaction sphere gives rise to first-order kinetics; recombination to TPA⁺ outside the sphere requires Ti(IV/III) hopping, manifested as dispersive kinetics and β < 1 in the KWW function, until the rate constant for electron transfer to TPA⁺ is sufficiently large to compete with transfer to another Ti(IV) site.

Scheme 2 A reaction sphere model for interfacial charge recombination. Schematic representation of a proposed Perrin-like model. When the driving force for recombination is large, as seen for Br- and Cl-TPA, electron transfer occurs over relatively large distances (blue sphere). With smaller driving force, the electron must hop closer to the TPA⁺ acceptor before electron transfer can occur (red sphere), leading to a decreased β value in fits to the KWW function.

As first derived by Scher and Montroll,⁴³ electron transport in disordered media naturally gives rise to dispersive kinetics that follow the Kohlrausch–Williams–Watts model, eqn (6).

A(t) = A₀ exp(−kt)^β (6)

where β is inversely related to the width of the underlying Lévy distribution of rate constants, 0 < β < 1, A₀ is the initial absorbance, and k is the characteristic rate constant. When β = 1, a first-order reaction is recovered. The inverse Laplace transform of eqn (6) is known analytically for certain β values and has been determined by saddle-point approximation for others. Fig. 6 shows the distributions for charge recombination to the TPA⁺ derivatives under study as well as their average rate constants (eqn (2)) and the first-order rate constants for Cl- and Br-TPA⁺. While inverse Laplace transforms are ill-conditioned and should be viewed with caution, the highly dispersive kinetics that span at least three orders of magnitude in time likely reflect the heterogeneous Ti(IV/III) hopping transport in the mesoporous thin films. When the injected electron is within the reaction sphere, electron transfer to TPA⁺ kinetically outcompetes hopping to another Ti(IV) site. When the injected electron is outside the reaction sphere, a wide range of rate constants is possible due to the weak coupling and hence small electron transfer rate constants to TPA⁺. We emphasize that this model, like those of Perrin’s and Onsager’s, is an approximation. Electron transfer to TPA⁺ likely occurs at a distribution of distances that are not marked by a sharp turn on/off at radius r.

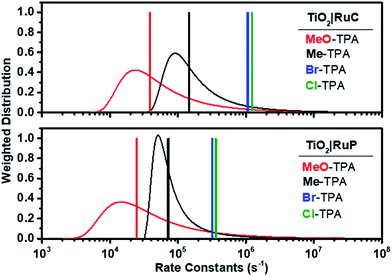Fig. 6 Calculated Lévy distribution of the charge recombination rate constants abstracted from transient data for electron transfer from TiO₂(e⁻)|RuC (top) and TiO₂(e⁻)|RuP (bottom) to MeO-TPA⁺ (red) or to Me-TPA⁺ (black). An average rate constant based on eqn (2) is shown as a vertical line. Also shown as vertical lines are the first-order rate constants for recombination to Br-TPA⁺ (blue) and Cl-TPA⁺ (green).

It is interesting to note that the E_a value of 0.13 ± 0.01 eV was independent of the identity of the TPA⁺ acceptor. A similar activation energy of 0.13 eV was reported for electron transport within mesoporous TiO₂ (ref. 45) as well as for Li⁺ hops in a Li₁₀SnP₂S₁₂-based composite.⁶² Cation hopping was excluded since the same activation energy was measured in 0.1 M MgClO₄ and 0.1 M TBAClO₄ electrolytes for recombination to Br-TPA⁺ (Fig. 5c). Since the observed rate constant is the true rate constant for recombination to Cl- and Br-TPA⁺, the activation energy must reflect the barrier for the interfacial electron transfer reaction. For the other TPA⁺ derivatives, the same E_a value should be taken as the average of a distribution of activation energies as it was extracted from rate constants based on Lévy distributions. The fact that these average activation energies are the same within experimental error indicates that the barrier for Ti(IV/III) hopping must be very similar to that for electron transfer to the oxidized TPA⁺, a conclusion that is in agreement with a recent publication.⁴⁵

Marcus normal electron transfer

Regardless of how the time resolved data is analyzed, the data clearly show that the recombination rate becomes larger as the E^o(TPA^+/0) potential increases, consistent with Marcus normal kinetic behavior. There was no evidence for activationless or Marcus inverted kinetic behaviors even when the mediator potentials were tuned to the most positive values. Indeed, the electron transfer was clearly activated, E_a = 0.13 ± 0.01 eV. Normal kinetic behavior has also been reported for Co(III) complexes and for ferrocenium acceptors.^7,8,28 While a precise value of the formal E^oTi(IV/III) reduction potential is unknown, the onset for spectroscopic changes attributed to TiO₂(e⁻) is around 0 V vs. NHE in 0.1 M LiClO₄.^6,49 Hence, the spectroelectrochemical studies suggest that the driving force for recombination to X-TPA⁺ acceptors, where X = Cl or Br, is greater than 1.2 eV. We emphasize however that the true free energy change for charge recombination is unknown and may be complicated by the time dependent electric field^26,63 or the exponential density of donor states that are often invoked to model such data.^49,64 Nevertheless, the data is fully consistent with Marcus normal electron transfer and suggests that either the reorganization energy must exceed this value or, as has been previously described, that recombination occurs through lower energy “trap” states with a significantly smaller driving force.^10,31

The total reorganization energy for this interfacial recombination reaction includes contributions from TiO₂, the triphenylamine acceptors, and the electrolyte solution. Theoretical calculations indicate that λ_tot = 0.15–0.25 eV for TPA^+/0 which is consistent with the rapid self-exchange in this class of compound.⁶⁵ The reorganization energy change associated with Ti(IV/III) hopping is unknown. In molecular compounds, the d⁰/d¹ redox chemistry is subject to a large Jahn–Teller distortion and reported reorganization energies are quite large.^66–68 While molecular Ti compounds and TiO₂ are quite different, the spectroscopic properties of Ti(III) in the solid state often show clear evidence of Jahn–Teller distortions.^69,70 Hence, a significant inner sphere contribution to the reorganization energy is expected.^66–68 The dielectric continuum theory provides outer-sphere reorganization of ∼1 eV in acetonitrile.^71,72 Recently, reorganization energies near 1.2 eV for electron hopping have been calculated using the DFT + U method.⁷³ Hence it is not unreasonable to suggest that the total reorganization energy is greater than 1.2 eV. Alternatively, and as has previously been discussed,^28,31 a lower driving force for the reaction would be expected if the energetic position of the TiO₂ donor states that participate in charge recombination is at much more positive potentials than the spectroelectrochemical data indicates. This would allow for the observation of normal behavior when the total reorganization energy is less than 1.2 eV.

In the present study, the first-order recombination observed for the halogenated TPAs rules out diffusion or transport of the injected electrons as being a rate limiting process. Furthermore, recent studies have shown that charge recombination to oxidized dyes is sensitive to the bridge that separates them from the surface or the orientation of the surface linker.^39,40 Indeed, specific bridge mediated pathways to oxidized dyes have been identified.³⁷ Taken together, these findings indicate that the observed rate constants do, at least partially, report upon the interfacial electron transfer rate constant(s). Even when |ΔG°| was as large as that reported here there was no evidence for first-order kinetics or rate constants that were highly sensitive to the sensitizer E^o(S^+/0) reduction potentials. This very different behavior for electron transfer to oxidized sensitizers versus redox mediators is not fully understood. A working hypothesis is that the anionic phosphonate (or carboxylate) binding groups preclude close-encounters of the injected electrons with the oxidized sensitizers resulting in more dispersive kinetics with longer distance interfacial electron transfer.

Conclusion

Electron transfer from TiO₂ to a series of symmetrically substituted oxidized triphenylamines was quantified over a driving force range of 0.5 eV. The rates increased with the thermodynamic driving force, consistent with the reaction occurring in the Marcus normal region. This conclusion was robust and occurred for two different CH₃CN electrolytes (LiClO₄ and NaClO₄) and when sensitized to visible light by two different sensitizers (RuC and RuP). An unprecedented first-order electron transfer from TiO₂ to Cl-or Br-TPA⁺ indicated a coulombic interaction that provided sufficient coupling for unimolecular-like recombination. A reaction sphere model was proposed to account for this behavior and the dispersive kinetics observed for the other TPA⁺ acceptors wherein the recombination radius is related to the Gibbs free energy change.

Experimental

Materials

The following reagents and solvents were purchased from the listed commercial sources and used without further purification: acetonitrile (Burdick and Jackson, spectrophotometric grade), methanol (Fischer, ACS Reagent grade), sodium perchlorate (NaClO₄, Sigma-Aldrich, 99%), argon gas (Airgas, >99.998%), [Ru(bpy)₂(dcb)]²⁺(PF₆)₂ (Solaronix), tri-p-tolyl-amine (Me-TPA, Sigma-Aldrich, 97%), and tris(4-bromophenyl)amine (Br-TPA, Sigma-Aldrich, 98%). [Ru(bpy)₂(dpb)]²⁺(PF₆)₂,⁷⁷ tri-p-anisylamine (MeO-TPA)⁷⁴ and tris (4-chlorophenyl)amine (Cl-TPA)⁷⁵ were prepared according to previously reported methods.

Materials preparation

Anatase TiO₂ nanocrystallites were prepared through a previously described sol–gel method.⁷⁶ The sols were cast as thin films by doctor blading onto methanol cleaned glass substrates. Scotch tape (∼10 μm) was used as a spacer and aided in achieving a uniform film thickness. The films were allowed to stand covered for 30 min before being transferred to a tube furnace. The furnace was first purged with pure O₂, then heated at 450 °C for 30 min. After annealing, the films were either kept in a 70 °C oven for later use, or immediately submerged in concentrated acetonitrile solution of RuC or RuP.

Electrochemistry

All electrochemical experiments were performed in acetonitrile solution containing 0.1 M NaClO₄ as the supporting electrolyte. Potentials were applied against a self-contained Ag wire pseudo reference electrode containing the same electrolyte solution. The reference electrode was calibrated externally against the Fc^+/0 reduction potential (0.31 V vs. SCE) where SCE is 0.241 V positive of NHE.⁷⁸ Cyclic voltammetry employed Pt disk electrodes (BASi, 1.6 mm diameter) as both working and auxiliary electrodes. Spectroelectrochemical studies were performed using a gold Honeycomb Spectroelectrochemical Cell (Pine Research Instrumentation), and allowed absorption changes to be quantified after application of an electrochemical bias.

Absorption spectra

Ground state absorption spectra were obtained from a Varian Cary 50 spectrophotometer. Serial dilution of stock solution was used to determine the extinction coefficient of each compound. Molar absorption coefficient for the one electron oxidized TPAs were determined by internal comparison to the ground state TPA spectra.

Transient absorption

Nanosecond transient absorption measurements were performed on a previously described apparatus.⁷⁹ A pulsed (1 Hz) 150 W xenon arc lamp (Applied Photophysics) was used as the probe beam. Appropriate filters were placed before the sample to prevent direct band gap excitation of TiO₂. After passing through the sample, the probe beam was focused into a Spex monochromator coupled to a R928 Hamamatsu photomultiplier tube. A pulsed (1 Hz) Nd:YAG laser (Quantel USA Brilliant B; 5–6 ns full width at half-maximum, spot size ∼0.8 cm²) provided sample excitation. Excitation power was measured at the sample using a thermopile power meter (Molectron), with typical excitation powers varying between 500 μJ and 5 mJ per pulse. Typically, 30 pump-probe measurements were averaged over the range of 400–800 nm. Data generated for kinetic modeling were typically averaged between 150–210 measurements in order to improve signal to noise. Full spectra were generated at a set time after laser excitation by averaging 3–21 data points around the timepoint of interest.

Data modeling

Kinetic modeling was performed with OriginPro 9, which utilizes a Levenberg–Marquardt iteration method. A custom Mathematica 9 script was used to model the spectral signatures observed in transient absorption. Fitting was achieved through standard addition of steady state absorption spectra.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge support by a grant from the Division of Chemical Sciences, Office of Basic Energy Sciences, Office of Energy Research, U.S. Department of Energy (Grant DE-SC0013461). L. T.-G. would like to acknowledge the Belgian American Educational Foundation (BAEF) as well as the Bourse d’Excellence Wallonie-Bruxelles (WBI World) for generous support.

References

1. N. S. Lewis, J. Phys. Chem. B, 1998, 102, 4843–4855.
2. S. Ardo and G. J. Meyer, Chem. Soc. Rev., 2009, 38, 115–164.
3. T. Hisatomi, J. Kubota and K. Domen, Chem. Soc. Rev., 2014, 43, 7520–7535.
4. D. F. Zigler, Z. A. Morseth, L. Wang, D. L. Ashford, M. K. Brennaman, E. M. Grumstrup, E. C. Brigham, M. K. Gish, R. J. Dillon, L. Alibabaei, G. J. Meyer, T. J. Meyer and J. M. Papanikolas, J. Am. Chem. Soc., 2016, 138, 4426–4438.
5. A. Listorti, B. O’Regan and J. R. Durrant, Chem. Mater., 2011, 23, 3381–3399.
6. B. N. DiMarco, R. M. O’Donnell and G. J. Meyer, J. Phys. Chem. C, 2015, 119, 21599–21604.
7. T. W. Hamann, O. K. Farha and J. T. Hupp, J. Phys. Chem. C, 2008, 112, 19756–19764.
8. M. J. DeVries, M. J. Pellin and J. T. Hupp, Langmuir, 2010, 26, 9082–9087.
9. S. M. Feldt, G. Wang, G. Boschloo and A. Hagfeldt, J. Phys. Chem. C, 2011, 115, 21500–21507.
10. S. M. Feldt, P. W. Lohse, F. Kessler, M. K. Nazeeruddin, M. Grätzel, G. Boschloo and A. Hagfeldt, Phys. Chem. Chem. Phys., 2013, 15, 7087.
11. B. M. Klahr and T. W. Hamann, J. Phys. Chem. C, 2009, 113, 14040–14045.
12. Y. Xie, J. Baillargeon and T. W. Hamann, J. Phys. Chem. C, 2015, 119, 28155–28166.
13. Y. Xie and T. W. Hamann, J. Phys. Chem. Lett., 2013, 4, 328–332.
14. J. G. Rowley, S. Ardo, Y. Sun, F. N. Castellano and G. J. Meyer, J. Phys. Chem. C, 2011, 115, 20316–20325.
15. J. G. Rowley, B. H. Farnum, S. Ardo and G. J. Meyer, J. Phys. Chem. Lett., 2010, 1, 3132–3140.
16. J.-H. Yum, E. Baranoff, F. Kessler, T. Moehl, S. Ahmad, T. Bessho, A. Marchioro, E. Ghadiri, J.-E. Moser, C. Yi, M. K. Nazeeruddin and M. Grätzel, Nat. Commun., 2012, 3, 631.
17. T. W. Hamann, Dalton Trans., 2012, 41, 3111.
18. E. Mosconi, J.-H. Yum, F. Kessler, C. J. Gómez García, C. Zuccaccia, A. Cinti, M. K. Nazeeruddin, M. Grätzel and F. De Angelis, J. Am. Chem. Soc., 2012, 134, 19438–19453.
19. S. M. Feldt, E. a. Gibson, E. Gabrielsson, L. Sun, G. Boschloo and A. Hagfeldt, J. Am. Chem. Soc., 2010, 132, 16714–16724.
20. T. Daeneke, A. J. Mozer, T.-H. Kwon, N. W. Duffy, A. B. Holmes, U. Bach and L. Spiccia, Energy Environ. Sci., 2012, 5, 7090.
21. T. Daeneke, T.-H. Kwon, A. B. Holmes, N. W. Duffy, U. Bach and L. Spiccia, Nat. Chem., 2011, 3, 211–215.
22. Y. Saygili, M. Söderberg, N. Pellet, F. Giordano, Y. Cao, A. B. Muñoz-García, S. M. Zakeeruddin, N. Vlachopoulos, M. Pavone, G. Boschloo, L. Kavan, J.-E. Moser, M. Grätzel, A. Hagfeldt and M. Freitag, J. Am. Chem. Soc., 2016, 138, 15087–15096.
23. M. Freitag, F. Giordano, W. Yang, M. Pazoki, Y. Hao, B. Zietz, M. Grätzel, A. Hagfeldt and G. Boschloo, J. Phys. Chem. C, 2016, 120, 9595–9603.
24. Y. Hao, W. Yang, L. Zhang, R. Jiang, E. Mijangos, Y. Saygili, L. Hammarström, A. Hagfeldt and G. Boschloo, Nat. Commun., 2016, 7, 13934.
25. S. Cazzanti, S. Caramori, R. Argazzi, C. M. Elliott and C. A. Bignozzi, J. Am. Chem. Soc., 2006, 128, 9996–9997.
26. R. N. Sampaio, R. M. O’Donnell, T. J. Barr and G. J. Meyer, J. Phys. Chem. Lett., 2014, 5, 3265–3268.
27. S. A. Sapp, C. M. Elliott, C. Contado, S. Caramori and C. A. Bignozzi, J. Am. Chem. Soc., 2002, 124, 11215–11222.
28. S. M. Feldt, P. W. Lohse, F. Kessler, M. K. Nazeeruddin, M. Gratzel, G. Boschloo and A. Hagfeldt, Phys. Chem. Chem. Phys., 2013, 15, 7087–7097.
29. N. Sutin, Acc. Chem. Res., 1982, 15, 275–282.
30. P. F. Barbara, T. J. Meyer and M. a. Ratner, J. Phys. Chem., 1996, 100, 13148–13168.
31. J. W. Ondersma and T. W. Hamann, J. Am. Chem. Soc., 2011, 133, 8264–8271.
32. M. Ansari-Rad, J. A. Anta and J. Bisquert, J. Phys. Chem. C, 2013, 117, 16275–16289.
33. M. Ansari-Rad, Y. Abdi and E. Arzi, J. Phys. Chem. C, 2012, 116, 3212–3218.
34. J. Bisquert, A. Zaban and P. Salvador, J. Phys. Chem. B, 2002, 106, 8774–8782.
35. S. A. Haque, Y. Tachibana, D. R. Klug and J. R. Durrant, J. Phys. Chem. B, 1998, 102, 1745–1749.
36. A. V. Barzykin and M. Tachiya, J. Phys. Chem. B, 2002, 106, 4356–4363.
37. R. Katoh, A. Furube, A. V. Barzykin, H. Arakawa and M. Tachiya, Coord. Chem. Rev., 2004, 248, 1195–1213.
38. R. Katoh and A. Furube, J. Phys. Chem. Lett., 2011, 2, 1888–1891.
39. K. Hu, A. D. Blair, E. J. Piechota, P. A. Schauer, R. N. Sampaio, F. G. L. Parlane, G. J. Meyer and C. P. Berlinguette, Nat. Chem., 2016, 8, 853–859.
40. K. E. Spettel and N. H. Damrauer, J. Phys. Chem. C, 2016, 120, 10815–10829.
41. A. N. M. Green, E. Palomares, S. A. Haque, J. M. Kroon and J. R. Durrant, J. Phys. Chem. B, 2005, 109, 12525–12533.
42. G. Williams and D. C. Watts, Trans. Faraday Soc., 1970, 66, 80.
43. H. Scher and E. W. Montroll, Phys. Rev. B, 1975, 12, 2455–2477.
44. J. Bisquert, F. Fabregat-Santiago, I. Mora-Seró, G. Garcia-Belmonte and S. Giménez, J. Phys. Chem. C, 2009, 113, 17278–17290.
45. G. Boschloo and A. Hagfeldt, J. Phys. Chem. B, 2005, 109, 12093–12098.
46. J. Nelson, S. A. Haque, D. R. Klug and J. R. Durrant, Phys. Rev. B, 2001, 63, 205321.
47. R. G. Palmer, D. L. Stein, E. Abrahams and P. W. Anderson, Phys. Rev. Lett., 1984, 53, 958–961.
48. B. N. DiMarco, T. C. Motley, R. S. Balok, G. Li, M. A. Siegler, R. M. O’Donnell, K. Hu and G. J. Meyer, J. Phys. Chem. C, 2016, 120, 14226–14235.
49. R. M. O’Donnell, R. N. Sampaio, T. J. Barr and G. J. Meyer, J. Phys. Chem. C, 2014, 118, 16976–16986.
50. C. L. Ward, R. M. O’Donnell, B. N. DiMarco and G. J. Meyer, J. Phys. Chem. C, 2015, 119, 25273–25281.
51. B. H. Farnum, Z. A. Morseth, M. K. Brennaman, J. M. Papanikolas and T. J. Meyer, J. Am. Chem. Soc., 2014, 136, 15869–15872.
52. C. A. Kelly, F. Farzad, D. W. Thompson, J. M. Stipkala and G. J. Meyer, Langmuir, 1999, 15, 7047–7054.
53. D. F. Watson and G. J. Meyer, Coord. Chem. Rev., 2004, 248, 1391–1406.
54. S. Ardo, Y. Sun, A. Staniszewski, F. N. Castellano and G. J. Meyer, J. Am. Chem. Soc., 2010, 132, 6696–6709.
55. U. B. Cappel, S. M. Feldt, J. Schöneboom, A. Hagfeldt and G. Boschloo, J. Am. Chem. Soc., 2010, 132, 9096–9101.
56. E. C. Brigham and G. J. Meyer, J. Phys. Chem. C, 2014, 118, 7886–7893.
57. P. R. F. Barnes, K. Miettunen, X. Li, A. Y. Anderson, T. Bessho, M. Gratzel and B. C. O’Regan, Adv. Mater., 2013, 25, 1881–1922.
58. T. J. Barr and G. J. Meyer, ACS Energy Lett., 2017, 2, 2335–2340.
59. F. Perrin, Ann. Phys., 1929, 10, 169–275.
60. L. Onsager, J. Am. Chem. Soc., 1936, 58, 1486–1493.
61. J. Nelson, Phys. Rev. B, 1999, 59, 15374–15380.
62. M. Kaus, H. Stöffler, M. Yavuz, T. Zinkevich, M. Knapp, H. Ehrenberg and S. Indris, J. Phys. Chem. C, 2017, 121, 23370–23376.
63. R. M. O’Donnell, S. Ardo and G. J. Meyer, J. Phys. Chem. Lett., 2013, 4, 2817–2821.
64. B. C. O’Regan and J. R. Durrant, Acc. Chem. Res., 2009, 42, 1799–1808.
65. P. Cias, C. Slugovc and G. Gescheidt, J. Phys. Chem. A, 2011, 115, 14519–14525.
66. E. A. Robinson and J. E. Earley, Inorg. Chem., 1999, 38, 4128–4131.
67. O. Olubuyide, K. Lu, A. O. Oyetunji and J. E. Earley, Inorg. Chem., 1986, 25, 4798–4799.
68. C. Creutz and M. H. Chou, Inorg. Chem., 2008, 47, 3509–3514.
69. W. R. Entley, C. R. Treadway, S. R. Wilson and G. S. Girolami, J. Am. Chem. Soc., 1997, 119, 6251–6258.
70. R. Ameis, D. Reinen and S. Kremer, Inorg. Chem., 1985, 24, 2751–2754.
71. E. H. Yonemoto, G. B. Saupe, R. H. Schmehl, S. M. Hubig, R. L. Riley, B. L. Iverson and T. E. Mallouk, J. Am. Chem. Soc., 1994, 116, 4786–4795.
72. Y.-P. Liu and M. D. Newton, J. Phys. Chem., 1994, 98, 7162–7169.
73. N. A. Deskins and M. Dupuis, Phys. Rev. B, 2007, 75, 195212.
74. C. Quinton, V. Alain-Rizzo, C. Dumas-Verdes, F. Miomandre, G. Clavier and P. Audebert, RSC Adv., 2014, 4, 34332.
75. A. P. Davis and A. J. Fry, J. Electrochem. Soc., 2013, 160, G3091–G3096.
76. T. A. Heimer, S. T. D’Arcangelis, F. Farzad, J. M. Stipkala and G. J. Meyer, Inorg. Chem., 1996, 35, 5319–5324.
77. M. R. Norris, J. J. Concepcion, C. R. K. Glasson, Z. Fang, A. M. Lapides, D. L. Ashford, J. L. Templeton and T. J. Meyer, Inorg. Chem., 2013, 52, 12492–12501.
78. A. J. Bard and L. R. Faulkner, Electrochemical Methods: Fundementals and Applications, Wiley, New York, 2nd edn, 2001.
79. R. Argazzi, C. A. Bignozzi, T. A. Heimer, F. N. Castellano and G. J. Meyer, Inorg. Chem., 1994, 33, 5741–5749.

---