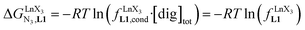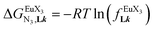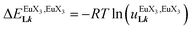Open Access Article
Open Access ArticleCooperative loading of multisite receptors with lanthanide containers: an approach for organized luminescent metallopolymers†
Lucille
Babel
a,
Laure
Guénée
b,
Céline
Besnard
b,
Svetlana V.
Eliseeva
 c,
Stéphane
Petoud
*c and
Claude
Piguet
c,
Stéphane
Petoud
*c and
Claude
Piguet
 *a
*a
aDepartment of Inorganic and Analytical Chemistry, University of Geneva, 30 quai E. Ansermet, CH-1211 Geneva 4, Switzerland. E-mail: Claude.Piguet@unige.ch
bLaboratory of Crystallography, University of Geneva, 24 quai E. Ansermet, CH-1211 Geneva 4, Switzerland
cCentre de Biophysique Moléculaire, CNRS UPR 4301, Rue Charles Sadron, F-45071 Orléans Cedex 2, France. E-mail: Stephane.Petoud@cnrs-orleans.fr
First published on 6th November 2017
Abstract
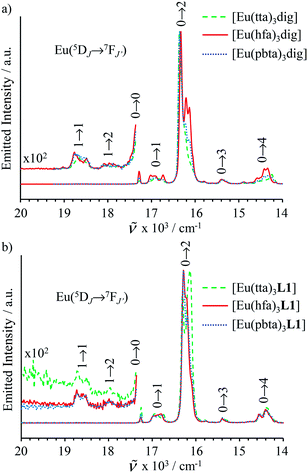
Metal-containing (bio)organic polymers are materials of continuously increasing importance for applications in energy storage and conversion, drug delivery, shape-memory items, supported catalysts, organic conductors and smart photonic devices. The embodiment of luminescent components provides a revolution in lighting and signaling with the ever-increasing development of polymeric light-emitting devices. Despite the unique properties expected from the introduction of optically and magnetically active lanthanides into organic polymers, the deficient control of the metal loading currently limits their design to empirical and poorly reproducible materials. We show here that the synthetic efforts required for producing soluble multi-site host systems Lk are largely overcome by the virtue of reversible thermodynamics for mastering the metal loading with the help of only two parameters: (1) the affinity of the luminescent lanthanide container for a single binding site and (2) the cooperative effect which modulates the successive fixation of metallic units to adjacent sites. When unsymmetrical perfluorobenzene-trifluoroacetylacetonate co-ligands (pbta−) are selected for balancing the charge of the trivalent lanthanide cations, Ln3+, in six-coordinate [Ln(pbta)3] containers, the explored anti-cooperative complexation processes induce nearest-neighbor intermetallic interactions 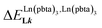 twice as large as thermal energy at room temperature (RT = 2.5 kJ mol−1). These values have no precedent when using standard symmetrical containers and they pave the way for programming metal alternation in luminescent lanthanidopolymers.
twice as large as thermal energy at room temperature (RT = 2.5 kJ mol−1). These values have no precedent when using standard symmetrical containers and they pave the way for programming metal alternation in luminescent lanthanidopolymers.
Introduction
Metal-containing (bio)organic polymers are of the utmost importance in actual daily life and have found a wealth of applications in tailor-made materials for energy storage and energy conversion,1 drug delivery,2 shape-memory systems,3 supported catalysts and organic conductors,4 smart photonic devices,5 and modern light-emitting diodes.6 In the absence of metal, rationalization of the organization of (bio)organic (co)polymers relies on micro-segregation events described by the Huggins–Flory theory of phase demixing,7 a model which has been recently extended for the programming of thermotropic liquid crystals.8 The introduction of open-shell transition metals within the polymeric backbone results in novel optical and magnetic properties that are not available in pure organic polymers.1–5 However, the multifaceted (supra)molecular interactions operating between the polymeric backbone and the metal are at the origin of major difficulties in mastering the formation of metallopolymers with respect to stability, organization, processability and reproducibility. These limitations are even amplified for lanthanidopolymers (i.e. lanthanide-containing polymers) because of the versatile coordination behavior of these metallic centers.5 In order to avoid this pitfall, coordination chemists have restricted the concept of metallopolymers to infinite crystalline assemblies made of anionic ligand strands and cationic nodes forming extended 3D-networks, originally referred to as Wolf-type III metallopolymers4 or coordination polymers,9 and nowadays often named metal–organic frameworks (MOFs).10 These infinite assemblies resemble ionic solids in their essence and lead to robust and inert scaffolds possessing variable porosities. When trivalent emissive lanthanides occupy some nodes of the network, the associated luminescence can be tuned by metal doping11 or by external stimuli such as temperature jumps or mechanical stress.12 However, the production of solvent-resistant lanthanidopolymers compatible with partial metal occupancy, specific organization, flexible shaping and adaptable sensing properties is not yet available. Current efforts exploit the empirical mixing of polymeric organic receptors with metallic salts, from which non-soluble adducts are isolated. Their limited reproducibility and difficult characterization13 severely restrict pertinent developments along this line. An alternative approach proposes to take advantage of the powerful toolkit of reversible thermodynamics that has been developed to unravel multiple protonations in linear polyelectrolytes,14 for the in-depth deciphering of the loading of linear polymeric multi-terdentate receptors P1N with neutral luminescent [Ln(hfa)3] complexes (Ln = trivalent lanthanide, hfa = hexafluoroacetylacetonate) in dichloromethane (Fig. 1a).15 In solution, lanthanide tris-betadiketonate complexes exist as Lewis base adducts [Ln(hfa)3X] where X is a solvent molecule or an additional donor atom borne by co-ligands. Upon reaction with the target binding site of a polymer, for instance P1N, only the core [Ln(hfa)3] is transferred (Fig. 1a). In order to use a single concept for the source [Ln(hfa)3X] and the transferable core [Ln(hfa)3], we use the term ‘neutral lanthanide container’ for describing these beta-diketonate coordination complexes. Using the site-binding model,14,16 complexation processes can be modeled using two simple parameters: (1) the free energy of the intermolecular affinity of the entering metal for one terdentate N3 site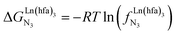 , which is the unique parameter to be considered for a monomeric unit and (2) the inter-site interaction energy
, which is the unique parameter to be considered for a monomeric unit and (2) the inter-site interaction energy 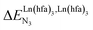 which accounts for modulations of the intrinsic affinity when multiple binding events operate in binuclear (or higher-order) linear receptors (i.e. cooperativity).17 Whereas major attention is usually focused on the maximization of host-guest affinities (i.e. minimizing
which accounts for modulations of the intrinsic affinity when multiple binding events operate in binuclear (or higher-order) linear receptors (i.e. cooperativity).17 Whereas major attention is usually focused on the maximization of host-guest affinities (i.e. minimizing 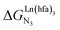 ), an instructed programming of
), an instructed programming of 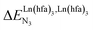 is more tricky since both negative (cooperative) or positive (anti-cooperative) issues are attractive for specific applications.
is more tricky since both negative (cooperative) or positive (anti-cooperative) issues are attractive for specific applications.
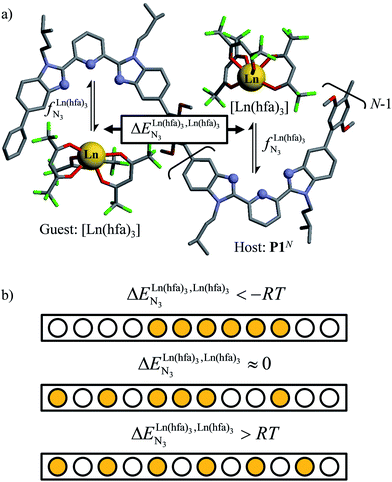 | ||
Fig. 1 (a) Thermodynamic model showing successive intermolecular connections of [Ln(hfa)3] to one-dimensional multi-terdentate receptors P1N (N = 10–30).15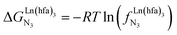 is the intrinsic intermolecular affinity and is the intrinsic intermolecular affinity and 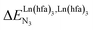 is the nearest-neighbor interaction (color code: C = grey, N = blue, O = red, F = green, Ln = orange). (b) Pictorial representation of the effect of intermetallic interactions on the microstates of a half-filled metallopolymer (orange disc = occupied site, white disc = empty site). is the nearest-neighbor interaction (color code: C = grey, N = blue, O = red, F = green, Ln = orange). (b) Pictorial representation of the effect of intermetallic interactions on the microstates of a half-filled metallopolymer (orange disc = occupied site, white disc = empty site). | ||
For instance, metal clustering compatible with efficient short-range intermetallic communication and energy migration18 results when 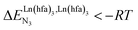 (cooperative process, top of Fig. 1b). In contrast, metal alternation produced by anti-cooperative processes (
(cooperative process, top of Fig. 1b). In contrast, metal alternation produced by anti-cooperative processes (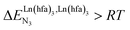 , bottom of Fig. 1b) in half-filled linear metallopolymers is appealing for applications in drug sensing,19 light-upconversion20 and metal segregation.21 Finally,
, bottom of Fig. 1b) in half-filled linear metallopolymers is appealing for applications in drug sensing,19 light-upconversion20 and metal segregation.21 Finally, 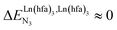 (middle of Fig. 1b) produces uncontrolled statistical metallic dispersion, a behavior found in most doped MOFs, and which is encountered for metallopolymers possessing large inter-site separations.14c The experimental magnitude of the inter-site interaction parameters
(middle of Fig. 1b) produces uncontrolled statistical metallic dispersion, a behavior found in most doped MOFs, and which is encountered for metallopolymers possessing large inter-site separations.14c The experimental magnitude of the inter-site interaction parameters 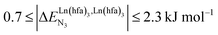 observed for the loading of polymers P1N with symmetrical [Ln(hfa)3] containers (Ln = Y, La, Eu and Lu, Fig. 1a) in dichloromethane did not exceed the average thermal energy (RT = 2.5 kJ mol−1), and therefore no organization could be induced on the macroscopic scale.15
observed for the loading of polymers P1N with symmetrical [Ln(hfa)3] containers (Ln = Y, La, Eu and Lu, Fig. 1a) in dichloromethane did not exceed the average thermal energy (RT = 2.5 kJ mol−1), and therefore no organization could be induced on the macroscopic scale.15
A recent focus17 on a family of monomeric L1 and dimeric model ligands L2–L4 (Fig. 2) demonstrated that (i) the intrinsic affinities 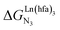 exponentially decrease with the number of binding sites, (ii) the inter-site interactions
exponentially decrease with the number of binding sites, (ii) the inter-site interactions 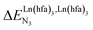 are affected by the relative geometries of the binding sites and (iii) minor changes in solvation processes, well described by the Onsager equation,22 are responsible for the tuning of these thermodynamic parameters. With these theoretical toolkits in hand, we suspect that the successive fixation of unsymmetrical lanthanide containers [Ln(tfa)3], [Ln(pta)3], [Ln(tta)3] and [Ln(pbta)3], instead of symmetrical [Ln(hfa)3] (Fig. 3), could provide magnified anti-cooperative processes.17 Taking the same set of ligands L1–L4 as a proof-of-concept, we report here that unsymmetrical [Ln(pbta)3] follows the predicted trend and exhibits, to the best of our knowledge, the largest intermetallic inter-site interactions ever quantified for neutral polynuclear lanthanide complexes.
are affected by the relative geometries of the binding sites and (iii) minor changes in solvation processes, well described by the Onsager equation,22 are responsible for the tuning of these thermodynamic parameters. With these theoretical toolkits in hand, we suspect that the successive fixation of unsymmetrical lanthanide containers [Ln(tfa)3], [Ln(pta)3], [Ln(tta)3] and [Ln(pbta)3], instead of symmetrical [Ln(hfa)3] (Fig. 3), could provide magnified anti-cooperative processes.17 Taking the same set of ligands L1–L4 as a proof-of-concept, we report here that unsymmetrical [Ln(pbta)3] follows the predicted trend and exhibits, to the best of our knowledge, the largest intermetallic inter-site interactions ever quantified for neutral polynuclear lanthanide complexes.
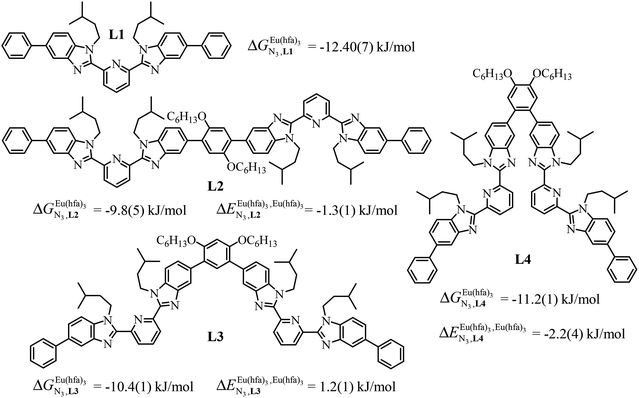 | ||
Fig. 2 Chemical structures of ligands L1–L4 gathering the thermodynamic intermolecular affinities 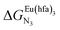 and nearest-neighbor interactions and nearest-neighbor interactions 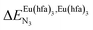 for their loading with [Eu(hfa)3] (CD2Cl2, 298 K). for their loading with [Eu(hfa)3] (CD2Cl2, 298 K). | ||
Results and discussion
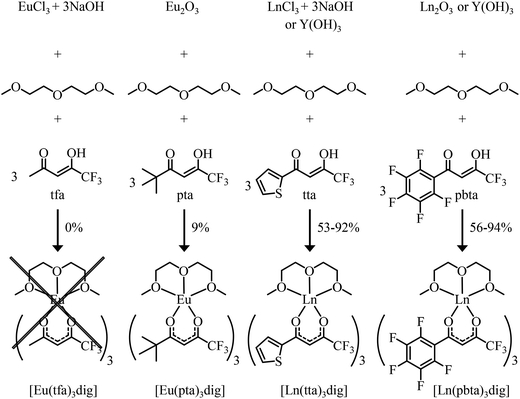
Synthesis and characterization of unsymmetrical neutral lanthanide containers [Ln(tfa)3dig], [Ln(pta)3dig], [Ln(tta)3dig] and [Ln(pbta)3dig]
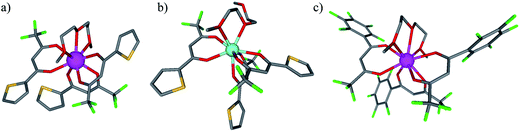
The desired unsymmetrical lanthanide containers were synthesised following the strategy developed for [Ln(hfa)3dig].23 Bis(2-methoxyethyl)ether (diglyme = dig) was added to a suspension of either lanthanide oxide Ln2O3, hydroxide Ln(OH)3·xH2O or chloride LnCl3·xH2O (combined with 3 eq. NaOH) in aprotic solvent (CH2Cl2, hexane or toluene) followed by the addition of the pertinent β-diketonate ligand. Purification by crystallisation or sublimation provided the target products [Ln(X)3dig] (X = pta, tta and pbta) in various yields (Fig. 3 and Appendix 1 in the ESI†). The europium container [Eu(tfa)3dig] could not be obtained and the reaction stopped with the formation of Eu(tfa)3·xH2O, probably because the bound anionic diketonate ligands are too strong as donors for releasing sufficient residual positive charge on the lanthanide for further complexation with neutral diglyme. A similar limitation was encountered with pivaloyl-trifluoroacetone (pta) ligands, for which tricky sublimations of intricate mixtures provided only 9% of the target product [Eu(pta)3dig]. The remaining electron-deficient β-diketonate ligands, tta and pbta, gave [Ln(tta)3dig] and [Ln(pbta)3dig] (Ln = La, Eu, and Y) in moderate (Ln = Y) to good (Ln = Eu and La) yields.The 1H and 19F-NMR spectra confirm the formation of pseudo-C3 species in solution, which are dynamic on the NMR time scale (Fig. 4 and S1–S4 in the ESI†).24 Elemental analyses of the microcrystalline powders point to the formation of unsolvated [Ln(β-diketonate)3dig] adducts (Appendix 1), a trend confirmed by the X-ray crystal structures solved for [Eu(tta)3dig] (1), [Y(tta)3dig] (2) and [Eu(pbta)3dig] (3) (Fig. 5, S4–S6 and Tables S1–S13†). All bond lengths in the europium complexes [Eu(tta)3dig] (1) and [Eu(pbta)3dig] (3) are within the standard range and are comparable to those reported for symmetrical [Eu(hfa)3dig] (Table S13†),25 a trend in line with similar affinities displayed by any of the fluorinated β-diketonate ligands (hfa−, tta− and pbta−) for the central trivalent cation.
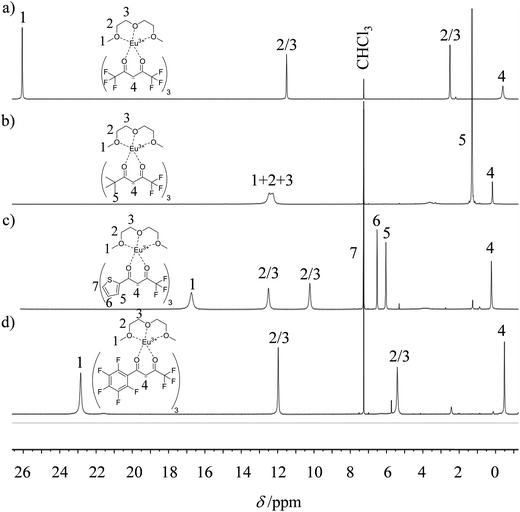 | ||
| Fig. 4 1H NMR spectra of europium-containing lanthanide containers (a) [Eu(hfa)3dig], (b) [Eu(pta)3dig], (c) [Eu(tta)3dig] and (d) [Eu(pbta)3dig] with numbering scheme (CDCl3, 298 K). | ||
Subject to SHAPE26 analysis, the EuO9 coordination spheres correspond best to monocapped square antiprisms with the central oxygen donor of the diglyme ligand occupying the capping position (Fig. S7a†). The smaller size of trivalent yttrium leads to eight-coordination in [Y(tta)3dig] (2) where the diglyme acts as a bidentate ligand (Fig. 5b). The eight bound oxygen atoms occupy the vertices of an approximate square antiprism,26 a trend in line with quantum chemical calculations performed on [Y(tta)3(H2O)x] in the gas-phase.27 Compared with [Eu(tta)3dig] (Fig. 5a), two tta diketonate ligands are significantly twisted in [Y(tta)3dig] (Fig. S8†). All bond valences significantly increase as a result of the larger residual charge carried by the eight-coordinate YIII (Table S13†). The electric dipole moments computed for the gas-phase optimised geometries (Fig. S7b†) roughly point along the Ln–Ocentral(diglyme) bond direction and decrease in the order hfa (7.7 D) > pbta (6.7 D) > tta (4.6 D), a tendency which contrasts with pioneer calculations performed for six-coordinate [Ln(β-diketonate)3] systems28 and with chemical intuition, which naively associates larger dipole moments with unsymmetrical β-diketonate ligands. We conclude that the magnitudes of the dipole moments in [LnX3dig] are indeed controlled by the residual positive charge borne by the trivalent lanthanide, which increases with the electron-withdrawing effect of the bound β-diketonate ligands (hfa > pbta ≫ tta).
Thermodynamic loading of the terdentate ligand L1 with the unsymmetrical neutral lanthanide containers [Ln(pta)3dig], [Ln(tta)3dig] and [Ln(pbta)3dig]: a strategy for addressing intrinsic intermolecular affinities
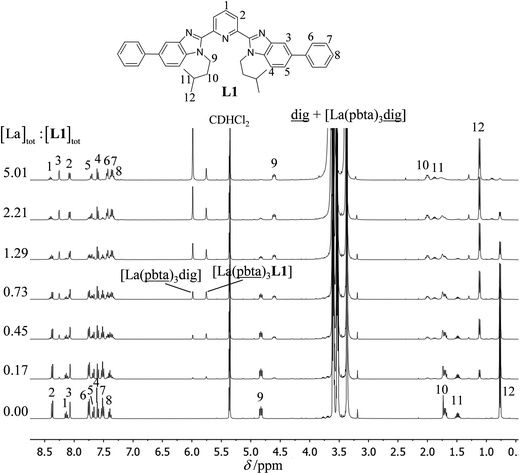
The 1H NMR titrations of 10 mm of the monomeric terdentate ligand L1 with [LnX3dig] (Ln = La, Eu, and Y; X = pta, tta and pbta; dig = diglyme) conducted in dichloromethane containing an excess of diglyme ([dig]tot = 0.14 m) show the formation of a single adduct [LnX3L1] complex according to eqn (1) (Fig. 6 and Tables S14 and S15†).15a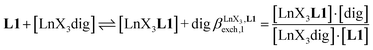 | (1) |
Since the total concentration of diglyme does not significantly vary, the stability constant 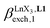 associated with the ligand exchange process depicted in eqn (1) reduces to the conditional association constant
associated with the ligand exchange process depicted in eqn (1) reduces to the conditional association constant 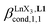 summarized in eqn (2), where
summarized in eqn (2), where 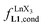 is the conditional affinity factor of a terdentate site for a [LnX3] container (Fig. 1a).15a
is the conditional affinity factor of a terdentate site for a [LnX3] container (Fig. 1a).15a
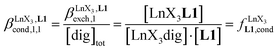 | (2) |
Experimentally, the integrations of the 1H NMR signals recorded for a given proton connected either to the free ligand L1 (IL1H) or to the coordinate ligand in [LnX3L1] 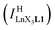 can be combined to determine the occupancy factor θLnL1 (left part of eqn (3)), which is related to the association constant
can be combined to determine the occupancy factor θLnL1 (left part of eqn (3)), which is related to the association constant 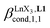 via the Langmuir binding isotherm (right part of eqn (3)).15a
via the Langmuir binding isotherm (right part of eqn (3)).15a
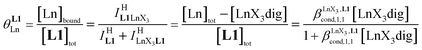 | (3) |
Repeating this procedure for different 〈[L1]tot;[Ln]tot〉 ratios (Fig. 6) yields occupancy factors θLnL1 (eqn (3), left) for various free concentrations of the lanthanide container [LnX3dig] (eqn (3), middle). Plots of θLnL1 related to log([LnX3dig]) (Fig. 7), often referred to as binding isotherms, are fit to eqn (3) (right part) using non-linear least-square techniques to give the conditional association constant 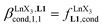 collected in Table S16† and the intrinsic exchange affinities
collected in Table S16† and the intrinsic exchange affinities 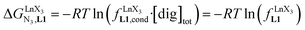 depicted in Fig. 8.
depicted in Fig. 8.
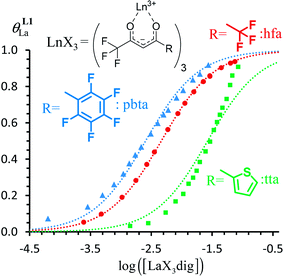 | ||
Fig. 7 Binding isotherms built from 1H NMR titrations of L1 with [LaX3dig] (X = hfa (red), tta (green) or pbta (blue)) in CD2Cl2 + 0.14 m dig at 293 K. The dotted traces correspond to the fitted curves computed with eqn (3) and using 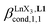 collected in Table S16.† collected in Table S16.† | ||
For the unsymmetrical perfluorobenzene-trifluoroacetylacetonate lanthanide containers [Ln(pbta)3dig] (Ln = La, Eu, and Y, the blue traces in Fig. 7 and 8), the intrinsic exchange affinities 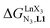 (eqn (1)) increase by 8–14% with respect to those found for the famous symmetrical [Ln(hfa)3dig] analogues (red traces in Fig. 7 and 8). For the unsymmetrical, but less electron-deficient thienyl-trifluoroacetylacetonato lanthanide containers [Ln(tta)3dig] (Ln = La, Eu, and Y, the green traces in Fig. 7 and 8), the affinity for L1 is still detectable, but low enough when Ln = Y for providing fast exchange on the NMR scale. In these conditions, the monitoring of a single broadened 1H NMR signal δHobs for each proton in solution during the titration prevents the use of eqn (3), which is replaced by eqn (4) for estimating the occupancy factor θYL1 (δL1H and
(eqn (1)) increase by 8–14% with respect to those found for the famous symmetrical [Ln(hfa)3dig] analogues (red traces in Fig. 7 and 8). For the unsymmetrical, but less electron-deficient thienyl-trifluoroacetylacetonato lanthanide containers [Ln(tta)3dig] (Ln = La, Eu, and Y, the green traces in Fig. 7 and 8), the affinity for L1 is still detectable, but low enough when Ln = Y for providing fast exchange on the NMR scale. In these conditions, the monitoring of a single broadened 1H NMR signal δHobs for each proton in solution during the titration prevents the use of eqn (3), which is replaced by eqn (4) for estimating the occupancy factor θYL1 (δL1H and 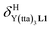 stand for the chemical shifts of the same proton in pure L1 and [Y(tta)3L1], respectively).
stand for the chemical shifts of the same proton in pure L1 and [Y(tta)3L1], respectively).
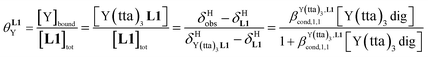 | (4) |
For these [Ln(tta)3] containers, occupancy factors larger than 20% are only obtained in a large excess of [Ln(tta)3dig], the total concentrations of which may reach 0.1 M in solution. The express requisite for using an invariant total concentration of diglyme in eqn (2) is no more obeyed and deviations from simple Langmuir isotherms are observed (green trace in Fig. 7). The conditional association constants reported for [Ln(tta)3L1] complexes are therefore only mere estimations. Finally, the pyvaloyl-trifluoroacetylacetonate europium container [Eu(pta)3dig], which bears the lowest residual positive charge on the metal,29 displayed no measurable affinity for L1 in CD2Cl2 at millimolar concentrations, a result in line with the lack (to the best of our knowledge) of crystal structures reporting a nine-coordinate [Ln(pta)3L] adduct, where L is a terdentate chelate nitrogen donor ligand.30 Leaving pta-based complexes aside, pure [Ln(pbta)3L1] (Ln = La, Eu, and Y) and [Ln(tta)3L1] (Ln = La and Eu) complexes could be isolated as crystalline materials from concentrated solutions in 41–92% yield (Appendix 1, Tables S13, S14 and S17†). The crystal structure of [Eu(pbta)3L1]·CH2Cl2 (4) confirms nine-coordination around the europium cation by the three nitrogen atoms of the bound aromatic ligand and the six oxygen atoms of the three bidentate pbta anions (Fig. 9, Tables S18–S21 and Fig. S9†). The [EuN3O6] chromophore adopts a distorted monocapped square antiprism geometry,26 very similar to that previously described for [La(hfa)3L1] (Table S22 and Fig. S10†).15a
In conclusion, two strong electron-withdrawing groups per β-diketonate in hfa (two CF3 groups) or in pbta (CF3 and C6F5) are required in order to get intrinsic affinities 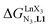 large enough to form significant amounts of [LnX3L1] at millimolar concentrations (Fig. 8, X represents the β-diketonate anion). The connections of less electron-withdrawing thenoyl (X = tta) or pivaloyl groups (X = pta) are detrimental in terms of the global stabilities of the adducts. This trend is correlated with the dipole moments computed for the gas-phase optimized [YX3L1] complexes, which reveal that the global asymmetry of the charge distribution increases along the series [Y(pbta)3L1] (μ = 13.1 D) ≈ [Y(hfa)3L1] (μ = 13.8 D) < [Y(tta)3L1] (μ = 14.9 D, Fig. S11†).
large enough to form significant amounts of [LnX3L1] at millimolar concentrations (Fig. 8, X represents the β-diketonate anion). The connections of less electron-withdrawing thenoyl (X = tta) or pivaloyl groups (X = pta) are detrimental in terms of the global stabilities of the adducts. This trend is correlated with the dipole moments computed for the gas-phase optimized [YX3L1] complexes, which reveal that the global asymmetry of the charge distribution increases along the series [Y(pbta)3L1] (μ = 13.1 D) ≈ [Y(hfa)3L1] (μ = 13.8 D) < [Y(tta)3L1] (μ = 14.9 D, Fig. S11†).
Thermodynamic loading of multi-terdentate ligands L2–L4 with unsymmetrical neutral lanthanide containers [Eu(tta)3dig] and [Eu(pbta)3dig]: a strategy for addressing nearest-neighbor interactions
A reliable analysis of the inter-site interactions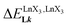 , which control the successive binding of two adjacent [LnX3] containers in linear multi-site receptors, requires the investigation of the dimeric receptors L2–L4 (eqn (5) and (6)), for which the cumulative conditional association constants
, which control the successive binding of two adjacent [LnX3] containers in linear multi-site receptors, requires the investigation of the dimeric receptors L2–L4 (eqn (5) and (6)), for which the cumulative conditional association constants 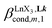 are given in eqn (7) and (8).
are given in eqn (7) and (8).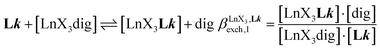 | (5) |
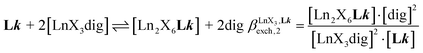 | (6) |
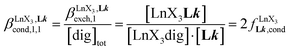 | (7) |
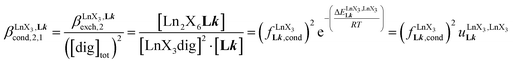 | (8) |
According to the site binding model,16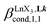 (eqn (7)) reflects the intrinsic binding affinity of the lanthanide container for a single terdentate site, but modulated by a statistical factor of 2 in a dimer. With this in mind,
(eqn (7)) reflects the intrinsic binding affinity of the lanthanide container for a single terdentate site, but modulated by a statistical factor of 2 in a dimer. With this in mind, 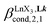 (eqn (8)) easily provides an estimation of the inter-site interactions measured as their Boltzmann factors
(eqn (8)) easily provides an estimation of the inter-site interactions measured as their Boltzmann factors 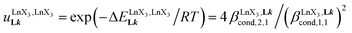 , a parameter often referred to as the allosteric cooperativity factor.31 As the intrinsic affinity of [Ln(tta)3dig] for the terdentate binding unit is too weak to produce significant quantities of the binuclear [Ln2(tta)6Lk] complexes at millimolar concentrations, the thermodynamic studies performed on the symmetrical [Eu2(hfa)6Lk] dimers17 are completed here with the recording of 1H and 19F NMR spectra for the complexation of L2–L4 (5 mm) with [Eu(pbta)3dig] in CD2Cl2 + 0.14 m diglyme (Fig. S12†). The integrations of the various signals (IH and IF) gave occupancy factors (eqn (9) and Fig. 10), which could be fitted to eqn (10) to get the intrinsic affinities
, a parameter often referred to as the allosteric cooperativity factor.31 As the intrinsic affinity of [Ln(tta)3dig] for the terdentate binding unit is too weak to produce significant quantities of the binuclear [Ln2(tta)6Lk] complexes at millimolar concentrations, the thermodynamic studies performed on the symmetrical [Eu2(hfa)6Lk] dimers17 are completed here with the recording of 1H and 19F NMR spectra for the complexation of L2–L4 (5 mm) with [Eu(pbta)3dig] in CD2Cl2 + 0.14 m diglyme (Fig. S12†). The integrations of the various signals (IH and IF) gave occupancy factors (eqn (9) and Fig. 10), which could be fitted to eqn (10) to get the intrinsic affinities 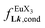 and cooperativity factors
and cooperativity factors 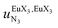 collected in Fig. 11 (Table S23†).
collected in Fig. 11 (Table S23†).
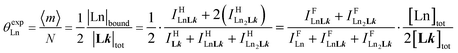 | (9) |
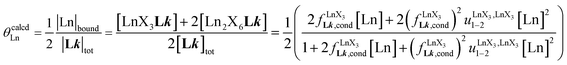 | (10) |
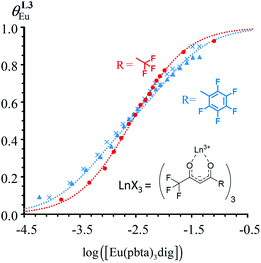 | ||
Fig. 10 Occupancy factors and binding isotherms built from NMR titrations of L3 with [Eu(hfa)3dig] (red disks, 1H NMR)17 and [Eu(pbta)3dig] (blue triangles for 1H NMR, blue crosses for 19F NMR) in CD2Cl2 + 0.14 m dig at 298 K. The dotted traces correspond to the fitted curves computed with eqn 10 and using 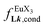 and and 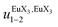 collected in Table S23.† collected in Table S23.† | ||
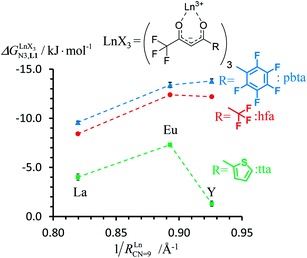
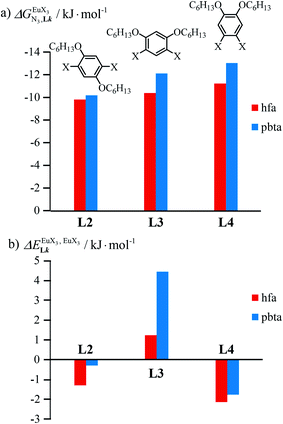
In line with the trend observed for the monomeric ligand L1 (Fig. 8), the intrinsic affinities of a terdentate unit in the dimeric ligands L2–L4 are roughly 10% larger for [Eu(pbta)3dig] than for [Eu(hfa)3dig] (Fig. 11a). The observed intermetallic interactions 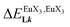 are systematically shifted toward more anti-cooperative processes for [Eu2(pbta)6Lk] complexes (Fig. 11b).
are systematically shifted toward more anti-cooperative processes for [Eu2(pbta)6Lk] complexes (Fig. 11b).
This drift culminates for [Eu2(pbta)6L3], in which the anti-cooperative interaction between the two unsymmetrical [Eu(pbta)3] containers amounts to almost +5 kJ mol−1, a value which should prevent a statistical redistribution due to thermal energy in half-filled linear polymers integrating this bis-terdentate structural motif. Considering that (i) the intermetallic distances are similar in the structures of [Eu2(hfa)3L3] (Eu⋯Eu = 12.61 Å in its crystal structure)17 and [Eu2(pbta)3L3] and (ii) the dipole moment calculated for [Y(pbta)3L1] is only slightly smaller than that found for [Eu(hfa)3L1] (Fig. S11†), we assign the gain in intermetallic repulsion by a factor of 3.7(6), going from [Eu2(hfa)3L3] (symmetrical β-diketonate) to [Eu2(pbta)3L3] (unsymmetrical β-diketonate), to specific solvation effects which are known to largely dominate over the minor contributions produced by intramolecular dipole–dipole interactions.17
Photophysical properties and luminescence quantum yields of the europium containers [EuX3(dig)] (X = hfa, tta, pbta) and of their mononuclear [EuX3L1] and binuclear [Eu2(hfa)6Lk] complexes (Lk = L2–L4)
The electronic absorption spectra of the europium containers [EuX3(dig)] (X = hfa, tta, and pbta) are dominated by β-diketonate-centred π* ← π transitions occurring in the near-UV range (dotted traces in Fig. 12 and S13†). The maximum of the absorption envelope is shifted stepwise toward lower energy upon the replacement of the trifluoromethyl substituents found in [Eu(hfa)3dig] (33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 cm−1, Fig. S13†) with aromatic groups in [Eu(pbta)3dig] (32
100 cm−1, Fig. S13†) with aromatic groups in [Eu(pbta)3dig] (32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 for one pentafluorobenzene unit, Fig. 12b) and [Eu(tta)3dig] (30
000 cm−1 for one pentafluorobenzene unit, Fig. 12b) and [Eu(tta)3dig] (30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 for one thenoyl unit, Fig. 12a). Exchanging the saturated diglyme ligand with the aromatic terdentate ligand L1 in [EuX3L1] provides absorption spectra (full traces in Fig. 12) which combine the contributions of each individual chromophore, i.e. the β-diketonate-centred π* ← π transitions (dotted traces in Fig. 12) together with L1-centered
000 cm−1 for one thenoyl unit, Fig. 12a). Exchanging the saturated diglyme ligand with the aromatic terdentate ligand L1 in [EuX3L1] provides absorption spectra (full traces in Fig. 12) which combine the contributions of each individual chromophore, i.e. the β-diketonate-centred π* ← π transitions (dotted traces in Fig. 12) together with L1-centered 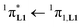 and
and 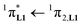 transitions (dashed traces in Fig. 12).32 Room-temperature excitations (
transitions (dashed traces in Fig. 12).32 Room-temperature excitations (![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) exc = 26
exc = 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–30
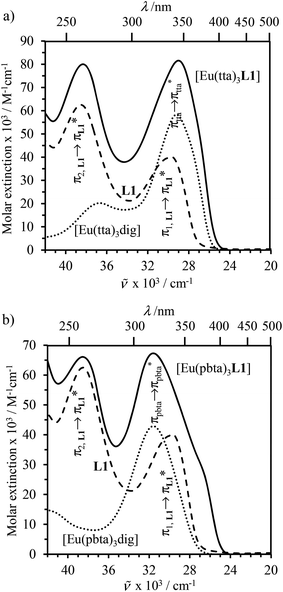
000–30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1) of the [EuX3dig] or [EuX3L1] complexes (X = hfa, tta, and pbta) in solution (Fig. 13 and S14†) or in the solid state (Fig. S15 and S16†) produce typical europium-centred red luminescence, which results from indirect sensitization according to the antenna mechanism.34 The initial ligand-centred 1π* ← 1π excitation is followed by a (probable)35 intersystem crossing process, then L1 → Eu and/or X → Eu energy transfers occur, thus leading to Eu(5D1) and Eu(5D0)-centred emissions.34,35 The europium-centred emission bands recorded for [EuX3dig] and [EuX3L1] are diagnostic for the existence of low-symmetry tris-β-diketonates Eu(III) complexes with (i) Eu(5D1 → 7FJ) emissions being far less intense than for Eu(5D0 → 7FJ)15a,33 and (ii) Eu(5D0 → 7FJ) emissions being dominated by the 2J + 1 = 5 split components of the hypersensitive forced electric dipolar 5D0 → 7F2 transition monitored around 16
000 cm−1) of the [EuX3dig] or [EuX3L1] complexes (X = hfa, tta, and pbta) in solution (Fig. 13 and S14†) or in the solid state (Fig. S15 and S16†) produce typical europium-centred red luminescence, which results from indirect sensitization according to the antenna mechanism.34 The initial ligand-centred 1π* ← 1π excitation is followed by a (probable)35 intersystem crossing process, then L1 → Eu and/or X → Eu energy transfers occur, thus leading to Eu(5D1) and Eu(5D0)-centred emissions.34,35 The europium-centred emission bands recorded for [EuX3dig] and [EuX3L1] are diagnostic for the existence of low-symmetry tris-β-diketonates Eu(III) complexes with (i) Eu(5D1 → 7FJ) emissions being far less intense than for Eu(5D0 → 7FJ)15a,33 and (ii) Eu(5D0 → 7FJ) emissions being dominated by the 2J + 1 = 5 split components of the hypersensitive forced electric dipolar 5D0 → 7F2 transition monitored around 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 320 cm−1 (Fig. 13 and S14†).36 Only minor changes can be detected in terms of the relative intensities, splitting and energies for the Eu(5D0 → 7FJ) transitions when the diglyme in [EuX3dig] is replaced with L1 in [EuX3L1]. However, the global quantum yields ΦLEu, recorded upon UV-irradiation of the ligands while measuring the Eu-centered emission, rise by factors of 2 to 10 going from [EuX3dig] (3% ≤ ΦLEu ≤ 10%) to [EuX3L1] (22% ≤ ΦLEu ≤ 45%, Table S24†). These considerable global quantum yields are typical among tris-β-diketonate complexes, for which a systematic optimization may lead to 40–70% quantum yield values.24,37
320 cm−1 (Fig. 13 and S14†).36 Only minor changes can be detected in terms of the relative intensities, splitting and energies for the Eu(5D0 → 7FJ) transitions when the diglyme in [EuX3dig] is replaced with L1 in [EuX3L1]. However, the global quantum yields ΦLEu, recorded upon UV-irradiation of the ligands while measuring the Eu-centered emission, rise by factors of 2 to 10 going from [EuX3dig] (3% ≤ ΦLEu ≤ 10%) to [EuX3L1] (22% ≤ ΦLEu ≤ 45%, Table S24†). These considerable global quantum yields are typical among tris-β-diketonate complexes, for which a systematic optimization may lead to 40–70% quantum yield values.24,37
More precisely, we note that the quantum yield ΦLEu = 5(1)% obtained here for [Eu(hfa)3dig] in dichloromethane is much lower than ΦLEu = 35% reported for the same complex in ether![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) isopentane
isopentane![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ethanol (5
ethanol (5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2).38 In contrast, those obtained for [EuX3L1] in the solid state (15–40%) are in line with ΦLEu = 20–30% previously reported for closely related [Eu(hfa)3L] complexes where L is a terdentate N-donor ligand.33 Although no detailed separation of radiative and non-radiative contributions to the various rate constants implied by the antenna mechanism are currently available, the observed mono-exponential millisecond range Eu(5D0) lifetimes (Table S24†) reveal a reasonable protection of the Eu(III) emissive center against the harmonics of high-energy oscillators in these unsymmetrical complexes. Finally, the introduction of bis(hexyloxy)phenyl spacers in the binuclear complexes [Eu2(hfa)6Lk] (Lk = L2–L4) has a deleterious effect on the global quantum yields, which are reduced by one order of magnitude (2% ≤ ΦLEu ≤ 5%) regarding those collected for the mononuclear analogues [Eu(hfa)3Lk]. This specific effect was previously documented for related binuclear europium complexes35a and unambiguously assigned to a drastic reduction of the Lk → Eu(III) energy transfer rate constants when electron-donor groups are connected to the phenyl spacers. Our overview of the luminescence properties of [EuX3dig], [Eu(hfa)3L1] and [Eu2(hfa)6Lk] confirms that the replacement of symmetrical X = hfa ligands with unsymmetrical β-diketonate analogues (X = tta and pbta) does not dramatically impact the global photophysical properties of these complexes, which remain highly luminescent and therefore compatible with the preparation of strong red emissive lanthanidopolymers assuming that the thermodynamic metal loading is under control.
2).38 In contrast, those obtained for [EuX3L1] in the solid state (15–40%) are in line with ΦLEu = 20–30% previously reported for closely related [Eu(hfa)3L] complexes where L is a terdentate N-donor ligand.33 Although no detailed separation of radiative and non-radiative contributions to the various rate constants implied by the antenna mechanism are currently available, the observed mono-exponential millisecond range Eu(5D0) lifetimes (Table S24†) reveal a reasonable protection of the Eu(III) emissive center against the harmonics of high-energy oscillators in these unsymmetrical complexes. Finally, the introduction of bis(hexyloxy)phenyl spacers in the binuclear complexes [Eu2(hfa)6Lk] (Lk = L2–L4) has a deleterious effect on the global quantum yields, which are reduced by one order of magnitude (2% ≤ ΦLEu ≤ 5%) regarding those collected for the mononuclear analogues [Eu(hfa)3Lk]. This specific effect was previously documented for related binuclear europium complexes35a and unambiguously assigned to a drastic reduction of the Lk → Eu(III) energy transfer rate constants when electron-donor groups are connected to the phenyl spacers. Our overview of the luminescence properties of [EuX3dig], [Eu(hfa)3L1] and [Eu2(hfa)6Lk] confirms that the replacement of symmetrical X = hfa ligands with unsymmetrical β-diketonate analogues (X = tta and pbta) does not dramatically impact the global photophysical properties of these complexes, which remain highly luminescent and therefore compatible with the preparation of strong red emissive lanthanidopolymers assuming that the thermodynamic metal loading is under control.
Conclusion
In line with theoretical predictions,17 the replacement of symmetrical X = hfa with unsymmetrical X = tta or X = pbta β-diketonates in nine-coordinate neutral [LnX3dig] lanthanide containers induces major changes in the thermodynamic loading of terdentate N3 binding units. For both monomeric [LnX3L1] and dimeric [Eu2X6Lk] complexes (Lk = L2–L4), the intrinsic affinity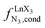 depends on the residual positive charge borne by the metal. It increases in the order
depends on the residual positive charge borne by the metal. It increases in the order 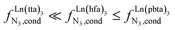 , which matches the electron-withdrawing character of the substituent groups located in the β-diketonate ligand (Fig. 8 and 11a). The supplementary inter-site repulsion operating in the dinuclear [Eu2X6Lk] complexes (Lk = L2–L4) is greatest for [Eu2(pbta)6L3] (Fig. 11b) with a remarkable anti-cooperative factor of
, which matches the electron-withdrawing character of the substituent groups located in the β-diketonate ligand (Fig. 8 and 11a). The supplementary inter-site repulsion operating in the dinuclear [Eu2X6Lk] complexes (Lk = L2–L4) is greatest for [Eu2(pbta)6L3] (Fig. 11b) with a remarkable anti-cooperative factor of 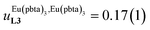 , which translates into a repulsive free energy of
, which translates into a repulsive free energy of 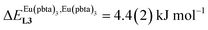 . The latter value is almost twice as large as the room temperature thermal energy.
. The latter value is almost twice as large as the room temperature thermal energy.
Assuming a thought experiment in which (i) a linear infinite polymer P2N (N → ∞) based on the meta-substituted phenyl spacers, as found in L3, is at hand (Fig. 14 top), and (ii) the anti-cooperative factors 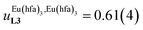 and
and 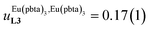 found for L3 similarly operate in P2N, the cluster expansion techniques14 predict the appearance of an unprecedented identifiable ‘plateau’ in the binding isotherm of the potential unsymmetrical linear {[Eu(pbta)3]mP2N} lanthanidopolymer (N → ∞, full red trace in Fig. 14), while its symmetrical analogue {[Eu(hfa)3]mP2N} would exhibit only the standard stochastic distributions of metal ions (dashed black trace in Fig. 14). In other words, a predictable |P2N|tot/|Eu(pbta)3|tot stoichiometric ratio should provide an inflection point at θEu = 0.5, where the half-filled polymer {[Eu(pbta)3]N/2P2N} is dominated by the formation of a microspecies, in which metal-occupied sites and metal-free sites strictly alternate (Fig. 1b bottom). The exact physical origin of this beneficial anti-cooperative effect remains elusive in the absence of quantitative access to solvation energies39 and Born–Haber cycles,17,22,40 but computational efforts are underway for unravelling the conditions required for exploiting this unprecedented effect for the preparation of highly organized metallopolymers.
found for L3 similarly operate in P2N, the cluster expansion techniques14 predict the appearance of an unprecedented identifiable ‘plateau’ in the binding isotherm of the potential unsymmetrical linear {[Eu(pbta)3]mP2N} lanthanidopolymer (N → ∞, full red trace in Fig. 14), while its symmetrical analogue {[Eu(hfa)3]mP2N} would exhibit only the standard stochastic distributions of metal ions (dashed black trace in Fig. 14). In other words, a predictable |P2N|tot/|Eu(pbta)3|tot stoichiometric ratio should provide an inflection point at θEu = 0.5, where the half-filled polymer {[Eu(pbta)3]N/2P2N} is dominated by the formation of a microspecies, in which metal-occupied sites and metal-free sites strictly alternate (Fig. 1b bottom). The exact physical origin of this beneficial anti-cooperative effect remains elusive in the absence of quantitative access to solvation energies39 and Born–Haber cycles,17,22,40 but computational efforts are underway for unravelling the conditions required for exploiting this unprecedented effect for the preparation of highly organized metallopolymers.
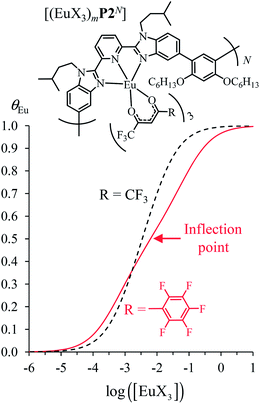 | ||
Fig. 14 Occupancy factors and binding isotherms computed for the loading of polymer P2N (N → ∞) in CH2Cl2 + 0.14 m diglyme at 293 K with [Eu(hfa)3dig] (dotted black trace, 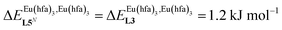 , Table S23†) and [Eu(pbta)3dig] (full red trace, , Table S23†) and [Eu(pbta)3dig] (full red trace, 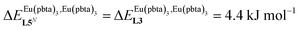 , Table S23†). , Table S23†). | ||
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The Swiss National Science Foundation is gratefully acknowledged for financial support. The work performed in France was supported by La Ligue contre le Cancer, Cancéropôle Grand Ouest and INSERM.References
- A. Winter and U. S. Schubert, Chem. Soc. Rev., 2016, 45, 5311–5357 RSC.
- Y. Yan, J. Zhang, L. Ren and C. Tang, Chem. Soc. Rev., 2016, 45, 5232–5263 RSC.
- C.-L. Ho and W.-Y. Wong, Coord. Chem. Rev., 2011, 255, 2469–2502 CrossRef CAS.
- (a) M. O. Wolf, Adv. Mater., 2001, 13, 545–553 CrossRef CAS; (b) M. O. Wolf, J. Inorg. Organomet. Polym. Mater., 2006, 16, 189–199 CrossRef CAS.
- J. M. Stanley and B. J. Holliday, Coord. Chem. Rev., 2012, 256, 1520–1530 CrossRef CAS.
- (a) J. Kido and Y. Okamoto, Chem. Rev., 2002, 102, 2357–2368 CrossRef CAS PubMed; (b) A. de Bettencourt-Dias, Dalton Trans., 2007, 2229–2241 RSC; (c) K. Binnemans, Chem. Rev., 2009, 109, 4283–4374 CrossRef CAS PubMed.
- (a) M. L. Huggins, J. Chem. Phys., 1941, 9, 440 CrossRef CAS; (b) P. J. Flory, J. Chem. Phys., 1941, 9, 660–661 CrossRef CAS; (c) Polymer Blends, ed. D. R. Paul and S. Newman, Academic Press, New York, San Francisco, London, 1978, vol. 2, pp. 25–32 and 116-121 Search PubMed.
- (a) C. Tschierske, Ann. Rep. Progr. Chem. Ser. C, 2001, 97, 191–267 RSC; (b) E. Bialecka-Florjanczyk, J. Phys. Chem. B, 2006, 110, 2582–2592 CrossRef CAS PubMed; (c) C. Tschierske, Top. Curr. Chem., 2012, 318, 1–108 CAS.
- (a) R. W. Corkery, Curr. Opin. Colloid Interface Sci., 2008, 13, 288–302 CrossRef CAS; (b) J. Heine and K. Müller-Buschbaum, Chem. Soc. Rev., 2013, 42, 9232–9242 RSC.
- (a) T. R. Cook, Y.-R. Zheng and P. J. Stang, Chem. Rev., 2012, 113, 734–777 CrossRef PubMed; (b) Y. Cui, Y. Yue, G. Qian and B. Chen, Chem. Rev., 2012, 112, 1126–1162 CrossRef CAS PubMed; (c) Y. Cui, B. Chen and G. Qian, Coord. Chem. Rev., 2014, 273–274, 76–86 CrossRef CAS.
- O. Guillou, C. Daiguebonne, G. Calvez and K. Bernot, Acc. Chem. Res., 2016, 49, 844–856 CrossRef CAS PubMed.
- (a) J. B. Beck and S. J. Rowan, J. Am. Chem. Soc., 2003, 125, 13922–13923 CrossRef CAS PubMed; (b) D. Knapton, P. K. Iyer, S. J. Rowan and C. Weder, Macromolecules, 2006, 39, 4069–4075 CrossRef CAS.
- (a) D. A. Turchetti, P. C. Rodrigues, L. S. Berlim, C. Zanlorenzi, G. C. Faria, T. D. Z. Atvars, W.-H. Schreiner and L. C. Akcelrud, Synth. Met., 2012, 162, 35–43 CrossRef CAS; (b) S. Basak, Y. S. L. V. Narayana, M. Baumgarten, K. Müllen and R. Chandrasekar, Macromolecules, 2013, 46, 362–369 CrossRef CAS; (c) Y. S. L. V. Narayana, S. Basak, M. Baumgarten, K. Müllen and R. Chandrasekar, Adv. Funct. Mater., 2013, 23, 5875–5880 CrossRef CAS; (d) D. A. Turchetti, R. A. Domingues, C. Zanlorenzi, B. Nowacki, T. D. Z. Atvars and L. C. Akcelrud, J. Phys. Chem. C, 2014, 118, 30079–30086 CrossRef CAS; (e) S. Basak, M. A. Mohiddon, M. Baumgarten, K. Müllen and R. Chandrasekar, Sci. Rep., 2015, 5, 8406 CrossRef CAS PubMed; (f) A. de Bettencourt-Dias and J. S. K. Rossini, Inorg. Chem., 2016, 55, 9954–9963 CrossRef CAS PubMed.
- (a) M. Borkovec, B. Jönsson and G. J. M. Koper, Surf. Colloid Sci., 2001, 16, 99–339 Search PubMed; (b) G. Koper and M. Borkovec, J. Phys. Chem. B, 2001, 105, 6666–6674 CrossRef CAS; (c) M. Borkovec, J. Hamacek and C. Piguet, Dalton Trans., 2004, 4096–4105 RSC; (d) M. Borkovec, G. J. M. Koper and C. Piguet, Curr. Opin. Colloid Interface Sci., 2006, 11, 280–289 CrossRef CAS; (e) G. J. M. Koper and M. Borkovec, Polymer, 2010, 51, 5649–5662 CrossRef CAS.
- (a) L. Babel, T. N. Y. Hoang, H. Nozary, J. Salamanca, L. Guénée and C. Piguet, Inorg. Chem., 2014, 53, 3568–3578 CrossRef CAS PubMed; (b) T. N. Y. Hoang, Z. Wang, L. Babel, H. Nozary, M. Borkovec, I. Szilagyi and C. Piguet, Dalton Trans., 2015, 44, 13250–13260 RSC.
- J. Hamacek, M. Borkovec and C. Piguet, Chem.–Eur. J., 2005, 11, 5217–5226 CrossRef CAS PubMed.
- L. Babel, T. N. Y. Hoang, L. Guénée, C. Besnard, T. A. Wesolowski, M. Humbert-Droz and C. Piguet, Chem.–Eur. J., 2016, 22, 8113–8123 CrossRef CAS PubMed.
- (a) A. Nonat, M. Regueiro-Figueroa, D. Esteban-Gomez, A. de Blas, T. Rodriguez-Blas, C. Platas-Iglesias and L. J. Charbonnière, Chem.–Eur. J., 2012, 18, 8163–8173 CrossRef CAS PubMed; (b) A. Zaïm, S. V. Eliseeva, L. Guénée, H. Nozary, S. Petoud and C. Piguet, Chem.–Eur. J., 2014, 20, 12172–12182 CrossRef PubMed.
- (a) U. S. Schubert and M. Heller, Chem.–Eur. J., 2001, 7, 5253–5259 CrossRef; (b) B. Liu, Y. Bao, F. Du, H. Wang, J. Tian and R. Bai, Chem. Commun., 2011, 47, 1731–1733 RSC; (c) Y. Yan, J. Zhang, L. Ren and C. Tang, Chem. Soc. Rev., 2016, 45, 5232–5263 RSC.
- (a) C.-Y. Sun, X.-J. Zheng, X.-B. Chen and L.-P. Jin, Inorg. Chim. Acta, 2009, 362, 325–330 CrossRef CAS; (b) I. Hernandez, N. Pathumakanthar, P. B. Wyatt and W. P. Gillin, Adv. Mater., 2010, 22, 5356–5360 CrossRef CAS PubMed.
- (a) S. Hiraoka, M. Goda and M. Shionoya, J. Am. Chem. Soc., 2009, 131, 4592–4593 CrossRef CAS PubMed; (b) K. Uemura, Dalton Trans., 2017, 46, 5474–5492 RSC.
- (a) L. Onsager, J. Am. Chem. Soc., 1936, 58, 1486–1492 CrossRef CAS; (b) D. V. Matyushov, J. Chem. Phys., 2004, 120, 1375–1382 CrossRef CAS PubMed; (c) G. Schreckenbach, Chem.–Eur. J., 2017, 23, 3797–3803 CrossRef CAS PubMed.
- (a) W. J. Evans, D. G. Giarikos, M. A. Johnston, M. A. Greci and J. W. Ziller, J. Chem. Soc., Dalton Trans., 2002, 520–526 RSC; (b) G. Malandrino, R. Lo Nigro, I. L. Fragala and C. Benelli, Eur. J. Inorg. Chem., 2004, 500–509 CrossRef CAS; (c) G. Malandrino and I. L. Fragala, Coord. Chem. Rev., 2006, 250, 1605–1620 CrossRef CAS.
- C. Freund, W. Porzio, U. Giovanella, F. Vignali, M. Pasini, S. Destri, A. Mech, S. Di Pietro, L. Di Bari and P. Mineo, Inorg. Chem., 2011, 50, 5417–5429 CrossRef CAS PubMed.
- S.-J. Kang, Y. S. Jung and Y. S. Sohn, Bull. Korean Chem. Soc., 1997, 18, 75–80 CAS.
- SHAPE is a free software developed by M. Llunell, D. Casanova, J. Cirera, P. Alemany and S. Alvarez, available online at http://www.ee.ub.edu. For more information see (a) M. Pinsky and D. Avnir, Inorg. Chem., 1998, 37, 5575–5582 CrossRef CAS PubMed; (b) D. Casanova, J. Cirera, M. Llunell, P. Alemany, D. Avnir and S. Alvarez, J. Am. Chem. Soc., 2004, 126, 1755–1763 CrossRef CAS PubMed; (c) J. Cirera, E. Ruiz and S. Alvarez, Chem.–Eur. J., 2006, 12, 3162–3167 CrossRef CAS PubMed.
- V. Vallet, Z. Szabo and I. Grenthe, Dalton Trans., 2011, 40, 3154–3165 RSC.
- A. Y. Rogachev, A. V. Nemukhin, N. P. Kuzmina and D. V. Sevastyanov, Dokl. Chem., 2003, 389, 87–91 CrossRef CAS.
- G. F. Gagabe, K. Satoh and K. Sawada, Talanta, 2011, 84, 1047–1056 CrossRef CAS PubMed.
- (a) G. Richards, J. Osterwyk, J. Flikkema, K. Cobb, M. Sullivan and S. Swavey, Inorg. Chem. Commun., 2008, 11, 1385–1387 CrossRef CAS; (b) S. S. Dudar’, E. B. Sveshnikova and V. L. Ermolaev, Opt. Spectrosc., 2008, 104, 225–234 CrossRef; (c) Y. Hasegawa, S. Tamaki, S. Saitou, Z. Piskuła, H. Yajima, J. Noro and S. Lis, Inorg. Chim. Acta, 2009, 362, 3641–3647 CrossRef CAS; (d) M. R. Silva, P. Martin-Ramos, J. T. Coutinho, L. C. J. Pereira, V. Lavin, I. R. Martin, P. S. P. Silva and J. Martin-Gil, Dalton Trans., 2015, 44, 1264–1272 RSC.
- G. Ercolani and L. Schiaffino, Angew. Chem., Int. Ed., 2011, 50, 1762–1768 CrossRef CAS PubMed.
- (a) K. Nakamoto, J. Phys. Chem., 1960, 64, 1420–1425 CrossRef CAS; (b) C. Piguet, J.-C. G. Bünzli, G. Bernardinelli, C. Bochet and P. Froidevaux, J. Chem. Soc., Dalton Trans., 1995, 83–97 RSC; (c) S. Xu, J. E. T. Smith and J. M. Weber, Inorg. Chem., 2016, 55, 11937–11943 CrossRef CAS PubMed.
- A. Zaïm, H. Nozary, L. Guénée, C. Besnard, J.-F. Lemonnier, S. Petoud and C. Piguet, Chem.–Eur. J., 2012, 18, 7155–7168 CrossRef PubMed.
- (a) N. Sabbatini, M. Guardigli and I. Manet, in Handbook on the Physics and Chemistry of Rare Earths, ed. K. A. Gschneidner and L. Eyring, Elsevier Science, Amsterdam, 1996, vol. 23, pp. 69–120 Search PubMed; (b) H. F. Brito, O. M. L. Malta, M. C. F. C. Felinto and E. E. S. Teotonio, The Chemistry of Metal Enolates, ed. J. Zabicky, John Wiley & Sons,Ltd, Chichester, 2009, ch. 3, pp. 131–184 Search PubMed; (c) Y.-W. Yip, H. Wen, W.-T. Wong, P. A. Tanner and K.-L. Wong, Inorg. Chem., 2012, 51, 7013–7015 CrossRef CAS PubMed; (d) M. Räsänen, H. Takalo, J. Rosenberg, J. Mäkelä, K. Haapakka and J. Kankare, J. Lumin., 2014, 146, 211–217 CrossRef.
- (a) J.-F. Lemonnier, L. Guénée, C. Beuchat, T. A. Wesolowski, P. Mukherjee, D. H. Waldeck, K. A. Gogik, S. Petoud and C. Piguet, J. Am. Chem. Soc., 2011, 133, 16219–16234 CrossRef CAS PubMed; (b) E. Kasprzycka, V. A. Trush, V. M. Amirkhanov, L. Jerzykiewicz, O. L. Malta, J. Legendziewicz and P. Gawryszewska, Chem.–Eur. J., 2017, 23, 1318–1330 CrossRef CAS PubMed.
- (a) C. Görller-Walrand and K. Binnemans, in Handbook on the Physics and Chemistry of Rare Earths, ed. K. A. Gschneidner and L. Eyring, Elsevier Science, Amsterdam, 1996, vol. 23, pp. 121–283 Search PubMed; (b) G. F. de Sa, O. L. Malta, C. de Mello Donega, A. M. Simas, R. L. Longo, P. A. Santa-Cruz and E. F. da Silva Jr, Coord. Chem. Rev., 2000, 196, 165–195 CrossRef CAS; (c) N. M. Shavaleev, S. V. Eliseeva, R. Scopelliti and J.-C. G. Bünzli, Inorg. Chem., 2015, 54, 9166–9173 CrossRef CAS PubMed.
- (a) K. Binnemans, in Handbook on the Physics and Chemistry of Rare Earths, ed. K. A. Gschneidner, J.-C. G. Bünzli and V. K. Pecharsky, Elsevier, North Holland, Amsterdam, 2005, vol. 35, pp. 107–272 Search PubMed; (b) K. Miyata, Y. Hasegawa, K. Kuramochi, T. Nakagawa, T. Yokoo and T. Kawai, Eur. J. Inorg. Chem., 2009, 4777–4785 CrossRef CAS; (c) Z. Chen, F. Ding, F. Hao, M. Guan, Z. Bian, B. Ding and C. Huang, New J. Chem., 2010, 34, 487–494 RSC; (d) S. V. Eliseeva, D. N. Pleshkov, K. A. Lyssenko, L. S. Lepnev, J.-C. G. Bünzli and N. P. Kuzmina, Inorg. Chem., 2011, 50, 5137–5144 CrossRef CAS PubMed; (e) A. I. S. Silva, V. F. C. Santos, N. B. D. Lima, A. M. Simas and S. M. C. Gonçalves, RSC Adv., 2016, 6, 90934–90943 RSC.
- M. L. Bhaumik, J. Chem. Phys., 1964, 40, 3711–3715 CrossRef CAS.
- C. J. Cramer and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 760–768 CrossRef CAS PubMed.
- N. Shimokhina, A. Bronowska and S. W. Homans, Angew. Chem., Int. Ed., 2006, 45, 6374–6376 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 1551909–1551912. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7sc03710d |
| This journal is © The Royal Society of Chemistry 2018 |