Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The harpooning mechanism as evidenced in the oxidation reaction of the Al atom†
Fangfang
Li‡
a,
Changwu
Dong‡
ab,
Jun
Chen
 ac,
Jiaxing
Liu
a,
Fengyan
Wang
ac,
Jiaxing
Liu
a,
Fengyan
Wang
 *a and
Xin
Xu
*a
*a and
Xin
Xu
*a
aDepartment of Chemistry, Collaborative Innovation Centre of Chemistry for Energy Materials (iChEM), Shanghai Key Laboratory of Molecular Catalysts and Innovative Materials, Fudan University, Shanghai, 200433, P. R. China. E-mail: fengyanwang@fudan.edu.cn; xxchem@fudan.edu.cn
bEast China Sea Centre of Standard & Metrology (Technology), SOA, Shanghai, 201306, P. R. China
cCollege of Chemistry and Chemical Engineering, Collaborative Innovation Centre of Chemistry for Energy Materials (iChEM), Xiamen University, Xiamen, P. R. China
First published on 2nd November 2017
Abstract
The harpooning mechanism has long been proposed for elementary reaction dynamics involving metals. It is characterized by an initial electron transfer (ET) process from the metal to the oxidant molecule. For the titled reaction Al + O2, the ET distance can be predicted to be 2.6 Å by simply calculating the energy difference between the ionization energy of the Al atom and the electron affinity of the O2 molecule. Hereby we experimentally derived the maximum impact parameter bmax of 2.5 ± 0.2 Å for the titled reaction, in consistency with the predicted ET distance. This derivation of bmax was achieved by using the crossed molecular beam experiment at a collision energy of 507 cm−1 (i.e. 1.45 kcal mol−1) with a high resolution time-sliced ion velocity imaging detection of the state-selective AlO products based on the (1 + 1) resonance-enhanced multiphoton ionization. The small rotational constant of the AlO(X2Σ+) radical (Be = 0.6413 cm−1) facilitated the formation of the AlO(v = 0) products in high rotational levels up to the energetically limited state, Nmax = 52, with an almost zero velocity mapping. Hence, in this extreme angular momentum disposal case, the collisional orbital angular momentum l was nearly completely channeled into the product rotational angular momentum as a consequence of the conservations of energy and angular momentum, offering a reaction system that breaks the restriction of kinematically favored mass combination in order to obtain information on the impact parameters. The present study yields the first direct derivation of bmax from the maximum rotational level of products under the experimental condition with the recoil energy E′T ≈ 0. This, in turn, provides solid evidence in supporting the harpooning mechanism.
Introduction
The electron transfer (ET) process plays a fundamental role in many chemical systems.1 In the so-called harpooning mechanism, which has long been proposed as a primary process leading to metal atom reactions, the attacking metal atom tosses out its valence electron, hooks the oxidant molecule, and hauls it with the Coulomb force.2–5 By simply calculating the energy difference of the ionization energy (IE) of the metal atom and the electron affinity (EA) of the oxidant molecule, the ET distance can be predicted according to the formula:| RC = ke2/(IE − EA) | (1) |
For over five decades, no experimentally derived impact parameter b, defined as the distance of closest approach for a hypothetical undeflected trajectory of the colliding reagents,1 has been compared quantitatively with RC to provide direct verification of eqn (1) for the harpooning distance. This is primarily a consequence of the difficulty encountered in a scattering experiment to determine the impact parameter b,1 although a few studies have been attempted along this line from the product rotational distributions on the kinematically favored mass combination, e.g. Ba + HI → BaI + H or Rb + HBr → RbBr + H.11–15 “In the absence of any detailed information on the recoil energy of the products”, as pointed out in previous research,13 it was, at best, an upper bound of the maximum impact parameter bmax that could be inferred by assuming the fulfillment of energy conservation. It is significant that in the case that the orbital angular momentum of the products lies in the opposite direction to their rotational angular momentum, considerations of merely rotational state distributions would have led to an overestimation of the total angular momentum of the collisional system, which, in turn, yielded an overestimation of the impact parameter.16 In these cases, it was necessary to acquire the information of the product orbital angular momentum, in conjunction with the rotational state-selective measurements. For the previously well-studied systems such as (Ba + HI) and (Rb + HBr),3–7 there is no experimental EA reported for HI or HBr. In fact, our calculations suggest that their corresponding anions are unstable with negative EA. Hence, one cannot explicitly calculate the electron transfer distance using eqn (1) to make a direct comparison.
Considering that the rotational excitation of the reactants is negligible in the crossed supersonic molecular beams, a very small exit relative translational energy v′r will guarantee l ≈ j′, which corresponds to an extreme case of angular momentum disposal where nearly all of the reactant angular momentum l is channeled into the rotational angular momentum j′ of the product. Here l = μbvr, where μ is the reduced mass of the reactants and vr is the collisional relative velocity. Then b would be derived from the product rotational level j′ at a negligibly small vr′. For the titled reaction Al + O2, the ET distance is calculated from eqn (1) as 2.6 Å using the experimental IE(Al) = 48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 314 cm−1 (or 5.99 eV) and EA(O2) = 3549 cm−1 (or 0.44 eV),17 which can be used for an instructive comparison with the experimentally derived bmax to support the harpooning mechanism. Here, the adiabatic electron affinity is used, as the nuclei can adjust adiabatically with a small distance of about 0.15 Å (the difference between re(O2) and re(O2−)) during the transition from the non-ionic to the ionic state.18
314 cm−1 (or 5.99 eV) and EA(O2) = 3549 cm−1 (or 0.44 eV),17 which can be used for an instructive comparison with the experimentally derived bmax to support the harpooning mechanism. Here, the adiabatic electron affinity is used, as the nuclei can adjust adiabatically with a small distance of about 0.15 Å (the difference between re(O2) and re(O2−)) during the transition from the non-ionic to the ionic state.18
The oxidation dynamics of the Al atom, an important process with potential applications in combustion and rocket propellants, have been studied in the crossed beam experiment by using a laser-induced-fluorescence (LIF) method and recently by the time-sliced ion velocity imaging technique.19–26 The reaction was found to be barrierless with ΔH = −1252 cm−1 (or −3.58 kcal mol−1).23 Due to the small rotational constant of the AlO product (Be = 0.6413 cm−1), almost continuous rotational excitation has been observed.19–26 The speed distributions and angular distributions of the AlO products detected via resonance enhanced multiphoton ionization (REMPI) have been obtained at a collision energy of Ec = 1035 cm−1 (or 2.96 kcal mol−1) by Honma’s group.26 Compared to the study of Honma et al.,26 the improved energy resolution in our crossed beam and time-sliced ion velocity imaging setup27 has, as will be shown below, clearly resolved the two rotational states of the AlO products with a difference of rotational levels of 14 through the P and R branches, respectively, when recorded simultaneously at the same REMPI wavelength. This is necessary for determining the recoil energy distributions and the differential cross sections of the AlO products in a state well-resolved manner. In this work, we present direct evidence of the maximum impact parameter derived from the detailed information on the recoil energy of state-resolved AlO products formed from the titled reaction, Al(2P1/2,3/2) + O2(X3Σ−g) → AlO(X2Σ+) + O(3PJ) at Ec = 507 ± 49 cm−1 (or 1.45 ± 0.14 kcal mol−1), which provides solid evidence in supporting the harpooning mechanism.
Results
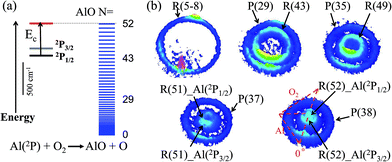
The energetics data of the Al(2P) + O2(X3Σ−g) reaction are shown in Fig. 1(a), and the available energy (Ec − ΔH) for the reaction system is approximately 1760 cm−1. An almost continuous rotational excitation of the AlO products to the energetically available limit is shown in blue in Fig. 1(a). The raw slice images of the AlO(X2Σ+) products at the vibrational ground state v = 0 are exemplified in Fig. 1(b), which were recorded at various wavelengths in the rotational state-selective (1 + 1) REMPI process. The label N in Fig. 1 represents the quantum number of the rotational angular momentum for AlO(X2Σ+) without considering the electronic spin coupling. Importantly, as compared to a previous study,26 this is a well-resolved state result when the two rotational levels of AlO(N and N + 14) are simultaneously probed at the same wavelength via P(N) and R(N + 14) transitions, respectively. The Newton diagram transforms the reactants’ velocity from the lab-frame to the center-of-mass (c.m.) frame. The reaction products will scatter around with a radius centered on the c.m. frame origin. In accordance with the conservation of energy, as N increases up to the highest energetically available level, the velocity mapped ring of the AlO(N) products contracts to a center spot representing an almost zero speed.The speed distributions and angular distributions of the AlO products in different rotational states were extracted from the recorded slice images with the density-to-flux correction.28Fig. 2(a) shows the speed distributions P(v′r) of the AlO(X2Σ+, v = 0, N) products integrated over the whole angular range (0–360°). The speed distribution of AlO(N = 5–8) at low rotational levels shows the peak at ∼500 m s−1, converted to a total kinetic energy release (TKER) of about 1657 cm−1 in the AlO and O co-products. Neglecting a small rotational energy of about 19–46 cm−1 in the AlO products, almost all the available energy (1760 cm−1) of the system is channeled into the translational energy of the products.
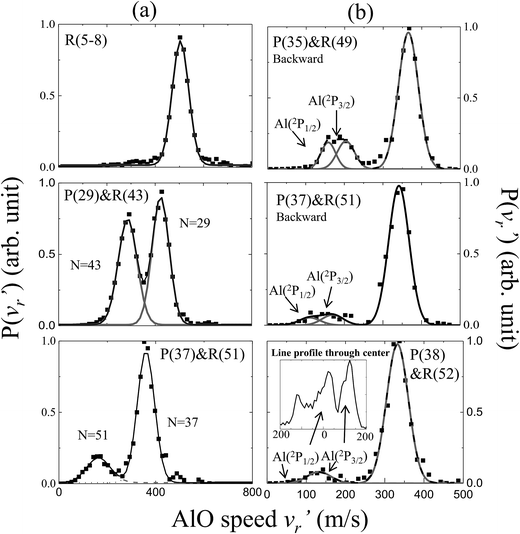 | ||
| Fig. 2 Normalized speed distributions of the AlO(X2Σ+, v = 0, N) products integrated over (a) the whole angular range and (b) the backward scattering direction from the slice images shown in Fig. 1. In accordance with the conservation of energy, the speed of the AlO(N) products in panel (a) decreases as N increases up to the maximum energetically available rotational level. In panel (b), the reactivity of different spin–orbit coupling states for Al(2P) could be resolved in the AlO products at higher rotational levels (N ≥ 49). In the last panel, the generated AlO(N = 52) from Al(2P1/2) and Al(2P3/2) can be clearly discerned from a simple line profile through the center of the raw image in the c.m. frame. | ||
As seen in Fig. 1(b) and 2(a), the P(29) and R(43) branches were recorded simultaneously at 244.543 nm for AlO(v = 0). The outer ring in the slice image with a faster speed of ∼425 m s−1 corresponds to a lower rotational level of N = 29 and the inner ring with a slower speed of ∼290 m s−1 corresponds to a higher rotational level of N = 43. The converted TKERs are 1197 and 557 cm−1 for N = 29 and 43, respectively, with an energy difference of 640 cm−1, which is consistent with the rotational energy space of 649 cm−1 between the two states. According to the conservation of energy, the energy separation between the peaks in the speed distributions should always be consistent with the corresponding internal energy difference of the AlO products between the recorded rotational levels.
As shown in Fig. 1(b) by the velocity mappings and Fig. 2(b) by the speed distributions, our experiments were able to distinguish the AlO products at N = 49, 51 and 52 generated from the oxidations of either Al(2P3/2) or Al(2P1/2), with a small energy difference of ΔE = 112 cm−1 due to spin–orbit coupling. The successful resolving of the spin–orbit reactivity of the Al(2P) atom in the AlO products again demonstrated the high resolution level achieved with our setup.27 As compared to the products at lower N with a larger translational energy, the AlO products at higher N have a greater possibility to resolve the reactivities of Al atoms in different spin–orbit coupling states. This can be easily understood, as a higher energy difference resolution ΔE/ET is related to the products with a smaller translational energy ET. As clearly seen in Fig. 1(b), the signal of the AlO(N = 51 and 52) products in the c.m. frame corresponds to the ground state reaction of Al(2P1/2), while the signal with a larger radius ring corresponds to the excited state reaction of Al(2P3/2). Fig. 2(b) shows the speed distribution of the AlO products integrated over a narrow angular region (160–180°) for better resolution. From the integration of speed distributions in AlO(N = 51) and the population of Al states, we obtained a relative state reactivity of σ(Al(2P1/2))/σ(Al(2P3/2)) = 1.5 ± 0.3, which is half of the ratio obtained at a similar Ecvia LIF.23,24 A direct comparison between the present results and the previous LIF results shall be made with caution. We only observed the difference in the reactivity of two spin–orbit levels of Al (2P1/2 and 2P3/2) at high rotational levels of the AlO products, whereas LIF studies gave the reactivity difference in an all-states-integrated manner.
Notably, the AlO(N = 52) products with v′r ≈ 0 from the oxidation of the ground state Al(2P1/2) become very weak in P(v′r). This is, however, reasonable as P(v′r) is obtained by the integration of the events in the raw images with the (v′r)2 factor taken into account over an angular range in the c.m. polar coordinate. When a line profile is taken through the center of the c.m. frame and roughly along the reactant relative velocity, the AlO(N = 52) products from Al(2P1/2) and Al(2P3/2) are clearly discerned as shown in the last panel in Fig. 2. This simple analysis sensitively sees the AlO product with v′r ≈ 0, which lies at the center point of the c.m. system in the raw image. The above observation actually embodies another advantage of velocity mapping as shown in Fig. 1, where even the products with an almost zero speed distribution can be efficiently recorded.28
Consistent with the energetically available limit as shown in Fig. 1, the highest rotational level that can be observed is Nmax = 52 in the vibrational ground state of the AlO products, which has a rotational energy of about 1751 cm−1. The higher rotational level of the AlO (v = 0, N = 53) product was also detected via the R(53) branch, as shown in Fig. S1.† A zero velocity of the AlO products from the Al(2P3/2) reactants was mapped and no reactive signal was observed for the ground state reaction.
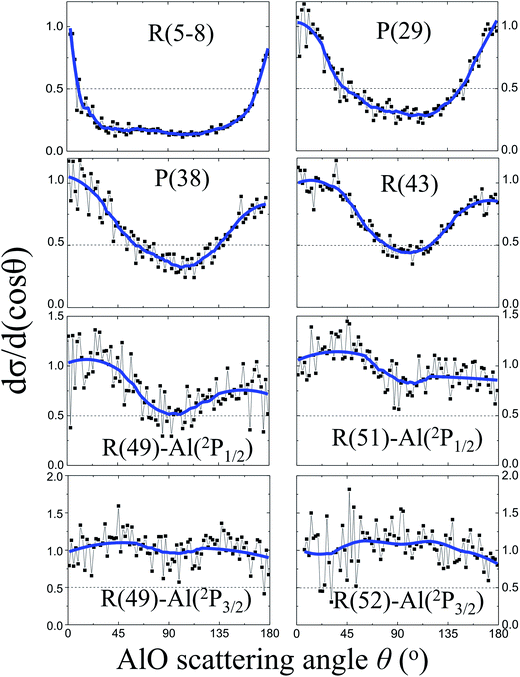
Fig. 3 shows the angular distributions dσ/d(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) of the AlO products at various rotational states. At low rotational levels N = 5–8, the angular distribution of the AlO products is characterized with a sharp backward–forward peak at θ = 180° and 0°, respectively, and is close to the shape of 1/sin
θ) of the AlO products at various rotational states. At low rotational levels N = 5–8, the angular distribution of the AlO products is characterized with a sharp backward–forward peak at θ = 180° and 0°, respectively, and is close to the shape of 1/sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ.16,29 As N increases and approaches the energetically limited value, more products were found to distribute in the sideways direction at θ = 90°. The reactivities of the Al atoms in the 2P1/2 and 2P3/2 states were resolved for the angular distributions of AlO in high rotational levels. Almost isotropic angular distributions were observed for the high rotational level N ≥ 49 from the excited state reaction involving Al(2P3/2) and for N ≥ 51 from the ground state reaction involving Al(2P1/2).
θ.16,29 As N increases and approaches the energetically limited value, more products were found to distribute in the sideways direction at θ = 90°. The reactivities of the Al atoms in the 2P1/2 and 2P3/2 states were resolved for the angular distributions of AlO in high rotational levels. Almost isotropic angular distributions were observed for the high rotational level N ≥ 49 from the excited state reaction involving Al(2P3/2) and for N ≥ 51 from the ground state reaction involving Al(2P1/2).
Discussion
The results based on the present rotational state-selective speed distribution measurements, shown in Fig. 1 and 2, clearly show that the extreme case where the reactant orbital angular momentum was channeled into the product rotational angular momentum, i.e. l ≈ j′, was observed for the title reaction. As a consequence of the conservation of energy and the angular momentum, the almost zero speed of AlO(Nmax = 52) suggests a negligible product orbital angular momentum.The experimental proof for the establishment of the l ≈ j′ condition is of great significance for the direct experimental determination of the largest collision impact parameter bmax. According to the equation 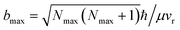 ,30 where ħ is Planck’s constant divided by 2π, bmax is derived to be 2.5 ± 0.2 Å at the relative velocity vr of 910 ± 50 m s−1 in the supersonic crossed beam experiment for the title reaction. It has to be emphasized that the experimentally derived bmax agrees well with the ET distance RC ≈ 2.6 Å from the predicted value based on eqn (1). Thus, the present results provide solid experimental evidence in supporting the harpooning mechanism, i.e. the attacking Al atom uses its valence electron to “harpoon” the oxygen molecule, similar to the reaction mechanism proposed for an alkali atom to react with a halogen molecule.5
,30 where ħ is Planck’s constant divided by 2π, bmax is derived to be 2.5 ± 0.2 Å at the relative velocity vr of 910 ± 50 m s−1 in the supersonic crossed beam experiment for the title reaction. It has to be emphasized that the experimentally derived bmax agrees well with the ET distance RC ≈ 2.6 Å from the predicted value based on eqn (1). Thus, the present results provide solid experimental evidence in supporting the harpooning mechanism, i.e. the attacking Al atom uses its valence electron to “harpoon” the oxygen molecule, similar to the reaction mechanism proposed for an alkali atom to react with a halogen molecule.5
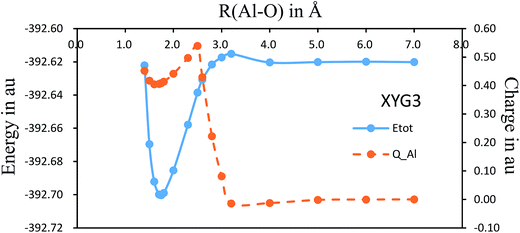
There have been several preliminary theoretical studies for Al–O2.31–33 In particular, Ledentu et al. calculated a potential energy section along the reactant channel studied in the C∞v symmetry with the distance between two oxygen atoms fixed at 1.2171 Å.33 We are constructing the global potential energy surface for the title reaction, where Fig. 4 shows the C∞v potential energy curve with a varying R(Al–O) distance from 7.0 to 1.4 Å while the R(O–O′) distance is being optimized. Along this energy profile, we also show the results from charge analysis. Indeed, a neutral-ionic avoided crossing region exists, around which a sudden electron transfer from Al to O2 occurs. The point with the maximum charge transfer corresponds to R(Al–O) = 2.5 Å, while the co-linear AlOO′ complex has R(Al–O) = 1.735 Å with R(O–O′) = 1.317 Å. Hence, it can be envisioned from Fig. 4 that the electron is first transferred, hooking the ion pairs through the coulombic force, which helps the reaction to proceed further to form an AlOO′ complex before complete dissociation of O–O′. Currently, we are constructing the global potential energy surface for the title reaction to examine the detailed dynamics.
For the barrierless title reaction,21 the opacity function is a step function and the reaction probability is independent of the impact parameter when b ≤ bmax. Thus the reaction cross section σ = πbmax2 is estimated to be 19.6 Å2 at the collision energy of this study. The resultant rate constant k(vr) = vrσ is 1.8 ± 0.02 × (10−10 cm3) per molecule per s with a narrow relative velocity of 910 ± 50 m s−1, which can be compared to the thermal rate constant k(T) = (1.5–1.7) × 10−10 cm3 per molecule per s in the temperature range of T = 300–600 K with a mean relative velocity in the range of 660–930 m s−1.21 The nearly constant value of k(T) in the temperature range is partly caused by a negative dependence of the reaction cross section on the collision energy.21,34 In relation to k(vr), k(T) could be loosely written as k(T) = 〈vrσ(vr)〉T ≈ 〈vr〉〈σ(vr)〉T, where the brackets denote the average over a thermal distribution of the relative velocity at temperature T. Thus, the comparable values of k(vr) and k(T) provide credible evidence for the impact parameter of 2.5 Å obtained here.
The observed negative dependence of the reaction cross section on the collision energy for the title reaction21,34 is understandable. If the reactant passed very quickly, the attractive force, i.e. the coulombic force in the harpooning mechanism, would not be enough to turn the reactant around to let the reaction happen. In other words, with the increase of the collision energy Ec, the centrifugal energy Ecb2/R2 will contribute increasingly as a repulsive energy at the corresponding impact parameter. Thus in order to get an accurate electron transfer distance to compare with the harpooning model, one needs to minimize the dynamics effect of the centrifugal energy and measure the maximum impact parameter at a low collision energy, which leaves enough time for long-range attractive interactions.1 This is indeed the setting of the present experiment.
The experimental observation for the dependence of angular distributions dσ/d(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) on the product rotational angular momentum N can be well interpreted by the model of the angular momentum disposal in a complex-forming reaction as proposed by Kim and Herschbach.16,29 As clearly shown in Fig. 3, the angular distribution displays a trend changing from the backward–forward peaking to an isotropic distribution as the products have been rotationally excited to a high rotational level. At low N, the sharp backward–forward angular distributions suggest that the corresponding plane of collision is conserved with l ≈ l′.16,29 On the other hand, the nearly isotropic distribution at high N implies the effect of nonplanar scattering where a significant angular momentum appears as a product rotation with respect to the random axis with l ≈ j′.16,29
θ) on the product rotational angular momentum N can be well interpreted by the model of the angular momentum disposal in a complex-forming reaction as proposed by Kim and Herschbach.16,29 As clearly shown in Fig. 3, the angular distribution displays a trend changing from the backward–forward peaking to an isotropic distribution as the products have been rotationally excited to a high rotational level. At low N, the sharp backward–forward angular distributions suggest that the corresponding plane of collision is conserved with l ≈ l′.16,29 On the other hand, the nearly isotropic distribution at high N implies the effect of nonplanar scattering where a significant angular momentum appears as a product rotation with respect to the random axis with l ≈ j′.16,29
Experiment–theory comparisons in reaction dynamics always involve averaging over all possible impact parameters. This is true even for a quantity such as the state-resolved differential cross section. In this work, the measurement of the maximum impact parameter will assist and test the quantum chemical calculations to explore the oxidation dynamics of the Al atom in a particular range of impact parameters. Further experimental information regarding the harpooning mechanism can be obtained by studying the stereochemistry of collisions, wherein one can determine the relationship between the non-spherical orbital and the product scattering angle.35–40 A more detailed analysis of differential cross sections from various reactant alignment conditions would offer more clear evidence to establish the reaction mechanism and to allow a 3D visualization of how the chemical transformation takes place.
Methods
The experimental apparatus (Fig. S2†) used in this work has been described elsewhere,28 and the experimental techniques involved the laser-ablation and the crossed-beam setup combined with time-sliced ion velocity imaging detection.27,28,41–44 Only a brief account is provided here. The supersonic aluminum atomic beam (speed ∼ 530 m s−1), produced by laser vaporization of an Al metal rod (97% Al, Alfa) with Ar as the carrier gas, intersected at 90° with the supersonic molecular beam of the pure oxygen molecule (speed ∼ 740 m s−1) in the centre of the ion optics. The Al(2P) atomic beam was characterized by (1 + 1) REMPI via the Al(2D) intermediate state, for Al(2P1/2) at 308.305 nm and Al(2P3/2) 309.360 nm, respectively. With Ar as the carrier gas, we obtained a ratio of Al(2P1/2)/Al(2P3/2) = 0.47 ± 0.03 (one standard deviation per error bar) (Fig. S3†). The AlO products were detected by (1 + 1) REMPI via the D2Σ+ − X2Σ+ transition in the wavelength region of 243–245 nm.26 The probe laser beam was generated from a Continuum Sunlite OPO/OPA laser pumped by a Nd:YAG laser at 355 nm with a 5–9 ns pulse width. A pulse energy of 1–3 mJ was used with a cylindrical lens (f = 500 mm) with the focus direction along the extraction axis. The probe laser had a large spot size of approximately 10 mm in the unfocused direction to cover the molecular-beam-crossed region in the collision plane. The spot size of the probe laser suggests that the time accumulation of the reactive collision events is about 10 μs and this accumulation period narrows the relative velocity to a specified Ec.The product ions with the same velocity were accelerated and projected upwards by the ion optics onto the same point on the position sensitive detector. The detector is composed of two micro-channel plates (75 mm 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 10 μm pores and 12 μm pitch, Photek) and one Phosphor Screen (P43, Photek). Slice images were finally recorded by applying a 30 ns gate pulse onto the detector. To remove the AlO background in the Al atomic beam ablated from the surface of the Al rod due to the oxide contamination, an active subtraction scheme was employed routinely for the images taken with the O2 beam on and off in turn for all data acquisition. In fact, the AlO background in the Al beam has the velocity mapped along the direction of the flying Al beam, and is just outside of the flying area of the reactive products with maximum kinetic energy. Thus the AlO background did not affect the distributions of products in the various rotational levels from which impact parameter information was obtained.
1 10 μm pores and 12 μm pitch, Photek) and one Phosphor Screen (P43, Photek). Slice images were finally recorded by applying a 30 ns gate pulse onto the detector. To remove the AlO background in the Al atomic beam ablated from the surface of the Al rod due to the oxide contamination, an active subtraction scheme was employed routinely for the images taken with the O2 beam on and off in turn for all data acquisition. In fact, the AlO background in the Al beam has the velocity mapped along the direction of the flying Al beam, and is just outside of the flying area of the reactive products with maximum kinetic energy. Thus the AlO background did not affect the distributions of products in the various rotational levels from which impact parameter information was obtained.
The calculations were performed using the XYG3 doubly hybrid density functional.45 With systematic and comprehensive tests, it has been concluded that XYG3 is very accurate for main group chemistry.46 Recently we have shown that XYG3 can describe the simplest tri-atomic chemical reaction, H + HH′ → H′ + H2, in a state-to-state level well,47 and can provide accurate potential energy surfaces for a series of hydrogen abstraction reactions48 for quantum dynamics applications. The basis set used is 6-311+G(3df,2p).
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are very grateful to Prof. Kopin Liu (IAMS, Taipei) for many stimulating discussions. This work was supported by the National Natural Science Foundation of China (No. 21322309, No. 21327901, No. 21673047 and No. 21688102) and the Program for Professor of Special Appointment (Eastern Scholar) at Shanghai Institutions of Higher Learning.References
-
R. D. Levine, Molecular Reaction Dynamics, Cambridge University Press, Cambridge, 2005 Search PubMed
.
- J. L. Magee, J. Chem. Phys., 1940, 8, 687 CrossRef CAS
.
- J. C. Polanyi, Appl. Opt., 1965, 4, 109–127 CrossRef
.
- D. R. Herschbach, Appl. Opt., 1965, 4, 128–144 CrossRef
.
- D. R. Herschbach, Adv. Chem. Phys., 1966, 10, 319–393 CrossRef
.
-
M. Polanyi, Atomic reactions, Williams & Norgate, Ltd., London, 1932 Search PubMed
.
- W. Heller, Trans. Faraday Soc., 1937, 33, 1556–1570 RSC
.
- C. E. H. Bawn, W. F. Berg, G. Gee and H. W. Melville, Annu. Rep. Prog. Chem., 1942, 39, 7–69 RSC
.
- S. A. Edelstein and P. Davidovits, J. Chem. Phys., 1971, 55, 5164–5170 CrossRef CAS
.
- J. H. Birely, R. R. Herm, K. R. Wilson and D. R. Herschbach, J. Chem. Phys., 1967, 47, 993 CrossRef CAS
.
- C. Noda, J. S. Mckillop, M. A. Johnson, J. R. Waldeck and R. N. Zare, J. Chem. Phys., 1986, 85, 856–864 CrossRef CAS
.
- J. E. Mosch, S. A. Safron and J. P. Toennies, Chem. Phys. Lett., 1974, 29, 7–12 CrossRef CAS
.
- P. H. Vaccaro, A. A. Tsekouras, D. Zhao, C. A. Leach and R. N. Zare, J. Chem. Phys., 1992, 96, 2786–2798 CrossRef CAS
.
- A. A. Tsekouras, C. A. Leach, K. S. Kalogerakis and R. N. Zare, J. Chem. Phys., 1992, 97, 7220–7225 CrossRef CAS
.
- K. S. Kalogerakis and R. N. Zare, J. Chem. Phys., 1996, 104, 7947–7964 CrossRef CAS
.
- S. K. Kim and D. R. Herschbach, Faraday Discuss., 1987, 84, 159–169 RSC
.
-
S. G. Lias, J. E. Bartmess, J. F. Liebman, J. L. Holmes, R. D. Levin and W.G. Mallard, Ion energetics data, in Nist chemistry webbook, NIST standard reference database Number 69, ed. P. J. Linstrom and W. G. Mallard, NIST, Gaithersburg MD, 2017, p. 20899, DOI:10.18434/T4D303.
.
- K. M. Ervin, I. Anusiewicz, P. Skurski, J. Simons and W. C. Lineberger, J. Phys. Chem. A, 2003, 107, 8521–8529 CrossRef CAS
.
- P. J. Dagdigian, H. W. Cruse and R. N. Zare, J. Chem. Phys., 1975, 62, 1824–1833 CrossRef CAS
.
- M. Costes, C. Naulin, G. Dorthe, C. Vaucamps and G. Nouchi, Faraday Discuss., 1987, 84, 75–86 RSC
.
- C. Naulin and M. Costes, J. Phys. Chem., 1994, 98, 5593–5596 CrossRef CAS
.
- K. M. Chen, C. H. Sung, J. L. Chang, T. H. Chung and K. H. Lee, Chem. Phys. Lett., 1995, 240, 17–24 CrossRef CAS
.
- C. Naulin and M. Costes, Chem. Phys. Lett., 1999, 310, 231–239 CrossRef CAS
.
- K. Honma, J. Chem. Phys., 2003, 119, 3641–3649 CrossRef CAS
.
- M. Ishida, T. Higashiyama, Y. Matsumoto and K. Honma, J. Chem. Phys., 2005, 122, 204312 CrossRef PubMed
.
- K. Honma, K. Miyashita and Y. Matsumoto, J. Chem. Phys., 2014, 140, 214304 CrossRef PubMed
.
- C. W. Dong, J. X. Liu, F. F. Li and F. Y. Wang, Chin. J. Chem. Phys., 2016, 29, 99–104 CrossRef CAS
.
- J. J. Lin, J. G. Zhou, W. C. Shiu and K. P. Liu, Rev. Sci. Instrum., 2003, 74, 2495–2500 CrossRef CAS
.
- W. B. Miller, S. A. Safron and D. R. Herschbach, Discuss. Faraday Soc., 1967, 44, 108–122 RSC
.
- T. Gonzalez-Lezana, O. Roncero, P. Honvault, J. M. Launay, N. Bulut, F. J. Aoiz and L. Banares, J. Chem. Phys., 2006, 125, 094314 CrossRef PubMed
.
- D. Reignier, T. Stoecklin, S. D. Le Picard, A. Canosa and B. R. Rowe, J. Chem. Soc., Faraday Trans., 1998, 94, 1681–1686 RSC
.
- M. V. Pak and M. S. Gordon, J. Chem. Phys., 2003, 118, 4471 CrossRef CAS
.
- V. Ledentu, A. Rahmouni, G.-H. Jeung and Y. S. Lee, Bull. Korean Chem. Soc., 2004, 25, 1645–1647 CrossRef CAS
.
-
N. L. Garland, Gas-phase metal reactions, North-Holland, Amsterdam, 1992 Search PubMed
.
- J. M. Mestdagh, B. Soep, M. A. Gaveau and J. P. Visticot, Int. Rev. Phys. Chem., 2003, 22, 285–339 CrossRef CAS
.
- F. Wang, J. S. Lin and K. Liu, Science, 2011, 331, 900–903 CrossRef CAS PubMed
.
- F. Y. Wang, K. P. Liu and T. P. Rakitzis, Nat. Chem., 2012, 4, 636–641 CrossRef CAS PubMed
.
- F. Wang, J.-S. Lin and K. Liu, J. Chem. Phys., 2014, 140, 084202 CrossRef PubMed
.
- F. J. Aoiz, M. Brouard, S. D. Gordon, B. Nichols, S. Stolte and V. Walpole, Phys. Chem. Chem. Phys., 2015, 17, 30210–30228 RSC
.
- K. Liu, Annu. Rev. Phys. Chem., 2016, 67, 91–111 CrossRef CAS PubMed
.
- M. A. Duncan, Rev. Sci. Instrum., 2012, 83, 041101 CrossRef PubMed
.
- K. P. Liu, Annu. Rev. Phys. Chem., 2001, 52, 139–164 CrossRef CAS PubMed
.
- A. T. J. B. Eppink and D. H. Parker, Rev. Sci. Instrum., 1997, 68, 3477–3484 CrossRef CAS
.
- C. R. Gebhardt, T. P. Rakitzis, P. C. Samartzis, V. Ladopoulos and T. N. Kitsopoulos, Rev. Sci. Instrum., 2001, 72, 3848–3853 CrossRef CAS
.
- Y. Zhang, X. Xu and W. A. Goddard III, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 4963–4968 CrossRef CAS PubMed
.
- N. Q. Su and X. Xu, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 721–747 CrossRef CAS
.
- N. Q. Su, J. Chen, Z. Sun, D. H. Zhang and X. Xu, J. Chem. Phys., 2015, 142, 021104 Search PubMed
.
- J. Chen, N. Q. Su, Z. Sun, X. Xu and D. H. Zhang, J. Comput. Chem., 2017, 38, 2326–2334 CrossRef CAS PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7sc03314a |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2018 |