Open Access Article
Open Access ArticleTracking the picosecond deactivation dynamics of a photoexcited iron carbene complex by time-resolved X-ray scattering†
Denis
Leshchev
 *a,
Tobias C. B.
Harlang
bc,
Lisa A.
Fredin
*a,
Tobias C. B.
Harlang
bc,
Lisa A.
Fredin
 d,
Dmitry
Khakhulin
e,
Yizhu
Liu
f,
Elisa
Biasin
c,
Mads G.
Laursen
c,
Gemma E.
Newby
a,
Kristoffer
Haldrup
c,
Martin M.
Nielsen
d,
Dmitry
Khakhulin
e,
Yizhu
Liu
f,
Elisa
Biasin
c,
Mads G.
Laursen
c,
Gemma E.
Newby
a,
Kristoffer
Haldrup
c,
Martin M.
Nielsen
 c,
Kenneth
Wärnmark
f,
Villy
Sundström
b,
Petter
Persson
c,
Kenneth
Wärnmark
f,
Villy
Sundström
b,
Petter
Persson
 d,
Kasper S.
Kjær
bc and
Michael
Wulff
*a
d,
Kasper S.
Kjær
bc and
Michael
Wulff
*a
aEuropean Synchrotron Radiation Facility, 71 Avenue des Martyrs, 38000 Grenoble, France. E-mail: leshchev.denis@gmail.com
bDepartment of Chemical Physics, Lund University, P. O. Box 12 4, 22100 Lund, Sweden
cMolecular Movies Group, Department of Physics, Technical University of Denmark, Lyngby, DK-2800, Denmark
dTheoretical Chemistry Division, Lund University, P. O. Box 124, 22100 Lund, Sweden
eEuropean XFEL GmbH, Holzkoppel 4, 22869 Schenefeld, Germany
fCentre for Analysis and Synthesis, Department of Chemistry, Lund University, P. O. Box 12 4, Lund 22100, Sweden
First published on 31st October 2017
Abstract
Recent years have seen the development of new iron-centered N-heterocyclic carbene (NHC) complexes for solar energy applications. Compared to typical ligand systems, the NHC ligands provide Fe complexes with longer-lived metal-to-ligand charge transfer (MLCT) states. This increased lifetime is ascribed to strong ligand field splitting provided by the NHC ligands that raises the energy levels of the metal centered (MC) states and therefore reduces the deactivation efficiency of MLCT states. Among currently known NHC systems, [Fe(btbip)2]2+ (btbip = 2,6-bis(3-tert-butyl-imidazol-1-ylidene)pyridine) is a unique complex as it exhibits a short-lived MC state with a lifetime on the scale of a few hundreds of picoseconds. Hence, this complex allows for a detailed investigation, using 100 ps X-ray pulses from a synchrotron, of strong ligand field effects on the intermediate MC state in an NHC complex. Here, we use time-resolved wide angle X-ray scattering (TRWAXS) aided by density functional theory (DFT) to investigate the molecular structure, energetics and lifetime of the high-energy MC state in the Fe–NHC complex [Fe(btbip)2]2+ after excitation to the MLCT manifold. We identify it as a 260 ps metal-centered quintet (5MC) state, and we refine the molecular structure of the excited-state complex verifying the DFT results. Using information about the hydrodynamic state of the solvent, we also determine, for the first time, the energy of the 5MC state as 0.75 ± 0.15 eV. Our results demonstrate that due to the increased ligand field strength caused by NHC ligands, upon transition from the ground state to the 5MC state, the metal to ligand bonds extend by unusually large values: by 0.29 Å in the axial and 0.21 Å in the equatorial direction. These results imply that the transition in the photochemical properties from typical Fe complexes to novel NHC compounds is manifested not only in the destabilization of the MC states, but also in structural distortion of these states.
Introduction
The development of iron-based photofunctional complexes can provide a cost effective and environmentally benign path towards large-scale solar energy applications. A central challenge in developing light harvesting complexes with 3d transition metals is their weak ligand field splitting (LFS) compared to their 4d or 5d counterparts. Due to the weak LFS of 3d transition metal complexes, their photoactive metal-to-ligand charge-transfer (MLCT) excited states are efficiently deactivated by lower energy metal-centered high-spin (MC) states. For example, the MLCT states of a prototypical FeII polypyridyl complex relax to a quintet metal centered (5MC) state on the hundred femtosecond time scale,1–13 whereas the MLCT lifetime of their RuII polypyridyl analogs are measured in hundreds of nanoseconds.14 Efforts in understanding and controlling the photocycle of FeII complexes have spurred intensive studies of ultrafast MLCT → 5MC deactivation, known as light induced spin crossover (SCO).1–13,15 Additionally, the SCO phenomenon could potentially be used in novel memory devices,16–21 which have prompted studies of the properties of the 5MC state and recovery to the singlet ground state (GS).22–40 In spite of the inherent challenges in utilizing Fe photosensitizers, recent developments of Fe complexes based on N-heterocyclic carbene41 (NHC) and CN− ligands42 have provided MLCT lifetimes on the order of tens of picoseconds. These systems have been developed towards efficient electron injection into TiO2 electrodes,43 and they have been extended towards photoluminescence in the FeIII oxidation state.44 Density functional theory (DFT) calculations have shown that the improved performance of the Fe–NHC systems is due to increased electron density on the metal provided by strong σ-donating NHC ligands which effectively destabilize the unwanted MC states.45,46 This results in inhibiting the MLCT deactivation and bypassing the 5MC state in the excite state cascade similarly to chemically akin RuII based sensitizers.45,46 A different chemical approach was recently introduced with highly strained halogenated polypyridyls which utilize the quintet GS.47,48 Here, the structural restrictions from the halogen atoms placed on the ligand side groups increase the energy of the 3MC state, as well as the crossing barrier between the MLCT and 3MC states, which results in MLCT lifetimes as long as 17.4 ps.48 The rich photophysics of all these novel systems, compared to the traditional polypyridyl-based FeII SCO complexes, calls for a better understanding how different electronic and structural factors affect the MLCT deactivation cascade. Specifically, a thorough examination of the excited state potential surfaces, i.e. characterization of molecular geometries and energies in the various states with both theory and experiments, will help to find the connection between structure and function in these systems. Such mechanistic understanding of their photocycles will help to develop improved synthetic rules for making better photosensitizers for light harvesting applications.In this work we investigate the structural dynamics of the Fe–NHC complex [Fe(btbip)2]2+ (btbip = 2,6-bis(3-tert-butyl-imidazol-1-ylidene)pyridine) (Fig. 1) in acetonitrile (MeCN) solution following photo-excitation to the MLCT manifold, in order to examine the impact of the strong NHC ligand field on the excited state structure, energy and relaxation kinetics. The transient optical absorption spectroscopy experiments previously conducted on this complex,49 indicated that upon excitation to the MLCT manifold, the system decays into a vibrationally hot MC state in 300 fs. A 31 ps component was tentatively assigned to vibrational cooling of this MC state. Complete recovery of the GS spectrum was observed in 230 ps and assigned to GS recovery from the MC state. Since the same compound with methyl (Me) side groups returned to the ground state much faster (∼10 ps),49 the origin of the 230 ps-lived MC state in [Fe(btbip)2]2+ was ascribed to the presence of the bulky tBu side groups that diminish the LFS of the NHC ligands through steric repulsion. The nature of the excited MC state was initially assigned as a 5MC state by simple analogy with typical FeII SCO complexes characterized by weak LFS. Ultrafast MLCT deactivation towards a 5MC state has also been discussed for [Fe(btbip)2]2+ based on recent advanced quantum dynamics simulations.50 The focus of the work, however, was mainly on the early few-ps dynamics of the relaxation from the initially populated 1MLCT state rather than on the relaxed intermediate structure associated with the ∼230 ps excited state lifetime.50 On the other hand, the assignment of the intermediate MC state in [Fe(btbip)2]2+ as 5MC is in stark contrast with other Fe NHC complexes. For all other Fe NHC complexes, it has been argued that the NHC σ-donation is sufficiently strong to alter the MLCT deactivation pathway to proceed via an intermediate 3MC state, bypassing the 5MC state altogether.41,51–53 Further questions regarding the quintet assignment of the MC state of [Fe(btbip)2]2+ can be raised based on the recent spectroscopic works on FeII complexes with expanded cage and push–pull ligands.54,55 There, the few-100's ps lifetime of an MC state was suggested to be indicative of its 3MC character.54,55 In line with this suggestion, a 450 ps lived 3MC state was recently reported for sterically strained RuII complex with weak LFS.56–58 Thus, the 230 ps-lived intermediate MC state of [Fe(btbip)2]2+ provides a non-trivial case to investigate the competition between strong σ-donation from NHC ligands and steric repulsion caused by tBu groups. On the one hand, [Fe(btbip)2]2+ is fundamentally different from traditional photosensitizer complexes with long MLCT lifetimes followed by deactivation via short-lived 3MC scavenger states, to which several of the new Fe NHC complexes seem to belong. On the other hand, [Fe(btbip)2]2+ substantially differs from weak LFS FeII SCO complexes that deactivate to metastable 5MC states, often with ns or longer lifetimes. Therefore, determining the spin, structure and energy of the intermediate MC state in [Fe(btbip)2]2+ will provides new insight in the deactivation cascade of novel FeII complexes.
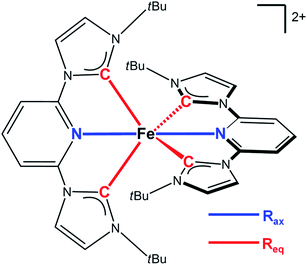 | ||
| Fig. 1 Structure of the [Fe(btbip)2]2+ complex studied in this work. The key structural parameters defining the structure of the molecule are highlighted with colors. | ||
Recent progress in time-resolved X-ray methods provides timely opportunities to characterize the photophysics of [Fe(btbip)2]2+ in greater detail.25,59–63 In this work we employ time-resolved wide angle X-ray scattering (TRWAXS) – an established technique which probes the structural changes in the solute with sub-Å precision,25,59 making it suitable for monitoring the character and structure of the excited MC state in [Fe(btbip)2]2+. Since the lifetime of the intermediate MC state in [Fe(btbip)2]2+ is on the order of hundreds of picoseconds, the properties of this state can be firmly characterized by a synchrotron-based time-resolved experiment taking advantage of the high stability and energy tunability of the X-ray source. The latter provides an opportunity of using high energy X-rays allowing the measurement of scattering patterns up to high scattering vectors q ≳ 10 Å−1, a great advantage for the refinement of the excited state structures. TRWAXS is also highly sensitive to the time dependent thermodynamic response of the solvent,59 which, as we demonstrate in this work, can be used to determine the energy of the excited states. In parallel with the TRWAXS measurements, we perform extensive DFT calculations to support the experimental findings regarding the structure and energy. By comparing the DFT results obtained using different functionals with the experimental data, we identify the ones providing the best agreement with the data in order to improve future theoretical predictions. This detailed combination of computational and experimental characterization deepens our understanding of the NHC family of compounds.
Experimental
The TRWAXS measurements were performed on beamline ID09 at the European Synchrotron Radiation Facility (ESRF, Grenoble). The experimental setup is described in the literature,64 whereas the specific details of the present study are summarized in the ESI.† All scattering patterns were measured with the FReLoN area detector,65 azimuthally integrated and reduced to difference scattering curves ΔS(q,t) (with t being the time delay between the laser and X-ray pulses, q = (4π/λ)sin(2θ/2) with λ and 2θ being the X-ray wavelength and the scattering angle respectively) according to standard procedures.66,67 To follow the structural dynamics of [Fe(btbip)2]2+ in a 9 mM MeCN solution, the data was collected in two separate runs using different X-ray energies, 25.2 keV and 18 keV. By using a multilayer monochromator, the X-ray energy bandwidth of the undulator harmonics were reduced to 1.55% and 1.9% for the 25.2 keV and 18 keV runs respectively, which greatly enhances the structural sensitivity compared to the conventional raw undulator pink beam measurements while maintaining high X-ray flux.67 Note that using high energy X-rays gives access to a wider range of scattering vectors q, allowing for a more precise structural analysis.68 The higher X-ray flux and detector efficiency at 18 keV made the 18 keV measurements four times faster per time delay than at 25.2 keV. The 18 keV dataset was therefore acquired with more laser/X-ray time delays to better resolve the excited state kinetics of the molecule. By contrast, the 25.2 keV run was done with only one time delay, 150 ps, in order to obtain the best possible structural refinement of the MC state.The interpretation of the TRWAXS data was conducted according to the established framework,69 where the experimental curves are fitted with theoretical signals from three contributions: the changes in the solute structure, solvation shell rearrangements (also referred to as the cage term) and the changes in the bulk solvent structure as a result of (adiabatic) heating. We note that the inclusion of the density change component in the solvent response did not improve the fits in the time range 0–400 ps (see ESI†) unlike in recent work on aqueous solutions of similar FeII complexes.29,70 The analysis is based on structural models of the complex and the surrounding solvation shell (cage term) which were calculated by DFT and classical molecular dynamics (MD) simulations, respectively. The difference signal for the bulk solvent temperature increase was measured according to the standard procedure using azobenzene molecules.71 The details of the analysis and the theoretical calculations are described in the ESI.†
Results and discussion
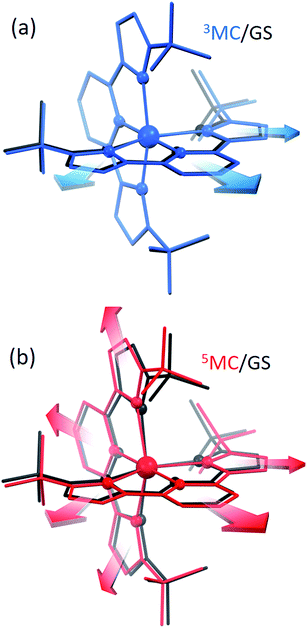
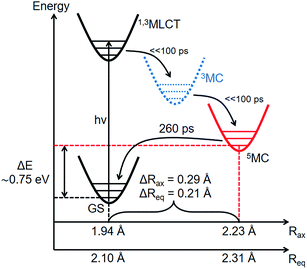
Since the MLCT state of [Fe(btbip)2]2+ has been shown to decay on the 300 fs time scale, the relevant states for 100 ps time-resolved experiments are the GS, 3MC, and 5MC states. The structure of these states were fully relaxed with no symmetry constraints, allowing for all possible Jahn–Teller effects, using the PBE0 (ref. 72–74) functional and a triple-ζ basis set75–77 which is known to give good structural results for Fe–NHC complexes.45,46 A continuum model78 for the MeCN solvent was used to simulate the solvent conditions and to provide charge screening for the metal complexes. The changes in the structure of the complex in the 3MC and the 5MC states compared to the GS are shown in Fig. 2. The structure of [Fe(btbip)2]2+ in the three states is parameterized by two bond lengths,79 namely the axial Fe–NPy (Rax) and equatorial Fe–CNHC (Req) bond lengths (Fig. 1). Their values are summarized in Table 1. The calculated GS (t2g)6 (for convenience we use the notation for the Oh symmetry) structure of [Fe(btbip)2]2+ is in good agreement with X-ray crystallographic data49 and is characterized by a distorted octahedral configuration around the FeII center, with Rax (1.935 Å) being shorter than Req (2.10 Å). The calculated 3MC (t2g)5(eg)1 state has one ligand further away than the other, as only one antibonding eg orbital is populated (further discussions in ESI†). Specifically, the Req and Rax bond of the first ligand are elongated by ∼0.2 Å, whereas Rax of the second ligand is elongated by ∼0.1 Å. In the 5MC (t2g)4(eg)2 state, where two antibonding orbitals are occupied, both ligands are repelled equally from the Fe center by ∼0.3 Å and ∼0.2 Å for Rax and Req, respectively.| GS (1MC) | 3MC | 5MC | |||
|---|---|---|---|---|---|
| Calc. | Exp.c | Calc. | Calc. | Exp. | |
| a Calculated using B3LYP*/6-311G(d,p)/PCM(MeCN). b Calculated using PBE0/6-311G(d,p)/PCM(MeCN). The standard deviation of the calculated bond lengths was found to be 0.001 Å. c From crystallographic data in ref. 49. d Marks I and II correspond to the ligand numbering. | |||||
| E (eV)a | 0 | 0 | 0.95 | 0.72 | 0.75 ± 0.15 |
| R ax (Å)b, (Fe–NPy) | 1.94 | 1.939 | 2.04 (I)d | 2.23 | 2.23 ± 0.03 |
| 2.17 (II)d | |||||
| R eq (Å)b, (Fe–CNHC) | 2.10 | 2.096 | 2.13 (I)d | 2.32 | 2.31 ± 0.02 |
| 2.29 (II)d | |||||
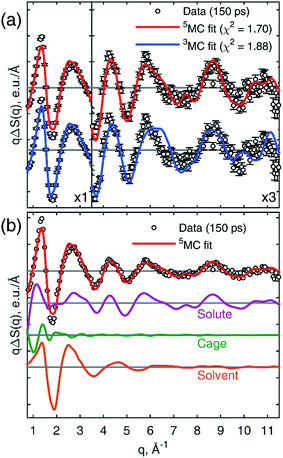
Fig. 3a shows a comparison of the calculated 3MC and 5MC signals fitted to the 25.2 keV data recorded 150 ps after laser excitation. The 5MC signal gives the best fit with a χ2 value of 1.70 compared with 1.88 for 3MC in agreement with previous assignments.49,50Fig. 3b shows the components used for fitting the data. The minor discrepancy between the data and the fit in the range 1.5–2.0 Å−1 might be due to the simplified description of the cage term in the classical MD simulation. The cage term was simulated with a purely classical MD, which accounts for solvation effects arising from the structural changes in the molecule, but it neglects the electronic charge redistribution in the molecule from the GS to 5MC. This effect is included in ab initio MD simulations and, as was shown for aqueous [Fe(bpy)3]2+,80 gives a more significant reorganization of the solvation shell. Constraining the fit to the high-q range of the data (q > 2.5 Å−1), where the cage term is insignificant, increases the contrast between the 3MC and 5MC states from a statistical point of view giving χ2 values of 1.03 and 1.56 for 5MC and 3MC, respectively. This further supports the excited state assignment as 5MC (see ESI†).
The structural refinement of the excited states of [Fe(btbip)2]2+ is non-trivial due to its many degrees of freedom and the (near) similar scattering power of the Fe/C and Fe/N atom pairs that dominate the signal in the high-q range. An individual refinement of all pairs of interatomic distances would significantly exceed the maximal number of parameters that can reliably be inferred from the TRWAXS signal.67,68 Thus, we have developed a model where the key interatomic distances are used to define the structure of the rest of the molecule. By varying these parameters and from those determine the resulting changes to the rest of the structure, one can refine the overall molecular structure within the framework of the proposed structural model. The key is that the parameters chosen need to define the relevant reaction coordinates associated with the structural dynamics.
Previous work on FeII SCO complexes have established that the structural changes induced by the transition from the GS to 5MC are well described by parameterizing the global structure through parameters that define the shape of the first Fe coordination shell, including metal–ligand bond lengths, ligand bite angles and ligand rocking angles, as the reaction coordinates.22–40,81–86 For example, the structural dynamics from the spin transitions in [Fe(terpy)2]2+ – which is structurally similar to [Fe(btbip)2]2+ – were successfully described by including only the axial bond length and the bending angle of the ligand as reaction coordinates.26–29 In recent TRWAXS measurements on [Co(terpy)2]2+, the excited state refinement was done using the axial bond length as the fitting parameter while maintaining the ratio between the axial and equatorial bond length constant.79 Since there is redundancy in any chosen set of coordinates, as they are interrelated (e.g. changing bond angles often results in changes to metal–ligand bond lengths), we have chosen the fewest coordinates possible that describe the fully relaxed minima to avoid overfitting. In the case of [Fe(btbip)2]2+ we choose the axial bond length Rax and the equatorial one Req – which combined define the bending angle of the ligand – as the two independent reaction coordinates. This choice is based on the sensitivity of TRWAXS: the largest contribution to the high-q signal is from the Fe–NPy and Fe–CNHC pairs which makes them the natural parameters in the fitting procedure. To map the overall atomic positions characterized by the selected structural parameters, we have implemented a procedure based on the interpolation between the structures produced by varying the values of Rax and Req and performing constrained DFT for each (Rax, Req) point. Details of the DFT calculations and the associated structural fitting procedure are summarized in the ESI.†
The refined structure of [Fe(btbip)2]2+ in the 5MC state is obtained by fitting the data in the high-q range (q ≥ 2.5 Å−1) according to the model described above, with the DFT-optimized 5MC state (Rax = 2.231 Å, Req = 2.317 Å) as a starting geometry. The result of the refinement is: Rax = 2.23 ± 0.03 Å and Req = 2.31 ± 0.02 Å (Table 1). The good agreement between the theoretically optimized 5MC structure and the experimentally fitted structure validates the DFT method (PBE0/6-311G(d,p)/PCM(MeCN)) to predict excited state structures in (quasi) equilibrium. Note that our refinement procedure allows for an experimental determination of the global molecular structure as a function of two bond distances rather than the refinement of these two distances alone. Moreover, the method employed here can be used for the refinement of many organometallic complexes which do not contain pairs of heavy atoms. While the latter has been traditionally seen as a necessary condition for the structural refinement using TRWAXS,87–95 the present work, together with the recent experiments on [Co(terpy)2]2+,79 extend the applicability of the TRWAXS technique significantly.
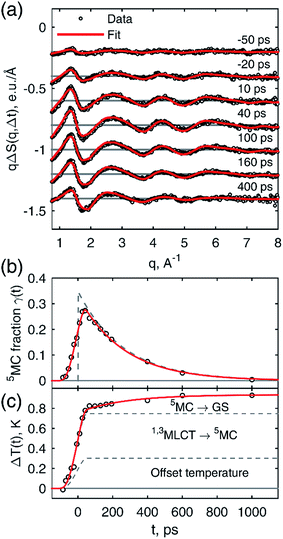
The many time points in the 18 keV dataset were used to analyze the excited state kinetics of [Fe(btbip)2]2+. Here we used the global fit approach,66,69 which ties the reaction kinetics to the hydrodynamic state of the liquid via the conservation of mass and energy (see ESI† for details). Fig. 4a shows a comparison of the fitted theoretical and experimental ΔS(q,t) curves for a subset of time points. For all time points we find a very good agreement between the experimental data and the model fit. This is also the case when comparing the global fit of the excited state fraction γ(t) and the solvent temperature ΔT(t) to the values obtained from fits of the individual time points (Fig. 4b and c). From the global fitting we find that immediately (≪100 ps) after the excitation event, 35 ± 1% of the [Fe(btbip)2]2+ molecules in the probed sample volume arrive in the 5MC state within the 100 ps time resolution of the experiment. This is followed by the decay of the 5MC to the GS with a time constant of 260 ± 10 ps, in fair agreement with the 230 ps lifetime obtained from optical spectroscopy.49 The temperature increase of the bulk solvent is tied to the solute excited state population dynamics, with a prompt increase followed by further growth on the 260 ps time scale. The sharp temperature rise appears around time zero and is partly due to fast relaxation from the MLCT to 5MC (perhaps through a short lived 3MC intermediate50) and the associated redistribution of most of the photon energy into the solvent. A fraction of the initial solvent temperature increase could not be attributed to the relaxation of the excited molecules as discussed further below. After 100 ps the temperature grows due to the release of the 5MC state energy following its decay to the GS. The three contributions to the temperature dynamics are shown in Fig. 4c.
After thermal relaxation of the excited species we observe a temperature rise of 0.94 K. Considering the initial excitation fraction, 35%, and the amount of energy dissipated into the solvent from photon absorption, we expect a 0.64 K temperature rise. The difference, 0.3 K, comes from an unknown source. Considering the relatively low laser fluence (0.052 J cm−2) and the relatively long laser pulse, 1.2 ps (FWHM), we can exclude multi-photon excitation of the solvent as the additional heat source. To verify this, we performed TRWAXS measurements on neat MeCN under similar experimental conditions and did not observe any detectable signal. The 0.3 K temperature rise might point towards an ultrafast deactivation (≪100 ps) of the MLCT state to the GS, for example via an intermediate MC-like state such as 3MC. We estimate that an additional 17 ± 1% of excited solute molecules could relax in this way, corresponding to a total excited state fraction of 52 ± 1%. We note that the excited state fraction and temperature rise are in fair agreement with the expected values of 58% and 1.06 K, respectively, calculated using the laser fluence, X-ray beam size and optical density (see ESI† for more details). Understanding the nature of the observed temperature offset requires better time resolution which is beyond the scope of the present study.
Based on the simple kinetics and the clear observation of the temperature rise from the decay of the 5MC, the energy difference between the 5MC and GS states ΔE can be determined. Although the 5MC → GS relaxation and the corresponding temperature rise were discussed in the TRWAXS work on [Fe(bpy)3]2+,70,96 this work represents the first determination of the complex's energy in the vibrationally relaxed 5MC state, to the best of our knowledge. After incorporation of the energy difference into the global fitting procedure, we arrive at a value of ΔE = 0.75 ± 0.15 eV (see ESI† for details). While DFT is known to give robust structural information for organometallic complexes, irrespective of the functional choice, the sensitivity of the calculated 5MC energy on the choice of the functional has previously been seen for other Fe high spin/low spin complexes. In particular, the amount of the Hartree–Fock exchange used in hybrid functionals can significantly impact the calculated energy of the same geometry.97,98 Thus, we compared PBE0,72–74 PBE0-D3,99 B3LYP,100 B3LYP*,101,102 CAMB3LYP,103 and TPSS104–106 calculated energies with the experimental information about the 5MC state energy. The calculated energy of the 5MC state was found to depend significantly on the choice of functional, with the B3LYP* energy of 0.72 eV in significantly better agreement with the experimental result compared to the PBE0 energy of 0.14 eV. At the same time, DFT optimizations using these two functionals were found to give very similar geometries for the structure of the 5MC state, that are also in good agreement with the experiments (further details in ESI†). It is interesting to note that in terms of energy levels, B3LYP* gives the best agreement with the experiment among the functionals tested here for this short-lived intermediate, similar to what was previously observed in other FeII high and low spin complexes.97 While the present results for [Fe(btbip)2]2+ are limited in scope, they point to encouraging prospects to use a combination of TRWAXS and DFT to provide a reliable understanding of the potential energy landscape in these kinds of photosensitizers that have otherwise often been difficult to characterize.
Combining the structural and energetic data obtained here, the complete photocycle of [Fe(btbip)2]2+, from the initial photoexcitation to ground state recombination, is presented in Fig. 5. The experimentally determined values for the bond lengths and the energy levels are summarized in Table 1. As was initially suggested by optical spectroscopy,49 the excited state behavior of [Fe(btbip)2]2+ is similar to that of other FeII polypyridine complexes: upon excitation to MLCT, the complex quickly undergoes intersystem crossing and ultimately ends up in a longer lived 5MC state. In spite of the short MC state lifetime of <300 ps, we find that the LFS of [Fe(btbip)2]2+ is not strong enough to alter the MLCT deactivation pathway such that it would proceed to the GS by only populating the 3MC intermediate. This finding indicates that, at least for NHC systems, the short MC state lifetime is not indicative of its 3MC character, as suggested for expanded cage and push–pull compounds in recent spectroscopic works54,55 and observed in weak LFS RuII based compounds.56–58 However, the structural rearrangements upon relaxation to the 5MC state have unusually large amplitudes as compared to similar FeII complexes. For [Fe(bpy)3]2+ and [Fe(terpy)2]2+, the Fe–N bonds expand isotropically by 0.22 Å,27,28 but in the case of [Fe(btbip)2]2+, the axial Rax and equatorial Req bonds expand by 0.29 Å and 0.21 Å, respectively. Recent computational results on complexes with NHC and CN− ligands suggest that the increase in the ligand field results in pushing the excited state minima away from the GS minima along the metal-to-ligand bond length reaction coordinate.42,45,46 The structure of [Fe(btbip)2]2+ in its 5MC state observed here confirms this trend and illustrates the effect of the σ-donating carbene ligands on the excited states structure of the complex. Interestingly, for the sister compound [Fe(bmip)2]2+, which suffers less from steric hindrance than [Fe(btbip)2]2+ due to its smaller Me side groups, calculations suggest even larger extensions of the 5MC state, 0.34 Å and 0.25 Å for ΔRax and ΔReq, respectively.45 Since the predicted bond lengths in the relaxed 5MC states of both [Fe(btbip)2]2+ and [Fe(bmip)2]2+ are very similar, the increase in ΔRax and ΔReq can largely be ascribed to the shorter initial Req (∼0.1 Å) bond length in the ground state of [Fe(bmip)2]2+.45
These observations provide the first unambiguous characterization of the excited MC state of an Fe-centered system with properties falling between those of traditional FeII SCO complexes and strong LFS complexes utilizing NHC ligands with increased MLCT lifetimes. It confirms the computational prediction that NHC compounds exhibit excited MC states where the minima are pushed further away from the GS along the main reaction coordinate (metal-to-ligand bond distance). Together with energy destabilization, this structural distortion of the scavenger MC states shortens their lifetime, and make them less accessible from the MLCT manifold, which in turn results in increased MLCT lifetimes. Hence, [Fe(btbip)2]2+ exhibits stronger geometric distortion in the 5MC state compared to traditional SCO systems; at the same time, the energy and structural distortion of the MC states are not large enough to remove the 5MC state from the MLCT deactivation cascade. Overall, the presented results show that the transition in photophysical properties between weak LFS and strong LFS Fe–NHC compounds manifest itself not only in the destabilization of the MC states, but also in the significantly different structural dynamics of these systems.
Conclusion
To summarize, the excited state relaxation following the MLCT excitation of [Fe(btbip)2]2+ was probed by TRWAXS with 100 ps time-resolution, allowing for the definite assignment of a 260 ps lifetime metal-centered quintet excited state as part of the MLCT relaxation pathway. The structural analysis of the excited state demonstrates that the 5MC state is significantly distorted compared to the GS, which is observed as unusually large differences in metal-to-ligand bond lengths in the two states. Thus, while the [Fe(btbip)2]2+ photocycle is mechanistically close to that of typical FeII SCO compounds, the large structural distortion of its 5MC state distinguishes the complex from traditional FeII SCO complexes. Since the observed distortion was previously indicated in DFT studies as one of the key factors of the success of the novel NHC compounds, these results provide new experimental insight into the MLCT deactivation pathways of the NHC family. We note that the combination of bulky tBu side-groups with the strong σ-donating NHC ligands allowed us to probe an interesting part of the excited state cascade that previously was inaccessible in related NHC complexes. These results are of fundamental interest in the context of recent discussions of the nature of short-lived MC states in FeII complexes with strong LFS.54,55 Overall, this work suggests that a characterization of the full deactivation cascade in other complexes with few-100 ps and faster GS recovery is necessary to fully characterize the rich and non-trivial photophysics of Fe complexes.More generally this work illustrates how TRWAXS on a photosensitive molecule in solution provides information not only on the transient structures, but also on the energies of short-lived excited species, which is traditionally a difficult task since most experiments are either tailored towards structure or energy sensitivity. The refinement procedure aided by DFT calculations used in this work will further expand the classes of systems for which TRWAXS can provide experimental determination of short-lived excited state structures, beyond systems with heavy atom pairs. We note that a key enabling factor in the direct identification of the 5MC state and in the high precision structural refinement is the availability of high-quality quasi-monochromatic TRWAXS data up to large scattering vectors, qmax = 11.5 Å−1. Moreover, TRWAXS can uniquely provide information about excited state energies by direct assessment of the amount of energy disposed into the solvent during excited state relaxation. Such information cannot be readily retrieved for MC states with optical methods, such as absorption or fluorescence spectroscopy due to the formally dipole-forbidden nature of the optical transitions between the GS and MC states which drastically reduces the interaction cross-section and, more importantly, because the relaxed MC states are geometrically inaccessible from vertical light excitations (Fig. 5). While the ΔE value obtained in this work is subject to some uncertainty, coupled with the advanced structural analysis, it provides an important stepping-stone for much more comprehensive explorations of excited state potential energy surfaces. Further improvements of the experimental setup in terms of stability and signal-to-noise should help in increasing the precision of the extracted energies. Additionally, careful investigation of the power, concentration and pump wavelength effects should make the quantification of ΔE more robust. Improvements in the cage modelling will also impact the accuracy of the energetic parameters since both solvation and solvent contributions are present primarily in the low-q region of the difference signal. The experimental quantification of the energy and structure of the short-lived 5MC state of [Fe(btbip)2]2+, provides a robust experimental tool for the direct validation and comparison of different quantum chemical methods, in particular the choice of functionals, to accurately predict the structure and energy of short-lived MC states in Fe complexes. Future systematic TRWAXS studies of FeII complexes will be able to capture the effect of the ligand structure on the kinetic, structural, and energetic aspects of charge transfer and spin transitions in this class of systems allowing for more detailed investigations of the role of the excited MC states in the MLCT deactivation process. This combined progress in experimental and theoretical capabilities will benefit not only the search for perspective earth-abundant photosensitizers, but also the advancement in the understanding of SCO compounds for future opto-magnetic materials.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The DTU-affiliated authors would like to gratefully acknowledge DANSCATT for funding the beam time efforts and the Danish Council of independent research grant DFF – 4002-00272. PP acknowledges financial support from the Knut and Alice Wallenberg Foundation as well as the Swedish Energy Agency (Energimyndigheten), as well as support from the Swedish national supercomputer facilities NSC and LUNARC. KSK gratefully acknowledges the support of the Carlsberg Foundation and the Danish Council for Independent Research.Notes and references
- C. Creutz, M. Chou, T. L. Netzel, M. Okumura and N. Sutin, J. Am. Chem. Soc., 1980, 102, 1309–1319 CrossRef CAS.
- J. K. McCusker, K. N. Walda, R. C. Dunn, J. D. Simon, D. Magde and D. N. Hendrickson, J. Am. Chem. Soc., 1993, 115, 298–307 CrossRef CAS.
- J. K. McCusker, A. L. Rheingold and D. N. Hendrickson, Inorg. Chem., 1996, 35, 2100–2112 CrossRef CAS.
- J. E. Monat and J. K. McCusker, J. Am. Chem. Soc., 2000, 122, 4092–4097 CrossRef CAS.
- C. Brady, J. J. McGarvey, J. K. McCusker, H. Toftlund and D. N. Hendrickson, in Spin Crossover in Transition Metal Compounds III, Springer Berlin Heidelberg, Berlin, Heidelberg, 2004, pp. 1–22 Search PubMed.
- E. A. Juban, A. L. Smeigh, J. E. Monat and J. K. McCusker, Coord. Chem. Rev., 2006, 250, 1783–1791 CrossRef CAS.
- A. L. Smeigh, M. Creelman, R. A. Mathies and J. K. McCusker, J. Am. Chem. Soc., 2008, 130, 14105–14107 CrossRef CAS PubMed.
- N. Huse, H. Cho, K. Hong, L. Jamula, F. M. F. de Groot, T. K. Kim, J. K. McCusker and R. W. Schoenlein, J. Phys. Chem. Lett., 2011, 2, 880–884 CrossRef CAS PubMed.
- W. Gawelda, A. Cannizzo, V.-T. Pham, F. van Mourik, C. Bressler and M. Chergui, J. Am. Chem. Soc., 2007, 129, 8199–8206 CrossRef CAS PubMed.
- C. Bressler, C. Milne, V.-T. Pham, A. Elnahhas, R. M. van der Veen, W. Gawelda, S. Johnson, P. Beaud, D. Grolimund, M. Kaiser, C. N. Borca, G. Ingold, R. Abela and M. Chergui, Science, 2009, 323, 489–492 CrossRef CAS PubMed.
- A. Cannizzo, C. J. J. Milne, C. Consani, W. Gawelda, C. Bressler, F. van Mourik and M. Chergui, Coord. Chem. Rev., 2010, 254, 2677–2686 CrossRef CAS.
- G. Auböck and M. Chergui, Nat. Chem., 2015, 7, 629–633 CrossRef PubMed.
- K. S. Kjær, W. Zhang, R. Alonso-Mori, U. Bergmann, M. Chollet, R. G. Hadt, R. W. Hartsock, T. Harlang, T. Kroll, K. Kubiček, H. T. Lemke, H. W. Liang, Y. Liu, M. M. Nielsen, J. S. Robinson, E. I. Solomon, D. Sokaras, T. B. van Driel, T.-C. Weng, D. Zhu, P. Persson, K. Wärnmark, V. Sundström and K. J. Gaffney, Struct. Dyn., 2017, 4, 44030 CrossRef PubMed.
- V. Balzani, G. Bergamini, S. Campagna and F. Puntoriero, in Photochemistry and Photophysics of Coordination Compounds I, ed. V. Balzani and S. Campagna, Springer Berlin Heidelberg, Berlin, Heidelberg, 2007, pp. 1–36 Search PubMed.
- K. Haldrup, W. Gawelda, R. Abela, R. Alonso-Mori, U. Bergmann, A. Bordage, M. Cammarata, S. E. Canton, A. O. Dohn, T. B. van Driel, D. M. Fritz, A. Galler, P. Glatzel, T. Harlang, K. S. Kjær, H. T. Lemke, K. B. Møller, Z. Németh, M. Pápai, N. Sas, J. Uhlig, D. Zhu, G. Vankó, V. Sundström, M. M. Nielsen and C. Bressler, J. Phys. Chem. B, 2016, 120, 1158–1168 CrossRef CAS PubMed.
- O. Kahn and C. J. Martinez, Science, 1998, 279(5347), 44–48 CrossRef CAS.
- A. Bousseksou, G. Molnár, P. Demont, J. Menegotto, A. Bousseksou, J. J. Mc-Garvey, K. Boukheddaden and F. Varret, J. Mater. Chem., 2003, 13, 2069–2071 RSC.
- A. Bousseksou, G. Molnár and G. Matouzenko, Eur. J. Inorg. Chem., 2004, 2004, 4353–4369 CrossRef.
- G. Molnár, S. Cobo, J. A. Real, F. Carcenac, E. Daran, C. Vieu and A. Bousseksou, Adv. Mater., 2007, 19, 2163–2167 CrossRef.
- J. Larionova, L. Salmon, Y. Guari, A. Tokarev, K. Molvinger, G. Molnár and A. Bousseksou, Angew. Chem., 2008, 120, 8360–8364 CrossRef.
- A. Bousseksou, G. Molnár, L. Salmon, W. Nicolazzi, F. Varret, H. Tokoro, C. Lecomte, J. S. Costa, J.-F. Létard, H. Paulsen, A. Bousseksou, E. Collet, J. Petersen, C. Becker and D. Ruch, Chem. Soc. Rev., 2011, 40, 3313 RSC.
- N. Huse, T. K. Kim, L. Jamula, J. K. McCusker, F. M. F. de Groot and R. W. Schoenlein, J. Am. Chem. Soc., 2010, 132, 6809–6816 CrossRef CAS PubMed.
- H. Cho, M. L. Strader, K. Hong, L. Jamula, E. M. Gullikson, T. K. Kim, F. M. F. de Groot, J. K. McCusker, R. W. Schoenlein and N. Huse, Faraday Discuss., 2012, 157, 463 RSC.
- K. Hong, H. Cho, R. W. Schoenlein, T. K. Kim and N. Huse, Acc. Chem. Res., 2015, 151021090255001 Search PubMed.
- J. Kim, K. H. Kim, K. Y. Oang, J. H. Lee, K. Hong, H. Cho, N. Huse, R. W. Schoenlein, T. K. Kim and H. Ihee, Chem. Commun., 2016, 52, 3734–3749 RSC.
- S. E. Canton, X. Zhang, L. M. Lawson Daku, A. L. Smeigh, J. Zhang, Y. Liu, C. J. Wallentin, K. Attenkofer, G. Jennings, C. A. Kurtz, D. Gosztola, K. Wärnmark, A. Hauser and V. Sundström, J. Phys. Chem. C, 2014, 118, 4536–4545 CAS.
- X. Zhang, M. L. Lawson Daku, J. Zhang, K. Suarez-Alcantara, G. Jennings, C. A. Kurtz and S. E. Canton, J. Phys. Chem. C, 2015, 119, 3312–3321 CAS.
- M. Pápai, G. Vankó, C. De Graaf and T. Rozgonyi, J. Chem. Theory Comput., 2013, 9, 509–519 CrossRef PubMed.
- G. Vankó, A. Bordage, M. Pápai, K. Haldrup, P. Glatzel, A. M. March, G. Doumy, A. Britz, A. Galler, T. A. Assefa, D. Cabaret, A. Juhin, T. B. van Driel, K. S. Kjær, A. O. Dohn, K. B. Moller, H. T. Lemke, E. Gallo, M. Rovezzi, Z. Németh, E. Rozsályi, T. Rozgonyi, J. Uhlig, V. Sundstrom, M. M. Nielsen, L. Young, S. H. Southworth, C. Bressler and W. Gawelda, J. Phys. Chem. C, 2015, 119, 5888–5902 Search PubMed.
- G. Vankó, T. Neisius, G. Molnár, F. Renz, S. Kárpáti, A. Shukla and F. M. F. de Groot, J. Phys. Chem. B, 2006, 110, 11647–11653 CrossRef PubMed.
- G. Vankó, A. Bordage, P. Glatzel, E. Gallo, M. Rovezzi, W. Gawelda, A. Galler, C. Bressler, G. Doumy, A. M. March, E. P. Kanter, L. Young, S. H. Southworth, S. E. Canton, J. Uhlig, G. Smolentsev, V. Sundström, K. Haldrup, T. B. van Driel, M. M. Nielsen, K. S. Kjaer and H. T. Lemke, J. Electron Spectrosc. Relat. Phenom., 2013, 188, 166–171 CrossRef.
- A. Hauser, in Spin Crossover in Transition Metal Compounds II, Springer Berlin Heidelberg, Berlin, Heidelberg, 2004, pp. 155–198 Search PubMed.
- A. Hauser, in Spin Crossover in Transition Metal Compounds I, ed. P. Gütlich and H. A. Goodwin, Springer Berlin Heidelberg, Berlin, Heidelberg, 2004, pp. 49–58 Search PubMed.
- A. Hauser, P. Gütlich, R. Hinek, H. Spiering and D. Schollmeyer, Chem.–Eur. J., 1996, 2, 1427–1434 CrossRef.
- J. Jeftic, R. Hinek, S. C. Capelli and A. Hauser, Inorg. Chem., 1997, 36, 3080–3087 CrossRef CAS PubMed.
- A. Hauser, C. Enachescu, M. L. Daku, A. Vargas and N. Amstutz, Coord. Chem. Rev., 2006, 250, 1642–1652 CrossRef CAS.
- A. Hauser, J. Chem. Phys., 1991, 94, 2741 CrossRef CAS.
- A. Hauser, A. Vef and P. Adler, J. Chem. Phys., 1991, 95, 8710 CrossRef CAS.
- W. Gawelda, V.-T. Pham, M. Benfatto, Y. Zaushitsyn, M. Kaiser, D. Grolimund, S. L. Johnson, R. Abela, A. Hauser, C. Bressler and M. Chergui, Phys. Rev. Lett., 2007, 98, 57401 CrossRef PubMed.
- G. G. Vankó, P. Glatzel, V.-T. Pham, R. Abela, D. Grolimund, C. N. Borca, S. L. Johnson, C. J. Milne and C. Bressler, Angew. Chem., Int. Ed. Engl., 2010, 49, 5910–5912 CrossRef PubMed.
- Y. Liu, P. Persson, V. Sundström and K. Wärnmark, Acc. Chem. Res., 2016, 49, 1477–1485 CrossRef CAS PubMed.
- W. Zhang, K. S. Kjær, R. Alonso-Mori, U. Bergmann, M. Chollet, L. A. Fredin, R. G. Hadt, R. W. Hartsock, T. Harlang, T. Kroll, K. Kubiček, H. T. Lemke, H. W. Liang, Y. Liu, M. M. Nielsen, P. Persson, J. S. Robinson, E. I. Solomon, Z. Sun, D. Sokaras, T. B. van Driel, T.-C. Weng, D. Zhu, K. Wärnmark, V. Sundström and K. J. Gaffney, Chem. Sci., 2017, 8, 515–523 RSC.
- T. C. B. Harlang, Y. Liu, O. Gordivska, L. A. Fredin, C. S. Ponseca Jr, P. Huang, P. Chábera, K. S. Kjær, H. Mateos, J. Uhlig, R. Lomoth, R. Wallenberg, S. Styring, P. Persson, V. Sundström and K. Wärnmark, Nat. Chem., 2015, 7, 883–889 CrossRef CAS PubMed.
- P. Chábera, Y. Liu, O. Prakash, E. Thyrhaug, A. El Nahhas, A. Honarfar, S. Essén, L. A. Fredin, T. C. B. Harlang, K. S. Kjær, K. Handrup, F. Ericson, H. Tatsuno, K. Morgan, J. Schnadt, L. Häggström, T. Ericsson, A. Sobkowiak, S. Lidin, P. Huang, S. Styring, J. Uhlig, J. Bendix, R. Lomoth, V. Sundström, P. Persson and K. Wärnmark, Nature, 2017, 543, 695–699 CrossRef PubMed.
- L. A. Fredin, M. Pápai, E. Rozsályi, G. Vankó, K. Wärnmark, V. Sundström and P. Persson, J. Phys. Chem. Lett., 2014, 5, 2066–2071 CrossRef CAS PubMed.
- L. A. Fredin, K. Wärnmark, V. Sundström and P. Persson, ChemSusChem, 2016, 9, 667–675 CrossRef CAS PubMed.
- S. G. Shepard, S. M. Fatur, A. K. Rappé and N. H. Damrauer, J. Am. Chem. Soc., 2016, 138, 2949–2952 CrossRef CAS PubMed.
- S. M. Fatur, S. G. Shepard, R. F. Higgins, M. P. Shores and N. H. Damrauer, J. Am. Chem. Soc., 2017, 139, 4493–4505 CrossRef CAS PubMed.
- Y. Liu, T. Harlang, S. E. Canton, P. Chábera, K. Suárez-Alcántara, A. Fleckhaus, D. A. Vithanage, E. Göransson, A. Corani, R. Lomoth, V. Sundström and K. Wärnmark, Chem. Commun., 2013, 49, 6412–6414 RSC.
- M. Pápai, T. J. Penfold and K. B. Møller, J. Phys. Chem. C, 2016, 120, 17234–17241 Search PubMed.
- L. A. Fredin, M. Pápai, E. Rozsályi, G. Vankó, K. Wärnmark, V. Sundström and P. Persson, J. Phys. Chem. Lett., 2014, 5, 2066–2071 CrossRef CAS PubMed.
- K. Kuhar, L. A. Fredin and P. Persson, J. Phys. Chem. B, 2015, 119, 7378–7392 CrossRef CAS PubMed.
- Y. Liu, K. S. Kjaer, L. A. Fredin, P. Chábera, T. Harlang, S. E. Canton, S. Lidin, J. Zhang, R. Lomoth, K.-E. Bergquist, P. Persson, K. Wärnmark and V. Sundström, Chemistry, 2014, 21, 3628–3639 CrossRef PubMed.
- L. L. Jamula, A. M. Brown, G. Dong and J. K. McCusker, Inorg. Chem., 2014, 53, 15–17 CrossRef CAS PubMed.
- A. K. C. Mengel, C. Förster, A. Breivogel, K. Mack, J. R. Ochsmann, F. Laquai, V. Ksenofontov and K. Heinze, Chem.–Eur. J., 2015, 21, 704–714 CrossRef CAS PubMed.
- Q. Sun, S. Mosquera-Vazquez, L. M. Lawson Daku, L. Guénée, H. A. Goodwin, E. Vauthey and A. Hauser, J. Am. Chem. Soc., 2013, 135, 13660–13663 CrossRef CAS PubMed.
- Q. Sun, S. Mosquera-Vazquez, Y. Suffren, J. Hankache, N. Amstutz, L. M. Lawson Daku, E. Vauthey and A. Hauser, Coord. Chem. Rev., 2015, 282, 87–99 CrossRef.
- Q. Sun, B. Dereka, E. Vauthey, L. M. Lawson Daku, A. Hauser, H. B. Schlegel, A. J. H. M. Meijer, J. A. Weinstein, R. Diller, L. Chamberlain, A. Mandel, L. Lilge and S. A. McFarland, Chem. Sci., 2017, 8, 223–230 RSC.
- H. Ihee, M. Wulff, J. Kim and S. Adachi, Int. Rev. Phys. Chem., 2010, 29, 453–520 CrossRef CAS.
- K. Hwan Kim, J. Kim, J. Hyuk Lee, H. Ihee, K. H. Kim, J. Kim, J. H. Lee and H. Ihee, Struct. Dyn., 2014, 1, 11301 CrossRef PubMed.
- M. Chergui and A. H. Zewail, ChemPhysChem, 2009, 10, 28–43 CrossRef CAS PubMed.
- M. Chergui and E. Collet, Chem. Rev., 2017, 117, 11025–11065 CrossRef CAS PubMed.
- C. S. Ponseca, P. Chábera, J. Uhlig, P. Persson and V. Sundström, Chem. Rev., 2017, 117, 10940–11024 CrossRef CAS PubMed.
- M. Wulff, A. Plech, L. Eybert, R. Randler, F. Schotte and P. Anfinrud, Faraday Discuss., 2003, 122, 13–26 RSC.
- J.-C. Labiche, O. Mathon, S. Pascarelli, M. A. Newton, G. G. Ferre, C. Curfs, G. Vaughan, A. Homs and D. F. Carreiras, Rev. Sci. Instrum., 2007, 78, 91301 CrossRef PubMed.
- H. Ihee, M. Lorenc, T. K. Kim, Q. Y. Kong, M. Cammarata, J. H. Lee, S. Bratos and M. Wulff, Science, 2005, 309, 1223–1227 CrossRef CAS PubMed.
- K. Haldrup, M. Christensen and M. Meedom Nielsen, Acta Crystallogr. Sect. A Found. Crystallogr., 2010, 66, 261–269 CrossRef CAS PubMed.
- E. A. Stern, Phys. Rev. B, 1993, 48, 9825–9827 CrossRef CAS.
- H. Ihee, M. Wulff, J. Kim and S. Adachi, Int. Rev. Phys. Chem., 2010, 29, 453–520 CrossRef CAS.
- K. Haldrup, G. Vankó, W. Gawelda, A. Galler, G. Doumy, A. M. March, E. P. Kanter, A. Bordage, A. Dohn, T. B. Van Driel, K. S. Kjær, H. T. Lemke, S. E. Canton, J. Uhlig, V. Sundström, L. Young, S. H. Southworth, M. M. Nielsen and C. Bressler, J. Phys. Chem. A, 2012, 116, 9878–9887 CrossRef CAS PubMed.
- K. S. Kjær, T. B. van Driel, J. Kehres, K. Haldrup, D. Khakhulin, K. Bechgaard, M. Cammarata, M. Wulff, T. J. Sørensen, M. M. Nielsen, K. S. Kjaer, T. B. van Driel, J. Kehres, K. Haldrup, D. Khakhulin, K. Bechgaard, M. Cammarata, M. Wulff, T. J. Sorensen and M. M. Nielsen, Phys. Chem. Chem. Phys., 2013, 15, 15003–15016 RSC.
- M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158 CrossRef CAS.
- E. Brémond and C. Adamo, J. Chem. Phys., 2011, 135, 24106 CrossRef PubMed.
- A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- K. Raghavachari and G. W. Trucks, J. Chem. Phys., 1989, 91, 1062–1065 CrossRef.
- G. Scalmani and M. J. Frisch, J. Chem. Phys., 2010, 132, 114110 CrossRef PubMed.
- E. Biasin, T. B. van Driel, K. S. Kjaer, A. O. Dohn, M. Christensen, T. Harlang, P. Chabera, Y. Liu, J. Uhlig, M. Pápai, Z. Németh, R. Hartsock, W. Liang, J. Zhang, R. Alonso-Mori, M. Chollet, J. M. Glownia, S. Nelson, D. Sokaras, T. A. Assefa, A. Britz, A. Galler, W. Gawelda, C. Bressler, K. J. Gaffney, H. T. Lemke, K. B. Møller, M. M. Nielsen, V. Sundström, G. Vankó, K. Wärnmark, S. E. Canton and K. Haldrup, Phys. Rev. Lett., 2016, 117, 13002 CrossRef PubMed.
- L. M. L. Daku and A. Hauser, J. Phys. Chem. Lett., 2010, 1, 1830–1835 CrossRef.
- E. Dova, A. F. Stassen, R. A. Driessen, E. Sonneveld, K. Goubitz, R. Peschar, J. G. Haasnoot, J. Reedijk and H. Schenk, Acta Crystallogr., Sect. B: Struct. Sci., 2001, 57, 531–538 CAS.
- S. Nozawa, T. Sato, M. Chollet, K. Ichiyanagi, A. Tomita, H. Fujii, S. Adachi and S. Koshihara, J. Am. Chem. Soc., 2010, 132, 61–63 CrossRef CAS PubMed.
- W. Gawelda, V.-T. Pham, R. M. van der Veen, D. Grolimund, R. Abela, M. Chergui and C. Bressler, J. Chem. Phys., 2009, 130, 124520 CrossRef CAS PubMed.
- J. A. Real, I. Castro, A. Bousseksou, M. Verdaguer, R. Burriel, M. Castro, J. Linares and F. Varret, Inorg. Chem., 1997, 36, 455–464 CrossRef CAS.
- J. Nance, D. N. Bowman, S. Mukherjee, C. T. Kelley and E. Jakubikova, Inorg. Chem., 2015, 54, 11259–11268 CrossRef CAS PubMed.
- M. Khalil, M. A. Marcus, A. L. Smeigh, J. K. McCusker, H. H. W. Chong and R. W. Schoenlein, J. Phys. Chem. A, 2005, 110, 38–44 CrossRef PubMed.
- Q. Kong, J. H. Lee, M. Lo Russo, T. K. Kim, M. Lorenc, M. Cammarata, S. Bratos, T. Buslaps, V. Honkimaki, H. Ihee and M. Wulff, Acta Crystallogr., Sect. A: Found. Crystallogr., 2010, 66, 252–260 CrossRef CAS PubMed.
- J. Davidsson, J. Poulsen, M. Cammarata, P. Georgiou, R. Wouts, G. Katona, F. Jacobson, A. Plech, M. Wulff, G. Nyman and R. Neutze, Phys. Rev. Lett., 2005, 94, 245503 CrossRef.
- Q. Kong, J. Kim, M. Lorenc, T. K. Kim, H. Ihee and M. Wulff, J. Phys. Chem. A, 2005, 109, 10451–10458 CrossRef CAS PubMed.
- J. Vincent, M. Andersson, M. Eklund, A. B. Wöhri, M. Odelius, E. Malmerberg, Q. Kong, M. Wulff, R. Neutze and J. Davidsson, J. Chem. Phys., 2009, 130, 154502 CrossRef PubMed.
- K. H. Kim, J. H. Lee, J. J. Kim, S. Nozawa, T. Sato, A. Tomita, K. Ichiyanagi, H. Ki, J. J. Kim, S. I. Adachi and H. Ihee, Phys. Rev. Lett., 2013, 110, 165505 CrossRef PubMed.
- K. H. Kim, H. Ki, J. H. Lee, S. Park, Q. Kong, J. Kim, J. Kim, M. Wulff and H. Ihee, Phys. Chem. Chem. Phys., 2015, 17, 8633–8637 RSC.
- K. Haldrup, T. Harlang, M. Christensen, A. Dohn, T. B. van Driel, K. S. Kjær, N. Harrit, J. Vibenholt, L. Guerin, M. Wulff and M. M. Nielsen, Inorg. Chem., 2011, 50, 9329–9336 CrossRef CAS PubMed.
- M. Christensen, K. Haldrup, K. Bechgaard, R. Feidenhans, Q. Kong, M. Cammarata, M. Lo Russo, M. Wulff, N. Harrit and M. M. Nielsen, J. Am. Chem. Soc., 2009, 131, 502–508 CrossRef CAS PubMed.
- K. Haldrup, A. O. Dohn, M. L. Shelby, M. W. Mara, A. B. Stickrath, M. R. Harpham, J. Huang, X. Zhang, K. B. Møller, A. Chakraborty, F. N. Castellano, D. M. Tiede and L. X. Chen, J. Phys. Chem. A, 2016, 120, 7475–7483 CrossRef CAS PubMed.
- C. Bressler, W. Gawelda, A. Galler, M. M. Nielsen, V. Sundström, G. Doumy, A. M. March, S. H. Southworth, L. Young and G. Vankó, Faraday Discuss., 2014, 171, 169–178 RSC.
- M. Reiher, O. Salomon and B. Artur Hess, Theor. Chim. Acta, 2001, 107, 48–55 CrossRef CAS.
- D. N. Bowman and E. Jakubikova, Inorg. Chem., 2012, 51, 6011–6019 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- M. Reiher, O. Salomon and B. Artur Hess, Theor. Chem. Acc., 2001, 107, 48–55 CrossRef CAS.
- O. Salomon, M. Reiher and B. A. Hess, J. Chem. Phys., 2002, 117, 4729–4737 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed.
- V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129–12137 CrossRef CAS.
- V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2004, 121, 11507 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7sc02815f |
| This journal is © The Royal Society of Chemistry 2018 |