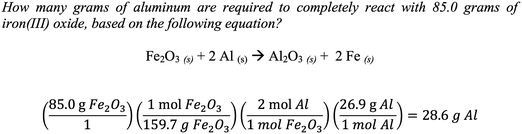The effect of teaching the entire academic year of high school chemistry utilizing abstract reasoning
Michael F. Z.
Page
 *,
Patrick
Escott
,
Maritza
Silva
and
Gregory A.
Barding
Jr.
*,
Patrick
Escott
,
Maritza
Silva
and
Gregory A.
Barding
Jr.
Chemistry and Biochemistry Department, California State Polytechnic University, Pomona, Pomona, CA 91768, USA. E-mail: mfpage@cpp.edu; Tel: +1 (909) 869-4533
First published on 7th February 2018
Abstract
This case study demonstrates the ability of high school chemistry students, with varying levels of math preparation, to experience learning-gains on state and district assessments as it relates to chemical reactions, thermodynamics, and kinetics. These advances were predicated on the use of a teaching style rooted in abstract reasoning. The methodology was presented to students and modeled by the instructor over an entire school year to reinforce key proportional relationships featured in the balanced chemical equation and related topics such as acids and bases, reaction rates, equilibrium, and conservation of matter. Despite the small sample size, there was a general increase in student success, indicated by a statistically significant difference between students receiving instruction rooted in concrete reasoning and students receiving instruction rich in abstract reasoning.
Introduction
In the psychology of human learning, proportional reasoning is widely recognized as an ability that signals a shift from concrete operational levels of thought to formal operational levels of thought (Piaget, 1972). Three decades of math education research also supports the development of proportional reasoning in two associated ways. First, the student's strategies to solve abstract problems become increasingly accurate and refined with age and experience. Second, more complex proportional problems can be solved (Tourniaire and Pulos, 1985). So as adolescent students transition from concrete arithmetic to the symbolic language of algebra, they develop abstract cognition essential for further advancement in science, technology, engineering, and mathematics (Susac et al., 2014).In most chemical education investigations of stoichiometry, a keen focus is often on the mole concept. Recently, Ramful and Narod (2014) identified that, in addition to the mole concept, many stoichiometry problems have multiple levels of proportionality that could prove increasingly difficult to solve. Generally, there are five levels of complexity involved in stoichiometric calculations including (a) the use of a simple mole ratio; (b) unit conversion and incorporation of mole ratios; (c) proportional relationships based on volume, the number of particles, or concentration; (d) utilizing various proportional relationships expressed in multiple reaction equations such as a chemical reaction followed by a titration or excess/limiting reagents; and (e) calculations in which one quantity or identity is unknown and must be determined. Furthermore, Scott (2012) compared high school students’ ability to solve analogous chemistry and mathematical questions. This study found that the mole concept is not the reason for poor success in solving problems. When difficult chemistry and math problems were solved, the math problem solutions were homogenous and often completed in an algorithmic fashion. Conversely, the more difficult chemistry questions were solved in a variety of fashions utilizing abstract reasoning. Therefore, higher-level abstract learning could be hindered if students rely on algorithms. In the US this is further complicated because a majority of chemistry textbooks present solving stoichiometric calculations using concrete reasoning (CR) that is guided by unit cancellation (Tykodi, 1987). This method of rote memorization (Dori and Hameiri, 2003) is highlighted in solved examples in seventeen contemporary textbooks reviewed by Cook and Cook (2005).
When employing concrete reasoning, a common mistake made by students is that they often invert the conversion factors; meaning a value that should be in the numerator is improperly placed in the denominator or vice versa. Furthermore, studies have shown that students who are able to properly use mole ratio coefficients, shown in Fig. 1, do not understand the chemical concepts that the balanced equation conveys (Nurrenbern and Pickering, 1987; Sanger, 2005).
In Fig. 2, the previous question is again solved, this time using abstract reasoning (Schmidt and Jingnéus, 2003; Page et al., 2012; Struck and Yerrick, 2013). Using the balanced molecular equation, a student can reason that 1 mole of Fe2O3 can completely react with 2 moles of Al. Then, using the molar masses of the starting materials [159.7 g mol−1 Fe2O3 and 26.9 g mol−1 Al], a student can deduce that 159.7 g of Fe2O3 can completely react with 53.8 g of Al (shown in the denominator). Finally, a proportional relationship can be used to solve for the unknown quantity that 28.6 grams of Al are required to completely react with iron(III) oxide. Chandrasegaran et al. (2009) found that average- and lower-achieving students actually benefit from instruction that highlights reasoning strategies rooted in the balanced equation. Furthermore, abstract reasoning can also be extended to solve problems dealing with concentrations, titrations, densities, percent masses, percent yields, solution stoichiometry, and gas laws since each of these concepts is based on a proportional relationship (Beichl, 1986; DeToma 1994; Cook and Cook, 2005). Based on the cognitive development of high school students and their need to gain expertise in abstract reasoning, it seems logical that the extent of chemical learning should be examined through the incorporation of abstract reasoning in the day-to-day science instructional delivery to students with varying math aptitudes and reasoning capabilities.
Aim of the study
A learning community of high school chemistry teachers collaborated to address how abstract reasoning could address achievement gaps among chemistry students enrolled in math courses of various levels. The central question that shaped the intervention was, “Can students who have diverse levels of math preparation be equally supported while solving calculations in an introductory chemistry course using proportions based on abstract reasoning (AR)?” Case study teachers agreed to alter how they solved in-class stoichiometric calculations even though it meant diverging from how they themselves learned how to perform such calculations as learners. This study details the results of implementing proportional relationships, over the entire year, to support high school students in all levels of math to successfully learn chemistry. This research followed an approved protocol within the Human Research Protection Program governed by the Instituitional Review Board at the University. This included the collection of parental (informed consent) and participant assent from students involved in the study (Protocol ID 11-154).Method
During the course of the academic year, both the school district and the state board measure how well students meet content learning goals through standardized assessments. The state exam is proctored towards the end of the school year and contains 60 chemistry questions, as shown in Table 1 (see on the Web Materials Understanding California's Standardized Testing and Reporting (STAR) Program). A total of 62% of the chemistry state assessment questions can be solved using AR. The district chemistry benchmark tests are proctored at scheduled intervals throughout the year and total a combined 138 questions. Following most US curriculum guides, AR can be applied to solve problems throughout the entire academic year. Conservation of Matter and Stoichiometry is introduced towards the end of the first semester, and in the second semester Kinetics and Thermodynamics and Chemical Reactions are points of emphasis.| Cluster | Area of emphasis | Number of questions on state exam | Percent of state exam |
|---|---|---|---|
| a Content questions that can be answered using abstract reasoning. Note: areas of emphasis that are underlined represent the content area description on the state exam, while the descriptions in parentheses represent the content area description of the corresponding items on the district benchmark assessments. | |||
| 1 | Atomic and Molecular Structure | 8 | 13.3 |
| (Atomic and Molecular Structure) | |||
| (Nuclear Process) | |||
| 2 | Chemical Bonds, Biochemistry | 9 | 15 |
| (Chemical Bonds) | |||
| (Organic Chemistry and Biochemistry) | |||
| 3 | Kinetics and Thermodynamics | 14a | 23.3a |
| (Gases and their Properties) | |||
| (Solutions) | |||
| (Chemical Thermodynamics) | |||
| 4 | Chemical Reactions | 13a | 21.7a |
| (Acids and Bases) | |||
| (Reaction Rates) | |||
| (Chemical Equilibrium) | |||
| 5 | Conservation of Matter and Stoichiometry | 10a | 16.7a |
| (Conservation of Matter and Stoichiometry) | |||
| 6 | Investigation and Experimentation | 6 | 10 |
| (Investigation and Experimentation) | |||
Prior to the intervention, two years of student assessment performances were collected for each instructor and served as individual control populations. Both case study teachers had taught chemistry for a minimum of five years and had previously taught their students using CR. The teachers also agreed to form a learning community consisting of chemistry faculty members and undergraduate thesis students to support and standardize their instructional methods of AR to model solving stoichiometric problems, gas laws, pH, solutions, thermodynamics, reaction rates, and equilibrium calculations. During the intervention, the treatment students received a full year of AR instruction during their chemistry course, whereas the control students had previously received instruction rooted in CR.
In the US, students traditionally matriculate sequentially through Algebra I, Geometry, and Algebra II, and then advance to various levels of calculus or statistics courses. Therefore, based on the state math exit exam, Teacher A instructed an advanced population of students who were in Summative Math courses or Algebra II as corequisites with chemistry [see Table 2]. At the time of the intervention, the school site had an Academic Performance Index (API) of 814 and 51% of the students were classified as socioeconomically disadvantaged. Teacher B instructed a proficient and passing population of students with a greater ratio of students enrolled in Algebra II or Geometry, which are less progressive courses. This school site had an API of 670 and 95% of the students were classified as socioeconomically disadvantaged (see on the Web Materials Pomona Unified School Accountability Report Card (SARC) Reports, 2013). The API is a three-year measure of academic preparation of the student body on statewide assessments across multiple disciplines. The calculation can range from a low 200 to a high score of 1000. The expected goal (determined by the state) is for schools to achieve an API of 800.
| Control population | Treatment population | |
|---|---|---|
| Note: [y = Advanced], [+ = Proficient], [T = Passing] (for more information, see on the Web Materials California High School Exit Examination and Understanding California's Standardized Testing and Reporting (STAR) Program). | ||
| Teacher A | ||
| Summative Math | n = 116 | n = 86 |
| State Math Exit Exam Average | 433y | 425y |
| Algebra II | n = 119 | n = 47 |
| State Math Exit Exam Average | 415y | 406y |
| Teacher B | ||
| Summative Math | n = 49 | n = 20 |
| State Math Exit Exam Average | 386+ | 399+ |
| Algebra II | n = 124 | n = 54 |
| State Math Exit Exam Average | 378T | 369T |
| Geometry | n = 38 | n = 5 |
| State Math Exit Exam Average | 371T | 366 T |
The study populations, shown in Table 2, met the following criteria: (i) students completed both the first and second semesters of the introductory year of chemistry with the same teacher; (ii) students completed all of the district benchmark chemistry and math corequisite exams, with one exception being granted to graduating seniors who had conflicting administrative activities during the period of the very last assessment; and (iii) students completed state chemistry and math corequisite assessments. The overall state and district performances of the students were compared by teachers and analyzed using the stats package in R, a free software environment for statistical computing and graphics with analysis of variance functions (R Core Team, 2016). One- and two-way ANOVA were carried out using the one-way.test and aov functions. A one-way ANOVA was used to evaluate the likelihood that the two teaching styles had an impact on student chemistry learning outcomes, assuming unequal variance. Additionally, a two-way ANOVA was used to evaluate if the math course corequisite (i.e. Summative Math, Algebra II, or Geometry) of the students influenced their chemistry performance based on the different teaching methods used within this investigation. Because of the small, unbalanced data set, the results obtained from the two-way ANOVA (see the Appendix) were only used qualitatively and assisted in determining if an additional study on a more robust sample size with equal variances was warranted.
Results and discussion
In the classroom of Teacher A it was demonstrated that the control and treatment students correctly answered approximately the same percentage of overall questions on both the state and district chemistry exams. On the state exam, the control and treatment populations correctly answered an average of 45.3 and 45.9 chemistry assessment items, respectively, which equate to an overall average score of ∼76% for both groups. The same groups correctly answered an average of 102.9 and 102.0 chemistry assessment items, respectively, on the combined district chemistry benchmark assessments, which also equates to an overall average score of ∼74% [see Table 3]. This result demonstrates that the control and treatment populations had similar overall performances in the course, but includes material not directly influenced by AR, and was therefore not evaluated for significance within this study.| Control population average scores | Treatment population average scores | |
|---|---|---|
| Teacher A | ||
| Note: values indicate questions answered correctly. Standard deviation on the district benchmarks could not be calculated since graduating students in the populations are not required to participate in the final assessment in the second semester due to administrative conflicts. | ||
| State Chemistry Assessment (Total 60 Questions) | 45.3/60 (±7.6) | 45.9/60 (±7.8) |
| District Chemistry Assessment (Total 138 Questions) | 102.9/138 | 102.0/138 |
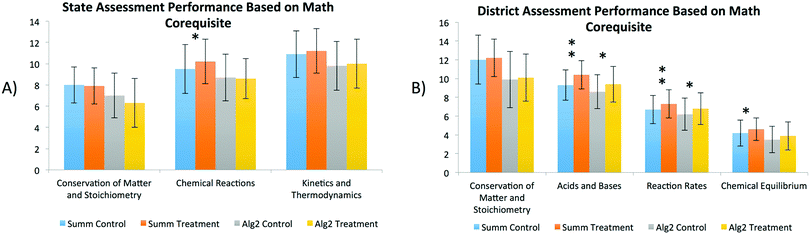
The chemistry proficiencies of various subset populations were also analyzed. In Fig. 3A, chemistry students in the treatment population, who were co-enrolled in Summative Math courses, demonstrated significant learning gains over the control as it pertained to Chemical Reactions (on the State Assessment). The same population of treatment students also had significant gains in the content areas of Acid and Bases, Reaction Rates, and Chemical Equilibrium during the district assessments when compared with the associated control (see Fig. 3B). Similarly, chemistry students in the treatment group, who were enrolled in Algebra II, demonstrated significant gains compared with the associated control on the district assessments in the areas of Acid and Bases and Reaction Rates. Although chemistry gains of students co-enrolled in Algebra II were not as dramatic as those of the higher-level Summative Math students, both treatment populations experienced learning enhancements correlated with receiving instruction rich in AR. The exact p-values of each one-way ANOVA regarding the population of Teacher A can be found in Table 5 in the Appendix.
In the classroom of Teacher B it was also demonstrated that the control and treatment students answered a similar percentage of overall questions correctly on both the state and district chemistry exams. On the state exam, the control and treatment populations correctly answered an average of 26.1 and 27.0 chemistry assessment items, respectively, yielding an overall average score of ∼44% for both populations. The same groups answered an average of 66.3 and 63.1 assessment questions, respectively, netting a similar overall average score of ∼47% on the district benchmark assessments [see Table 4]. Likewise, this result also demonstrates that the control and treatment populations had similar overall performances in the course, but includes material not directly influenced by AR, and was therefore not evaluated for significance within this study.
| Control population average scores | Treatment population average scores | |
|---|---|---|
| Teacher B | ||
| Note: values indicate questions answered correctly. Standard deviation on the district benchmarks could not be calculated since graduating students in the populations are not required to participate in the final assessment in the second semester due to administrative conflicts. | ||
| State Chemistry Assessment (Total 60 Questions) | 26.1/60 (±7.2) | 27.0/60 (±7.9) |
| District Chemistry Assessment (Total 138 Questions) | 66.3/138 | 63.1/138 |
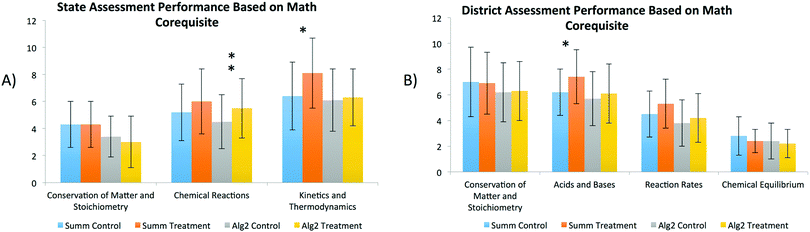
Chemistry students in the treatment population, who were co-enrolled in Summative Math courses, maintained or exceeded learning gains compared to the control. In Fig. 4, significant gains were highlighted for the treatment students who were co-enrolled in Summative Math in the content areas of Kinetics and Thermodynamics (state exam) and Acid and Bases (district assessment). Likewise, chemistry students in the treatment population, who were enrolled in Algebra II, demonstrated a similar trend when compared with the associated control on the state test in the area of Chemical Reactions. Although gains of students, co-enrolled in Algebra II, again were not as overwhelming as the Summative Math students, both treatment populations did still experience learning enhancements. The exact p-values of each one-way ANOVA regarding the population of Teacher B can be found in Table 6 in the Appendix.
The increased capacity of chemistry content by the students was collaborated in the transcribed reflections of both teachers during the final program evaluation.
[Teacher A] I was apprehensive of teaching the new AR method, but once I saw how it worked, I found it superior to CR because it shows the process of forming relationships. This was key because it did not encourage a blind focus on the units by the students. I also felt supported based on the work of the learning community. What I have found over the past few years is that all my students learn stoichiometry now. This problem-solving strategy remains relevant as we cover molarity, gas laws, and equilibrium in the second semester. Over the years, the vast majority of my Advance Placement chemistry students (not included in this intervention) switch to AR once they gain confidence, especially when solving limiting and excess reagent calculations. There are still times when a concrete approach makes more sense, for example when there is a multi-step conversion, but I have students who will still find a way to AR since it is extremely logical.
[Teacher B] By solving stoichiometry calculations using AR, this method makes the chemistry curriculum more accessible to students of diverse backgrounds and varying levels of math preparedness. The success of the method can be attributed to the visual nature of the relationships. The relationships between mass, moles, and equation coefficients are a pivotal part of introducing the strategy that aids all students to identify the imbedded ratios and proportionality of the balanced chemical equation. Ultimately, students rely on valid relationships in order to solve calculations.
Conclusions
This study suggests that instruction that emphasizes Abstract Reasoning supports the chemistry-based learning of students enrolled in higher-level Summative Math (Pre-calculus, Calculus, or Statistics) and Algebra II alike. The modest gains of the students enrolled in Algebra II were replicated in two different school sites from the same district in various subcategories on both the state and district assessments. This improvement of the lower-level math students through AR is supported by the findings of Chandrasegaran et al. (2009). Therefore, solving multiple types of numerical problems utilizing a consistent model of reasoning, rooted in relationships displayed in a balanced chemical equation, supports students with various math capabilities and formal operational levels of thought.Although advanced math students demonstrated the highest levels of chemistry competencies, this classroom intervention allowed greater opportunity for all students to (i) improve their abstract reasoning skills through the construction of valid proportions and (ii) solve a range of problems building on valid proportions as it relates to chemical reactions, pH, thermodynamics, kinetics, and equilibrium. This work is timely as the US is currently modifying its framework of science education to align with the Next Generation Science Standards (National Research Council, 2012, p. 75). This work suggests that slight gains can be realized through the use of AR in chemical instruction. In the US, this represents an innovation that may not be realistic immediately on a grand scale. However, greater long-term understanding on the part of the student could be further analyzed if this pilot study longitudinally extends to explore if the gains in these high school students, utilizing a small sample of teachers in diverse socioeconomic environments, can be replicated across an entire school district and even to the university-level curriculum.
Conflicts of interest
There are no conflicts to declare.Appendix
Results of each ANOVA are reported herein to evaluate the likelihood that varying teaching styles have an impact on student chemistry learning outcomes, assuming unequal variance.Results and discussion
Two-way ANOVA: in Tables 5 and 6, slight increases in the chemistry learning of students were observed. Of note to this study is that the lower-level Algebra II math students in two different socio-economic environments in the same school district experienced learning gains in content areas utilizing with Abstract Reasoning. A two-way ANOVA was performed to determine if the math level had an effect on the magnitude of improvement due to the AR method. All but one of these effects, shown below, were found to be insignificant. The interaction effects largely suggest that the math level of the students did not impact the improvement caused by the new curriculum. Ultimately, it would be difficult to draw hard conclusions from the two-way ANOVA results based on the vastly unbalanced population sizes (Landsheer and van den Wittenboer, 2015), and further study with a larger, balanced data set is necessary to confirm these results.| Teacher A state assessment results (Summative Math) | Teacher A state assessment results (Algebra II) | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Conservation of Matter and Stoichiometry | Chemical Reactions | Kinetics and Thermodynamics | Conservation of Matter and Stoichiometry | Chemical Reactions | Kinetics and Thermodynamics | |
| (10 Questions) | (13 Questions) | (14 Questions) | (10 Questions) | (13 Questions) | (14 Questions) | |
| [p-Value < 0.05 statistically relevant] Summative Math Control n = 116; Summative Math Treatment n = 86; Algebra II Control n = 119; Algebra II Treatment n = 47. | ||||||
| Control population (aver. score) | 8.0 | 9.5 | 10.9 | 7.0 | 8.7 | 9.8 |
| Treatment population (aver. score) | 7.9 | 10.2 | 11.2 | 6.3 | 8.6 | 10.0 |
| One-way ANOVA | F(1, 186) = 0.28, p = 0.60 | F(1, 191) = 5.48, p = 0.02 | F(1, 189) = 1.42, p = 0.24 | F(1, 78) = 3.09, p = 0.08 | F(1, 97) = 0.13, p = 0.71 | F(1, 84) = 0.21, p = 0.65 |
| Teacher A district assessment results (Summative Math) | Teacher A district assessment results (Algebra II) | |||||||
|---|---|---|---|---|---|---|---|---|
| 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | |
| Conservation of Matter and Stoichiometry | Acids and Bases | Reaction Rates | Chemical Equilibrium | Conservation of Matter and Stoichiometry | Acids and Bases | Reaction Rates | Chemical Equilibrium | |
| (15 Questions) | (12 Questions) | (9 Questions) | (6 Questions) | (15 Questions) | (12 Questions) | (9 Questions) | (6 Questions) | |
| Control population (aver. score) | 12.0 | 9.3 | 6.7 | 4.2 | 9.9 | 8.6 | 6.2 | 3.5 |
| Treatment population (aver. score) | 12.2 | 10.4 | 7.3 | 4.6 | 10.1 | 9.4 | 6.8 | 3.9 |
| One-way ANOVA | F(1, 196) = 0.32, p = 0.57 | F(1, 188) = 23.7, p = 2.4 × 10−6 | F(1, 182) = 8.60, p = 3.8 × 10−3 | F(1, 191) = 4.23, p = 0.04 | F(1, 100) = 0.24, p = 0.63 | F(1, 83) = 6.66, p = 0.01 | F(1, 87) = 5.01, p = 0.03 | F(1, 79) = 2.62, p = 0.11 |
| Teacher B state assessment results (Summative Math) | Teacher B state assessment results (Algebra II) | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Conservation of Matter and Stoichiometry | Chemical Reactions | Kinetics and Thermodynamics | Conservation of Matter and Stoichiometry | Chemical Reactions | Kinetics and Thermodynamics | |
| (10 Questions) | (13 Questions) | (14 Questions) | (10 Questions) | (13 Questions) | (14 Questions) | |
| [p-Value < 0.05 statically relevant] Summative Math Control n = 49; Summative Math Treatment n = 20; Algebra II Control n = 124; Algebra II Treatment n = 54. | ||||||
| Control population (aver. score) | 4.3 | 5.2 | 6.4 | 3.4 | 4.5 | 6.1 |
| Treatment population (aver. score) | 4.3 | 6.0 | 8.1 | 3.0 | 5.5 | 6.3 |
| One-way ANOVA | F(1, 35) = 0.02, p = 0.90 | F(1, 32) = 1.59, p = 0.22 | F(1, 33) = 5.70, p = 0.02 | F(1, 85) = 2.32, p = 0.13 | F(1, 94) = 8.22, p = 5.1 × 10−3 | F(1, 109) = 0.41, p = 0.52 |
| Teacher B district assessment results (Summative Math) | Teacher B district assessment results (Algebra II) | |||||||
|---|---|---|---|---|---|---|---|---|
| 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | |
| Conservation of Matter and Stoichiometry | Acids and Bases | Reaction Rates | Chemical Equilibrium | Conservation of Matter & Stoichiometry | Acids and Bases | Reaction Rates | Chemical Equilibrium | |
| (15 Ques.) | (12 Ques.) | (9 Ques.) | (6 Ques.) | (15 Ques.) | (12 Ques.) | (9 Ques.) | (6 Ques.) | |
| Control population (aver. score) | 7.0 | 6.2 | 4.5 | 2.8 | 6.2 | 5.7 | 3.8 | 2.4 |
| Treatment population (aver. score) | 6.9 | 7.4 | 5.3 | 2.5 | 6.3 | 6.1 | 4.2 | 2.2 |
| One-way ANOVA | F(1, 38) = 6.0 × 10−3, p = 0.94 | F(1, 30) = 4.22, p = 0.05 | F(1, 33) = 2.12, p = 0.15 | F(1, 53) = 1.43, p = 0.24 | F(1, 86) = 0.06, p = 0.81 | F(1, 77) = 1.10, p = 0.30 | F(1, 87) = 1.26, p = 0.26 | F(1, 100) = 0.93, p = 0.34 |
The interaction effects below describe the effect of the students’ math level on the treatment compared to the control population presented in Table 5:
Column #1 versus #4: F(1, 1) = 4.33, p = 0.04 Column #2 versus #5: F(1, 1) = 2.78, p = 1.00
Column #3 versus #6: F(1, 1) = 1.46, p = 0.23
Column #7 versus #11: F(1, 1) = 5.3 × 10−3, p = 0.94 Column #8 versus #12: F(1, 1) = 0.61, p = 0.43
Column #9 versus #13: F(1, 1) = 2.8 × 10−3, p = 0.96 Column #10 versus #14: F(1, 1) = 7.6 × 10−3, p = 0.93
The interaction effects below describe the effect of the students’ math level on the treatment compared to the control population presented in Table 6:
Column #1 versus #4: F(1, 1) = 0.56, p = 0.45 Column #2 versus #5: F(1, 1) = 3.76, p = 0.05
Column #3 versus #6: F(1, 1) = 1.56, p = 0.21
Column #7 versus #11: F(1, 1) = 5.4 × 10−3, p = 0.82 Column #8 versus #12: F(1, 1) = 1.89, p = 0.17
Column #9 versus #13: F(1, 1) = 0.68, p = 0.40 Column #10 versus #14: F(1, 1) = 0.21, p = 0.65
Acknowledgements
The authors would like to thank Christiana Duckett, Cynthia Hofferth, Stephanie Baker (Pomona United School District), and Dr. Edward Walton (Cal Poly Pomona) for their assistance in the completion of this study.Notes and references
- Beichl G., (1986), Unit basis – a neglected problem-solving technique, J. Chem. Educ., 63, 146–147.
- California High School Exit Examination (CAHSEE Results), https://www.cde.ca.gov/nr/ne/yr13/yr13rel78atta.asp date accessed 1/31/18.
- Chandrasegaran A. L., Treagust D. F., Waldrip B. G. and Chandrasegaran A., (2009), Students’ dilemmas in reaction stoichiometry problem solving: deducing the limiting reagent in chemical reactions, Chem. Educ. Res. Pract., 10, 14–23.
- Cook E. and Cook R., (2005), Cross-proportions: a conceptual method of developing quantitative problem-solving skills, J. Chem. Educ., 82, 1187–1189.
- DeToma R., (1994), Symbolic algebra and stoichiometry, J. Chem. Educ., 71, 568–570.
- Dori Y. and Hameiri M., (2003), Multidimensional analysis system for quantitative chemistry problems: symbol, macro, micro, and process aspect, J. Res. Sci. Teach., 40, 278–302.
- Landsheer J. A. and van den Wittenboer G. (2015), Unbalanced 2 × 2 factorial designs and the interaction effect: a troublesome combination, PLoS One, 10, 1–18.
- National Research Council, (2012), A Framework for K-12 Science Education: Practices, Crosscutting Concepts and Core Ideas, Washington, DC: National Academies Press.
- Nurrenbern S. and Pickering M., (1987), Concept learning versus problem solving: is there a difference? J. Chem. Educ., 64, 508–510.
- Page M., Guevara C. and Walton E., (2012), Concept based instruction for stoichiometry: the balanced molecular equation and proportional reasoning, Office of Research on Teaching in the Disciplines Background Research Paper No. 32, http://education.ua.edu/wp-content/uploads/2014/01/Background-Research-Paper-No.-32.pdf date accessed 1/31/18.
- Piaget J., (1972), Intellectual evolution from adolescence to adulthood, Hum. Dev., 15, 1–12.
- Pomona Unified School Accountability Report Card (SARC) Reports, (2013), Diamond Ranch High School, https://api.cde.ca.gov/Acnt2014/apiavgSch.aspx?allcds=19649071995901 date accessed 1/31/18, Ganesha High School https://api.cde.ca.gov/Acnt2014/apiavgSch.aspx?allcds=19649071933175 date accessed 1/31/18.
- R Core Team, (2016), R: a language and environment for statistical computing, R Foundation for Statistical Computing, Vienna, Austria.
- Ramful A. and Narod F. B., (2014), Proportional reasoning in the learning of chemistry: levels of complexity, Math. Educ. Res. J., 26, 25–46.
- Sanger M., (2005), Evaluating students’ conceptual understanding of balanced equations and stoichiometric ratios using a particulate drawing, J. Chem. Educ., 82, 131–134.
- Schmidt H. and Jingnéus C., (2003), Students’ strategies in solving algorithmic stoichiometry problems, Chem. Educ. Res. Pract., 4, 305–317.
- Scott F. J., (2012), Is Mathematics to blame? An investigation into high school students’ difficulty in performing calculations in chemistry, Chem. Educ. Res. Pract., 13, 330–336.
- Struck B. and Yerrick R., (2013), Bill's box: a simple and effective approach to stoichiometry, The Science Teacher, 80, 44–50.
- Susac A., Bubic A., Vrbanc A. and Planinic M., (2014), Development of abstract mathematical reasoning: the case of algebra, Front Hum Neurosci., 8, 1–10.
- Tourniaire F. and Pulos S., (1985), Proportional reasoning: a review of the literature, Educational Studies in Mathematics, 16, 181–204.
- Tykodi R., (1987), Reaction stoichiometry and suitable “coordinate systems”, J. Chem. Educ., 64, 958–960.
- Understanding California's Standardized Testing and Reporting (STAR) Program, http://www.ed-data.k12.ca.us/Pages/Understanding-the-STAR.aspx date accessed 1/31/18.
| This journal is © The Royal Society of Chemistry 2018 |