Peer learning as a tool to strengthen math skills in introductory chemistry laboratories

Abstract

Math skills vary greatly among students enrolled in introductory chemistry courses. Students with weak math skills (algebra and below) tend to perform poorly in introductory chemistry courses, which is correlated with increased attrition rates. Previous research has shown that retention of main ideas in a peer learning environment is greater when partners have dissimilar abilities. Therefore, in an effort to improve student learning outcomes, we implemented peer learning interventions in our introductory chemistry laboratories to determine if math skills were enhanced when partners differed in math ability. Student performance and attitudes were analyzed in laboratory sections consisting of instructor-assigned partners who differed in math ability, compared to sections where students self-selected a partner. Students who were assigned math partners of different ability showed an 8% improvement in chemistry math concepts compared to no improvement among those who self-selected a partner, as assessed using pre- and post-math tests. Mathematical learning gains were particularly large (16%) for those students in the 50th percentile of math performance. Students also reported a significantly more positive attitude change about working with others compared to students who self-selected a partner. In addition, assigned students demonstrated a more positive shift in self-concepts such as chemistry knowledge and laboratory skills. This study illustrates that peer learning can serve as a useful and easy-to-implement tool to strengthen math skills and improve student attitudes in introductory chemistry laboratories.

---

Introduction and theoretical framework

Math competency and introductory chemistry success

Previous work has shown that an increase in math competency increases success in introductory chemistry courses (also referred to as general chemistry in the United States), not only by improving student learning outcomes, but also overall retention in chemistry courses (Donovan and Wheland, 2009). Data from the early 1960s described a testing program to predict success or failure in the first semester of university general chemistry. This testing program focused on chemistry content, arithmetic, and algebra skills. It later became known as the Toledo placement exam (Hovey and Krohn, 1958; Hovey and Krohn, 1963). A similar exam was validated by Russell to diagnose areas of student improvement in the general chemistry curriculum with a focus on math skills (Russell, 1994). The importance of a strong math foundation is further emphasized by studies that demonstrate even simple math interventions can have profound outcomes for student competencies in general chemistry (Genyea, 1983; Bohning, 1984). Introductory chemistry students themselves recognize the importance of math to the subject of chemistry yet admit that they are not confident in their math skills (Johnston et al., 2016).

Unfortunately, failure and withdrawal rates in introductory university chemistry courses continue to remain high, and efforts to minimize these events have been well-documented (Rowe, 1983; Wagner et al., 2002; Popejoy and Asala, 2013). In the United States, there are no benchmarks for chemistry readiness at the university level. However, a number of studies have reported a strong, positive correlation between math scores on standardized United States college entrance exams such as the SAT (Scholastic Assessment Test) or ACT (American College Test) and first-year college student chemistry grades, success, and retention (Pickering, 1975; Ozsogomonyan and Loftus, 1979; Spencer, 1996; Chambers and Blake, 2007; Donovan and Wheland, 2009). These exams specifically test for competency in geometry, algebra, trigonometry, general problem solving and conversions, similar to Mathematical Readiness tests (Hodgen et al., 2010). Therefore, many United States universities utilize a minimum ACT or SAT math score for meeting the prerequisite for introductory chemistry courses. In 2017, the mean SAT math score in the United States was 527 (range: 200–800) (CollegeBoard, 2017). Students enter college with a range of SAT math scores and likewise earn a range of scores in general chemistry. However, students earning SAT math scores in the lower range (<550) earn relatively lower grades in general chemistry (Pickering, 1975; Ozsogomonyan and Loftus, 1979; Spencer, 1996; Chambers and Blake, 2007; Donovan and Wheland, 2009).

Peer learning in heterogeneous groups

This wide range of math scores creates a heterogeneous group of students in introductory chemistry courses. Therefore, we investigated peer learning as a strategy to strengthen math abilities in weak math students. Peer learning can be an effective pedagogical technique and has been applied to many disciplines (Johnson et al., 1981; Slavin, 1983; Bossert, 1988). It involves students learning directly from their peers, rather than from the instructor. This methodology is different from peer instruction where one student has the primary role of peer leader or teacher. In this case, a student leader facilitates an activity while the other peer(s) assume(s) the role of the student (Boud et al., 2006). Peer instruction has been used in chemistry laboratory courses at the university level (McCreary et al., 2006) and high school/secondary school level (Ding and Harskamp, 2011). Furthermore, peer instruction has been implemented to strengthen math skills (Kramarski and Mevarech, 2003; Hooker, 2011). In these settings, students who worked with their peers exhibited higher learning gains than students who worked individually (Kramarski and Mevarech, 2003; McCreary et al., 2006; Ding and Harskamp, 2011; Hooker, 2011). As with peer instruction, there are few reports on peer learning in chemistry laboratories (Shibley and Zimmaro, 2002; Carr, 2013). Of particular interest, results of using peer learning to strengthen chemistry-specific math skills are lacking.

Student involvement in peer learning strengthens many skill sets that have been identified as promoting lifelong learning. Boud et al. listed these as collaborative skills, critical thinking skills, communication skills, and learning to learn (Boud et al., 2006). Many careers require these same skill sets, so it is imperative to foster those skills early to prepare students for the work place. Instructors stress the need for working together, critically thinking about experiments, communicating findings clearly and concisely, and identifying better ways to study and apply knowledge. Therefore, implementing an evidence-based practice like peer learning has the potential to engage students in practicing these skill sets on a regular basis.

Many investigators have analyzed heterogeneous classrooms and reported ways in which some form of peer learning can lead to larger learning gains compared to students in homogenous groups (Larson et al., 1984; Cohen and Lotan, 1995; Fuchs et al., 1997). Structuring this heterogeneity, though, is not without its own challenges. Cohen and colleagues have applied the Expectation States Theory (Berger et al., 1966) in their work on interracial interactions (reviewed in (Cohen, 1982)). Briefly, this theory describes how high-status individuals come to dominate in a group situation. Some of the status characteristics within a group include gender, race, age, as well as abilities and skills related to the task at hand. In a classroom or laboratory setting, a student who recognizes that he or she has a higher ability may dominate and contribute to the partnership unequally (Dembo and McAuliffe, 1987). Several reports have also shown that some low achieving students do not reach their maximum potential when working with a high achiever because they perceive a difference in academic ability (Dembo and McAuliffe, 1987; Cohen and Lotan, 1997). Therefore, student abilities must be carefully considered in order to maximize learning in these heterogeneous peer groups. While our study specifically examines heterogeneity in terms of academic ability, academic level (Miller et al., 2012), family income (Fuchs et al., 1997), and other factors could be taken into account.

We have previously used peer learning effectively in a laboratory setting when partners were assigned based on differences in academic level (Miller et al., 2012). Undergraduate students who were assigned to work with graduate students in the same biotechnology course met their learning outcomes while performing significantly better on laboratory reports compared to undergraduates who worked with other undergraduates. In addition, these heterogeneous pairs had more positive attitudes about working with a laboratory partner, regardless if their assigned partner had relatively more or less laboratory experience. Furthermore, the vast majority of students reported equal contributions to the laboratory work within their partnership. In a separate peer learning study, a group-centered testing scheme was analyzed (Srougi et al., 2013). Critical thinking skills and attitudes were compared between students who chose their own teams and students in instructor-assigned teams. Formation of these teams was based on various levels of achievement on a previous exam. Students in instructor-assigned teams performed significantly better on the final exam, and lower-performing students in these teams benefitted from increased retention of the material. Furthermore, the majority of students reported that they were pleased with their group dynamics, both in the self-selected and assigned teams.

Part of the success of a classroom intervention is measured not only by an increase in student achievement (the cognitive domain), but also by a positive change in mindset as it pertains to their performance in an area of knowledge, defined as self-concept (Beane and Lipka, 1986; Marsh and Debus, 1991). The analysis of chemistry student's self-concepts and attitudes is well-documented (Shibley and Zimmaro, 2002; Bauer 2005; Duran Gisbert and Monereo Font, 2008; Ding and Harskamp, 2011). Interestingly, several groups in different disciplines reported that participation in peer learning interventions promoted students’ self-concepts (Duran Gisbert and Monereo Font, 2008), and more generally, their attitudes (Shibley and Zimmaro, 2002; Ding and Harskamp, 2011; Miller et al., 2012).

Therefore, our research focuses on utilizing peer learning partnerships of dissimilar math skills to strengthen students’ math skills and self-concepts in an introductory university chemistry course, similar to what has been implemented at the primary and secondary school (K-12) level (Fuchs et al., 1998; Kramarski and Mevarech, 2003; Esmonde, 2009). The following research questions guided this study:

(1) Will assigning partnerships consisting of a high math-scoring student and a low math-scoring student increase students’ chemistry-specific math performance on a variety of assessment methods?

(2) Will this peer learning intervention improve students’ self-concepts concerning chemistry and math as measured by anonymous surveys, compared to students in self-selected partnerships?

This novel approach to improving introductory chemistry math performance will add to the knowledge generated from educational research focused on first year university math (Davidson, 1990), especially chemistry-focused math.

Methodology

Student demographics

All student participants in this study were 18 years or older and were enrolled in the first semester of an introductory chemistry laboratory during one of two consecutive fall semesters at a four-year, private university in the United States. Each semester consists of approximately 16 weeks of instruction. A total of ten sections of the course were involved in the study. This course was for first and second year non-chemistry and non-biochemistry majors. The lecture component was a separate, co-requisite course. Student participants in the laboratory course thus represented a cross-section from several lecture sections offered by different instructors at different days and times. Participation was completely optional, and students completed consent forms during the first week of class. Incentive to participate consisted of one bonus point on the final exam. Those who did not consent to the study or who were not present the first day of class to complete the consent form were given an alternative bonus question also worth one extra point on the final exam. The university's Institutional Review Board (IRB) approved this protocol (#201412-317) after an expedited review.

Instructor information

Four instructors were involved in this study. Two instructors in Fall 2015 each taught two sections of the laboratory course (one control and one experimental section each). In Fall 2016, two additional instructors each taught two sections of the same laboratory course (one control and one experimental section each). Three of the four instructors were tenure-track faculty, while the fourth was an adjunct faculty member. All instructors were members of the university's Chemistry Department and had similar educational and training backgrounds. This included doctoral degrees, post-doctoral training, as well as similar years of teaching experience in higher education. Undergraduate teaching assistants were utilized in each section to answer student questions and aid in restocking materials and reagents. These assistants, however, did not assess any student work.

Student learning objectives

Expectations in this course were clearly detailed in the syllabus, including a list of student learning objectives.

Upon completion of this course, students should be able to:

(1) Understand and successfully follow written laboratory procedures

(2) Perform the various chemistry laboratory methods and techniques necessary for completion of experiments and collection of experimental data

(3) Make experimental observations and formulate logical conclusions based on them

(4) Know and be able to apply the mathematics required in chemistry and for calculation of accurate experimental results

Quantitative assessment methods

Student learning objectives were measured by a number of assessment methods. All sections of the course completed the same laboratory experiments in Fall 2015. Slight modifications in laboratory experiments occurred during Fall 2016, but 8 out of 11 chemical concepts were identical between the two semesters. Importantly, all math concepts analyzed were identical. All sections of the course used the same assessment methods. Peers worked together in a relatively unstructured way, without instructors assigning any roles. At the beginning of each weekly laboratory meeting, students’ understanding of the safety issues and fundamental concepts surrounding the laboratory (objective 1) were assessed with short pre-laboratory quizzes. These lower-order Bloom's taxonomy questions were primarily true/false and multiple-choice formats and were utilized to encourage students to read the laboratory procedures in preparation for class. Students completed these assessments individually in class with access only to a calculator. One week after completing a laboratory, students turned in a worksheet. These worksheets were completed in collaboration with the laboratory partner, and one worksheet was turned in per student. Each student was required to record experimental data, perform necessary calculations, draw conclusions based on that data, and discuss possible sources of error. Instructors and teaching assistants did not immediately intervene to help laboratory partners complete this work. These worksheets assessed objectives 1–4 (see above). At the end of the semester, each student turned in a formal laboratory report on the final experiment. This method assessed objectives 1–4.

Midterm and final exams were also administered to each student to assess objectives 1–4. The midterm exam tested students’ understanding of concepts stemming from the first half of the laboratories, while the final exam material was based on the second half. The majority of each exam (56% of the midterm and 75% of the final) consisted of chemistry word problems that required calculations. Partial credit was awarded if the math reasoning was structured correctly but a calculation error resulted in an incorrect final answer. The remaining questions assessed knowledge of chemical definitions, laboratory safety, laboratory notebook basics, and formal laboratory report organization.

At the first and last laboratory meetings, students completed identical 13-question, multiple-choice, math-specific assessments specifically designed to be implemented during a two-hour laboratory course (Appendix A, ESI†). They were given 15 minutes for this assessment and had access to only a calculator. Math concepts critical to the first semester of an introductory chemistry course were each represented by one to three questions. These concepts included the following: fractions, exponents, percentages, scientific notation, significant figures, basic operations, algebra, unit conversions, and graphing. The math assessment contained six fewer questions than the general mathematics portion of the American Chemical Society Toledo Placement Exam, but both assess math skills up to and including algebra. Results from this assessment were included in the weekly laboratory grade as an incentive.

Students also kept laboratory notebooks and were instructed to come to the laboratory session with the date and purpose of the experiment recorded in advance. Laboratory notebooks were checked at least three times throughout the semester to enforce consistent use and entering data in a timely fashion. At the end of the semester, laboratory notebooks were collected and graded based on those previous checks, as well as completeness of a table of contents and neatness. These notebooks assessed objectives 1–4. Assessment of laboratory technique and cleanliness were tied to learning objectives 1 and 2.

As the 4th learning objective was to “Know and be able to apply the mathematics required in chemistry and for calculation of accurate experimental results”, the critical math concepts listed above were emphasized throughout the entirety of the course, and each was assessed by at least 3 different methods.

Overall grades were calculated with the following weights: laboratory work (pre-laboratory quiz, post-laboratory worksheet of experimental data and conclusions) 60%, one formal laboratory report 10%, midterm exam 10%, final exam 10%, laboratory notebook 5%, and laboratory technique and cleanliness 5%. Statistical significance between groups was analyzed by one-tailed unpaired t tests. Differences between pre- and post-math assessments taken by the same students were calculated by one-tailed paired t-tests. All calculations were performed in Microsoft Excel.

Laboratory partner pairings

Although no instrument exists that will perfectly assess math ability, the SAT math test has been used historically as one such metric (Pickering, 1975; Ozsogomonyan and Loftus, 1979; Spencer, 1996Wagner et al., 2002; Tai et al., 2006). Consenting students’ SAT math scores (n = 122) were divided into quartiles for each section of the class. For the few instances when only the ACT was taken, the corresponding SAT math score was determined (Dorans, 1999). Within each of the five experimental sections of the course, laboratory partners were assigned so that 1st and 4th quartile scorers were partnered and 2nd and 3rd quartile scorers were partnered, whenever possible. This way, students working in each partnership differed in math skills. Additionally, this experimental design aimed to promote achievement among all students by not pairing students in the 50th percentile (1st and 2nd quartile) together. Students were unaware of the basis for these partnerships. Students in the five control sections selected their own partners. Designation of control or experimental sections was based on several criteria to minimize instructor effects and other variables. Each instructor taught one control and one experimental section each semester. Secondly, average SAT math scores were analyzed in order to prevent a combination of students with significantly different performances on this assessment (unpaired student's t-test comparing control and experimental SAT math scores resulted in p = 0.82). Partnerships remained consistent throughout the semester, with the exception of the very first laboratory, which occurred before SAT data was collected, and two later labs when partnerships combined into groups of three or four in order to facilitate instrument use. Assessment data is presented from either all students collectively (self-selected vs. assigned partnerships) or designated into “top” and “bottom” (50th percentile) math performers.

Qualitative data concerning student attitudes and self-concepts

Consenting students were given time during the laboratory to complete a short online survey at both the beginning and end of the semester (Appendix B, ESI†). It was structured very similarly to a previously published peer learning survey for heterogeneous lab groups (Miller et al., 2012). Surveys were administered and analyzed with Qualtrics software (http://www.Qualtrics.com, Provo, UT) and were kept anonymous. At the completion of each survey, students followed a link to a second survey where names were entered to confirm completion. The names were not tied to individual responses. This allowed the instructors to incentivize students with a guaranteed bonus point on the final exam for completion of both surveys. Students who chose not to participate in the study were given an alternative, equally weighted (1 bonus point) question on the final exam. When assigned partnerships were disrupted (if a student dropped the course, for example), the remaining student was re-partnered with someone else. As a consequence, assessment and final survey data from those students affected by the re-partnering were eliminated from the study whenever possible. Seventy-six and 63 students in the control sections completed the initial survey (pre-survey) and final survey (post-survey), respectively. Seventy-five and 52 students in the experimental sections completed the pre- and post-survey, respectively. These totaled 151 pre- and 115 post-surveys that were included in the analysis. There were originally 156 potential respondents consenting to the study, for an overall response rate of 74%. Students answered demographic information and self-reported prior chemistry courses that they completed in high school/secondary school. They were also asked attitudinal and self-concept questions related to chemistry, math, and laboratory skills, as well as perceptions of working with others and contributions to the partnership. Chi-square tests were performed in Microsoft Excel to calculate p-values for survey responses between groups.

Results and findings

Student demographics

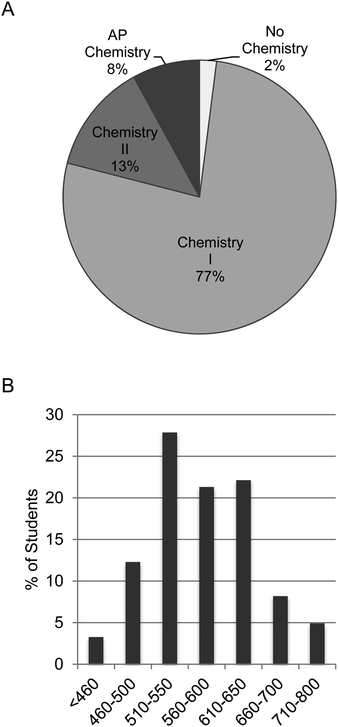
This mixed methods investigative case study was conducted in 10 sections of a first-semester introductory (also known as general) chemistry laboratory during Fall 2015 and Fall 2016. This course fulfills the laboratory science requirement within the general education curriculum and is offered every fall semester for non-chemistry and non-biochemistry majors. The majority of the students were exercise science (42%) and biology majors (31%). Pre-pharmacy majors constituted 12% of the participants, while the remaining 15% listed “other” as a major. Most students were university underclassmen; 33% were first year (freshmen), 57% were second-year (sophomores), 8% were third-year (juniors), and 2% were fourth-year (seniors). Interestingly, 75% of the students were female (Appendix C, ESI†). In terms of chemistry background, the overwhelming majority of students had completed at least chemistry I in high school/secondary school (99%). This is equivalent to standard grade chemistry or one semester of chemistry. Seventy-seven percent of students responded that chemistry I was the most advanced chemistry course completed in high school/secondary school, and 13% listed chemistry II. Approximately 8% of our students had completed Advanced Placement (AP) chemistry, which is equivalent to a first-semester university chemistry course (Fig. 1A). In terms of mathematical background, the average SAT math score was 575. These scores were obtained with Institutional Review Board (IRB) consent from the university; they were not self-reported. The distribution of these scores is shown in Fig. 1B. These background metrics were consistent between the control and experimental sections involved in the study (data not shown).

Fig. 1 Chemistry and mathematics background (A) students responded to the survey question, “What was the highest level of chemistry you completed in high school?” n = 115. AP (advanced placement), chemistry I (one semester of high school/secondary school chemistry), chemistry II (two semesters of high school/secondary school chemistry) (B) distribution of SAT math scores. n = 122.

Assigned students demonstrated larger learning gains in math concepts

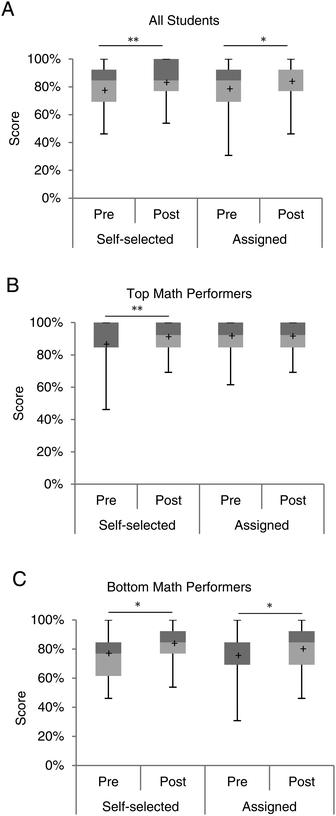
The goal of this study was to strengthen math skills; therefore, students were given the same math assessment at the beginning and at the end of the semester to help analyze learning gains in this area. The assessment was similar in concept to the general mathematics section of the Toledo Placement Exam (Table 1). This analysis revealed several important differences. Regardless of pairing, students performed significantly better at the end of the semester than the beginning (self-selected, n = 70, p = 0.003, assigned, n = 52, p = 0.04) (Fig. 2A). Both groups earned a median score of 85% on the pre-assessment (p = 0.66). Interestingly, by the end of the semester, the assigned students out-performed the self-selected students, although it was not statistically significant (p = 0.41). Assigned students demonstrated a larger learning gain, with the median math score increasing from an 85% to a 92%. Math scores of those who self-selected a laboratory partner remained the same at the end of the semester with median math scores remaining at 85%.

Table 1 Each math concept was represented on the math assessment by 1, 2, or 3 different questions. For comparison, the representation of the same math concepts is shown for the math portion of the Toledo placement exam

Math concept	Number of questions per concept
	Math assessment	Toledo placement exam
Graphing	1	2
Significant figures	2	0
Fractions & percentages	2	3
Basic mathematical operations	1	3
Algebra	3	6
Exponents	1	2
Scientific notation	1	2
Unit conversions	2	1

---

Fig. 2 Math assessment scores. In all panels, error bars represent the range of scores. Plus signs represent the means. (A) Math assessment scores earned at the beginning (pre) and end (post) of the semester. Self-selected n = 70, assigned n = 52. (B) Math assessment scores earned by the top math performers in each partnership. Self-selected n = 31, assigned n = 26. See Methods for details on quartile groupings. (C) Math assessment scores earned by the bottom math performers in each partnership. Self-selected n = 39, assigned n = 26. Statistical significance was determined using t-tests. * = p ≤ 0.05 ** = p ≤ 0.01.

Stronger math skills, as assessed by the pre- and post-assessment led us to ask if one group of students was benefiting more than another. All assessment method scores were divided into the top and bottom 50% of math performance based on SAT math scores. Consistent with previous findings (Genyea, 1983; Bohning, 1984; Russell, 1994; Donovan and Wheland, 2009), top math performers earned scores significantly higher than bottom math performers on both the pre- and post-math assessment. However, this division also revealed that top math performers significantly outperformed on the midterm, final exam, and the overall course grade, regardless of how they were partnered (Appendix D, ESI†). This further highlights that math skills are critical for a successful experience in introductory chemistry. As illustrated in Fig. 2B, top math performers generally scored above 80% on the math assessments, regardless of how they were partnered. However, bottom math performers (Fig. 2C) benefitted from a statistically significant increase in math scores. In particular, among bottom math performers who self-selected a partner, the median score on the math assessment rose from 77% to 85% (p = 0.04). Bottom math performers who were assigned to work with someone more proficient in math also demonstrated improvement from 69% to 85% (p = 0.03) (Fig. 2C). This represents a 16% improvement on the math assessment for bottom math performers in instructor-assigned pairings, while only an 8% improvement for bottom math performers in self-selected pairings. Differences in performance between groups on the pre-assessment, as well as the post-assessment were not significantly different.

Midterm and final exam outcomes were used as additional measures of math competency. We calculated scores achieved on questions covering the same chemistry-specific math concepts as the pre- and post-math assessment. Examples are given in Appendix E (ESI†). Generally, assigned students did not perform significantly better or worse than self-selected students. The only exception was the midterm exam (Appendix F, ESI†). In that case, top math performers who were assigned a lower performing partner earned a median score of 100% on math concepts, whereas “bottom” math performers earned a median score of 88% (p = 0.05).

Additional assessment methods were used to help determine if all student learning outcomes were met. These additional methods were submitted on an individual basis and all assessed a number of different math concepts (Table 2) as well as other outcomes. Median grades on the laboratory worksheets, notebooks, midterm, final exam, and the overall course grade showed no significant difference between self-selected and assigned partners (Appendix G, ESI†).

Table 2 Alignment of math concepts with assessment methods. Each math concept found on the math assessment (far right column) was represented on multiple other assessment methods

Math concept	Assessment method
	Lab notebook	Lab worksheets	Lab report	Midterm exam	Final exam	Math assessment
Graphing	×	×	×		×	×
Significant figures	×	×	×	×	×	×
Fractions & percentages	×	×		×		×
Basic mathematical operations	×	×		×	×	×
Algebra	×	×	×	×	×	×
Exponents	×	×				×
Scientific notation	×	×				×
Unit conversions	×	×		×	×	×

---

Together, these data suggest that student learning outcomes were met regardless of how students were partnered. Most median scores were the same or higher when a student was assigned to a peer with different math ability. Pairing students based on math skills did not significantly change overall grades in the course. Scores among those who were the most proficient at math did not suffer. Importantly, math assessment results indicate that bottom math performers demonstrated the largest learning gain when assigned a top math performer as a laboratory partner.

Assigned students reported a positive shift in attitude toward working with laboratory partners

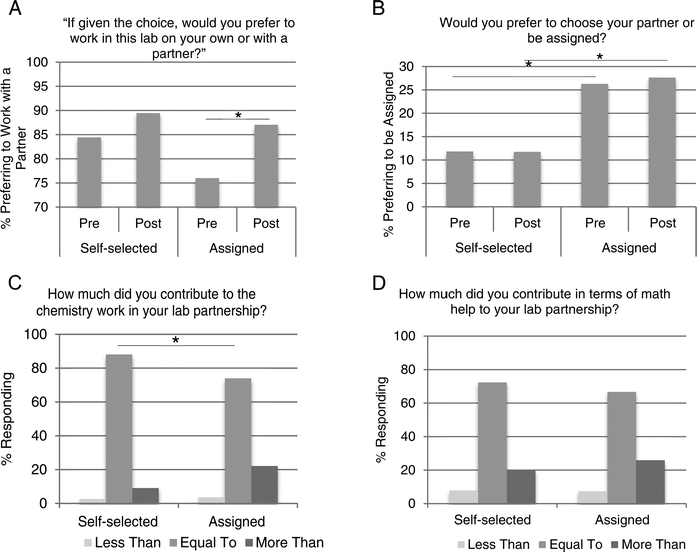
Student attitudes on a number of items were analyzed through an anonymous survey at the beginning and the end of the semester. Although all students worked with a partner, approximately half of the students were not given a choice as to whom they worked with; therefore, we wanted to gain insight into how all participants in the study viewed working collaboratively in the laboratory. Students were asked to respond to the following statement, “If given the choice, I would work with a partner.” At the beginning of the semester, 84% of self-selected students and 76% of assigned students agreed with this statement (Fig. 3A). By the end of the semester, these percentages increased in each group. Eighty-nine percent of self-selected students agreed they would prefer to work with a partner. Eighty-seven percent of assigned students responded that they would prefer to work with a partner. The change in response to this question was statistically significant (p = 0.03) only among the assigned students. If a respondent said they would prefer to work with a partner, they were then asked if they would prefer to be assigned one or choose their own. Not surprisingly, 12% of self-selected students reported that they would want to be assigned (Fig. 3B). This proportion did not change from the beginning to the end of the semester. However, at the beginning of the semester, 26% of assigned students reported that they would want to be assigned. This is significantly different from their self-selected peers' responses (p = 0.03). This percentage remained high, with 28% responding the same way at the end of the semester.

Fig. 3 Student attitudes about working with others (A) students were surveyed at the beginning (pre) and end (post) of the semester whether or not they would work with a partner or alone, if given the choice. Data shown are students responding “work with a partner.” Self-selected pre n = 90, assigned pre n = 75, self-selected post n = 76, assigned post n = 54. (B) Of those responding “work with a partner”, students were then asked if they would prefer to choose a partner or be assigned. Data shown are students responding “assigned”. Self-selected pre n = 76, assigned pre n = 57, self-selected post n = 68, assigned post n = 47 (C) students were surveyed at the end of the semester to rate their chemistry contribution to the partnership. Self-selected n = 76, assigned n = 54. (D) Students were surveyed at the end of the semester to rate their math contribution to the partnership. Self-selected n = 76, assigned n = 54. Chi-square tests were conducted to calculate p values. * = p ≤ 0.05.

In these heterogeneous populations, there is a concern that a lower-achieving student will fail to fully engage in the activities or learn from the higher-achieving student (Dembo and McAuliffe, 1987; King, 1993; Cohen, 1994). When asked to rate their contribution to the partnership in terms of chemistry concepts, 88% of students who self-selected a partner responded that it was equal to their partner's, while 74% of students in assigned partnerships said it was equal (Fig. 3C). This statistically significant difference (p = 0.04) between groups was not evident when students were asked about math contribution. Among self-selected students, 72% responded that there was an equal contribution in terms of math help. Among assigned students, this percentage was 67% (Fig. 3D).

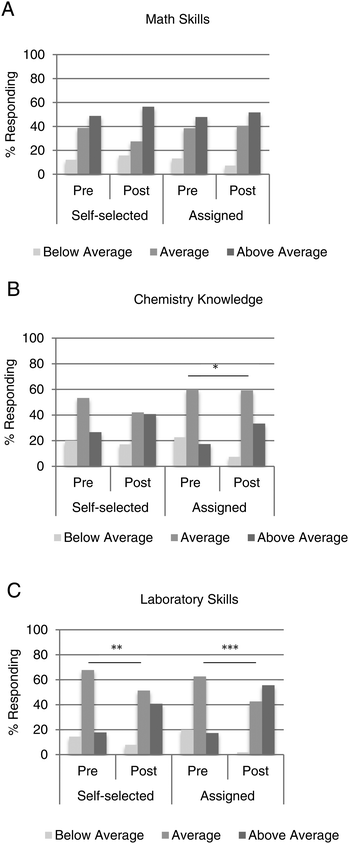
Students’ self-concepts of math skills did not change, but chemistry knowledge and laboratory skills did

We also asked students to rate their self-perceived knowledge and skill in a series of areas at the beginning and end of the course. In particular, we were interested in math skills, chemistry knowledge, and chemistry laboratory skills. In terms of math skills, students who participated in assigned partnerships had the same perception as students in self-selected partnerships, and this view remained the same at the end of the semester (Fig. 4A). Chemistry knowledge was not significantly different between the self-selected and the assigned students when polled at the start of the semester or the end (Fig. 4B). When comparing responses in the pre- and post-survey, only students in assigned partnerships reported a statistically significant shift (p = 0.02) toward above average chemistry knowledge. Perception of laboratory skills was also very similar between the two groups of students at the beginning and end of the course (Fig. 4C). Of note, however, each group of students reported a statistically significant shift toward above average laboratory skills by the end of the semester. Students partnered by varied math ability had a dramatic shift in perception of laboratory skills from 17% rating themselves as having above average skills to 56% by the end of the semester (p < 0.001). Students who chose a laboratory partner responded somewhat less favorably (p < 0.01), although with more confidence then when they started the course.

Fig. 4 Student self-concepts. Students were asked at the beginning (pre) and end (post) of the semester to rate the following: (A) math skills (B) chemistry knowledge and (C) chemistry laboratory skills. In all panels, self-selected pre n = 90, assigned pre n = 75, self-selected post n = 76, assigned post n = 54. Chi-square tests were conducted to calculate p values. * = p ≤ 0.05, ** = p ≤ 0.01, *** = p ≤ 0.001.

Discussion and limitations

Pairing lower with higher math performers in the introductory chemistry laboratory resulted in several key results. First, methods which assessed all student learning outcomes in the course (i.e. laboratory notebook, midterm, and final exam) showed no difference in median scores when partners were assigned rather than self-selected. However, when specifically assessing math skills used in introductory chemistry using the pre- and post-math assessment, assigned students showed the largest improvement (Fig. 2). Individuals in these sections earned a greater range of scores on the pre-math assessment and started with a lower median score, yet their learning gains were higher. The largest increase in math assessment score was from bottom math performers assigned to a top math performer. Although these data may support improvements in math skills, statistically, there was no difference in performance between groups.

Scores on midterm and final exams were also used to assess math performance, but assigned students had nearly the same outcomes as self-selected students (Appendix F, ESI†). One possible explanation for this disconnect with the pre- and post-math assessment findings is that these exams contained math concepts in the context of a chemical word problem. This is quite different from the math assessment that was of multiple-choice format lacking any chemistry context. Therefore, while students may be strengthening the math skills necessary to do well in chemistry, they are not yet adept at applying those skills. Since the majority of students enrolled in the laboratories were first and second year university students, they may not have had enough opportunity to practice high levels of Bloom's taxonomy such as synthesis and analysis within this context and are also still adjusting to the demands of university coursework. Students may also view the word problems on midterm and final exams as something they are relatively uncomfortable with, compared to a more familiar multiple choice math assessment, as they would have encountered in high school and on entrance exams. It would be worthwhile to follow students in this study through the second semester of introductory chemistry to determine if math performance continues to improve and if additional practice with solving chemistry word problems results in higher performance on more in-depth assessment methods.

Overall, math performance was not negatively affected by this study. In fact, many positive changes were observed that enhanced the chemistry lab experience. These attitudinal and self-concept findings were the most striking and gave us valuable insight into the dynamics of a laboratory partnership. Importantly, students who were assigned a partner showed a statistically significant positive shift in attitude toward working with partners, while those who chose a partner did not (Fig. 3A). The majority of students in both groups perceived that there was an equal contribution by each member of the team (Fig. 3C and D). This is worth noting because there are valid concerns about self-perceived differences in skills when working with heterogeneous peer groups (Dembo and McAuliffe, 1987; King, 1993; Gabriele and Montecinos, 2001). Although a slight disparity in chemistry contribution to the partnership was detected among students who had an assigned laboratory partner, differences in math contributions were not reported (Fig. 3C and D). This was somewhat surprising, as math skill was used in creating the heterogeneous peer groups, although we did not share with students the basis for these partnerships. These particular survey results were collected at the completion of the course, so it may be that the initial heterogeneous partnerships were perceived as more homogenous in terms of math by the end of the semester. An alternative explanation is that students considered both math and chemistry contributions when answering the survey question targeting chemistry contribution alone.

We encountered very few partnerships that did not work effectively. Only one student requested a partner change mid-semester because the other student was not contributing equally. After discussing the situation, this may have been due to differences in maturity. This student was a second year (sophomore) working with a first year (freshman). We suggested some techniques consistent with those in Cohen et al. (Cohen, 2004), such as focusing on individual strengths that each person can bring to the partnership. Although one student might struggle with calculations on the laboratory worksheet, that same individual might be more skilled at time management or operating a particular instrument. Regardless, this data revealed that the majority of students felt that there was an equal contribution to the coursework. Assigning partners did not create a scenario where one student was heavily relying on the other to complete the experiments and related work. This was consistent with our previous study in a biotechnology laboratory course (Miller et al., 2012) and supports the idea that enhanced perceptions of working with others can be a result of heterogeneous peer groups, even when group formation is based on different criteria. Furthermore, it demonstrates that this practice has the potential to be effective in a variety of courses.

In the sections of our study that had no choice in partner, the percentage of students who responded that they would prefer to be assigned was significantly higher than those who were choosing their own partner. Interestingly, this difference in attitude was in place even at the beginning of the semester (Fig. 3B). We hypothesize that since the students were already told if they were choosing or being assigned a partner, they responded to the survey question in a way that reflected their current situation. That is, if the instructor told them they will be assigned a lab partner, they were much more likely to be in favor of that. This trend was observed in both semesters of data collection and suggests that notifying students of this peer learning structure influences their response.

As expected, students’ self-concepts in terms of math skills showed a positive shift by the end of the semester, but this was observed with students who self-selected a partner as well as those who were assigned (Fig. 4A). These survey responses were very similar to those obtained by Johnston et al. (Johnston et al., 2016). It was somewhat surprising that some students did not readjust their own awareness of mathematical performance after working one-on-one with a peer of dissimilar performance. One possibility is that by analyzing the perceptions of all responders, we are missing potential differences between top and bottom math achievers. It is likely that different subsets of students would have unique viewpoints on peer learning-related questions, however, breaking down the responses by level of math performance would result in numbers too small to apply statistical significance.

Not surprisingly, 53% of self-selected students and 60% of assigned students reported “average” chemistry knowledge at the beginning of the semester (Fig. 4B). But, only assigned students had significantly higher self-concepts by the end of the semester. Furthermore, both groups had significantly higher self-concepts in chemistry laboratory skills, with the assigned students reporting the most significant difference (Fig. 4C). These findings are in support of peer learning promoting self-concepts in both chemistry knowledge and laboratory skills, similar to findings stemming from a linguistics course (Duran Gisbert and Monereo Font, 2008). These changes in self-perception over time are most likely influenced not just by the peer learning environment, but also by many factors. The laboratory and lecture courses would influence this viewpoint, as well as experiences outside of these meetings. Students who completed the course with a partner of dissimilar math ability may have experienced a gain in confidence, regardless if they were the stronger or weaker partner.

Although this work took place in a laboratory environment, it is worth restating that the lecture component was a separate course. We did not analyze student learning in the context of the lecture course, as the laboratory was a separately graded course. Therefore, most students had different lecture and laboratory instructors. The individuals involved in this study were only a subset of the lecture instructors. Furthermore, peer groups were not utilized in the lecture sections. However, no instructor utilized a radically different pedagogical technique, and the same textbook, online homework system, and laboratory materials were in place.

The math assessment was designed to be administered at the beginning of a two-hour laboratory, and therefore each math concept was only represented by 1 to 3 items, which could be considered limited in depth. Therefore, in an effort to be more comprehensive, the midterm and final exams were also analyzed to help measure math competency. An additional limitation of this study was that we were unable to filter assessment method scores into each quartile of math performance. Quartiles were based on SAT math scores and were defined in each individual section of the class. Therefore, quartiles were only representative of a student's particular lab section, not the entire study population. For instance, an SAT math score of 540 may have fallen in the limits of the 1st quartile in one section of the class, but the 2nd quartile in another. For this reason, the 1st and 2nd quartiles were combined to represent bottom math performers, and the 3rd and 4th quartiles constituted the top math performers.

Recommendations for practice

Peer learning occurs in most chemistry laboratory courses. Practical advantages of partners in a chemistry laboratory course are numerous. For one, instructors often consider this a safer alternative to individual work. This arrangement also greatly decreases the overall amount of reagents necessary, saves money, decreases preparation time, and facilitates instrumentation use. Therefore, if most instructors already have students working together, they can easily implement peer learning to maximize the benefits in these partnerships. In our experience, benefits from assigning partners greatly outweigh any negative feedback. Aside from mathematics, other differences in particular skills can be used to create heterogeneous peer groups. The methods presented here could also be adopted by courses other than introductory chemistry laboratories. However, in order to address weaknesses in math skills, we chose a foundational chemistry course as the most appropriate setting to promote further improvement. Additionally, if students experience working with others that have abilities different than their own in introductory courses, they may be more receptive to this arrangement in subsequent courses in their curriculum. Future longitudinal studies that follow these students could be performed to address that hypothesis. Our work demonstrates that student attitudes toward working with others are improved by this simple intervention. Ultimately, these peer learning experiences may help promote not just mathematical and chemical skills, but lifelong learning skills (Boud et al., 2006).

Finally, these positive shifts in perception, especially among weaker math students, suggests that students are open to intellectual growth in a topic they find challenging. We are currently implementing growth mindset interventions that may further enhance student perceptions and performance in math and chemistry.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to thank all members of the High Point University Chemistry Department for their input in this project. In particular, Dr. Todd Knippenberg and Dr. Pam Knippenberg were crucial in helping collect data from their sections of the course. H. B. M. would also like to acknowledge Dr. Angela Bauer and the High Point University Teaching Scholars for supporting this endeavor.

References

1. Bauer C. F., (2005), Beyond “Student Attitudes”: Chemistry Self-Concept Inventory for Assessment of the Affective Component of Student Learning, J. Chem. Educ., 82, 1864 DOI:10.1021/ed082p1864.
2. Beane J. A. and Lipka R. P., (1986), Self-Concept, Self-Esteem, and the Curriculum, New York: Teachers College Press.
3. Berger J., Zelditch M. and Anderson B., (1966), Sociological theories in progress, Boston: Houghton Mifflin.
4. Bohning J. J., (1984), Remedial mathematics for the introductory chemistry course: the “CHEM. 99” concept, J. Chem. Educ., 59, 207.
5. Bossert S. T., (1988), Cooperative Activities in the Classroom, Rev. Res. Educ., 15, 225–250.
6. Boud D., Cohen R. and Sampson J., (2006), Peer Learning and Assessment, Assessment & Evaluation in Higher Education, 24, 413–426 DOI:10.1080/0260293990240405.
7. Carr J. M., (2013), Using a Collaborative Critiquing Technique To Develop Chemistry Students’ Technical Writing Skills, J. Chem. Educ., 90, 751–754 DOI:10.1021/ed2007982.
8. Chambers K. A. and Blake B., (2007), Prediciting student succes in general chemistry: a multivariate approach. The American Chemical Society CHED-219.
9. Cohen E. G., (1982), Expectation States and Interracial Interaction in School Settings, Annu. Rev. Social., 8, 209–235.
10. Cohen E. G., (1994), Restructuring the Classroom: Conditions for Productive Small Groups, Rev. Educ. Res., 64, 1–35.
11. Cohen E. G., (2004), Designing groupwork: strategies for the heterogeneous classroom, New York: Teachers College Press.
12. Cohen E. G. and Lotan R. A., (1995), Producing Equal-Status Interaction in the Heterogeneous Classroom, Am. Educ. Res. J., 32, 99–120.
13. Cohen E. G. and Lotan, R. A., (1997), Working for equity in heterogeneous classrooms: sociological theory in practice, New York: Teachers College Press.
14. Collegeboard, (2017), Class of 2017 SAT Results [Online]. CollegeBoard, available: http://https://reports.collegeboard.org/sat-suite-program-results/class-2017-results, accessed 10/17/17.
15. Davidson N., (1990), Cooperative learning in mathematics: a handbook for teachers, Menlo Park, Calif: Addison-Wesley Pub. Co.
16. Dembo M. H. and McAuliffe T. J., (1987), Effects of Perceived Ability and Grade Status on Social Interaction and Influence in Cooperative Groups, J. Educ. Psychol., 79, 415.
17. Ding N. and Harskamp E. G., (2011), Collaboration and Peer Tutoring in Chemistry Laboratory Education, Int. J. Sci. Educ., 33, 839–863 DOI:10.1080/09500693.2010.498842.
18. Donovan W. and Wheland E., (2009), Comparisons of success and retention in a general chemistry course before and after the adoption of a mathematics prerequisite, Sch. Sci. Math., 109, 371.
19. Dorans N. J., (1999), Correspondances between ACT and SAT I Scores, The College Board.
20. Duran Gisbert D. and Monereo Font C., (2008), The Impact of Peer Tutoring on the Improvement of Linguistic Competence, Self-Concept as a Writer and Pedagogical Satisfaction, Sch. Psychol. Int., 29, 481–499 DOI:10.1177/0143034308096437.
21. Esmonde I., (2009), Ideas and Identities: Supporting Equity in Cooperative Mathematics Learning, Rev. Educ. Res., 79, 1008–1043.
22. Fuchs D., Fuchs L. S., Mathes P. G. and Simmons D. C., (1997), Peer-Assisted Learning Strategies: Making Classrooms More Responsive to Diversity, Am. Educ. Res. J., 34, 174–206.
23. Fuchs L. S., Fuchs D., Hamlett C. L. and Karns K., (1998), High-Achieving Students' Interactions and Performance on Complex Mathematical Tasks as a Function of Homogeneous and Heterogeneous Pairings, Am. Educ. Res. J., 35, 227–267.
24. Gabriele A. J. and Montecinos C., (2001), Collaborating With a Skilled Peer: The Influence of Achievement Goals and Perceptions of Partners' Competence on the Participation and Learning of Low-Achieving Students, The Journal of Experimental Education, 69, 152–178 DOI:10.1080/00220970109600654.
25. Genyea J., (1983), Improving students' problem-solving skills, J. Chem. Educ., 60, 478–482.
26. Hodgen J., Pepper D., Sturman L. and Ruddock G., (2010), An international comparison of upper secondary mathematics education, London.
27. Hooker D., (2011), Small Peer-Led Collaborative Learning Groups in Developmental Math Classes at a Tribal Community College, Multicultural Perspectives, 13, 220–226 DOI:10.1080/15210960.2011.616841.
28. Hovey N. W. and Krohn A., (1958), Predicting failures in general chemistry, J. Chem. Educ., 35, 507.
29. Hovey N. W. and Krohn A., (1963), An evaluation of the Toledo chemistry placement examination, J. Chem. Educ., 40, 370.
30. Johnson D. W., Maruyama G., Johnson R., Nelson D. and Skon L., (1981), Effects of Cooperative, Competitive, and Individualistic Goal Structures on Achievement: A Meta-Analysis, Psychol. Bull., 89, 47–62.
31. Johnston P. R., Watters D. J., Brown C. L. and Loughlin W. A., (2016), An investigation into student perceptions towards mathematics and their performance in first year chemistry: introduction of online maths skills support, Chem. Educ. Res. Pract., 17, 1203–1214.
32. King L. H., (1993), High and Low Achievers' Perceptions and Cooperative Learning in Two Small Groups, Elem. Sch. J., 93, 399–416.
33. Kramarski B. and Mevarech Z. R., (2003), Enhancing Mathematical Reasoning in the Classroom: The Effects of Cooperative Learning and Metacognitive Training, Am. Educ. Res. J., 40, 281–283 DOI:10.10.3102/00028312040001281.
34. Larson C. O., Dansereau D. F., O'donnell A., Hythecker V., Lambiotte J. G. and Rocklin T. R., (1984), Verbal Ability and Cooperative Learning: Transfer of Effects, J. Lit. Res., 16, 289–295 DOI:10.1080/10862968409547522.
35. Marsh H. W. W. and Debus R., (1991), Contemp. Educ. Psychol., 16, 331–345.
36. McCreary C. L., Golde M. F. and Koeske R., (2006), Peer Instruction in the General Chemistry Laboratory: Assessment of Student Learning, J. Chem. Educ., 83, 804–810.
37. Miller H. B., Witherow D. S. and Carson S., (2012), Student learning outcomes and attitudes when biotechnology lab partners are of different academic levels, CBE Life. Sci. Educ., 11, 323–332 DOI:10.1187/cbe.11-10-0094.
38. Ozsogomonyan A. and Loftus D., (1979), Predictors of general chemistry grades, J. Chem. Educ.56, 173 DOI:10.1021/ed056p173.
39. Pickering M., (1975), Helping the high risk freshman chemist, J. Chem. Educ., 52, 512 DOI:10.1021/ed052p512.
40. Popejoy K. and Asala K. S., (2013), A team approach to successful learning: peer learning coaches in chemistry, J. Coll. Sci. Teach., 42, 18.
41. Rowe M. B., (1983), Getting chemistry off the killer course list, J. Chem. Educ., 60, 954 DOI:10.1021/ed060p954.
42. Russell A. A., (1994), A rationally designed general chemistry diagnostic test, J. Chem. Educ., 71, 314–317.
43. Shibley I. A. and Zimmaro D. M., (2002), The Influence of Collaborative Learning on Student Attitudes and Performance in an Introductory Chemistry Laboratory, J. Chem. Educ., 79, 745 DOI:10.1021/ed079p745.
44. Slavin R. E., (1983), When does cooperative learning increase student achievement? Psychol. Bull., 94, 429–445.
45. Spencer H. E., (1996), Mathematical SAT Test Scores and College Chemistry Grades, J. Chem. Educ., 73, 1150 DOI:10.1021/ed073p1150.
46. Srougi M. C., Miller H. B., Witherow D. S. and Carson S., (2013), Assessment of a novel group-centered testing schema in an upper-level undergraduate molecular biotechnology course, Biochem. Mol. Biol. Educ., 41, 232–241 DOI:10.1002/bmb.20701.
47. Tai R. H., Ward R. B. and Sadler P. M., (2006), High school chemistry content background of introductory college chemistry students and its association with college chemistry grades., J. Chem. Educ., 83, 1703–1711.
48. Wagner E. P., Sasser H. and Dibiase W. J., (2002), Predicting Students at Risk in General Chemistry Using Pre-semester Assessments and Demographic Information, J. Chem. Educ., 79, 749 DOI:10.1021/ed079p749.

---

Footnote

† Electronic supplementary information (ESI) available: The math assessment, additional assessment method results, anonymous surveys, and additional student demographic data obtained from the surveys. See DOI: 10.1039/c7rp00152e

---