Using a multi-tier diagnostic test to explore the nature of students’ alternative conceptions on reaction kinetics
Yaw Kai
Yan
 and
R.
Subramaniam
and
R.
Subramaniam
 *
*
National Institute of Education, Nanyang Technological University, 1 Nanyang Walk, Singapore 637616. E-mail: subramaniam.r@nie.edu.sg
First published on 15th November 2017
Abstract
This study focused on grade 12 students’ understanding of reaction kinetics. A 4-tier diagnostic instrument was developed for this purpose and administered to 137 students in the main study. Findings showed that reaction kinetics is a difficult topic for these students, with a total of 25 alternative conceptions (ACs) being uncovered. Except for one AC, the other ACs uncovered have not been reported before in the literature. An interesting point emerging from this study is that nearly 70% of the ACs were obtained from questions that featured graphs. Overall, the 4-tier format for the diagnostic instrument demonstrates good utility for probing students’ understanding of reaction kinetics as well as uncovering their ACs. The confidence-related measures, which are more commonly used in the educational psychology literature, have also permitted further insights to be gained into how the students performed in the test as well as the classification of the ACs.
Introduction
Studies on students’ understanding of various topics in the sciences have been an important aspect of research in science education. Such studies have provided a wealth of knowledge on misconceptions and learning difficulties harbored by students on a topic, and these can be leveraged by instructors during lesson delivery. Misconceptions and learning difficulties are stumbling blocks for students to attain a holistic understanding of a topic and, if these can be identified and addressed through suitable conceptual change strategies, gaps in the students’ conceptual framework can be better bridged.Students do not come to the class with absolutely no knowledge of a topic. Their experiences in the natural world have imbued them with certain ideas about science, knowingly or unknowingly, that they bring to the classroom. When content that is taught finds some resonance with what they already know, such concepts can be assimilated into their conceptual schemata to varying extents. This is, of course, the basis of constructivism (Kalina and Powell, 2009). In other words, students’ minds are not empty slates on which knowledge can be imprinted. Content that is presented by the instructor does not equate to knowledge in students if this is not internalized within them in a meaningful manner. If they are not able to make sense of these, then rote learning can be resorted to (Ausubel et al., 1978, p. 117; Klassen, 2006). Besides students’ experiences in the natural world, their prior knowledge on a topic can also affect the extent to which they can understand aspects of the topic. For example, in the study of chemical bonding, students need to invoke what they have previously learnt about atomic structure, especially the presence of electrons in the outermost orbital, before they can appreciate ionic or covalent bonding. More importantly, the presence of misconceptions can interfere with the learning process – the literature on misconceptions is clear in that the discrete elements that constitute a concept and that are supposed to be interconnected in the mental framework of a student can exhibit discontinuities if knowledge acquisition is fragmented or less than optimal (for example, Taber, 2000; den Broek, 2010).
Students’ ideas about many concepts in the sciences are often at odds with what scientists consider to be canonical knowledge. This variation in their understanding with respect to the scientific norm has been imbued with a variety of labels – for example, misconceptions (Amir and Tamir, 1994), alternative conceptions (ACs) (Wandersee et al., 1993), and alternative frameworks (Gilbert and Watts, 1983). Irrespective of the label affixed, these are perceived to be impediments to attaining conceptual understanding. If these can be identified and addressed, students’ conceptual understanding of a topic can be further enhanced. Approaches to identify misconceptions are thus important, and these have helped in documenting numerous misconceptions in the sciences. An extensive bibliography of over 8400 references on misconceptions and learning difficulties in the sciences is available (Duit, 2009).
Some of the common approaches to identify misconceptions include the use of open-ended questions (Reynolds et al., 2006), multiple choice questions (Tekin and Nakiboglu, 2006), two-tier questions (Lin, 2004), and interviews (Voska and Heikkinen, 2000).
Properly set open-ended questions have tremendous value in diagnosing misconceptions for the simple reason that they force students to draw on their explanatory framework to demonstrate their understanding. Gaps in their understanding can then be detected and, if these recur across a sample with modest regularity, these can be considered as ACs. However, the downside of using open-ended questions is that marking can be time-consuming, and identifying ACs can be problematic since it would entail coming up with coding schemes to interpret the diversity of responses.
Multiple choice questions can also be used to identify ACs. This format is popular with teachers for assessment purposes as marking is easier – in fact, with machine-based marking, teachers need not even mark these questions. Where incorrect responses occur at a frequency above the chance selection level (usually 10% and above), these distracters can be considered as ACs.
The two-tier format has been the basis of numerous studies in identifying ACs in the sciences. In the most common version used, both the answer and reason tiers are in the MCQ format. Besides two-tier MCQs, other variants of multi-tier diagnostic instruments include the 3-tier (Caleon and Subramaniam, 2010a) and 4-tier (Caleon and Subramaniam, 2010b) formats. The latter two formats are of more recent origins. The 3-tier format is basically a 2-tier format but with a mean confidence scale for students to indicate how confident they are in the correctness of their responses to the answer and reason tiers. The 4-tier format also essentially mirrors the two-tier format but with a separate confidence scale for each of the two tiers for students to indicate how confident they are in the correctness of their responses in the answer and reason tiers respectively. The addition of a confidence scale helps to overcome some of the limitations of the two-tier format. In the 2-tier format, it is not easy to differentiate whether a correct response represents good understanding or whether it is due to guesswork (Caleon and Subramaniam, 2010a). Also, for incorrect responses, it is not easy to determine whether these are due to a lack of knowledge or to ACs. The inclusion of the confidence scale addresses these limitations to some extent. For example, if the response is incorrect but the confidence is low, then it could indicate a lack of knowledge rather than the presence of an AC. Likewise, if the response is correct but the confidence is low, it could mean a lack of knowledge rather than good understanding. Studies on 3-tier and 4-tier instruments are rather few. With respect to the former, we can cite studies such as those by Caleon and Subramaniam (2010a), Arslan et al. (2012), Peşman and Eryılmaz (2010), and Yan and Subramaniam (2016). With respect to the 4-tier format, we can cite the following works: Caleon and Subramaniam (2010b); Sreenivasulu and Subramaniam (2013, 2014) and McClary and Bretz (2012). Clearly, there is a need for more work to appraise the efficacy of these instruments with different topics.
For this study, we opted for the 4-tier format rather than a 3-tier version. There are two reasons for this. First, as each tier tests for different aspects of the concept in question, students are likely to have different levels of confidence for each tier. Indeed, they often have different levels of confidence for both tiers, as can be seen from the foregoing studies on the 4-tier formats. Thus, it makes sense to have a confidence scale for each tier. Second, if students are asked to provide a mean confidence rating for both tiers, it may not be totally accurate if they have different levels of certainty for the veracity of their responses for each tier.
By its very nature, a diagnostic instrument can cover only limited aspects of a topic. There are a few reasons for this. A very comprehensive diagnostic instrument on a topic can be overwhelming for students to complete due to the large number of questions involved and the time taken to complete it. Also, compared to traditional MCQs, the cognitive processing needed to complete a diagnostic instrument, for example, a two-tier test, is greater and this is further exacerbated by the difficulty level of the distracters since these are common ACs. Moreover, as diagnostic instruments are basically used by researchers to study the nature of students’ understanding of a topic and is a low-scoring test, dependence on the goodwill of schools for the study is also needed, and this is more likely with a short diagnostic instrument. The literature is replete with the diversity of diagnostic instruments on a single topic – for example, on waves (Caleon and Subramaniam, 2010a, 2010b); electrochemistry (Lee, 2007; Sia et al., 2012); and diffusion and osmosis (Odom, 1995; Odom and Barrow, 1995). Likewise, the present study focuses on selected aspects of the chemistry topic of reaction kinetics.
Students' alternative conceptions on reaction kinetics
An excellent review of educational studies on reaction kinetics has recently appeared in this journal (Bain and Towns, 2016), and this is a follow-up on an earlier review by Justi (2003). It can be noted that reaction kinetics has been the subject of a number of studies, especially at secondary and university levels. One feature of the review by Bain and Towns is the documenting of common ACs on reaction kinetics. However, the number of ACs identified on this topic at the upper high school level (grades 11–12), as reported in this review, is rather limited, considering that the topic has considerable breadth and scope. Also, most of the ACs documented in the literature at various levels can generally be regarded as those pertaining to common concepts – for example, when temperature is increased, time taken for a reaction to occur increases; endothermic reactions occur more slowly than exothermic reactions; and so on.Table 1 summarizes some of the common ACs on reaction kinetics reported in the literature and that are applicable for grades 11–12. A number of these ACs are from references related to work conducted in higher education settings (Çakmakci, 2010) and with teachers (Kolomuç and Tekin, 2011). It is clear that difficulties in fundamental concepts related to reaction kinetics persist in students even after the high school level.
| Alternative conception | Ref. |
|---|---|
| Reaction rate is the time required for reactants to form products. | Akkus et al. (2003) |
| Reaction rate is equal to the product of concentrations of reactants. | Kolomuç and Tekin (2011) |
| Increasing the concentration of reactants increases the reaction time. | Kurt and Ayas (2012) |
| When the temperature is increased, the rate of the endothermic reaction increases, but the rate of the exothermic reaction decreases. | Hackling and Garnett (1985) |
| Increasing temperature increases the time necessary for a reaction to occur. | Kırık and Boz (2012) |
| Exothermic reactions occur faster than endothermic reactions (and vice versa). | Çakmakci (2010) |
| Increasing the temperature of exothermic reactions increases the rate of the forward reaction. | Yalçınkaya et al. (2012) |
| Increasing the temperature increases the activation energy. | Yalçınkaya et al. (2012) |
| As temperature decreases the activation energy, it enables the reaction to increase its rate. | Kolomuç and Tekin (2011) |
| The catalyst increases the average speed of the molecules. | Kurt and Ayas (2012) |
| Catalyst increases reaction rate by decreasing the kinetic energy of the molecules. | Yalçınkaya et al. (2012) |
| A catalyst does not react with any of the reactants or products. | Yalçınkaya et al. (2012) |
| Reaction rate increases as the reaction progresses. | Hackling and Garnett (1985) |
It is also essential to derive ACs from more difficult contexts, especially from questions testing multiple concepts within the same domain, and this would be one of the objectives of the present study.
Moreover, it can be noted from the literature that there is a paucity of studies in uncovering ACs on reaction kinetics among upper high school students through the use of diagnostic instruments. Supasorn and Promarak (2015) used a 2-tier instrument to assess the efficacy of instruction using inquiry and analogies among grade 11 students. The nature of their instrument is more conceptual rather than diagnostic, and since it is set in the Thai language, there is also the issue of its wider use in countries where the English language is used for teaching. Seçken and Seyhan (2015) recently studied the links between academic achievement and anxiety among grade 11 students when they do problems on the rate of reaction set in graphical contexts; however, no ACs were documented in their study. A more recent study by Yan and Subramaniam (2016) explored students’ understanding of reaction kinetics among grade 12 students using a 3-tier diagnostic instrument and documented 23 ACs on certain aspects of reaction kinetics. We also note that a 4-tier diagnostic instrument on reaction kinetics is not available in the literature.
It needs no reiterating that diagnostic instruments available on various topics can encourage teachers to use these to identify ACs among their students, thus giving them valuable pointers for enhancing the effectiveness of their own teaching. In fact, Morrison and Lederman (2000) opined that a key reason why teachers do not use diagnostic instruments to identify ACs among their students is the non-availability of such instruments. It has to be recognized that given the depth and breadth of content in a topic, any diagnostic instrument can only survey selected aspects of the topic since it commonly comprises a limited number of questions. It will be overwhelming for students to sit for a very comprehensive diagnostic instrument on a topic – the sheer length of such an instrument and the time needed to take the test can induce fatigue among students and this has implications for test validity and reliability. Likewise, the present study focuses on selected aspects of ACs related to reaction kinetics. Another reason for our focus on the grade 12 level is that it represents a key stage before students go on to university and, if they decide to study chemistry, there is a possibility of carry-over of some of their ACs on reaction kinetics when they study this topic later in greater depth. With knowledge of the common ACs, teachers can pay more attention to concepts leading to the ACs so that the latter do not emerge in the first place in students as well as use conceptual change strategies to address the more tenacious ACs. It is a common practice for teachers to cover only content prescribed by the syllabus, with little attention paid to ACs.
In summary, the rationale for embarking on this study can be summarized as follows:
(a) to contribute to educational studies on reaction kinetics at the grade 12 level where there are a limited number of references as well as ACs documented;
(b) to develop a 4-tier diagnostic test on reaction kinetics so that ACs can be identified more robustly on the basis of not only selection frequency but also in tandem with confidence measures; and
(c) to continue the conversation on the 4-tier diagnostic format in the literature for uncovering ACs and where there are only a handful of studies in the science education literature.
Keeping in mind the gaps in the literature, the following research questions underpinned our study:
1. What ACs on reaction kinetics do grade 12 students have?
2. What do the confidence measures indicate with respect to students’ understanding of the domain tested as well as the alternative conceptions found?
3. What is the efficacy of the 4-tier format in identifying ACs?
Methodology
Development of a diagnostic instrument on reaction kinetics
This basically parallels the approach described by Treagust (1986, 1988) for 2-tier instruments but with some slight variations. The content perimeters of the topic were demarcated by consulting the syllabus for Grade 12 Chemistry. The journal literature, past year examination questions, assessment books, and authors’ teaching experiences were leveraged in framing 15 questions for the preliminary version of the instrument in the 2-tier version – the answer tier in the MCQ format and the reason tier in the open-ended formant.We did not use interviews to probe students’ understanding with a view towards uncovering further ACs. While interviews would be helpful in probing the nuances of students’ understanding, it is time-consuming. Instead, the authors leveraged their teaching experiences also in coming up with the preliminary version of the instrument. The first author has taught reaction kinetics, among other topics, to undergraduates and over the course of his interactions with several classes of students over the years, is familiar with some of the common learning difficulties and ACs on reaction kinetics that students bring over from high school. The second author has taught pre-service teachers who later go on to teach high school Chemistry at the grade 11–12 level, and is also conversant with some of the common learning difficulties and ACs in the course of his interactions with them. It has also to be reiterated that interviews of a few students can only uncover ACs among this particular group and it is not easy to extrapolate these across a cohort. More importantly, the learning difficulties and ACs on reaction kinetics that the authors have become familiar with were culled from a number of cohorts of students and can thus be argued to have more generalizability than the interview responses of a few students. In fact, even the recent studies reported by Sreenivasulu and Subramaniam (2013, 2014) using 4-tier diagnostic tests on university students did not use interviews. There is thus also a need for studies that do not use interviews so that the conversation on development of diagnostic instruments can be continued further in this context in the literature.
The preliminary version of the instrument was administered to a sample of grade 12 students (N = 96). Based on the responses of the students in the reason tier, the next version of the instrument was prepared, with the reason tier also in the MCQ format. Four questions from the preliminary version of the instrument were not used as students had little difficulty in answering these questions.
The MCQ options in the reason tier for each question comprise one correct reason plus 3–4 incorrect reasons. With respect to the latter, we selected the most commonly occurring faulty reasoning in the open-ended responses corresponding to each distracter. Where necessary, we polished up the responses so that these are grammatically correct and flow well. Also, where students’ responses were not clear or lacking, the authors used their own teaching experience to craft the distracters. This version of the instrument was sent to two academics for validation. With respect to the latter, we sent a covering letter to the academics explaining the purpose of our study and what was required of them. They were given a checklist to help them in their task. The checklist contained the following items that they needed to tick with either a yes or no: the questions are related to the topic of reaction kinetics in the syllabus at the junior college level; the questions, answers and reasons are free of grammatical errors; the questions in the diagnostic instrument are clear and comprehensible; the particular format used in the diagnostic instrument is effective in probing the students’ understanding of the topic; the correct responses indicated in the answer and reason tiers are acceptable; each tier has only one correct response, with the rest being misconceptions; overall, the diagnostic instrument can provide useful information for the research study; and the one hour allocated for students to complete the instrument is adequate. In addition, next to each item, there was a space for them to provide comments. The validators were basically in agreement with the instrument developed and suggested some slight changes, which were incorporated. Confidence scales were then added for both tiers – this ranged from Just guessing (1) to Absolutely confident (6), and were deemed adequate for the purpose of our study.
For the instrument, we did not include a blank response for each tier. This would have allowed students to provide their own written responses if they disagreed with any of the responses found in the answer/reason tiers. There are two reasons for this – firstly, we felt that the given responses were adequate; and secondly, we thought that if a blank option was provided, it might be minimally used. In fact, in the preliminary study conducted, we found that quite a number of students had difficulties in providing a response for the open-ended reason tier. Further support for our stance is found in the recent studies by Sreenivasulu and Subramaniam (2013, 2014), who did not include a blank option, and that was for university students.
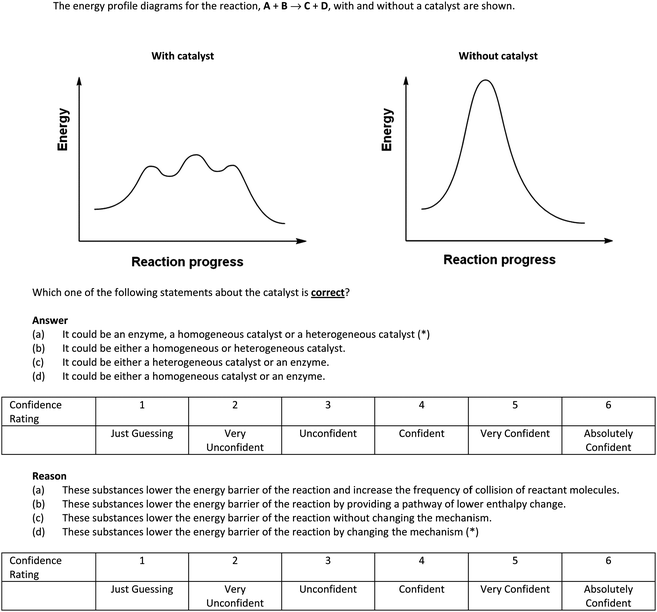
A sample question appears in Fig. 1. The purpose of this question was to find out if students know that a catalyst (whether homogeneous, heterogeneous or enzyme) works by providing a pathway of lower activation energy for the reaction to occur and that the mechanisms of the un-catalyzed and catalyzed reactions are different. If they are not able to correctly answer these questions with a high level of confidence, it would indicate that their conceptual understanding has not reached an acceptable level. If the selection frequency for the distracters for this question is at least 10% and with some level of confidence, then ACs related to these distracters are present (see the Discussion section for the ACs related to this question). Students are more familiar with the term ‘catalyst’, and we included ‘enzyme’ also in the responses related to the graphs to see whether they can recognize that it is also a (biological) catalyst.
A copy of the 13 page instrument is available as electronic supplementary material.
The content and context for each question are elaborated in the discussion section, where we discuss the ACs identified from each question.
The 4-tier version of the instrument, comprising 11 questions, was administered to another sample of students (N = 137). The time given for the test was an hour, and this was found to be more than adequate. Out of the 140 answer/reason combinations, there were zero selections for only two options in the instrument. This means that out of the 129 distracter combinations (since 11 answer/reason combinations represent correct responses), over 98% of the distracters were working. In view of this, it was considered not necessary to refine the instrument further. The data for this set of results are thus reported in this study.
Samples
The students who participated in this study have earlier covered the topic of reaction kinetics through lectures and tutorials over a period of at least 6 weeks. The choice of samples was predicated mainly by the willingness of schools to take part in the study. The participants were from schools in Singapore that offer A-level curricula. Ethics clearance for the study was obtained from the university's Institutional Review Board. Informed consent was obtained from the students (through their parents).The preliminary version of the instrument was administered to 96 students while 137 students took part in the next phase of the study. They were informed about the diagnostic test at least one week in advance so that they could revise the topic.
All students were in the age group 17–18 years. No data on ethnicity were collected as this is a potentially sensitive issue in the country. The ethnic make-up broadly mirrors the population profile in the country, that is, the students are mostly Chinese, followed by a much lesser number of Malays, then Indians and, lastly, other races.
Data analyses
The responses of the students were keyed into an Excel file for data analyses. It is a common practice to classify distracters with at least 10% selection as an AC, and this was followed in the identification of ACs.The ACs were further classified according to their CAC values (see definition below), as proposed by Caleon and Subramaniam (2010b):
Spurious ACs: CAC < 3.5
Moderate ACs 4.0 > CAC ≥ 3.5
Strong ACs: CAC ≥ 4.0
Further analyses were done by following the approach used by Caleon and Subramaniam (2010b) for their 4-tier instrument, and are given below:
Mean confidence (CF): adding confidence ratings for a question and dividing the total by number of students.
Confidence when correct (CFC): adding confidence ratings for a correctly answered question and dividing the total by the number of students who answered correctly
Confidence when wrong (CFW): adding confidence ratings for an incorrectly answered question and dividing the total by the number of students who answered incorrectly
Confidence with which an AC is expressed by students (CAC): adding the average confidence ratings for the answer and reason responses from which the AC was formulated, and dividing the total by the number of students who chose that answer–reason combination
Confidence discrimination quotient (CDQ): (CFC – CFW) divided by standard deviation across all confidence ratings
Confidence bias (CB): (CF – 1)/5 – (proportion of students who selected correct responses in both tiers).
Results
Instrument psychometrics
Table 2 shows how the students performed in the test as well as displays psychometric measures related to the questions. Though the diagnostic test aimed to ascertain students’ ACs on the relevant reaction kinetics concepts tested, it also doubled up as a test of their understanding of these concepts. Overall, and consistent with other studies in the literature, the test was on the difficult side. If correct responses for both tiers are required for full marks, then the mean score of the students was about 23%. If the test was marked on the basis of an MCQ test (that is, disregarding the reason tier), then, not surprisingly, the score is higher (47%). In keeping with other studies on two-tier tests, students had more difficulties with the reason tier than with the answer tier.| Question# | Proportion correct | A tier | R tier | B tier | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A tier | R tier | B tier | CF | CFC | CFW | CDQ | CB | CF | CFC | CFW | CDQ | CB | CF | CFC | CFW | CDQ | CB | |
| Note: A = answer, R = reason, B = both tiers combined. | ||||||||||||||||||
| 1 | 0.52 | 0.29 | 0.22 | 4.20 | 4.24 | 4.17 | 0.06 | 0.42 | 3.71 | 3.98 | 3.60 | 0.32 | 0.32 | 3.96 | 4.20 | 3.89 | 0.26 | 0.37 |
| 2 | 0.42 | 0.18 | 0.07 | 3.24 | 3.25 | 3.23 | 0.02 | 0.38 | 3.82 | 4.00 | 3.78 | 0.20 | 0.50 | 3.53 | 3.61 | 3.51 | 0.08 | 0.44 |
| 3 | 0.58 | 0.45 | 0.38 | 3.64 | 3.86 | 3.34 | 0.41 | 0.19 | 3.56 | 3.97 | 3.23 | 0.59 | 0.13 | 3.60 | 4.01 | 3.35 | 0.01 | 0.14 |
| 4 | 0.64 | 0.25 | 0.18 | 3.21 | 3.31 | 3.03 | 0.22 | 0.29 | 2.92 | 3.26 | 2.81 | 0.31 | 0.21 | 3.07 | 3.46 | 2.99 | 0.35 | 0.24 |
| 5 | 0.57 | 0.33 | 0.33 | 4.34 | 4.59 | 4.01 | 0.50 | 0.39 | 3.73 | 3.33 | 3.93 | −0.42 | 0.22 | 4.04 | 4.43 | 3.85 | 0.44 | 0.28 |
| 6 | 0.46 | 0.31 | 0.25 | 4.42 | 4.70 | 4.18 | 0.44 | 0.49 | 4.10 | 4.21 | 4.05 | 0.14 | 0.37 | 4.26 | 4.79 | 4.09 | 0.61 | 0.40 |
| 7 | 0.51 | 0.46 | 0.28 | 3.89 | 3.96 | 3.82 | 0.11 | 0.31 | 3.63 | 3.81 | 4.02 | 0.75 | 0.25 | 3.76 | 3.97 | 3.70 | 0.21 | 0.27 |
| 8 | 0.21 | 0.34 | 0.04 | 3.47 | 2.97 | 3.60 | −0.46 | 0.35 | 3.64 | 3.70 | 3.61 | 0.08 | 0.48 | 3.56 | 2.17 | 3.62 | −1.12 | 0.47 |
| 9 | 0.50 | 0.61 | 0.35 | 4.29 | 4.75 | 3.82 | 0.77 | 0.40 | 4.13 | 4.29 | 3.88 | 0.34 | 0.28 | 4.21 | 4.69 | 3.95 | 0.61 | 0.29 |
| 10 | 0.23 | 0.19 | 0.09 | 3.33 | 2.94 | 3.44 | −0.34 | 0.29 | 3.34 | 3.15 | 3.38 | −0.17 | 0.37 | 3.34 | 3.23 | 3.35 | −0.09 | 0.37 |
| 11 | 0.51 | 0.62 | 0.35 | 3.34 | 3.86 | 2.80 | 0.69 | 0.22 | 3.34 | 3.74 | 2.69 | 0.69 | 0.12 | 3.34 | 4.21 | 2.87 | 0.88 | 0.12 |
| Mean | 0.47 | 0.37 | 0.23 | 3.76 | 3.85 | 3.42 | 0.22 | 0.34 | 3.62 | 3.77 | 3.54 | 0.26 | 0.30 | 3.70 | 3.89 | 3.56 | 0.20 | 0.31 |
Cronbach alpha values for both the answer and reason tiers are low (Table 3) – when both tiers are considered together, the alpha value is higher. Consistent with other studies in the literature, alpha values for the respective confidence tiers are higher. Low values for Cronbach alpha for the cognitive scores were also obtained by Caleon and Subramaniam (2010a, 2010b) and Sreenivasulu and Subramaniam (2011, 2013) for their studies using multi-tier diagnostic instruments in the sciences.
| Tier | Cronbach alpha |
|---|---|
| Answer | 0.22 |
| Reason | 0.23 |
| Both (answer & reason) | 0.44 |
| Confidence (answer) | 0.85 |
| Confidence (reason) | 0.85 |
The low alpha value for cognitive tests is not necessarily a disadvantage in diagnostic tests as the principal objective was to identify ACs on reaction kinetics among students. In fact, Adams and Wieman (2011) suggest that it is alright for such tests to have a low alpha value. Moreover, the alpha value obtained from test scores with a sample of students is unique only to that sample and cannot be assumed to hold for another sample of students (Tavakol and Dennick, 2011). In fact, there is literature support to show that Cronbach alpha is not relevant for criterion-referenced tests such as diagnostic tests (Popham and Husek, 1969; Brown, 2002). Thus, for diagnostic instruments, the Cronbach alpha value is of less importance.
In a recent paper, Taber (2017) presented an excellent review on the use of Cronbach alpha in science education research and, at the same time, highlighted some issues to ponder on. The use of alpha as an index of uni-dimensionality is not unequivocally appropriate as the value can be inflated by the use of more items in the tests – likewise for alpha as a measure of reliability. Taber has noted that authors have seldom interpreted the alpha value beyond its supposed measures of reliability, internal consistency or dimensionality. We contribute to this discussion here.
In the computation of Cronbach alpha for diagnostic tests in the literature, it has to be noted that the scores of students for each question are used: 1 for correct response and 0 for incorrect response. That is, the Cronbach alpha value obtained is with respect to the cognitive scores. These scores have little relevance when an AC is framed on the basis of the incorrect responses for the answer–reason combination in such tests. Of course, in a test where all students have scored correctly for every question, then the use of Cronbach alpha is not appropriate as there is then zero variance among the items; no ACs can thus be documented.
The increase in Cronbach alpha value for the cognitive scores when both tiers are considered together can be explained on the basis of the greater internal consistency between the correct answer–reason combinations for the questions than when the responses for the individual tiers for the questions are considered separately. (Note that in this case, a score of 1 is given for a question only if both answer and reason are correct; for any other combinations, it is zero.) What this means is that the shared variance among the item responses is greater when the answer and reason tiers are considered together than when these are considered separately.
The increase in Cronbach alpha value for the confidence measures as compared to the cognitive measures is well noted in the literature for diagnostic tests (for example, Sreenivasulu and Subramaniam, 2014). It can be attributed to the greater internal consistency between the confidence measures as compared to the cognitive scores. However, the increase in Cronbach alpha value can also be due to the greater width of the confidence scale used – we used a 6-point scale ranging from Just guessing (1) to Absolutely confident (6), leading to greater variability in the responses than when a confidence scale with smaller width is used. It is noted in the literature that alpha is sensitive to the Likert scale width (Voss et al., 2000), with larger width scales contributing to higher values of alpha – confidence scales are similar to Likert scales.
ACs on reaction kinetics and associated confidence measures
Table 4 shows the various ACs identified in this study, and these have been classified into broad categories. Of interest to note is that every question in the instrument managed to surface at least an AC – moreover, other than Q3, 5 and 9, the remaining questions surfaced at least two ACs. Based on the nomenclature proposed by Caleon and Subramaniam (2010b), 10 of the ACs can be classified as spurious ACs, 8 as moderate ACs and 7 as strong ACs.| S/N | Question (ans/reas) | Alternative conception | % sample with AC | CAC |
|---|---|---|---|---|
| Properties of catalysts | ||||
| 1 | 2ab | If the energy profile diagram of a catalyzed reaction shows three low maxima while that for the corresponding uncatalyzed reaction shows a single, high maximum, the catalyst could be either an enzyme, a homogeneous catalyst or a heterogeneous catalyst since these substances lower the energy barrier of the reaction by providing a pathway of lower enthalpy change. | 24 | 3.44 |
| 2 | 2bb | If the energy profile diagram of a catalyzed reaction shows three low maxima while that for the corresponding uncatalyzed reaction shows a single, high maximum, the catalyst could be either a homogeneous or heterogeneous catalyst since these substances lower the energy barrier of the reaction by providing a pathway of lower enthalpy change. | 12 | 3.85 |
| 3 | 2cb | If the energy profile diagram of a catalyzed reaction shows three low maxima while that for the corresponding uncatalyzed reaction shows a single, high maximum, the catalyst could be either a heterogeneous catalyst or an enzyme since these substances lower the energy barrier of the reaction by providing a pathway of lower enthalpy change. | 12 | 3.56 |
| 4 | 4aa | For the catalyzed reaction A + B → C + D, when the rate of reaction is plotted against the concentration of one reactant (while keeping the other constant), the high initial dependence of rate on concentration followed by a levelling off of the graph at high concentration shows that the catalyst is not an enzyme since there is an optimum reactant concentration at which the enzyme would work at maximum efficiency. | 11 | 2.97 |
| 5 | 4ba | For the catalyzed reaction A + B → C + D, when the rate of reaction is plotted against the concentration of one reactant (while keeping the other constant), the high initial dependence of rate on concentration followed by a levelling off of the graph at high concentration shows that the catalyst could be an enzyme since there is an optimum reactant concentration at which the enzyme would work at maximum efficiency. | 27 | 3.21 |
| 6 | 4bc | For the catalyzed reaction A + B → C + D, when the rate of reaction is plotted against the concentration of one reactant (while keeping the other constant), the high initial dependence of rate on concentration followed by a levelling off of the graph at high concentration shows that the reaction could be homogenously catalyzed since the rate of reaction is proportional to reactant concentration. | 11 | 3.13 |
| Relationship between chemical equilibrium and rate of reaction | ||||
| 7 | 5bb | At higher temperatures, the yield of ammonia in the Haber process decreases but its rate of production increases, since the frequency of collisions of reactant molecules increases and the reverse reaction is favored. | 15 | 4.41 |
| 8 | 6ad | If a reversible exothermic reaction between two reactants is repeated at a higher temperature, equilibrium is reached faster but the equilibrium position remains unchanged since the initial reactant concentrations have not changed. | 24 | 4.33 |
| 9 | 6ba | If a reversible exothermic reaction between two reactants is repeated at a higher temperature, equilibrium is reached faster and more reactants remain at equilibrium, since the reverse reaction is favored and the forward reaction is impeded. | 19 | 4.08 |
| 10 | 7aa | In an all-gas, reversible, catalyzed reaction involving two reactants and two products, the net rate of formation of one product may be decreased only by reducing the initial concentration of one reactant or by continuously removing the other product since the rate of reaction will decrease and the position of the equilibrium will change under these conditions. | 13 | 3.64 |
| 11 | 7ab | In an all-gas, reversible, catalyzed reaction involving two reactants and two products, the net rate of formation of one product may be decreased only by reducing the initial concentration of one reactant or by continuously removing the other product since the rate of reaction remains the same but the position of the equilibrium changes under these conditions. | 15 | 4.14 |
| Relationship between activation energy, Boltzmann distribution and the effect of temperature increase on the rate of reaction | ||||
| 12 | 8aa | For two reactions with different activation energies but with the same rate constant at room temperature, an increase in temperature will cause the reaction with the smaller activation energy to have a higher rate constant because the molecules will collide more frequently and there will be a larger percentage increase in the proportion of molecules with energy greater than or equal to the activation energy for this reaction. | 46 | 3.42 |
| 13 | 8ac | For two reactions with different activation energies but with the same rate constant at room temperature, an increase in temperature will cause the reaction with the smaller activation energy to have a higher rate constant because there will be a larger percentage increase in the proportion of molecules with energy greater than or equal to the activation energy for this reaction. | 28 | 3.97 |
| 14 | 8ba | For two reactions with different activation energies but with the same rate constant at room temperature, an increase in temperature will cause the reaction with the higher activation energy to have a higher rate constant because the molecules will collide more frequently and there will be a larger percentage increase in the proportion of molecules with energy greater than or equal to the activation energy for this reaction. | 12 | 3.53 |
| 15 | 10aa | Given two reversible reactions, 1 (exothermic, high activation energy) and 2 (endothermic, low activation energy), an increase in temperature will result in the greatest percentage increase in the rate of reaction 1 forward because this reaction is the most exothermic. | 11 | 2.33 |
| 16 | 10cb | Given two reversible reactions, 1 (exothermic, high activation energy) and 2 (endothermic, low activation energy), an increase in temperature will result in the greatest percentage increase in the rate of reaction 2 forward because this reaction is the most endothermic. | 12 | 3.91 |
| 17 | 10cd | Given two reversible reactions, 1 (exothermic, high activation energy) and 2 (endothermic, low activation energy), an increase in temperature will result in the greatest percentage increase in the rate of reaction 2 forward because this reaction has the lowest activation energy, hence the largest percentage increase in fraction of molecules with energy greater than or equal to the activation energy. | 16 | 4.05 |
| 18 | 10dd | Given two reversible reactions, 1 (exothermic, high activation energy) and 2 (endothermic, low activation energy), an increase in temperature will result in the greatest percentage increase in the rate of reaction 2 backward because this reaction has the lowest activation energy, hence the largest percentage increase in fraction of molecules with energy greater than or equal to the activation energy. | 17 | 4.00 |
| Graphical representation of the Boltzmann distribution | ||||
| 19 | 9ab | As the temperature of a gas increases, the Boltzmann distribution curve for molecular speeds broadens and shifts to the right, while the height of the maximum point remains constant since the molecules then have higher average energy while its total number remains constant. | 20 | 3.72 |
| Graphical representation of first-order reactions | ||||
| 20 | 1aa | A first order reaction A → B + C can be represented by only an exponential graph of reactant concentration against time since the half-life is constant. | 19 | 3.96 |
| 21 | 1ba | A first order reaction A → B + C can be represented by both an exponential graph of reactant concentration against time and a linear graph of reaction rate against reactant concentration with positive gradient and zero intercept, since the half-life is constant. | 22 | 4.28 |
| Reaction mechanisms | ||||
| 22 | 11aa | As long as a proposed mechanism is consistent with the overall reaction, it is valid. | 13 | 2.97 |
| 23 | 11ab | It is possible for two given mechanisms to be valid since their rate-determining steps are consistent with the given rate law. (Actually, only the rate-determining step of the second mechanism is consistent with the given rate law.) | 18 | 3.02 |
| 24 | 11ca | Only one mechanism (2) for the reaction is valid since it is consistent with the overall reaction. (Actually, both of the given mechanisms are consistent with the overall reaction.) | 11 | 2.57 |
| Relationship between the rate of disappearance of reactants, the rate of formation of products, and stoichiometry | ||||
| 25 | 3ba | In the reaction 3O2(g) → 2O3(g), the rate of disappearance of oxygen is equal to the rate of production of ozone. | 24 | 3.33 |
The confidence measures extracted for the test also allow for further insights to be gained into students’ performance. We focus more on both tiers as this would indicate to what extent students have a good overall understanding of the concept/s tested. Mean confidence when correct (CFC) was 3.89 (out of 6). Mean confidence when wrong (CFW) was 3.56 (out of 6). The CDQ values range between −1.12 and 0.88, with the mean hovering at 0.20. Only two of the questions have negative CDQ values. With respect to CB values, none of the questions elicited a negative value or zero.
Discussion
As a key topic in chemistry, it is not surprising that reaction kinetics has been the subject of continued interest among chemistry education researchers. A recent review (Bain and Towns, 2016) provides a very good overview of the research undertaken to study students’ understanding of this topic. The utility of that review is further underscored by the listing of various ACs on this topic. The review also reinforces the point that the grade 12 level has attracted limited attention. With a view towards addressing the limited number of studies at this level, the present study was undertaken.The results of this study suggest that reaction kinetics is a difficult topic even for grade 12 students, who represent about 30% of the grade 1 cohort who go on to this level. This is not surprising as studies on various topics in the sciences demonstrate that students have quite a number of ACs on various topics even after instruction (for example, Lee, 2007). The passing level for diagnostic tests is typically low as the distracters are commonly ACs derived from the literature or from preliminary studies with students – unlike those from high stakes examinations such as leaving level examinations. Students need to have a good conceptual grasp of the topic if they are to do well in such diagnostic tests.
The good number of ACs identified (25) suggests that the instrument developed is not only effective for this purpose but also useful for getting some sense of students’ understanding of the domain in reaction kinetics tested. Of interest to note is that every question in the instrument has managed to surface an AC. More importantly, 17 out of the 25 ACs found were from the seven questions that featured graphs. Generally, in most diagnostic instruments there is a tendency to use, as far as possible, text-based questions. There could be two reasons for this – firstly, graphs take up more space and their inclusion can lengthen the instrument further; and secondly, since diagnostic instruments are generally short instruments, text-based instruments afford a more parsimonious way of testing the understanding of some of the key concepts and thus identifying ACs. However, graph-based questions do play a role as well in diagnostic testing. For example, besides the text in the answer and reason tiers, the presence of graphs affords an opportunity to surface ACs from a representation (graph) commonly used in chemistry and the extra cognitive processing that is likely to be involved in such questions can help to unpack students’ thinking further in the process of answering the questions. Indeed, visualization is a key aspect of scientific thinking as besides the medium of the text, representations such as graphs and images do exert importance in communication (Ainsworth et al., 2011) and, by implication, on students’ understanding. The graph representation thus offers a useful opportunity in identifying ACs as well.
ACs on reaction kinetics
We present a commentary on the various ACs found in our study. As far as possible, this is from the lens of our teaching experience. For convenience, we have grouped the ACs under conceptual categories:Question 4 refers to the reaction A + B → C + D, which is catalyzed by X, and shows the graph of the reaction rate versus concentration of A (while keeping [B] constant) having a steep curve at the start before leveling off after a while. It asserts that X could be an enzyme, a homogeneous catalyst or a heterogeneous catalyst, and students need to say whether it is true or false, with a reason. The fact that a catalyst speeds up a reaction is well known to students – that they function at near maximum efficiency at high reactant concentrations is often not readily apparent to them or is not adequately emphasized during teaching. An inadequate understanding of the latter concept could be the basis for the three ACs emerging from the response combinations to this question. Further to our commentary on the ACs on catalysts emerging from Q2, we note here that while the ACs reported in the literature on catalysts were derived from non-graph contexts, it seems that the graphical context used in our questions calls for extra cognitive processing by students on top of the text representation – and, by implication, making the navigation between multiple representations somewhat onerous. Some support for this argument is afforded by the work of Ainsworth (2006) who noted that navigation in a graphical representation poses problems if students do not have a proper understanding of the semantics of that representation – this could also be a possible reason for the students harboring these ACs.
Question 6 provides a graph showing how the concentration of a reactant varies as a function of time as it reacts exothermically with another reactant to reach equilibrium, and then queries which one of the three graphs in the answer tier would be obtained if the reaction were to be repeated at a higher temperature but with the same initial concentrations of the reactants, and the reason. Students need to keep in mind that when the temperature is increased, the rates of both the forward and reverse reactions are increased but the reverse reaction is favored – that means the correct graph would be the one which has a steeper initial slope (equilibrium is attained faster) but levels off at a higher reactant concentration (equilibrium favors reactants). Both the ACs obtained from this question can be traced to the students’ inadequate understanding of these concepts. The cognitive load required to apply all the above concepts and interpret the graph at the same time may also have overwhelmed some of the students. Again, we note that while the ACs reported in the literature in relation to the change of temperature on a system at equilibrium have been derived from non-graph contexts – for example, Hackling and Garnett (1985), it seems that these ACs persist even when a graphical context is used in tandem with text in our question. As mentioned earlier, the extra cognitive processing needed by students could have made navigation between multiple representations somewhat challenging.
Question 7 refers to a catalyzed reversible reaction P(g) + Q(g) → R(g) + S(g) and shows on the same axes of partial pressure of R against time, the profiles of two experiments. It asks which of the given three conditions could have caused the change from the profile with a steeper initial slope and a higher final partial pressure, to the profile with a smaller initial gradient and a smaller final partial pressure, and the reason. Clearly for the given conditions, the change in profile (reflecting a slower rate of formation and lower yield of R) could be caused either by less of P being used or a less efficient catalyst being used. The other option given – one of the products (S) being continually removed from the vessel, is not valid since this would increase the partial pressure of R as, according to Le Chatelier's principle, more of the reactants would then react to replenish the concentration of S in the system. The two ACs uncovered are thus due to students’ poor grasp of Le Chatelier's principle. Interestingly, none of the students showing these ACs considered the option “a different catalyst was used”. They may have been fixated on the idea that catalysts speed up reactions, hence the possibility of a catalyzed reaction slowing down due to the use of a less efficient catalyst escaped them. ACs related to Le Chatelier's principle (Cheung, 2009), partial pressure (Cheung et al., 2009) and catalysts (Kurt and Ayas, 2012) have been documented in simple contexts but the uncovering of more nuanced forms of ACs from contexts involving graphs related to a reversible reaction is a point of interest in our study, and further reinforces the tenaciousness with which ACs are entrenched among students.
Question 10 asks which one of the two reversible reactions: 1 (exothermic, high activation energy) or 2 (endothermic, low activation energy), represented graphically as reaction profiles, will show the greatest percentage increase in the rate of reaction for a given increase in temperature, and the reason. Students need to bear in mind that the higher the activation energy, the larger the percentage increase in the fraction of molecules with energy greater than or equal to the activation energy when the temperature is increased – that is, reaction 1 backward. Students had considerable difficulties in answering this question as it produced four ACs! Two of the ACs (10cd and 10dd) reflect the AC that the percentage increase in the fraction of molecules with energy greater than or equal to the activation energy is larger for the reaction with lower activation energy (the same as in Question 8, thus confirming the ubiquity of this AC). The other two ACs (10aa and 10cb) arise from the erroneous notion that the increase in the rate has to do with whether the reaction is exothermic or endothermic. ACs on activation energy with respect to the increase of temperature for reactions in equilibrium are not new and have been reported in the literature (for example, Hackling and Garnett, 1985) but the graphical contexts in which these have been derived from in our study have allowed us to frame these in a form that has not been reported in the literature.
Mechanism 1:
| 2ICl(g) → Cl2(g) + I2(g) slow |
| Cl2(g) + H2(g) → 2HCl(g) fast |
Mechanism 2:
| H2(g) + ICl(g) → HCl(g) + HI(g) slow |
| HI(g) + ICl(g) → HCl(g) + I2(g) fast |
The rate law of a reaction is very much dependent on the rate-determining step. Since the order of the reaction is one for each reactant, it follows that both feature in the rate-determining step, hence the second mechanism would be consistent with the overall kinetics of the reaction. That three ACs were found from this question suggests that a good number of students have difficulties with the topic of reaction mechanisms. A significant proportion of students (24%, combining 11aa and 11ca) thought that a proposed mechanism is valid as long as it is consistent with the overall reaction. Approximately half of this group of students also have difficulty judging whether a particular mechanism is consistent with the overall reaction (11ca). Another group of students (18%, 11ab) are aware that for a mechanism to be valid, it must also feature a rate-determining step that is consistent with the rate law – however, they have difficulties identifying the mechanism where the rate-determining step is consistent with the rate law. As the concepts involved are not complex, we believe that the above ACs stem more from a lack of guided practice in analyzing reaction mechanisms than from poor conceptual understanding. ACs on the kinetics of reaction mechanisms seem to have been given limited, if any, attention in the literature.
General comments
When comparing the ACs framed in our study with those listed in the recent comprehensive review by Bain and Towns (2016) as well as in the recent study by Yan and Subramaniam (2016), it can be seen that except for the one AC derived from Q8, all the other framed ACs from our study have not been reported before.Confidence measures
The mean score for the test was about 23% (with both tiers correct) and this was accompanied by a mean confidence value of about 3.89 (out of 6). This does not represent a particularly good understanding of the topic tested. In other words, the deficit in confidence, 2.11 (out of 6), represents the gap in understanding that needs to be bridged if students were to be fully confident of the correctness of their responses in relation to these questions. If this were to be extended to the remaining questions in the test, it is clear that the deficit in understanding that needs to be bridged for obtaining maximal certainty in the correctness of their responses is even more overwhelming. The findings further underscore the limitations of traditional MCQs in testing students’ understanding – as expected, an inflated mean score (47%) is obtained if we consider only the answer tier, and this is accompanied by a mean confidence of 3.85. Clearly, there are advantages in using answer/reason combinations for testing students’ understanding compared to just relying on the answer. It is the inclusion of confidence scales to both tiers of the instrument that have made it possible for further insights to be gained on top of the cognitive scores (see for example, Hoe and Subramaniam, 2016).The CFC value of 3.89 (out of 6) suggests that even when students are correct, they were not able to assign the highest possible confidence rating for the certainty of their responses. Also, the CFW value of 3.56 suggests that even when students are wrong, they did not assign the lowest possible confidence rating – this means that their responses are unlikely to be due to a lack of knowledge or pure guessing but more due to ACs. For the two questions that have negative CDQ values, it means that students were more confident when they were wrong than when they were correct. The low value of the mean CDQ further suggests that the discriminating powers of the students between what they know and what they do not know, overall, are on the low side (Lundeberg et al., 2000). With respect to CB values, none of the questions elicited a negative value or zero – this means that, overall, students were overconfident in the certainty of their responses.
Looking at the nature of the ACs on the basis of the confidence with which these are expressed, we argue that some of the ACs in the spurious and moderate categories can well be classified as strong ACs. It is likely that the classification scheme proposed by Caleon and Subramaniam (2010b) is quite stringent for use in our case. For example, the AC derived from Q8aa, which has a CAC value of 3.42 and is harbored by nearly half of the sample, points to fundamental issues with understanding how two reactions with the same rate constant at room temperature but with different activation energies will behave at a higher temperature. Students need to activate multiple concepts – for example, activation energy, rate constant, Boltzmann distribution and the rate of reaction, before they can cognize the nuances of the responses featured in the response tiers to arrive at the correct answer/reason combination. Thus, it is unlikely to be a spurious AC but more a strong AC. Likewise, in relation to the AC derived from Q2bb, which has a CAC value of 3.85 and is held by about 12% of the sample, students need negotiation of understanding across multiple concepts – for example, homogeneous catalysts, heterogeneous catalysts, energy profile diagrams, activation energy and enthalpy change, before they can sieve the correct response combinations from the ‘noise’ offered not only by the incorrect distracter combinations but also by the correct answer/incorrect reason as well as incorrect answer/correct reason combinations. Thus, this moderate AC is also more likely to be a strong AC.
Utility of the 4-tier format
The findings of this study reiterate that the 4-tier format proposed in the literature is effective for identifying ACs as well as in ascertaining student understanding of a topic. The good number of ACs derived from the administration of the instrument as well as the confidence measures associated with these have allowed for a more nuanced classification of the ACs and one that is more robust in segregating genuine misconceptions from just incorrect responses.Implications
Even on selected aspects of the topic of reaction kinetics, the students in this study held a range of ACs, with varying confidence levels. This was after they have been taught the topic through lectures as well as problem-solving through tutorials plus some time to revise the topic. Obviously, the traditional approach of teaching has not been especially effective in promoting good conceptual understanding as well as in pre-empting the emergence of ACs in students. The instrument developed for this study can be used by teachers to uncover ACs on aspects of reaction kinetics among their students and act on remediating any identified ACs. With knowledge of the common ACs on reaction kinetics and the availability of diagnostic instruments, teachers would be in a better position to recalibrate their pedagogy in lesson delivery for the next cycle of lessons.The good number of studies on ACs in the science education literature have contributed significantly to our understanding of various topics. There is also a need to document confidence-related measures in relation to these ACs as these can provide some sense of how firmly entrenched these ACs are among students. Also, psychometric measures such as CFC, CFW, CDQ and CB can help to contribute to better appreciation of how students have performed in the test. Almost all studies in the literature related to ACs on reaction kinetics have documented ACs without differentiating whether these are due to a lack of knowledge or genuine misconceptions. One exception is the study reported by Yan and Subramaniam (2016) who used a 3-tier format, which has a common confidence rating for both the answer and reason tiers. The results of this study reiterate the point that students have different degrees of confidence for the answer and reason tiers, and hence it is more prudent to have separate confidence scales for these tiers. Identification of genuine ACs is important as pedagogical resources can then be deployed more for addressing these ACs. Clearly, the 4-tier format is a viable tool for probing students’ understanding as well as in identifying ACs in science.
Limitations
The results of this study cannot be generalized to the entire grade 12 cohort in the schools or the country as only a small fraction of them participated in the test. Also, the performance of the students in the test cannot be taken as a proxy for their overall proficiency in reaction kinetics as such instruments, by their very nature, can test only on selected aspects of the topic. It is assumed, like in other studies involving student rating of confidence for a response, that our sample of students gave a confidence rating that reflected their own feeling for their certainty of their response. Our findings must thus be viewed in these contexts.Conclusion
The 11-item, 4-tier diagnostic instrument on reaction kinetics developed for this study has surfaced 25 ACs among grade 12 students. Except for one AC, the other framed ACs have not been reported in the literature. The ACs uncovered in this study relate more to difficult contexts in reaction kinetics than those generally reported in the literature. A number of these ACs arose because students need to navigate among multiple concepts in reaction kinetics within a single question. We used questions involving multiple concepts in developing the instrument since such questions are more effective in testing students’ conceptual understanding and uncovering ACs in more difficult contexts. The list of ACs would be useful to teachers at the grade 11–12 level. Psychometric measures related to confidence with respect to accuracy of the responses have been provided. Very few studies on ACs in the science education literature present such data, which are useful in differentiating ACs due to genuine misconceptions from those arising due to lack of knowledge as well as providing other metacognitive information. Such information is not possible to obtain from traditional MCQs or two-tier diagnostic instruments. Clearly, the diagnostic usefulness of the instrument can be considered to be good. To this extent, the 4-tier format offers significant advantages over ordinary MCQs and two-tier MCQs, and is effective for probing students’ understanding of a topic as well as for identifying ACs more robustly. There is a need for more studies using the 4-tier format to diagnose ACs on different topics in the sciences as such studies are rather few in the science education literature.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the Office of Education Research (National Institute of Education, Nanyang Technological University) for the award of a research grant (OER 40/08/RS) for this study. We also thank one of the reviewers as well as the Editor, Prof. Keith Taber, for useful and constructive feedback on an earlier version of our manuscript (The views expressed in this paper represent those of the authors and do not necessarily represent those of any of the national agencies mentioned).References
- Adams W. K. and Wieman C. E., (2011), Development and validation of instruments to measure learning of expert-like thinking, Int. J. Sci. Educ., 33(9), 1289–1312.
- Ainsworth S., (2006), DeFT: A conceptual framework for considering learning with multiple representations, Learn. Instr., 16(3), 183–198.
- Ainsworth S., Prain V. and Tytler R., (2011), Drawing to learn in science, Science, 333 (6046), 1096–1097.
- Akkus H., Kadayifçi H., Atasoy B. and Geban Ö., (2003), Effectiveness of instruction based on the constructivist approach on understanding chemical equilibrium concepts, Res. Sci. Technol. Educ., 21, 210–227.
- Amir R. and Tamir P., (1994), In-depth analysis of misconceptions as a basis for developing research-based remedial instruction: the case of photosynthesis, Am. Biol. Teach., 56(2), 94–100.
- Arslan H. O., Cigdemoglu C. and Moseley C., (2012), A three-tier diagnostic test to assess pre-service teachers’ misconceptions about global warming, greenhouse effect, ozone layer depletion, and acid rain, Int. J. Sci. Educ., 34(11), 1667–1686.
- Ausubel D. P., Novak J. D. and Hanesian H., (1978), Educational Psychology: A Cognitive View, 2nd edn, New York: Holt, Rinehart and Winston.
- Bain K. and Towns M. H., (2016), A review of research on the teaching and learning of chemical kinetics, Chem. Educ. Res. Pract., 17(2), 246–262.
- Brown J. D., (2002), The Cronbach alpha reliability estimate, JALT Testing & Evaluation SIG Newsletter, 6(1), 17–18.
- Çakmakci G., (2010), Identifying alternative conceptions of chemical kinetics among secondary school and undergraduate students in Turkey, J. Chem. Educ., 87, 449–455.
- Caleon I. and Subramaniam R., (2010a), Development and application of a three-tier diagnostic test to assess secondary students’ understanding of waves, Int. J. Sci. Educ., 32, 939–961.
- Caleon I. and Subramaniam R., (2010b), Do students know what they know and what they do not know? Using a four-tier diagnostic test to assess the nature of students’ alternative conceptions, Res. Sci. Educ., 40, 313–337.
- den Broek V. P., (2010), Using texts in science education: Cognitive processes and knowledge representation, Science, 328(5977), 453–456.
- Cheung D., (2009), The adverse effects of Le Chatelier's principle on teacher understanding of chemical equilibrium, J. Chem. Educ., 86(4), 514.
- Cheung D., Ma H. J. and Yang J., (2009), Teachers’ misconceptions about the effects of addition of more reactants or products on chemical equilibrium, Int. J. Sci. Math. Educ., 7(6), 1111–1133.
- Duit R., (2009), Bibliography—Students’ and teachers’ conceptions and science education. Available at: http://www.ipn.uni-kiel.de/aktuell/stcse/stcse.html.
- Gilbert J. K. and Watts D. M., (1983), Concepts, misconceptions and alternative conceptions: Changing experiences in science education, Stud. Sci. Educ., 10, 61–98.
- Hackling M. W. and Garnett P. J., (1985), Misconceptions of chemical equilibrium, Eur. J. Sci. Educ., 7(2), 205–214.
- Hoe K. Y. and Subramaniam R., (2016), On the prevalence of alternative conceptions on acid–base chemistry among secondary students: insights from cognitive and confidence measures, Chem. Educ. Res. Pract., 17(2), 263–282.
- Justi R., (2003), Teaching and learning chemical kinetics, Chemical Education: Towards Research-based Practice, Springer Netherlands, pp. 293–315.
- Kalina C. and Powell K. C., (2009), Cognitive and social constructivism: Developing tools for an effective classroom, Education, 130(2), 241–250.
- Kaya E. and Geban Ö., (2012), Facilitating conceptual change in rate of reaction concepts using conceptual change oriented instruction, Educ. Sci., 37, 216–225.
- Klassen S., (2006), Contextual assessment in science education: Background, issues, and policy, Sci. Educ., 90(5), 820–851.
- Kırık Ö. T. and Boz Y., (2012), Cooperative learning instruction for conceptual change in the concepts of chemical kinetics, Chem. Educ. Res. Pract., 13 (3), 221–236.
- Kolomuç A. and Tekin S., (2011), Chemistry teachers’ misconceptions concerning concept of chemical reaction rate, Eur. J. Phys. Chem. Educ., 3(2), 84–101.
- Kurt S. and Ayas A., (2012), Improving students’ understanding and explaining real life problems on concepts of reaction rate by using a four step constructivist approach, Energy Educ. Sci. Technol., Part B: Soc, Educ. Stud., 4(2), 979–992.
- Lee S. J., (2007), Exploring students’ understanding concerning batteries—Theories and practices, Int. J. Sci. Educ., 29(4), 497–516.
- Lin S. W., (2004), Development and application of a two-tier diagnostic test for high school students’ understanding of flowering plant growth and development, Int. J. Sci. Math. Educ., 2(2), 175–199.
- Lundeberg M. A., Fox P. W., Brown A. C. and Elbedour S., (2000), Cultural influences on confidence: country and gender, J. Educ. Psychol., 92(1), 152–159.
- McClary L. M. and Bretz S. L., (2012), Development and assessment of a diagnostic tool to identify organic chemistry students’ alternative conceptions related to acid strength, Int. J. Sci. Educ., 34(15), 2317–2341.
- Morrison J. A. and Lederman N. G., (2000), Science teachers’ diagnosis of students’ perceptions. Presented at the annual meeting of the National Association for Research in Science Teaching, New Orleans, LA.
- Odom A. L., (1995), Secondary & college biology students' misconceptions about diffusion & osmosis, Am. Biol. Teach., 409–415.
- Odom A. L. and Barrow L. H., (1995), Development and application of a two-tier diagnostic test measuring college biology students' understanding of diffusion and osmosis after a course of instruction, J. Res. Sci. Teach., 32(1), 45–61.
- Peşman H. and Eryılmaz A., (2010), Development of a three-tier test to assess misconceptions about simple electric circuits, J. Educ. Res., 103(3), 208–222.
- Popham W. J. and Husek T. R., (1969), Implications of criterion-referenced measurement, J. Educ. Meas., 6(1), 1–9.
- Reynolds C. R., Livingston R. B. and Willson V., (2006), Measurement and Assessment in Education, Boston: Pearson.
- Seçken N. and Seyhan H. G., (2015), An analysis of high school students' academic achievement and anxiety over graphical chemistry problems about the rate of reaction: The case of Sivas province, Procedia - Social and Behavioral Sciences, 174, 347–354.
- Sia D. T., Treagust D. F. and Chandrasegaran A. L., (2012), High school students’ proficiency and confidence levels in displaying their understanding of basic electrolysis concepts, Int. J. Sci. Math. Educ., 10(6), 1325–1345.
- Sreenivasulu B. and Subramaniam R., (2013), University students’ understanding of chemical thermodynamics, Int. J. Sci. Educ., 35(4), 601–635.
- Sreenivasulu B. and Subramaniam R., (2014), Exploring undergraduates’ understanding of transition metals chemistry with the use of cognitive and confidence measures, Res. Sci. Educ., 44(6), 801–828.
- Supasorn S. and Promarak V., (2015), Implementation of 5E inquiry incorporated with analogy learning approach to enhance conceptual understanding of chemical reaction rate for grade 11 students, Chem. Educ. Res. Pract., 16(1), 121–132.
- Tavakol M. and Dennick R., (2011), Making sense of Cronbach alpha, Int. J. Med. Educ., 2, 53–55.
- Taber K. S., (2000), Multiple frameworks?: Evidence of manifold conceptions in individual cognitive structure, Int. J. Sci. Educ., 22(4), 399–417.
- Taber K. S., (2017), The use of Cronbach's Alpha when developing and reporting research instruments in science education, Res. Sci. Educ., DOI:10.1007/s11165-016-9602-2.
- Tekin B. B. and Nakiboglu C., (2006), Identifying students' misconceptions about nuclear chemistry. A study of Turkish high school students, J. Chem. Educ., 83(11), 1712.
- Treagust D., (1986), Evaluating students' misconceptions by means of diagnostic multiple choice items, Res. Sci. Educ., 16(1), 199–207.
- Treagust D. F., (1988), Development and use of diagnostic tests to explore students’ misconceptions in science, Int. J. Sci. Educ., 10, 159–170.
- Tuŕanyi T. and Tóth Z., (2013), Hungarian university students' misunderstandings in thermodynamics and chemical kinetics, Chem. Educ. Res. Pract., 14, 105–116.
- Voska K. W. and Heikkinen H. W., (2000), Identification and analysis of student conceptions used to solve chemical equilibrium problems, J. Res. Sci. Teach., 37(2), 160–176.
- Voss K. E., Stem Jr. D. E. and Fotopoulos S., (2000), A comment on the relationship between coefficient alpha and scale characteristics, Marketing Letters, 11(2), 177–191.
- Wandersee J. H., Mintzes J. J. and Novak J. D., (1993), Research on alternative conceptions in science, in Gabel D. (ed.), NSTA Handbook: Research in Science Teaching, New York: Macmillan, pp. 177–209.
- Yalçınkaya E., Taştan-Kırık Ö., Boz Y. and Yıldıran D., (2012), Is case-based learning an effective teaching strategy to challenge students’ alternative conceptions regarding chemical kinetics? Res. Sci. Tech. Educ., 30(2), 151–172.
- Yan Y. K. and Subramaniam R., (2016), Diagnostic appraisal of grade 12 students’understanding of reaction kinetics, Chem. Educ. Res. Pract., 17(4), 1114–1126.
| This journal is © The Royal Society of Chemistry 2018 |