Open Access Article
Open Access ArticleTheoretical research on novel orthorhombic tungsten dinitride from first principles calculations
Qian Li *ab,
Jianyun Wangb and
Hanyu Liuc
*ab,
Jianyun Wangb and
Hanyu Liuc
aCollege of Aeronautical Engineering, Binzhou University, Binzhou 256600, China. E-mail: qianqianli527@126.com; Tel: +86-17862079360
bState Key Laboratory of Superhard Materials, Jilin University, Changchun 130012, China
cGeophysical Laboratory, Carnegie Institution of Washington, Washington, D.C. 20015, USA
First published on 5th March 2018
Abstract
Tungsten nitrides have been intensely studied for technological applications owing to their unique mechanical, chemical, and thermal properties. Combining first-principles calculations with an unbiased structural searching method (CALYPSO), we uncovered a novel orthorhombic structure with a space group Cmc21 as the thermodynamically most stable phase for tungsten dinitride (WN2) between 46–113 GPa. The computed elastic constants and phonons reveal that the Cmc21-WN2 structure is dynamically stable at atmospheric pressure. Moreover, hardness calculations indicate that this structure is likely to become a hard material. Our current results may stimulate further experimental work on synthesizing these technologically important materials and improve the understanding of the pressure-induced phase transitions of other transition-metal light-element compounds.
1. Introduction
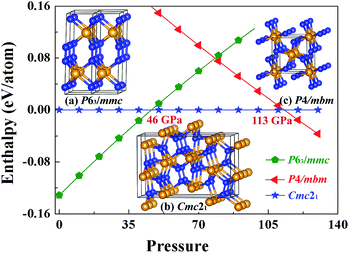
Tungsten nitrides have greater potential than other nitrides not only due to their mechanical, catalytic, optical, electronic, and hardness properties but also due to tungsten's wide availability, their economical synthesis and their varied possible stoichiometric compositions.1–4 These qualities make them practically useful in industrial applications such as in cutting tools, super-abrasive materials, and wear-resistant coatings, all leading them to be the subject of considerable research interest.5–15 In particular, tungsten nitrides (WN, W3N4, W2.25N3, W2N3) were recently successfully synthesized through new approaches involving metathesis reaction, solid-state ion exchange and nitrogen degassing under high pressure and high temperature (5 GPa, 880–2570 K;16 7.7 GPa, 1373–1973 K;17 600–675 °C (ref. 18)), which could be quenched and stabilized to ambient conditions. These have attracted significant attentions on these compounds and motivated considerable interest in searching for new tungsten nitrides. Theoretical researches also show that in nitrogen-rich materials the chemical bonding is strongly covalent so that they have high bulk modulus and high hardness such as Zr3N4,19 Hf3N4,19 PtN2,20,21 OsN2,22 and IrN2,22 synthesized under high pressure. Therefore, it is advantageous to choose nitrogen-enriched compounds using high-pressure methods in searching for new superhard materials. It is noteworthy that, in a very recent work, Lu et al. suggested WN is likely to become a superhard material (>40 GPa).15 Tungsten dinitride (WN2) is thus expected to be a good candidate for high hardness materials, since it possessed one more N atom per formula unit compared to WN.For a long time, WN2 has been theoretically suggested to adopt P63/mmc10 structure at atmosphere pressure. Other researchers proposed a tetragonal phase of WN2 through replacing the P4/mbm-ReN2 structure.11 In this work, we established thermodynamically stable structures of WN2 over a wide range of pressures combining the first-principles calculations with unbiased structural searching methods. A novel orthorhombic WN2 with a space group Cmc21 is predicted which is energetically superior to the previously proposed P63/mmc phase above 46 GPa and P4/mbm phase below 113 GPa. This structure is incompressible and has not been reported before. As this newly found structure is dynamically stable, it can be prepared at high-pressure and high-temperature and quenched recovered under atmospheric conditions. This work not only revised the phase diagram of WN2 at high pressures, but also provided useful information and important guidance for the further experimental synthesis and theoretical study of WN2.
2. Computational details
Our global structural prediction used the unbiased intelligence based on CALYPSO23–25 methods which have successfully predicted structures of various systems.26–30 The structural relaxations, electron localization function (ELF) and electronic band structure calculations were performed using the density functional theory within the local density approximation (LDA)31,32 as implemented in the Vienna ab initio simulation package (VASP) code.33 The electron–ion interaction was described by means of projector augmented wave (PAW)34 with 5d46s2 and 2s22p3 electrons as valence for tungsten and nitrogen atoms, respectively. The PAW34 method was adopted with a plane-wave kinetic-energy cutoff of 520 eV to give excellent convergence on the total energies and structural parameters. The Monkhorst–Pack (MP) k meshes35 0.025 Å−1 were chosen to ensure the energies of all structures were well converged to be better than 1 meV per atom. The phonon frequencies were calculated using the direct supercell method, which uses the forces obtained by the Hellmann–Feynman theorem calculated from the optimized supercell.36 Accurate crystal elastic constants and modulus were calculated by using the Voigt–Reuss–Hill approximation.37 The simulated micro hardness38,39 were used to evaluate the mechanical properties for these WN compounds.3. Results and discussion
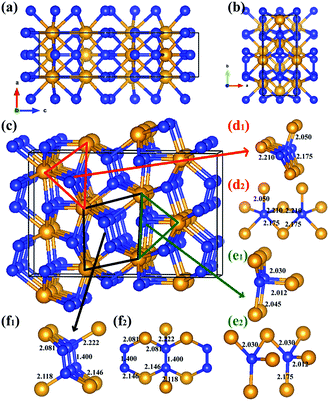
In the previous theoretical studies, Wang et al. predicted a hexagonal structure with space group P63/mmc10 which is potential ultra-incompressible and energetically superior to the previously proposed phase hence it is regarded as the ground state of WN2 up to 60 GPa. Yan et al.11 put forward a tetragonal phase of WN2 through replace the P4/mbm-ReN2 structure which exhibits an unusual incompressibility along the c axis on a par with diamond. This P4/mbm phase is dynamically stable, nevertheless, metastable compared to P63/mmc at 0 GPa.11 Due to the potential importance of this material, we have performed the systematical structural prediction for WN2 compound in the pressure range of 0–150 GPa (3–24 atoms for each pressure) using unbiased intelligence structural searches. Here, we found that three structures could exist in different pressure ranges [Fig. 1(a)–(c)]. Besides the ground state phase (P63/mmc)10 and high-pressure phase (P4/mbm)11 which fits well with previous researches, our structural search also successfully identified a new orthorhombic structure with a space group Cmc21 [Fig. 1(b)] as the thermodynamically most stable phase for WN2 between 46 and 113 GPa as shown in Fig. 1. It is noteworthy that this structure is more complex than the other two previous structures with higher symmetry. The present results revised the phase diagram of WN2 at high pressures.The equilibrium lattice parameter of the Cmc21-WN2 structure are a = 2.909 Å, b = 6.875 Å, c = 10.517 Å at 0 GPa while a = 2.802 Å, b = 6.721 Å, c = 10.153 Å at 50 GPa. There are eight WN2 formula units in the unit cell, and the tungsten atoms occupied the Wyckoff 4d(0, 0.150, 0.581), 4d(0.500, 0.942, 0.792), while the nitrogen atoms at the 8b(0.500, 0.774, 0.231), 8b(0.000, 0.247, 0.947) positions. The density of Cmc21-WN2 is 13.383 g cm−3 at 0 GPa. Through observation of Cmc21-WN2 along the A axis, we prove that the structure is arranged in a neat layer while disordered along other directions [Fig. 2(a) and (b)]. Besides, this phase consists of a fundamental building block connected by irregular rings [Fig. 2(c)]. We have selected three representative bonding modalities of nitrogen atoms in the Cmc21-WN2 structure and exhibited in different crystallographic planes. The first kind of nitrogen atom has five neighboring tungsten atoms [Fig. 2(d)] with W–N bond lengths of 2.050 Å, 2.175 Å and 2.210 Å. The other two kinds of nitrogen atoms have four neighboring atoms. By contrast, one of them is adjacent to four tungsten atoms [Fig. 2(e)] while another one has a neighboring nitrogen atom [Fig. 2(f)]. The bond lengths are shown in the Fig. 2. It is worth noting that the N–N bond length is 1.400 Å at 0 GPa while 1.364 Å at 50 GPa [Fig. 2(f)].
We calculated the charge density distribution and Electron Localization Function (ELF) that enables an effective and reliable analysis of the interaction between atoms. Here, we use a high isosurface value of 0.8 which indicates the possible formation of strong covalent bonds.40,41 Previous studies have shown that an important ultra-incompressible effect comes from strong covalent N–N bonding.20,21 High electron localization can be clearly seen in the region between adjacent N–N and W–N bonds, indicative of strong covalent bonding (Fig. 3). As shown in the Fig. 3, the bonding environment of nitrogen atoms is much more complex. The calculated ELF exhibits that some nitrogen atoms in Cmc21-WN2 structure are fourfold coordinated with three near-neighbor tungsten atoms and one nitrogen atom hence forming a three-dimensional covalently bonded framework. Some nitrogen atoms are five-coordinated with neighboring tungsten atoms. The other nitrogen atoms are four-coordinated and forming a stable sp3 bonding state with tungsten atoms. These strong three-dimensional covalent bonds could reasonably lead to super hardness properties of Cmc21-WN2 structure. The calculated charge of Cmc21-WN2 showed there is the charge transfer between W (∼2.774) and N (1.449 and 1.327) atoms.
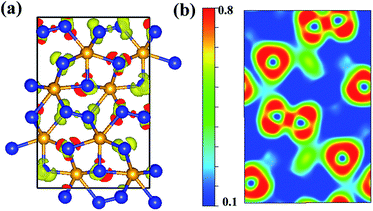 | ||
| Fig. 3 Contours of the ELF of Cmc21-WN2with isosurface = 0.8. The 2D-ELF is given for better observation. | ||
As the strong covalent W–N and N–N bonding play a key role in the ultra-incompressibility, Cmc21-WN2 may become one of the potential candidates for superhard materials. It is of the fundamental importance to compute the mechanical properties and hardness of WN2. The computed elastic constants (Cij) are listed in Table 1 as well as the previously predicted P63/mmc and P4/mbm for comparison. It is well known that, for orthogonal structure, the mechanical stability requires that the elastic constants have to satisfy the following conditions:42 Cii >0 (i = 1–6), C11 + C22 + C33 + 2(C12 + C13 + C23) > 0, C11 + C22 − 2C12 > 0, C11 + C33 − 2C13 > 0, C22 + C33 − 2C23 > 0. For tetragonal and hexagonal structures, the Cij's need satisfy the following conditions: C11 > 0, C33 > 0, C44 > 0, C66 > 0, (C11 − C12) > 0, (C11 + C33 − 2C13) > 0, 2(C11 + C12) + C33 + 4C13 > 0 and C44 > 0, C11 > |C12|, (C11 + C12) × C33 > 2C12,2 respectively. The elastic constants in Table 1 satisfy all of the conditions above, indicating they are mechanically stable.
The bulk moduli (B) of Cmc21-WN2 (437 GPa) is larger than the other two structures, which is comparable to the experimental value of diamond of 446 GPa (ref. 43) and indicate its ultra-incompressible nature. The ratio of B and shear modulus G for these structures are found lower than 1.75 (threshold for a material becoming ductile), indicating that these three WN2 compounds are brittle material. In addition, the calculated Young's modulus for novel Cmc21-WN2 is much lower than that of other two phases. The Vickers hardness of the Cmc21-WN2 was calculated both using a semiempirical model designed for covalency dominant crystals in particular transition-metal carbides and nitrides (eqn (1))38 and a theoretical model which establishes a robust correlation between hardness and elasticity (eqn (2)),39
| Hv (GPa) = 1051 Ne2/3d−2.5e−1.191fi−32.2fm0.55 | (1) |
| Hv = 2(k2G)0.585 − 3 | (2) |
Furthermore, we have investigated the electronic properties of the predicted structure. The band structure of Cmc21-WN2 is plotted in Fig. 4(a) together with the corresponding partial density of states (PDOS). It is found that the Cmc21-WN2 structure is shown to be metallic with the majority of the DOS near the Fermi level contributed by p-states of nitrogen and d-states of tungsten. Strong hybridization between the W-d and N-p orbitals suggests the strong covalent bonding between the W and N atoms, in satisfactory agreement with the ELF analysis. The pronounced peaks in the DOS of Cmc21-WN2 correspond to flat bands in the band structure. Phonon calculation played a key role in understanding the dynamic stabilities of the predicted structures. The calculations on phonon dispersion clearly show that there is no imaginary phonon frequency in the whole Brillouin zones of Cmc21-WN2 [Fig. 4(b)], indicating this structure is dynamically stable at ambient pressure that thus suggest the predicted structure could in principle be experimentally synthesized and quenched recovered to atmospheric conditions. We have also investigated the P63/mmc and P4/mbm as well, and the results reveal the both structures are dynamically stable.10,11
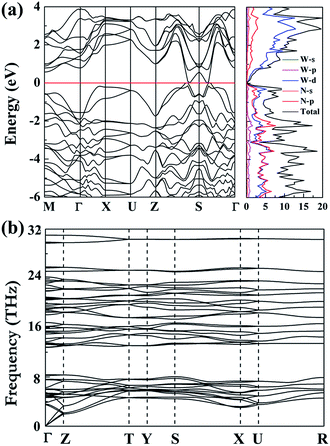 | ||
| Fig. 4 Calculated band, dos (a) and phonon dispersion curves (b) of the Cmc21-WN2 at the atmospheric conditions. | ||
4. Conclusion
In summary, we have performed the simulations on the thermodynamically stable structures of WN2 over a wide range of pressures combining the first-principles calculations with unbiased structural searching method. We uncovered a novel orthorhombic structure with a space group Cmc21 as the thermodynamically most stable phase for WN2 between 46–113 GPa. A comprehensive study of the elastic properties, ELF and hardness demonstrated that the novel Cmc21-WN2 exhibit excellent mechanical and ultra-incompressible properties. No imaginary phonon frequencies indicate that the structure is dynamically stable therefore it can be prepared at high-pressure and high-temperature and quenched recovered to atmospheric conditions. These findings will inevitably stimulate extensive experimental works on synthesizing these technologically important materials and theoretical work to explore the rich and complex phases of transition-metal and light-element compounds.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the Natural Science Foundation of China under No. 11747049, Shandong Provincial Natural Science Foundation of China under Grant No. ZR2017LA008, Science Foundation of Binzhou University under Grant No. 2016Y03.References
- S. Anwar, Surf. Eng., 2017, 33, 276 CrossRef CAS.
- P. Nayak, S. Anwar, S. Bajpai and S. Anwar, in AIP Conference Proceedings, 2017, vol. 1832, p. 080063 Search PubMed.
- N. Schönberg, Acta Chem. Scand., 1954, 8, 204 CrossRef.
- M. Zhang, Y. Qiu, Y. Han, Y. Guo and F. Cheng, J. Power Sources, 2016, 322, 163 CrossRef CAS.
- Y. Shen, Y. Mai, D. R. McKenzie, Q. Zhang, W. D. McFall and W. E. McBride, J. Appl. Phys., 2000, 88, 1380 CrossRef CAS.
- M. J. Mehl, D. Finkenstadt, C. Dane, G. L. Hart and S. Curtarolo, Phys. Rev. B, 2015, 91, 184110 CrossRef.
- P. Hones, N. Martin, M. Regula and F. Lévy, J. Phys. D: Appl. Phys., 2003, 36, 1023 CrossRef CAS.
- Y. Dong and J. Li, Chem. Commun., 2015, 51, 572 RSC.
- Q. Li, L. Sha, C. Zhu and Y. Yao, Europhys. Lett., 2017, 118, 46001 CrossRef.
- H. Wang, Q. Li, Y. Li, Y. Xu, T. Cui, A. R. Oganov and Y. Ma, Phys. Rev. B, 2009, 79, 132109 CrossRef.
- H. Yan, M. Zhang, Q. Wei and P. Guo, J. Alloys Compd., 2013, 581, 508 CrossRef CAS.
- Z. Zhao, K. Bao, D. Duan, F. Tian, Y. Huang, H. Yu, Y. Liu, B. Liu and T. Cui, Phys. Chem. Chem. Phys., 2015, 17, 13397 RSC.
- Z. Liu, X. Zhou, D. Gall and S. Khare, Comput. Mater. Sci., 2014, 84, 365 CrossRef CAS.
- D. Suetin, I. Shein and A. Ivanovskii, Russ. Chem. Rev., 2010, 79, 611 CrossRef CAS.
- C. Lu, Q. Li, Y. Ma and C. Chen, Phys. Rev. Lett., 2017, 119, 115503 CrossRef PubMed.
- S. Wang, X. Yu, Z. Lin, R. Zhang, D. He, J. Qin, J. Zhu, J. Han, L. Wang, H. Mao, J. Zhang and Y. Zhao, Chem. Mater., 2012, 24, 3023 CrossRef CAS.
- F. Kawamura, H. Yusa and T. Taniguchi, J. Am. Ceram. Soc., 2018, 101, 949 CrossRef CAS.
- D. Choi and P. N. Kumta, J. Am. Ceram. Soc., 2007, 90, 3113 CrossRef CAS.
- A. Zerr, G. Miehe and R. Riedel, Nat. Mater., 2003, 2, 185 CrossRef CAS PubMed.
- E. Gregoryanz, M. Sanloup, J. Badro, G. Fiquet, H. K. Mao and R. J. Hemley, Nat. Mater., 2004, 3, 294 CrossRef CAS PubMed.
- J. Crowhurst, A. Goncharov, B. Sadigh, C. Evans, P. Morrall, J. Ferreira and A. Nelson, Science, 2006, 311, 1275 CrossRef CAS PubMed.
- A. F. Young, C. Sanloup, E. Gregoryanz, S. Scandolo, R. H. Hemley and H. K. Mao, Phys. Rev. Lett., 2006, 96, 155501 CrossRef PubMed.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063 CrossRef CAS.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B, 2010, 82, 094116 CrossRef.
- X. Zhang, Y. Wang, J. Lv, C. Zhu, Q. Li, M. Zhang, Q. Li and Y. Ma, J. Chem. Phys., 2013, 138, 114101 CrossRef PubMed.
- Y. Li, J. Hao, H. Liu, Y. Li and Y. Ma, J. Chem. Phys., 2014, 140, 174712 CrossRef PubMed.
- M. Zhang, H. Liu, Q. Li, B. Gao, Y. Wang, H. Li, C. Chen and Y. Ma, Phys. Rev. Lett., 2015, 114, 015502 CrossRef PubMed.
- L. Zhang, Y. Wang, J. Lv and Y. Ma, Nat. Rev. Mater., 2017, 2, 17005 CrossRef CAS.
- L. Zhu, H. Liu, C. J. Pickard, G. Zou and Y. Ma, Nat. Chem., 2014, 6, 644 CrossRef CAS PubMed.
- X. Yong, H. Liu, M. Wu, Y. Yao, J. S. Tse, R. Dia and C. S. Yoo, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 11110 CrossRef CAS PubMed.
- D. M. Ceperley and B. Alder, Phys. Rev. Lett., 1980, 45, 566 CrossRef CAS.
- J. Ihm, A. Zunger and M. L. Cohen, J. Phys. C: Solid State Phys., 1979, 12, 4409 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B, 1999, 59, 1758 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188 CrossRef.
- A. Togo, F. Oba and I. Tanaka, Phys. Rev. B, 2008, 78, 134106 CrossRef.
- R. Hill, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349 CrossRef.
- X. Guo, L. Li, Z. Liu, D. Yu, J. He, R. Liu, B. Xu, Y. Tian and H. Wang, J. Appl. Phys., 2008, 104, 023503 CrossRef.
- X. Chen, H. Niu, D. Li and Y. Li, Intermetallics, 2011, 19, 1275 CrossRef CAS.
- A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397 CrossRef CAS.
- B. Silvi and A. Savin, Nature, 1994, 371, 683 CrossRef CAS.
- M. Born and R. D. Misra, On the stability of crystal lattices, Cambridge University Press, 1940, vol. 36, p. 466 Search PubMed.
- F. Occelli, D. L. Farber and R. L. Toullec, Nat. Mater., 2003, 2, 151 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2018 |