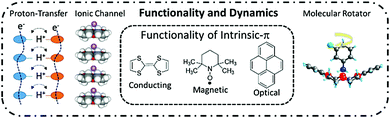
Dynamic molecular assemblies toward a new frontier in materials chemistry

Abstract

The crystal lattice energy of π-molecules is dominated by weak and anisotropic intermolecular interactions ranging in energy from 1 to ∼20 kJ mol⁻¹, which can be tuned by the introduction of specific interaction sites to the parent π-molecular core. In various types of π-molecular crystals, supramolecular approaches using directional hydrogen-bonding, halogen bonding, π-stacking, host–guest, and hydrophobic interactions have been effectively used to achieve lattice dynamics including proton transfer, ionic transport, and molecular rotations in the closest-packing molecular assemblies. Such approaches enable the formation of dynamic multi-functional intrinsic π-electronic materials with electrical conductivity, magnetism, and unique optical responses. Short-range collective proton transfer occurs along intermolecular hydrogen-bonding networks and is correlated with the dipole inversion and ferroelectricity, whereas long-range proton transport is directly associated with bulk protonic conduction. Dynamic proton and ionic transport in the molecular assemblies can be designed for protons via hydrogen bonding and for Li⁺ and/or Na⁺via ionic channels, where the freedom of motion is coupled with the intrinsic π-electronic properties. When the dynamic molecular rotation of the polar structural unit is controllable by an outer electric field, the dipole inversion and dielectric responses of the molecular assemblies are associated with ferroelectricity. Careful design of the polar rotary unit has the potential to create artificial molecular motors or futuristic molecular assembly machines. These dynamic molecular assemblies can be coupled with intrinsic π-electronic functions, offering a new direction in the future of materials chemistry.

---

T. Akutagawa

Tomoyuki Akutagawa received his PhD degree from Kyoto University. He is currently the Professor of Institute of Multidisciplinary Research for Advanced Materials (IMRAM), Tohoku University. His main research is based on physical chemistry, functional material chemistry, supramolecular chemistry such as electrical and ionic conducting, magnetic, fluorescence, ferroelectric, and ferroelastic properties. He is now trying to fabricate new hierarchal systems of functional molecular assemblies.

---

Dynamic molecular assemblies

Both covalent- and ionic-bonds contribute to the interatomic interaction in typical inorganic materials, resulting in higher thermal stability and excellent physical properties compared to those of organic materials.¹ The crystal lattice energy of the organic molecules is dominated by various kinds of intermolecular interactions including electrostatic, charge-transfer, hydrogen-bonding, halogen–halogen, van der Waals (dipole–dipole, dispersive polarization, induced polarization, etc.), and hydrophobic interactions. The different magnitudes of these interactions play an important role in the design of multi-functionalities towards obtaining soft molecular assemblies.² Therefore, one of the advantages of using organic molecular assemblies is their wide variation of possible intermolecular interactions. Relatively strong electrostatic Madelung energy is the most essential aspect of an ionic charge-transfer complex, (Donor^+δ)(Acceptor^−δ), with a magnitude of charge-transfer δ = 1.³ Directional intermolecular hydrogen-bonding interactions have been observed in a large number of molecular assemblies, such as one-dimensional (1D) chains of phthalic and isophtahlic acids,⁴ two-dimensional (2D) layers of squaric acid or trimesic acid,⁵ and three-dimensional (3D) diamond-like networks of tetracarboxylic acid derivatives.⁶ In contrast, weak van der Waals interactions are useful for fabricating flexible and dynamic molecular crystals, such as adamantane and n-alkanes.^7,8 Both the magnitude of energy and the directionality of intermolecular interactions are essential for determining the intrinsic electrical conductivity, magnetism, and optical properties of the fabricated material.⁹ Physical parameters of superconducting and/or ferromagnetic phase transition temperatures of the weakly interacting organic π-molecules are much lower compared to those of strongly interacting inorganic ones.¹⁰ However, the precise design of these weak intermolecular interactions as part of molecular assemblies is useful to fabricate dynamic and soft molecular assembly structures similar to those found in biological systems. For instance, polypeptide chains are obtained through covalent bonding of twenty possible amino acids, and the secondary molecular assembly structures including α-helices and β-sheets are assembled by amide-type N–H⋯O= hydrogen-bonding interactions (Scheme 1).¹¹ Molecular assembly of the secondary structures forms hierarchical ternary structures through weak van der Waals interactions, which allows for the plasticity and reconstructivity of biological system at room temperature.¹¹ Since biological molecular assemblies are constructed by different magnitudes of intermolecular interactions from covalent bonds, hydrogen-bonding, to van der Waals interactions, reversible association and dissociation processes are easily achieved around room-temperature energy (k_BT) to realize self-healing and effective enzyme reaction cycles. Dynamic and elastic molecular assemblies have been well utilized and organized to create dynamically ordered biological molecular assemblies. However, some organic molecules and virus crystals are obtained in the static state with a large minimum free energy. If dynamic ordering molecular assemblies can be freely designed and applied in molecular assembly devices, new kinds of molecular machines will be possible for use in highly efficient energy conversion systems.¹² Currently, there are insufficient design strategies available to fabricate such complex and futuristic molecular assembly machines.

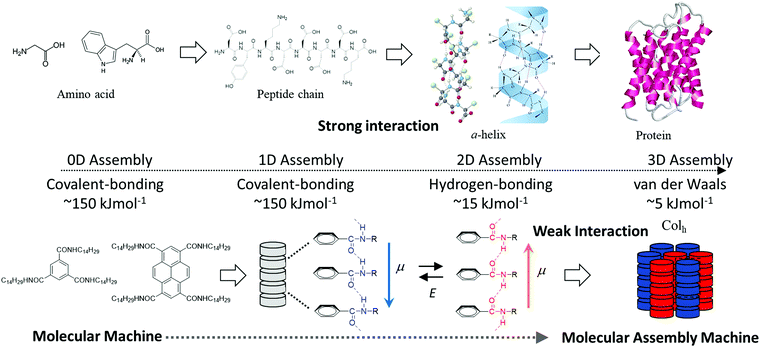Scheme 1 Hierarchal energy scale of intermolecular interactions in protein and molecular assembly machines.

Various types of dynamics including proton transfer, ionic motion, and molecular rotation have been examined in molecular assembly structures. For instance, cooperative intermolecular proton-transfer of a carboxylic acid dimer,¹³ rotation of methyl (–CH₃) groups in benzene derivatives,¹⁴ in-plane rotation of aromatic π-molecules,¹⁵ rotator phases of spherical molecules of C₆₀,¹⁶ and adamantane (C₁₀H₁₆)¹⁷ have been evaluated by the spectroscopic techniques and X-ray inelastic scattering measurements.¹⁸ These solid-state dynamic behaviors occur via thermally activated random Brownian motion. Although the motional freedoms of rotation frequency and symmetry can be controlled by the molecular design and crystal engineering, the control of unidirectional rotary motion in a clockwise or anti-clockwise direction has yet to be achieved in the molecular assemblies confounding the production of an artificial molecular motor. Thermally activated Brownian motions, such as the rotation of –CH₃ groups and proton transfer in hydrogen-bonding systems, are observed as stochastic phenomena with an equal probability for clockwise and anti-clockwise rotations. These random molecular motions can never be transformed into a work function according to the second law of thermodynamics.¹⁹ A molecular motor and a proton pump cooperatively operate the biological molecular system in ATPase,²⁰ where the unidirectional molecular motor activates the proton pump to catalyze ATP production from ADP with high energy conversion efficiency of approximately 100%. The unidirectional biological molecular motor has a completely different working principle compared to an artificial random molecular rotator. Therefore, the design of the dynamic molecular environment in the molecular assemblies must be carefully controlled to fabricate dynamic and functional molecular assembly systems, which can be used to mimic biological molecular machines. From this perspective, we discuss the dynamic behaviors of protons, ions, and molecules in π-functional molecular assemblies (Fig. 1).

Fig. 1 Molecular assemblies including intrinsic-π functions such as electrical conducting, magnetic, and optical properties coupled with the dynamic functions of proton transfer, ion channel, and molecular motion.

Proton dynamics in molecular assemblies

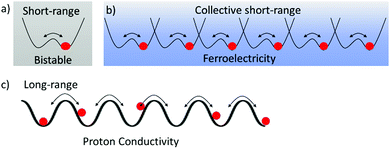
The mass of a proton is an approximately one thousand times larger than that of an electron, resulting in a proton mobility one thousand times lower than that of electrons in the molecular assemblies. Proton transfer in hydrogen-bonding structures plays an essential role in realizing the biological functions such as proton pumping, electron transport coupled with the 2H⁺–2e⁻ reaction of p-benzoquinone (BQ)–hydroquinone (H2Q), redox pairs of ubiquinone, and photo-isomerization of the retinal–retinol tautomer in optic nerve of rhodopsin.²¹ In biological systems, both proton and electron transfer have been cleverly used in energy transfer processes and for information transmittance. In solid state physics, the cooperative proton and electron transfer phenomena in hydrogen-bonding charge transfer complexes of quinhydrone (BQ)(H2Q) between the electron acceptor, BQ, and the electron donor, H2Q, indicated an interesting phase transition behavior to a semiquinone neutral radical state, HQ˙, under high pressure.²² Proton transfer in the organic π-molecules has the potential to form new dynamic molecular assemblies.²³

Short-range proton transfer in hydrogen-bonding molecular assemblies is followed by a double-wall potential energy curve creating bi-stable energy minima for the protonic coordinate, whereas the long-range transfer is observed in hydrogen-bonding network structures (Fig. 2).²⁴ Short-range cooperative proton-transfer along the 1D hydrogen-bonding chain generates a macro dipole moment and its inversion by the outer electric field can result in a ferroelectric response (Fig. 2b). For instance, thermal fluctuations of proton arrangements in the 1D N–H⋯N hydrogen-bonding chains of (HDABCO⁺)·ClO₄⁻ and (HDABCO⁺)·BF₄⁻ crystals were frozen at 377 and 378 K, respectively, resulting in a high temperature paraelectric and low temperature ferroelectric phase transition (HDABCO⁺ is mono-protonated 1,4-diazabicyclo[2.2.2]octane).²⁵ Lower thermal energy (k_BT) and smaller energy barrier (ΔE) of the double-wall potential energy curve results in proton ordering in the 1D hydrogen-bonding chain according to the ice rule. Here, the ice rule indicates that the uniformly monoprotonated HDABCO⁺ arrangement in the 1D chain is much more stable than the formation of disproportionation states of diprotonated H₂DABCO²⁺ and neutral DABCO⁰ species within the 1D N–H⋯N hydrogen-bonding chain. In this assembly, each proton is arranged in the same orientation along the 1D chain to generate the macro dipole moment with a ferroelectric response.²⁶

Fig. 2 Short-range and long-range proton transfer and potential energy curves for the proton coordinates in the molecular assemblies. (a) Bi-stable short-range proton transfer for switching behavior. (b) Collective short-range proton transfer in a hydrogen-bonding network for the ferroelectric–paraelectric phase transition. (c) Long-range proton transfer for protonic conductivity along a hydrogen-bonding network.

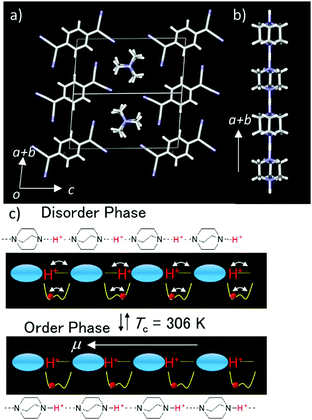
The thermally activated order–disorder phase transition of proton orientation in the 1D hydrogen-bonding chain is closely associated with its ferroelectric–paraelectric phase transition behavior, which can be also coupled with the intrinsic electrical conductivity (Fig. 3). The highly electrical conducting anion radical salt (HDABCO⁺)₂(TCNQ)₃ has been used as an organic semiconductor with dielectric switching behavior (TCNQ is 7,7,8,8-tetracyano-p-quinodimethane). The dielectric phase transition of 1D hydrogen-bonding of the (HDABCO⁺)_∞ chain from the low temperature ferroelectric to high-temperature paraelectric states affects its electrical conductivity on the π-column of partially reduced TCNQ.²⁷ The 1D N–H⁺⋯N hydrogen-bonding chains can elongate along the a + b axis parallel to the electrical conducting π-stack of TCNQ (Fig. 3a and b). The symmetrical potential energy curve of the N–H⁺⋯N hydrogen-bonding chain determines the collective motion of the protons according to the temperature. At temperatures above 306 K, the thermally activated fluctuation of protons occurs and cancels the macro dipole moment along the 1D (N–H⁺⋯N)_∞ chain in a paraelectric state (Fig. 3c). When the thermal energy (k_BT) is smaller than the potential energy barrier, below 306 K (Fig. 3c), each proton in the 1D (N–H⁺⋯N)_∞ chain was fixed along one direction according to the ice rule to generate a macro dipole moment with a ferroelectric state.

Fig. 3 Dynamic short-range collective proton transfer and dielectric switching in the organic semiconductor (HDABCO⁺)₂(TCNQ)₃. (a) Unit cell viewed along the 1D (N–H⁺⋯N)_∞ hydrogen-bonding chain and electrical conducting π-column of TCNQ. (b) High temperature 1D (N–H⁺⋯N)_∞ hydrogen-bonding chain of HDABCO⁺ cations along the a + b axis. Schematic potential energy curves of the N–H⁺⋯N hydrogen-bonding chain (c) at the high temperature paraelectric disordered phase (upper) and at the low temperature ordered ferroelectric phase (lower) for the proton orientation.

Recently, new ferroelectric–paraelectric phase transition materials coupled with intermolecular proton transfer have been examined using hydrogen-bonding π-molecular crystals such as croconic acid and 5,6-dichloro-2-benzoimidazole.^28,29 In these materials the remnant polarization (P_r) in the polarization–electric field (P–E) curves was reached at approximately 22 and 10 μC cm⁻², respectively,^28,29 similar to that of typical inorganic ferroelectrics of BaTiO₃ crystals (P_r ∼ 26 μC cm⁻²). The order–disorder phase transition temperature of these hydrogen-bonding ferroelectrics was observed at relatively high temperature, which is potentially useful for use in ferroelectric random-access memory devices.

The long-range proton-transfer system along the hydrogen-bonding networks achieves proton conduction instead of a ferroelectric phase transition material (Fig. 2c). However, the hydrogen-bonding ferroelectrics and proton conductors are related. Dynamic and highly mobile hydrogen-bonding networks are essential to design of proton conducting materials for applications in fuel cells. High protonic mobility, larger than 10⁻³ cm² V⁻¹ s⁻¹, in the solid state is challenging to reach, but is required for superprotonic conductors for use in light-weight and low-cost fuel cells.³⁰

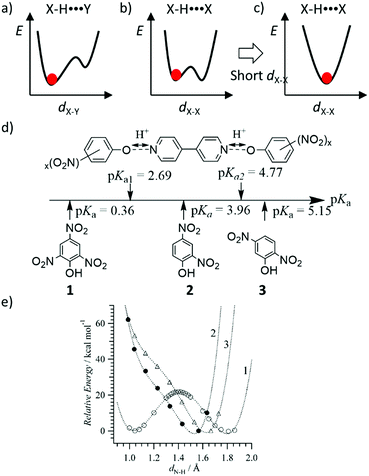
The shape of the double-wall potential energy curve for the proton coordinate is useful for understanding dynamic proton transfer phenomena (Fig. 4). Hetero-type X–H⋯Y intermolecular hydrogen-bonding interactions, such as N–H⋯O and O–H⋯N, generate an asymmetrical potential energy curve for the proton coordinate (Fig. 4a).²⁴ Conversely, homo-type X–H⋯X hydrogen-bonding interactions, such as O–H⋯O and N–H⋯N, create a symmetrical double-wall potential energy curve, which is suitable for intermolecular proton-transfer (Fig. 4b).²⁴ In addition, the magnitude of the potential energy barrier, ΔE, is an important parameter governing proton-transfer, where strong hydrogen-bonding interactions with short X⋯X distances (d_X–X) decrease the magnitude of ΔE. A relatively strong hydrogen-bonding interaction was observed at d_O–O < 2.5 Å in the O–H⋯O hydrogen-bonding structure, which shows a single minimum potential energy curve in the absence of intermolecular proton-transfer (Fig. 4c).³¹ In the single minimum potential energy curve, the order–disorder phase transition of the protonic orientation should be completely suppressed. The quantum paraelectric state, arising due to the quantum protonic frustration, was observed in the low temperature phase in the absence of the protonic ordering ground state.³² Lowering in the ΔE of the double-wall potential energy curve is favorable for intermolecular proton transfer and order–disorder phase transition at relatively low temperatures. In the ferroelectric phase, the coercive electric field (E_th) is also decreased by low ΔE caused by lowering the dipole inversion energy, whereas the elongation of the intermolecular hydrogen-bonding distance increases the dipole moment, μ, and P_r.

Fig. 4 Controlling the hydrogen-bonding potential energy curves. (a) Asymmetrical potential energy curve of hetero-type X–H⋯Y and (b) symmetrical potential energy curve of homo-type X–H⋯X hydrogen-bonding structures. (c) Single minimum potential energy cure of the strong homo-type hydrogen-bonding structure. (d) Brønsted acid–base approach for the intermolecular N–H⋯O hydrogen-bonding system of (4,4′-bipyridine)(polynitorophenol)₂ complexes to control the potential energy curves. (e) Relative energy vs. d_N–H in the theoretical potential energy curves of proton-transferred ionic (4,4′-bipyridinium²⁺)(picrate⁻)₂ (1), (4,4′-bipyridine)(2,4-dinitrophenol)₂ (2), and (4,4′-bipyridine)(2,5-dinitrophenol)₂ (3) complexes.

The potential energy curve for the intermolecular hydrogen-bonding structure was designed by considering the acid dissociation constant (pK_a) of the proton-donor (HD) and proton-acceptor (A) in the hydrogen-bonding D–H⋯A system. Fig. 4d and e show the theoretical potential energy curves at relative energy vs. d_N–H of the proton transferred ionic (4,4′-bipyridinium²⁺)(picrate⁻)₂ (1), neutral (4,4′-bipyridine)(2,4-dinitrophenol)₂ (2), and neutral (4,4′-bipyridine)(2,5-dinitrophenol)₂ (3) complexes. The asymmetrical potential energy curves of hetero-type N–H⋯O hydrogen-bonding structure were observed in neutral hydrogen-bonding 2 and 3 complexes, whereas the symmetrical potential energy curve was obtained in the proton-transferred ionic 1 complex. Although the potential energy barrier at approximately 20 kJ mol⁻¹ in 1 was higher than the energy at room temperature (k_BT ∼ 2.5 kJ mol⁻¹), the application of sufficient thermal energy could induce the phase transition from the ionic to neutral complexes according to the bi-stable potential energy curve (Fig. 4e). In H₂O, the difference in pK_a values between proton donor, HD, and proton acceptor, A, molecules; ΔpK_a = pK_a(HD) − pK_a(HA⁺), becomes an indicator that can be used to evaluate the possibility of proton transfer between the neutral hydrogen-bonding (D–H⋯A) and ionic proton transferred (D⁻⋯HA⁺) states.³⁴ When ΔpK_a > 0, the proton transfer reaction follows the general guidelines of a Brønsted acid–base reaction. In the solid state, although a simple relationship for the neutral-ionic boundary at approximately ΔpK_a ∼ 0 has not been observed in acid–base binary molecular complexes, a design strategy based on ΔpK_a value has become a useful parameter to estimate the proton transfer state of molecular assemblies. The binary molecular complexes formed between polynitrophenol (DH) and aniline derivatives (A) indicate a neutral-ionic boundary of ΔpK_a ∼ ±1 between the neutral (DH)(A) molecular complex (ΔpK_a > ±1) and the proton transferred ionic (D⁻)(HA⁺) complex (ΔpK_a < ±1) (Fig. 5). In this system, the electrostatic Madelung energy in the latter ionic complex shifts the boundary condition to a pK_a of approximately 0.³³ Interestingly, several ionic binary molecular complexes of (D⁻)(HA⁺) near the neutral-ionic boundary indicated a phase transition between low temperature (D⁻)(HA⁺) and high temperature (HD)(A) forms by increasing the temperature and/or applying pressure. For instance, the complex isomerization from the ionic yellow (o-iodoanilinium⁻)(picrate⁺) to neutral red (o-iodoaniline)(picric acid) complex was observed during the thermally activated intermolecular proton transfer in the solid state (Fig. 5b).³⁵ Another important design aspect for the physical function of the materials is the crystal symmetry. In the dynamic phase transition system, the low symmetry polar space groups have been observed at low temperature phase, which has potential to show ferroelectricity,³⁴ second harmonic generation (SHG), and piezoelectricity. Based on a structural database, the intermolecular hydrogen-bonding patterns and crystal symmetry can be used for discovering new ferroelectric molecular crystals. In near future, AI technology will be used to find potential ferroelectric or SHG materials among a vast crystal structural database.

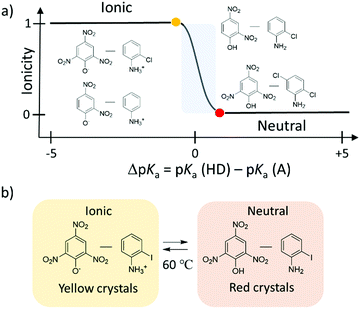Fig. 5 Formation of the neutral (HA)(B) and ionic (A⁻)(HB⁺) hydrogen-bonding binary molecular complexes through the combination of polynitrophenol (HA) and aniline (B) derivatives. (a) A design strategy where ΔpK_a = pK_a(HD) − pK_a(HA⁺) is useful in determining the type of binary hydrogen-bonding molecular complexes (ionic or neutral). (b) Complex isomerization from ionic yellow (o-iodoanilinium⁻)(picrate⁺) to neutral red (o-iodoaniline)(picric acid) complexes by thermally activated intermolecular proton transfer in the solid state.³⁵

Several scientific challenges must be solved for hydrogen-bonding molecular assemblies to realize designable gated- and unidirectional proton transport (pumping). Since the hetero-type X–H⋯Y hydrogen-bonding structure has an asymmetrical potential energy curve for the proton coordinate, the formation of Ratchet-type asymmetrical potential energy curves would likely achieve unidirectional molecular rotation in the biological motor (Fig. 6). The introduction of asymmetry into the thermally activated Brownian motion under the application of periodic bias is a proposed mechanism by which to realize unidirectional protonic transport along the (X–H⋯Y)_∞ hydrogen-bonding chain. In addition, the polarized proton arrangement in the protonic channel provides an asymmetric solid-state environment to align each dipole moment of H₂O molecules for unidirectional H₂O transport like in the water transporting protein aquaporin.³⁶ The artificial design of a unidirectional H₂O transport channel is an interesting concept for the field of molecular assembly machinery.

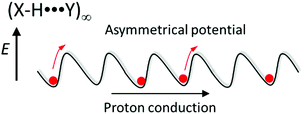Fig. 6 Asymmetrical hydrogen-bonding Ratchet-type potential energy curve for unidirectional proton transport along a hetero-type (X–H⋯Y)_∞ hydrogen-bonding chain.

Ion dynamics in molecular assemblies

In the biological cellular membrane, selective and passive ion transport channels for Na⁺, K⁺, and Ca²⁺ in lipid bilayers have been observed by concentration differences and electrical gradients between the inner cytosol and the outer matrix.³⁷ ATP hydrolysis is coupled with the ionic transport of three Na⁺ ions from the inner to outer side of the membrane and two K⁺ ions from the outer matrix to the inner membrane side in the Na⁺/K⁺ pump (Fig. 7).³⁷ The ionic pump and channel are active and passive transport systems, respectively, and the ionic flow through the cell membrane follows the Nernst's equation through the activation voltage for the nervous system to transmit electrical signal and information. Artificial ionic channels have been studied in the fields of the host–guest and supramolecular chemistry using a number of artificial pore molecules including crown ethers and calixarenes.^38,39 A variety of artificial ionic channel molecules have been designed and synthesized,⁴⁰ some of which have been introduced into artificial lipid bilayers to fabricate the ionic transport. Unfortunately, no ideal artificial ionic transport membrane has been synthesized with similar properties as its biological counterpart for possible applications in ionic devices. Although the ionic channels with controllable pore size for the selective ion transport have been developed, further control in the assembly process for independent Na⁺ and K⁺ channels in artificial lipid bilayers is still being researched.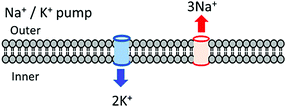

Fig. 7 Biological ionic channels for selective, directional, and coupled 2 Na⁺ and 3 K⁺ ion transport through the cell membrane.

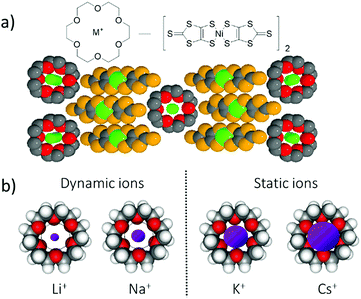
For a multi-functional π-molecular system, the coexistence of uniform stacks of crown ethers and conducting metal-coordinated π-molecules of [Ni(dmit)₂] have been reported to form hybrid ionic and electronic transport system (dmit²⁻ is 2-thioxo-1,3-dithiole-4,5-dithiolate).⁴¹ The partially oxidized π-stacking column of [Ni(dmit)₂] forms a metallic electrical conducting π-band, whereas the ionic channel of the cationic M⁺_x(crown ether) forms a counter cation structure to compensate for the total charge of the crystals. Interestingly, the change in ionic size from Li⁺, Na⁺, K⁺, Rb⁺, to Cs⁺ is captured by the central cavity of the crown ether, affecting the periodic potential for the conduction of electrons on the π-stack of [Ni(dmit)₂] (Fig. 8).⁴² The dynamic motion of small Li⁺ and Na⁺ ions in the ionic channels occurred in the cavity of the [18]crown-6 ether, and Li⁺ conduction was observed at approximately 10⁻⁶ S cm⁻¹ at room temperature based on the AC impedance measurements using an electron blocking electrode.⁴¹ Conversely, relatively large K⁺ and Rb⁺ ions were completely captured in the central cavity of [18]crown-6, forming static cation structures.⁴² The large Cs⁺ ion was excluded from the central cavity of [18]crown-6 and was not allowed to pass through (Fig. 8b). The conduction electrons on the π-stack were modulated by the electrostatic potential of the cations in the solid state according to their motional freedom. The static Cs⁺ cations generated periodic electrostatic potential for the conduction of electrons, resulting in relatively high electrical conduction. However, dynamic ions such as Li⁺ generated a dynamic electrostatic potential for the conduction of electrons on the π-stack, which diffused the periodic potential and became a random pinning potential at low temperatures.

Fig. 8 Dynamic (M⁺ = Li⁺ and Na⁺) and static (M⁺ = K⁺ and Cs⁺) ionic channels in conducting M⁺_x([18]crown-6)[Ni(dmit)₂]₂ salts. (a) Molecular structures and packing structure. The motional freedom of the cations affected the potential for the conduction electrons on the π-stack of partially oxidized [Ni(dmit)₂]. (b) Dynamic and static ion environments were observed according to the size of the alkali metal ions (Li⁺, Na⁺, K⁺, and Cs⁺) and cavity size of the [18]crown-6 ether.

In the dynamic ionic system, several challenges were overcome similar to those in the dynamic protonic system. For instance, the gated- and unidirectional ionic transports must be artificially realized in the molecular assemblies to be used for information transmittance with different kinds of ions instead of electrons. The fabrication of such ionic transport technology is an aspirational research target in the near future. The question remains: how to design such complex molecular assembly structures including different types of gated- and active-ionic channels? The solution of this question is closely related to the control of hierarchical molecular assemblies based on weak intermolecular interactions. The double-wall potential energy curve for the ionic coordinate is useful for controlling the short- and long-range dynamic ionic motions to fabricate the atomic displacement ferroelectrics and ionic conductors. For instance, the atomic displacements in the inorganic ferroelectrics of BaTiO₃ indicated the dipole inversion in their P–E curves, where the shape of double-wall potential energy curve for the ionic coordinate is essential in determining the possible ferroelectric functions.⁴³ The network type long-range assembly structure for the ionic arrangement is also important for ionic conductors, where various ions have the potential to possess motional freedom within the molecular assemblies. Ions with different sizes, charges, and spin states can be applied for the future ionic devices and information technology based on ionic motion.

Dynamic molecular motion in molecular assemblies

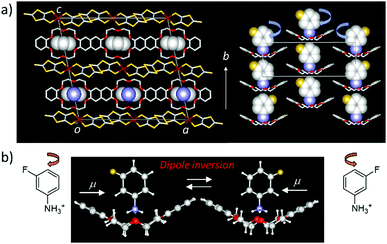
Large amplitude molecular motions are usually restricted in close-packed molecular assemblies and dynamic crystalline space in the solid state. However, thermally activated molecular rotations have been observed in spherical molecules such as cyclohexanol, triethylenediamine, C₆₀, and adamantane, where the positions of each molecule are kept in the crystal lattice, called the plastic crystal or rotator phase.¹⁸ In the liquid crystalline phase, only the molecular orientation is maintained in the dynamic molecular assemblies in the absence of periodicity for each molecular gravity, indicating fluidic behavior.⁴⁴ In the plastic crystalline state, the average molecular packing structure of the thermally activated rotary molecules can be determined by single crystal X-ray structural analysis. The low temperature ordered crystalline phase could be transformed to a high temperature disordered plastic crystalline rotator phase, where the order–disorder phase transition temperature is determined by the magnitude of the intermolecular interaction strength. For instance, the order–disorder phase transition temperatures of C₆₀ and adamantane crystals were 260 and 208 K,^45,46 respectively, suggesting stronger intermolecular π–π interactions in the C₆₀ crystals compared the van der Waals interactions in the adamantane crystals. Molecular symmetry is also directly associated with the rotational anisotropy, ranging from 1D uniaxial, 2D bi-axial, to 3D isotropic rotation. The thermally activated rotary motion in the plastic crystalline state result from random Brownian motion, which is completely opposite to the unidirectional rotation in biological molecular motors. A significant difference between the molecular motor and rotator is the possible production of a work function from the molecular motion. The second law of thermodynamics prohibits the extraction of work from random motion. Although a variety of molecular rotary modes can be observed in molecular assemblies in the plastic crystalline and liquid crystalline states, these motional freedoms are not correlated to the physical responses of functional materials. For instance, the order–disorder phase transition of adamantane crystals is insensitive to physical responses, and the thermal conductivity (κ) of C₆₀ crystals was only slightly decreased from 0.5 W m⁻¹ K⁻¹ in its low temperature ordered phase to 0.4 W m⁻¹ K⁻¹ in its high temperature disorder phase due to the melting of crystal lattice.⁴⁷ Since the magnitude of κ is mainly influenced by the lattice vibration of the crystal (phonon), the disordered molecular orientation affects its thermal transport properties.

Dielectric responses have been observed arising from various types of molecular motion of polar structural units in the molecular assemblies. The two-fold 180° flip-flop motion of the anilinium (Ani⁺) cation along the C–NH₃⁺ axis has been observed in the solid state ²H NMR spectra of Ani⁺([18]crown-6)[Ni(dmit)₂] crystals. The thermally activated molecular motion of Ani⁺ cation was directly observed with a 6 MHz at room temperature.⁴⁸ However, this flip-flop motion in the molecular assemblies was insensitive to dielectric spectroscopy due to the small effective change in the dipole moment. When the measuring frequency of the dielectric spectra, a Debye-type relaxation process is often observed at the frequency dependent dielectric peaks.⁴⁹ The motion of the polar rotary unit of m-fluoroanilinium (m-FAni⁺) cation along the C–NH₃⁺ axis was designed to respond to the dielectric spectra due to the change in dipole moment of the m-FAni⁺(dibenzo[18]crown-6)[Ni(dmit)₂] crystals (Fig. 9), which clearly showed the temperature- and frequency-dependence dielectric responses.⁵⁰ Thermally activated flip-flop motion of the polar m-FAni⁺ cation in the crystals changes the direction of the dipole moment, indicating the ordered ferroelectric–disordered paraelectric phase transition at approximately 350 K. In the low temperature ordered ferroelectric phase below 350 K, the orientation of m-FAni⁺ cations can be controlled by the application of an outer electric field. Conversely, thermally activated random orientation of the dipole moments of polar m-FAni⁺ cations occurs in the high-temperature disordered paraelectric phase. The rotational freedom of the polar structural units in the molecular assemblies can be correlated with the macro physical property of ferroelectricity.

Fig. 9 Two-fold flip-flop motion of m-FAni⁺ cations along the C–NH₃⁺ axis in monovalent [Ni(dmit)₂] crystals. (a) Unit cell and supramolecular rotator layer in m-FAni⁺(dibenzo[18]crown-6)[Ni(dmit)₂] crystals. (b) The motional freedom of polar m-FAni⁺ cations is sensitive to the dielectric response and resulted in the phase transition from the low temperature ferroelectric to the high temperature paraelectric states.

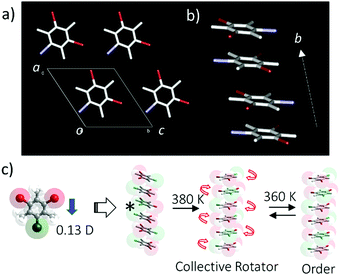
Another interesting in-plane molecular rotary system has been observed in halogen-substituted mesitylene crystals such as dibromoiodomesitylene (DBIM), which has an in-plane permanent dipole moment (Fig. 10).⁵¹ The π-stacking structure of DBIM has been observed in the orientationally disordered arrangement of the iodine position in single crystal X-ray structural analysis. The dynamic in-plane molecular rotation of the polar DBIM molecules is thermally activated at the temperatures above 380 K, where motion can be observed by polarized optical microscope, thermal analysis, and dielectric spectral measurements. The high temperature disordered paraelectric phase transformed to the low temperature ordered antiferroelectric phase, where each DBIM molecule adopts an anti-parallel dipole arrangement to cancel the macro dipole moments in the antiferroelectric state. Interestingly, effective I⋯I interaction within the π-stacking column was correlated with each in-plane molecular rotation,⁵² resulting in three-fold cooperative in-plane molecular rotation within the π-stacking column. However, such collective rotation independently occurred in the crystal, resulting in overall random motion.

Fig. 10 The in-plane collective molecular rotation by intermolecular I⋯I interaction within the π-stacking column. (a) Unit cell of DBIM viewed along the b axis. (b) The π-stacking column of DBIM along the b axis with the orientationally disordered iodine position. (c) Schematic model of the collective molecular rotation within the π-stacking column. Each collective column showed thermally activated independent rotations, which cancelled the overall macro dipole moment.

Molecular diffusion of neurotransmitters such as glutamic acid, adrenaline, and acetylcholine play an important role in information transmission in neurons.⁵³ In general, this type of molecular diffusion is usually suppressed in molecular assemblies. However, thermally activated molecular rotations or fluctuation have been observed even in close-packing molecular assembly structures. High-efficiency energy conversion system similar to the biological molecular motors would benefit from this type of motion. Such a molecular mechanical device has not yet been fabricated and is a near-term goal of many researchers. Chiral molecular rotational environments bearing S- and R-molecules can generate asymmetrical potential for the molecular rotations, which may fulfil one of the requirements for the fabrication of an artificial unidirectional molecular motor. Directional transport and work under Brownian motion have been developed to explain various fluctuation driven transport modes such as stochastic pumping, which govern transport in Brownian motors and ratchets.⁵⁴ It has been proposed a numerical algorithm for calculation of quantized directed motion of a stochastic system of interacting particles induced by periodic changes of control parameters on the graph of microstates.⁵⁵ In addition, some theoretical aspects of motor-protein dynamics are presented in the light of current experimental methods that enable the measurement of the biochemical and biomechanical properties on a single-molecule basis.⁵⁶ These theoretical approach enable us to design new dynamic molecular assemblies with possible works. After the success of fabricating the initial artificial molecular motor, a hybrid molecular assembly including different functional units such as motors, protonic pumps, ionic pumps, and catalytic reactors could be simultaneously assembled. Studies towards this goal are some of the most significant and worthwhile efforts for the development of new material chemistry frontiers.

Summary

Dynamic molecular assemblies allowing motional freedom of protons, ions, and molecules were discussed herein in terms of proton transfer, proton conduction, ferroelectrics, ionic channels, and molecular rotators. The potential energy curves for the motional freedom are tunable in the close-packing molecular assemblies using a supramolecular approach. Various future research targets such as the artificial proton pumps, selective ionic channels, and gated channels, already exist as biological molecular assemblies. Unfortunately, fabrication of these functional dynamic molecular assemblies remains a challenge given the present scientific and technological knowledge. Simultaneous operation of each function in the molecular assembly is an important milestone to realize molecular assembly machines similar to those present throughout nature. Material chemistry and physics based on static crystal lattices have established the parameters of intrinsic π-molecular materials. Dynamic molecular assemblies, similar to the ones found in biological systems, have the potential for new functionality. Properties of intrinsic π-molecules such as electrical conductivity, magnetism, and optical properties can be coupled with dynamic molecular assemblies for proton transfer, proton pumps, active ionic channels, and molecular rotation in the near future. Highly ordered dynamic functionally molecular assemblies could be further assembled with each other, which will open a new field of futuristic molecular assembly devices. Control of each molecular assembly and its suitable processing technology are crucial for the next stage in the development of this material chemistry frontier.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by a Grant-in-Aid for Scientific Research on Innovative Areas “π-Figuration” (JP26102007), KAKENHI Kibankenkyu (B) (JP15H03791), and “Dynamic Alliance for Open Innovation Bridging Human, Environment and Materials” from MEXT.

Notes and references

1. (a) F. A. Cotton, G. Wilkinson, C. A. Murillo and M. Bochmann, Advanced Inorganic Chemistry, John Wiley & Sons, New York, 6th edn, 1999; (b) I. D. Brown, The Chemical Bond in Inorganic Chemistry. The Bond Valence Model, Oxford University Press, New York, 2002.
2. (a) A. I. Kitaigorodsky, Molecular Crystals and Molecules, Academic Press, New York, 1973; (b) F. H. Herbstein, Crystalline Molecular Complexes and Compounds, Structures and Principles, Oxford Scientific Publication, 2005; (c) J. D. Dunitz and A. Gavezzotti, Chem. Soc. Rev., 2009, 38, 2622–2633; (d) A. Gavezzotti, Molecular Aggregation: Structure analysis and molecular simulation of crystals and liquids, Oxford Scientific Publication, 2010.
3. (a) H. M. Mcconnel, B. M. Hoffman and R. M. Metzger, Proc. Natl. Acad. Sci. U. S. A., 1965, 53, 44–50; (b) J. B. Torrance and B. D. Silverman, Phys. Rev. B: Solid State, 1977, 15, 788–801.
4. (a) Y. M. Bailey and C. J. Brown, Acta Crystallogr., 1967, 22, 387–391; (b) J. L. Derissen, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1973, 30, 2764–2765; (c) B. R. Alcala and S. Martinez-Carrera, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 1671–1677.
5. (a) D. J. Duchamp and R. E. Marsha, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1969, 25, 5–19; (b) D. Semmingsen, Acta Chem. Scand., 1973, 23, 3961–3972; (c) F. J. Hollander, D. Semmingsen and T. F. Koetzle, J. Chem. Phys., 1977, 67, 4825–4831.
6. (a) O. Ermer, J. Am. Chem. Soc., 1988, 110, 3141–3154; (b) P. Holý, J. Závada, I. Císařová and J. Podlaha, Angew. Chem., Int. Ed., 1999, 38, 381–383.
7. (a) C. E. Nordman and D. L. Schmitkons, Acta Crystallogr., 1965, 18, 764–767; (b) J. Donohue and S. H. Goodman, Acta Crystallogr., 1967, 22, 352–354.
8. (a) G. Ungar, J. Phys. Chem., 1983, 87, 689–695; (b) R. Boese, H.-C. Weiss and D. Bläser, Angew. Chem., Int. Ed., 1999, 38, 981–992.
9. (a) J. K. Whitesell, Organised Molecular Assemblies in the Solid State, John Wiley & Sons, New York, 1999; (b) J. Fraxedas, Molecular Organic Materials. From Molecules to Crystalline Solids, Cambridge University Press, 2006; (c) G. Saito and Y. Yoshida, Bull. Chem. Soc. Jpn., 2007, 80, 1–137.
10. (a) J. M. Williams, J. R. Ferraro, R. J. Thorn, K. D. Carlson, U. Geiser, H. H. Wang, A. M. Kini and M.-H. Whangbo, Organic Superconductors, ed. R. N. Grimes, Prentice-Hall, New Jersey, 1992; (b) T. Ishiguro, K. Yamaji and G. Saito, Organic Superconductors, ed. M. Cardona, P. Fulde, K. von Klitzing and H.-J. Queisser, Springer-Verlag, Berlin, 2nd edn, 1998; (c) J. S. Miller, A. J. Epstein and W. M. Reief, Science, 1988, 240, 40–47; (d) J. S. Miller, Mater. Today, 2014, 17, 224–235.
11. D. Whitford, Protein. Structure and Function, John Wiley & Sons, NJ, 2005.
12. (a) M. Piccolino, Nat. Rev. Mol. Cell Biol., 2000, 1, 149–152; (b) P. D. Boyer, Annu. Rev. Biochem., 1997, 66, 717–749; (c) A. Grakoui, S. K. Bromley, C. Sumen, M. M. Davis, A. S. Shaw, P. M. Allen and M. L. Dustin, Science, 1999, 285, 221–227.
13. (a) S. Nagaoka, T. Terao, F. Imashiro, A. Saika, N. Hirota and S. Hayashi, J. Chem. Phys., 1983, 79, 4694–4703; (b) G. Feng, L. B. Favero, A. Maris, A. Vigorito, W. Caminati and R. Meyer, J. Am. Chem. Soc., 2012, 134, 19281–19286; (c) C. C. Wilson and A. E. Goeta, Angew. Chem., Int. Ed., 2004, 43, 2095–2099.
14. (a) J. J. Ruch, J. Chem. Phys., 1967, 47, 3936–3943; (b) W. C. Hamilton, J. W. Edmonds and A. Tippe, Discuss. Faraday Soc., 1969, 48, 192–204; (c) M. Prager, H. Grimma and I. Natkaniec, Phys. Chem. Chem. Phys., 2005, 7, 2587–2593.
15. T. Atake, H. Gyoten and H. J. Chihara, Chem. Phys., 1982, 76, 5535–5540.
16. R. D. Johnson, C. S. Yannoni, H. C. Dorn, J. R. Salem and D. S. Bethune, Science, 1992, 255, 1235–1238.
17. S.-S. Chang and E. F. Westrum Jr., J. Phys. Chem., 1960, 64, 1547–1551.
18. J. N. Sherwood, The Plastically Crystalline State, John Wiley & Sons, Chichester, 1979.
19. (a) R. D. Astumian, Science, 1997, 276, 917–922; (b) R. Yasuda, H. Noji, K. Kinosita Jr. and M. Yoshida, Cell, 1998, 93, 1117–1124.
20. (a) B. Albert, D. Bray, A. Johnson, J. Lewis, M. Raff, K. Roberts and P. Walter, Molecular Biology of the Cell, Garland Publishing, New York, 1994; (b) L. Stryer, Biochemistry, Freeman, New York, 1995.
21. (a) R. E. Blankenship, Anoxygenic Photosynthetic Bacteria. Advances in Photosynthesis, Kluwer, New York, 1996, vol. 2; (b) D. R. Ort, Oxygenic Photosynthesis. The Light Reactions. Advances in Photosynthesis, Kluwer, New York, 1996, vol. 4.
22. T. Mitani, G. Saito and H. Urayama, Phys. Rev. Lett., 1988, 60, 2299–2302.
23. (a) T. Akutagawa and G. Saito, Bull. Chem. Soc. Jpn., 1995, 68, 1753; (b) T. Akutagawa, G. Saito, M. Kusunoki and K. Sakaguchi, Bull. Chem. Soc. Jpn., 1996, 69, 2487; (c) T. Isono, H. Kamo, A. Ueda, K. Takahashi, A. Nakao, R. Kumai, H. Nakao, K. Kobayashi, Y. Murakami and H. Mori, Nat. Commun., 2013, 4, 2352; (d) A. Ueda, S. Yamada, T. Isono, H. Kamo, A. Nakao, R. Kumai, H. Nakao, Y. Murakami, K. Yamamoto, Y. Nishio and H. Mori, J. Am. Chem. Soc., 2014, 136, 12184–12192.
24. (a) G. A. Jeffrey, An Introduction to Hydrogen Bonding, Oxford University Press, 1997; (b) T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48–76; (c) G. Gilli and P. Gilli, The Nature of the Hydrogen Bond. Outline of a Comprehensive Hydrogen Bond Theory, Oxford University Press, New York, 2009.
25. (a) A. Katrusiak and M. Szafrańsk, Phys. Rev. Lett., 1999, 82, 576–579; (b) M. Szafrański and A. Katrusiak, J. Phys. Chem. B, 2004, 108, 15709–15713.
26. J. D. Bernal and R. H. Fowler, J. Chem. Phys., 1933, 1, 515–548.
27. T. Akutagawa, S. Takeda, T. Hasegawa and T. Nakamura, J. Am. Chem. Soc., 2004, 126, 291–294.
28. S. Horiuchi, Y. Tokunaga, G. Giovannetti, S. Picozzi, H. Itoh, R. Shimano, R. Kumai and Y. Tokura, Nature, 2010, 463, 789–792.
29. S. Horiuchi, F. Kagawa, K. Hatahara, K. Kobayashi, R. Kumai, Y. Murakami and Y. Tokura, Nat. Commun., 2012, 3, 1308.
30. (a) Proton Conductors, solids, membranes and gels materials and devices, ed. P. Colomban, Cambridge University Press, Cambridge, 1992; (b) L. Glasser, Chem. Rev., 1975, 75, 21–65.
31. (a) P. Gilli, V. Bertolasi, V. Ferretti and G. Gilli, J. Am. Chem. Soc., 2002, 124, 13554–13567; (b) W. W. Cleland and M. M. Kreevoy, Science, 1994, 264, 1887–1890.
32. (a) T. Mochida, A. Izuoka, T. Sugawara, Y. Moritomo and Y. Tokura, J. Chem. Phys., 1994, 101, 7971–7974; (b) D. Merunka and B. Rakvin, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 132108.
33. (a) G. Saito and Y. Matsunaga, Bull. Chem. Soc. Jpn., 1971, 44, 3328–3335; (b) G. Saito and H. Inokuchi, Kagaku, Zokan, in Electroorganic Chemistry, ed. T. Osa, T. Shono, K. Honda, Kagaku Dojin, 1980, vol. 6, pp. 45–64; (c) Z. Malarski, M. Rospenk, L. Sobczyk and E. Grech, J. Phys. Chem., 1982, 86, 401–406; (d) I. Majerz, Z. Malarski and L. Sobczyk, Chem. Phys. Lett., 1997, 274, 361–364; (e) T. Akutagawa, T. Uchimaru, K. Sakai, T. Hasegawa and T. Nakamura, J. Phys. Chem. B, 2003, 107, 6248–6251.
34. A. Benjamin, Understanding Acid–Base, Taylor, 1998.
35. M. Tanaka, H. Matsui, J.-I. Mizoguchi and S. Kashino, Bull. Chem. Soc. Jpn., 1994, 67, 1572–1579.
36. (a) A. S. Verkman and A. K. Mitra, Am. J. Physiol. Renal. Physiol., 2000, 278, F13–F28; (b) M. Borgnia, S. Nielsen, A. Engel and P. Agre, Annu. Rev. Biochem., 2000, 68, 425–458.
37. B. Hille, Ionic Channels of Excitable Membranes, Sinauer Associates, Sunderland, 1992.
38. (a) R. M. Izatt, J. S. Bradshaw, S. A. Nielsen, J. D. Lamb, J. J. Christensen and D. Sen, Chem. Rev., 1985, 85, 271–339; (b) R. M. Izatt, K. Pawlak, J. D. Bradshaw and R. L. Bruening, Chem. Rev., 1991, 91, 1721–2085; (c) E. Weber, J. L. Toner, I. Goldberg, F. Vögtle, D. A. Laidler, J. F. Stoddart, R. A. Bartsch and C. L. Liotta, in Crown ethers and analogs, ed. S. Patai and Z. Rappoport, John Wiley & Sons, New York, 1989; (d) G. W. Gokel, in Crown Ethers & Cryptands, ed. J. F. Stoddart, RSC, Cambridge, 1994.
39. (a) A. W. Coleman, E. D. Silva, F. Nouar, M. Nierlich and A. Navaz, Chem. Commun., 2003, 826–827; (b) S. J. Iqbal, A. Mohamadi, P. Razavi, H. T. Dodd, M. C. Allen, S. Siddiqui, F. Fucassi and P. J. Cragg, J. Supramol. Chem., 2009, 21, 50–60.
40. (a) T. M. Fyles, Chem. Soc. Rev., 2007, 36, 335–347; (b) K. S. Åkerfeldt, J. D. Lear, Z. R. Wasserman, L. A. Chung and W. F. DeGrado, Acc. Chem. Res., 1993, 26, 191–197; (c) M. R. Ghadiri, J. R. Granja and L. K. Buehler, Nature, 1994, 369, 301–304; (d) G. W. Gokel and O. Murillo, Acc. Chem. Res., 1996, 29, 425–432; (e) J.-C. Meillon and N. Voyer, Angew. Chem., Int. Ed. Engl., 1997, 36, 967–969; (f) X. Zhou, G. Liu, K. Yamato, Y. Shen, R. Cheng, X. Wei, W. Bai, Y. Gao, H. Li, Y. Liu, F. Liu, D. M. Czajkowsky, J. Wang, M. J. Dabney, Z. Cai, J. Hu, F. V. Bright, L. He, X. C. Zeng, Z. Shao and B. Gong, Nat. Commun., 2012, 3, 949; (g) X. Hu, C. Yu, K. D. Okochi, Y. Jin, Z. Liu and W. Zhang, Chem. Commun., 2016, 52, 5848–5851.
41. (a) T. Nakamura, T. Akutagawa, K. Honda, A. E. Underhill, A. T. Coomber and R. H. Friend, Nature, 1998, 394, 159–160; (b) T. Akutagawa, T. Hasegawa, T. Nakamura, S. Takeda, K. Sugiura, Y. Sakata, T. Inabe and A. E. Underhill, Chem. – Eur. J., 2001, 7, 4902–4912; (c) T. Akutagawa, T. Hasegawa, T. Nakamura and T. Inabe, J. Am. Chem. Soc., 2002, 124, 8903–8911.
42. (a) N. Takamatsu, T. Akutagawa, T. Hasegawa, T. Nakamura, T. Inabe, W. Fujita and K. Awaga, Mol. Cryst. Liq. Cryst., 2000, 343, 163–168; (b) T. Akutagawa and T. Nakamura, Coord. Chem. Rev., 2000, 198, 297–311; (c) N. Takamatsu, T. Akutagawa, T. Hasegawa, T. Nakamura, T. Inabe, W. Fujita and K. Awaga, Inorg. Chem., 2000, 39, 870–871.
43. (a) P.-P. Shi, Y.-Y. Tang, P.-F. Li, W.-Q. Liao, Z.-X. Wang, Q. Ye and R.-G. Xiong, Chem. Soc. Rev., 2016, 45, 3811–3827; (b) D.-W. Fu, H.-L. Cai, Y. Liu, Q. Ye, W. Zhang, Y. Zhang, X.-Y. Chen, G. Giovannetti, M. Capone, J. Li and R.-G. Xiong, Science, 2013, 339, 425–428; (c) H.-Y. Ye, J.-Z. Ge, Y.-Y. Tang, P.-F. Li, Y. Zhang, Y.-M. You and R.-G. Xiong, J. Am. Chem. Soc., 2016, 138, 13175–13178; (d) Y.-M. You, W.-Q. Liao, D. Zhao, H.-Y. Ye, Y. Zhang, Q. Zhou, X. Niu, J. Wang, P.-F. Li, D.-W. Fu, Z. Wang, S. Gao, K. Yang, J.-M. Liu, J. Li, Y. Yan and R.-G. Xiong, Science, 2017, 357, 306–309.
44. (a) S. Chandrasekhar, Liq. Cryst., Cambridge Univ. Press, New York, 1992; (b) P. J. Collings and M. Hird, Introduction to Liquid Crystals, Chemistry and Physics, ed. G. W. Gray, J. W. Goodby and A. Fukuda, Taylor & Francis, London, 1997.
45. (a) W. I. F. David, R. M. Ibberson, T. J. S. Dennis, J. P. Hare and K. Prassid, Europhys. Lett., 1992, 18, 219–225; (b) Y. Jin, J. Cheng, M. Varma-Nair, G. Liang, Y. Fu, B. Wuaderlich, X.-D. Xiang, R. Mostovoy and A. K. Zettl, J. Phys. Chem., 1992, 96, 5151–5156.
46. (a) C. E. Nordman and D. L. Schmitkons, Acta Crystallogr., 1965, 18, 764–767; (b) P.-J. Wu, L. Hsu and D. A. Dows, J. Chem. Phys., 1971, 54, 2714–2721.
47. R. C. Yu, N. Tea, M. B. Salamon, D. Lorents and R. Malhotra, Phys. Rev. Lett., 1992, 68, 2050–2053.
48. (a) S. Nishihara, T. Akutagawa, T. Hasegawa and T. Nakamura, Chem. Commun., 2002, 408–409; (b) S. Nishihara, T. Akutagawa, T. Hasegawa, S. Fujiyama, T. Nakamura and T. Nakamura, J. Solid State Chem., 2002, 168, 661–667; (c) S. Nishihara, T. Akutagawa, D. Sato, S. Takeda, S. Noro and T. Nakamura, Chem. – Asian J., 2007, 2, 1083–1090.
49. K. C. Kao, Dielectric Phenomena in Solids, Elsevier, Amsterdam, 2004.
50. T. Akutagawa, H. Koshinaka, D. Sato, S. Takeda, S.-I. Noro, H. Takahasi, R. Kumai, Y. Tokura and T. Nakamura, Nat. Mater., 2009, 8, 342–347.
51. J. Ichikawa, N. Hoshino, T. Takeda and T. Akutagawa, J. Am. Chem. Soc., 2015, 137, 13155–13160.
52. V. R. Pedireddi, D. S. Reddy, B. S. Goud, D. C. Craig, A. D. Rae and G. R. Desiraju, J. Chem. Soc., Perkin Trans. 2, 1994, 2353–2360.
53. J. G. Nicholls, A. R. Martin, D. A. Brown, M. E. Diamond, D. A. Weisblat and P. A. Fuchs, From Neuron to Brain, Sinauer Association Inc., Sunderland, USA, 2000.
54. S. Erbas-Cakmak, D. A. Leigh, C. T. McTernan and A. L. Nussbaumer, Chem. Rev., 2015, 115, 10081–10206.
55. A. V. Akimov, D. Mandal, V. Y. Chernyak and N. A. Sinitsyn, J. Chem. Phys., 2013, 138, 024109.
56. A. B. Kolomeisky and M. E. Fisher, Annu. Rev. Phys. Chem., 2007, 58, 675–695.

---