Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Laser inscription of pseudorandom structures for microphotonic diffuser applications†
Tawfiq
Alqurashi
 *ab,
Abdulla
Alhosani
bc,
Mahmoud
Dauleh
b,
Ali K.
Yetisen
*ab,
Abdulla
Alhosani
bc,
Mahmoud
Dauleh
b,
Ali K.
Yetisen
 d and
Haider
Butt
d and
Haider
Butt
 *b
*b
aDepartment of Mechanical Engineering, School of Engineering, Shaqra University, P.O. Box 90 Zip Code 11921, Dawadmi, Saudi Arabia
bSchool of Engineering, University of Birmingham, Birmingham, B15 2TT, UK. E-mail: talqurashi@su.edu.sa; h.butt@bham.ac.uk
cDepartment of Mechanical Engineering, Imperial College of Science, Technology and Medicine, Prince Consort Road, London, SW7 2AZ, UK
dHarvard-MIT Division of Health Sciences and Technology, Harvard University and Massachusetts Institute of Technology, Cambridge, MA 02139, USA
First published on 14th March 2018
Abstract
Optical diffusers provide a solution for a variety of applications requiring a Gaussian intensity distribution including imaging systems, biomedical optics, and aerospace. Advances in laser ablation processes have allowed the rapid production of efficient optical diffusers. Here, we demonstrate a novel technique to fabricate high-quality glass optical diffusers with cost-efficiency using a continuous CO2 laser. Surface relief pseudorandom microstructures were patterned on both sides of the glass substrates. A numerical simulation of the temperature distribution showed that the CO2 laser drills a 137 μm hole in the glass for every 2 ms of processing time. FFT simulation was utilized to design predictable optical diffusers. The pseudorandom microstructures were characterized by optical microscopy, Raman spectroscopy, and angle-resolved spectroscopy to assess their chemical properties, optical scattering, transmittance, and polarization response. Increasing laser exposure and the number of diffusing surfaces enhanced the diffusion and homogenized the incident light. The recorded speckle pattern showed high contrast with sharp bright spot free diffusion in the far field view range (250 mm). A model of glass surface peeling was also developed to prevent its occurrence during the fabrication process. The demonstrated method provides an economical approach in fabricating optical glass diffusers in a controlled and predictable manner. The produced optical diffusers have application in fibre optics, LED systems, and spotlights.
Introduction
Optical diffusers are wavefront processors used to alter the intensity distribution of an incident light beam into a specified pattern.1,2 They are widely used in imaging systems, LED displays, and barcode scanners to provide uniform light exposure and eliminate high-intensity spots.3–7 Depending on the incorporated light scattering method, optical diffusers are classified as the volumetric or surface relief types.8 Volumetric diffusers scatter the light via transparent microscopic beads and/or fillers trapped inside the surface that cause the light to diverge as it is transmitted through the material.9,10 However, this article focuses on the surface-relief type, which utilizes unique nano- and microstructures on the diffuser surface to scatter light. The fabrication of these nano- and microscale surface relief structures (e.g. pyramids, microlens arrays and textured rough surfaces) is a rapidly growing area of interest.11–13 Surface relief structures are the most common diffusers due to simplicity and reliable processing time during fabrication compared to volumetric diffusers.Over the past few decades, various fabrication methods including holographic recording,14 replica molding,12 ink printing,15 and surface texturing8,16 were utilized to produce microstructured diffuser surfaces. Advanced continuous wave (CW) CO2 laser based systems rival the traditional lasers (e.g. Nd:YAG and femtosecond lasers) in the fabrication of optical diffusers.17 Moreover, due to their high efficiency, high power,18 and low capital cost,19 CO2 laser based systems are more economical in the fabrication of optical diffusers via laser inscription processes. In particular, CW CO2 lasers are widely used in micromachining soda-lime silicate glasses due to the high radiation absorption of silicate glasses at a wavelength of 10.6 μm.20 Additionally, the low thermal conductivity, heat treatability and relatively low cost make soda-lime glasses the optimal material for CO2 laser processing.21 Machining glass substrates using laser inscription processes can alter their physical properties,22 which may result in modified surface wettability, conductivity, and optical properties.23–25
Surface relief diffusers diverge the light emulating negative lens, thus their performance is usually characterized by the intensity of the light transmitted and its diffusion angle (α).26 The diffusion angle (α) is defined as the maximum exit angle of the light when it is passed through a diffusing material, and it is determined by the Full Width at Half Maximum (FWHM) of the light intensity diffusion profile.8 The optical performance, light homogenization level and efficiency of an engineered optical diffuser can vary depending on its diffusion angle.27 Typical diffusion angles of glass-based optical diffusers range from 0.2° to 100° depending on the required application.28 Low diffusion angles (5°–25°) are particularly desirable in filament lamps and fluorescent lamps,22 where homogenizing the light without excessively diverging the beam is necessary to remove the hot spots and to provide an even light distribution. On the other hand, optical diffusers with wider angles are already used to disperse light evenly across the screens of laptops, smartphones, and instrument panels.29,30
This research study reports a novel technique for fabricating surface relief optical glass diffusers using a CW CO2 laser. The fabrication method differs from the established conventional techniques as direct laser inscription of glass substrates was performed without coating the glass surface in the present work.15,31,32 Additionally, other polished optical diffusers have shown low FWHM scattering (20°). The presented technique provides a fast and economically viable approach for fabricating glass optical diffusers compare to femtosecond laser.33,54 A numerical model was developed to simulate the laser ablation process on the soda-lime glass substrates. This study examines the effect of implementing different surface relief microstructures and increasing the diffusing surfaces on the optical performance. The fabricated surface was characterized using optical microscopy and Raman spectroscopy to examine its structural morphology and chemical properties. The optical scattering and transmission efficiency of the produced diffusers were assessed using an angle-resolved intensity measurement setup and spectroscopic analysis. The glass surface peeling phenomenon was also examined and a prediction model was constructed.
Results and discussion
FEM simulations of laser ablation on glass substrates
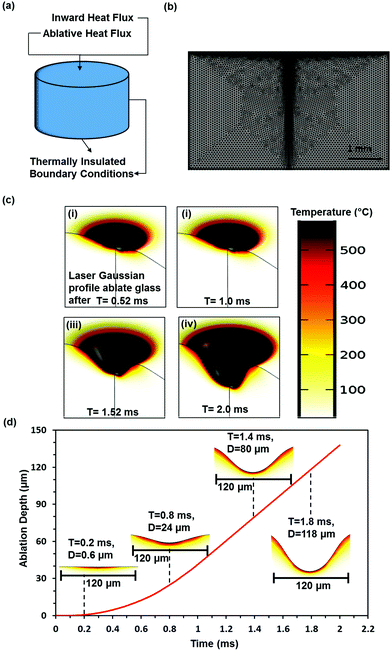
To investigate the surface morphologies produced on the soda-lime glass substrates due to CO2 laser ablation processing, a numerical model was developed. Multiple studies have been conducted to simulate laser ablation processes; however, most of them focused mainly on simulating pulsed lasers. A 3D model has been developed to predict the temperature distribution and material removal during nanosecond laser ablation of various materials.34 Therefore, an analogous approach was adopted in this study for a continuous CO2 laser. The Finite Element Analysis (FEA) method was utilized to simulate the model. This simulation demonstrates the effect of the laser intensity profile on the temperature distribution and the shape of the irradiated region. Given the increased complexity in modelling real life laser ablation problems, few assumptions were made to produce a feasible simulation without affecting the primary outcome of the study. These assumptions are as follows: (i) the maximum temperature is developed on the surface of the model and there is no internal heating that could lead to an internal gas-filled void within the solid material. This limits the sublimation process to occur on the exposed layer of the material only. (ii) Once the material transitions into the gas phase, its thermal significance vanishes. This excludes the necessity to model the thermal properties of the vaporized material around the heated surface.Theoretical model
Modelling the ablation process involved creating a model that governed temperature variations with time. Therefore, the conduction transient energy transport equation was used as the primary in domain heat transfer mode: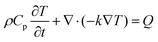 | (1) |
| Q = I × α × (1 − R) | (2) |
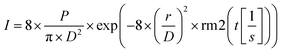 | (3) |
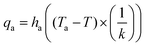 | (4) |
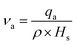 | (5) |
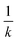 is a growing specific heat capacity for T > Ta, to ensure that the material absorbs more energy at high temperatures to sublimate.
is a growing specific heat capacity for T > Ta, to ensure that the material absorbs more energy at high temperatures to sublimate.
FEM modelling
To start the simulation process, a geometry with a radius of 3 mm and a height of 4 mm was created to model the glass substrate in finite element method simulations. Eqn (1)–(5) were applied to the created geometry in the form of boundary conditions to model the laser ablation process. The dimensions and boundary conditions are described in Fig. 1a and b. The inward and ablative heat flux boundary conditions applied to the top surface represent the heat transfer from the laser source, while the thermal insulation boundary condition was employed in the bottom and lateral surfaces to limit the heat loss from the material body.The laser properties, material properties and ambient conditions were defined, as shown in ESI Table 1.† A uniform triangular mesh with a minimum element size of 1.2 μm was generated for the domain. To increase the accuracy of the model, an additional 0.3 μm mesh was created using the sizing function and applied to the top surface and along the geometry center line to capture the deformation due to material removal efficiently. The meshed geometry is shown in Fig. 1b. The laser processing time was set to 2 ms and the model was solved.
At the initial stage of the laser ablation process, microscopic particles begin to fracture from the glass surface allowing the post ablation effects to take place on the surface. During the ablation process of glass, a roll of solidified melt called recast forms at the edges of the ablated structure due to the material being melted and ejected out of the surface.38 Additionally, a debris layer is deposited around the structure due to the precipitation of the vaporized material. However, the simulation assumes the direct sublimation process of the material. Therefore, the melting and precipitation effects are not accounted for in the simulation.
Fig. 1c shows the temperature distribution and the profile of the propagating concavity in the ablated region with time. The exposed glass layer experiences almost a constant temperature (500 °C) at the point of the laser beam focus, while the surface temperature cools down as the depth of the concavity increases. Fig. 1(civ) shows the formed concavity profile when the material was ablated for 2 ms using a laser with a Gaussian intensity distribution. The Gaussian distribution intensity is concentrated at the center of the beam, thus resulting in a non-uniform hole shape with the maximum depth at the center. Hence, CO2 lasers are less efficient in drilling holes of uniform sizes. Fig. 1d shows the ablation depth against the laser exposure time. Increasing the laser processing time increased the material removal with a linear correlation. A concavity with a 137 μm depth formed on the glass surface after 0.2 ms processing time. Hence, laser ablation was a time dependent process; thus, by controlling the laser machining time, the depth and shape of the hole could be controlled.
Optical diffuser fabrication and surface characterization
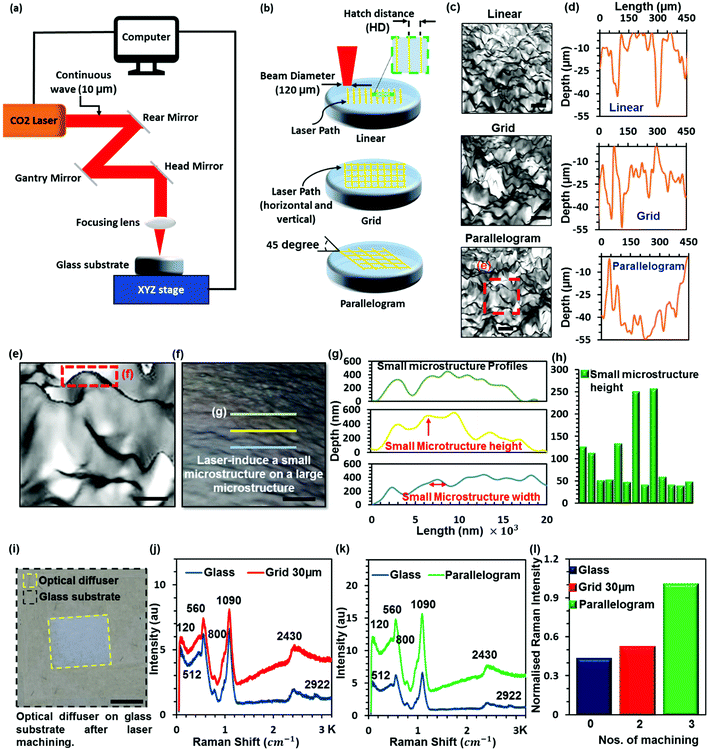
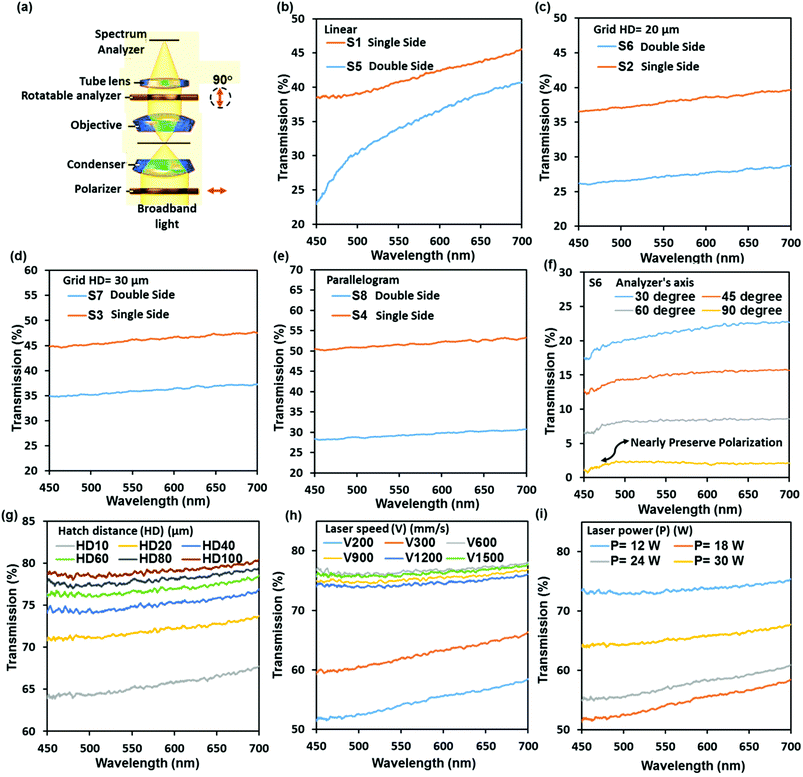
Surface relief diffusers utilize a complex microstructure to perform their optical function. According to Huygens’ principle,40 optical diffusers modify wavefronts by segmenting and redirecting the segments through the use of interference and phase control, which is mainly controlled by the microstructure on the surface. Hence, by controlling the microstructure, the angular distribution of the incident light in the far field can be controlled. Common surface relief diffusers have profiles with two or more surface levels. This can be achieved by overlapping laser exposure on the surface of the diffuser. Fig. 2a shows a schematic of the CO2 laser setup. In this experiment, three different surface patterns were employed during the fabrication stage to determine the effect of varying the microstructure on the optical characteristics. The linear, gird and prismatic patterns are shown in Fig. 2b. The grid structure incorporates overlapping laser exposure, where the surface was initially machined in the vertical direction and then left to cool down before machining it in the horizontal direction. The parallelogram pattern is similar to the grid pattern; however, the angle between the machining lines was reduced from 90° to 45°. Overlapping the laser inscription produces small pseudorandom, non-periodic microstructures superimposed on a large pseudorandom microstructure (Fig. 2c). Fig. 2d shows the profile of large microstructures having a microstructure with a width of 35 μm and a depth of 20 μm. The large microstructure was superimposed with a small microstructure (Fig. 2f) within the range of 1.5 to 2.5 μm in width and 50 to 200 nm in height (Fig. 2g and h). These large area (5 × 5 mm) non-periodic microstructures (Fig. 2i) cause the diffusion of light by randomizing the reflection of collimated incident laser beams.30Prior to implementing the surface micropatterns onto the float glass substrates, optimal laser operating parameters were specified. The specification of the laser parameters was determined for achieving the optimum optical performance: a beam power of 24 W, a scanning speed of 300 mm s−1 and a hatch distance of 10 μm (ESI, Fig. S1†). However, in the case of the surface relief profiles that require overlapping laser inscriptions, the hatch distance was doubled to prevent surface peeling of glass and heterogeneous surface morphology. Throughout the fabrication stage, the peeling of the glass surface was a limiting factor in employing the desired laser parameters and it was eliminated by using an experimental prediction model (ESI, Fig. S2†).
Initially, the optical diffusers were fabricated by machining the linear, grid and parallelogram microstructures on one side of the float glass substrate. Surface relief profiles were also produced on both sides of the diffuser slide samples. Incorporating two or more diffusing surfaces can alter the diffusion characteristics of the microphotonic devices. As the incident light hits the first diffuse surface, the collimated light beams are scattered off the surface at different angles. This leads to beam scattering with small angles to force and propagate light through the material. Thus, employing a second diffuser surface on the other side of the substrate can further spread out the light beam propagating through the material, hence altering the homogeneity and the diffusion efficiency of the glass substrates.
Here, CW CO2 laser inscription was utilized to produce a variety of optical diffusers by using different laser parameters (Table 1). After each process, the reflecting mirrors of the laser system were cleaned to maintain a high accuracy of the laser inscription. The microstructures of the produced samples were imaged using optical microscopy (ESI, Fig. S3†). A maximum of 2 and 4 min processing time was needed to produce the one-sided and double diffusers, respectively. Alternative fabrication methods (e.g. rolling) have higher production rates for fabricating polyester and polycarbonate diffuser sheets; however, they cannot be used to fabricate glass diffusers.
| Sample | Pattern | Diffuser surface side | HD (μm) |
|---|---|---|---|
| S1 | Linear | Single | 10 |
| S2 | Grid | Single | 20 |
| S3 | Grid | Single | 30 |
| S4 | Parallelogram | Single | 20 |
| S5 | Linear | Double | 10 |
| S6 | Grid | Double | 20 |
| S7 | Grid | Double | 30 |
| S8 | Parallelogram | Double | 20 |
Furthermore, Raman spectra of a laser modified soda lime glass slide (optical diffuser) with an unmodified soda lime glass slide were recorded at a 50× objective with a 532 nm laser. Soda lime glass is a non-crystalline form of sodium oxide (soda) and calcium oxide (lime). The intense bands observed for modified and nonmodified soda lime glass can be assigned to the bending of silicone bridging oxygen at 480 cm, the symmetric stretching of bridging oxygen at 630–740 cm, the symmetric stretching with different numbers of non-bridging oxygen at 850–1050 cm, and the symmetric stretching of bridging oxygen at 1100 cm. The weak band at 2350 cm has been assigned to the Si–OH groups involved in intratetrahedral hydrogen bonding across an edge of the SiO4 tetrahedron.41–43
The Raman spectra obtained for soda lime glass (the unmodified surface), grid 30 μm and a parallelogram optical diffuser (the modified surface) have six bands at 120, 512, 560, 800, 1090 and 2430 cm−1 except that the unmodified glass shows one more band at 2922 cm−1 (Fig. 2j and k). The Raman spectra of the modified and unmodified glass slides recorded have prominent and intense bands around 120, 560, 1090 and 2430 cm−1 with weak shoulder bands at 512 cm−1. Additionally, two weak intense bands appear at 512 and 800 cm−1 and a weak hump around 2922 cm−1. The peak at 2922 cm−1 disappears on modified glasses. However, the intensity of bands at 512 and 800 cm−1 is higher compared with the Raman spectrum of unmodified soda lime glass and increased with the repeating number of glass machining. This is due to the fundamental vibration of soda lime glass after laser processing. It has been reported that the Raman intensity increased with either increasing the heat treatment temperature or increasing the compression pressure in glass.44,45
Optical characterization of microphotonic diffusers
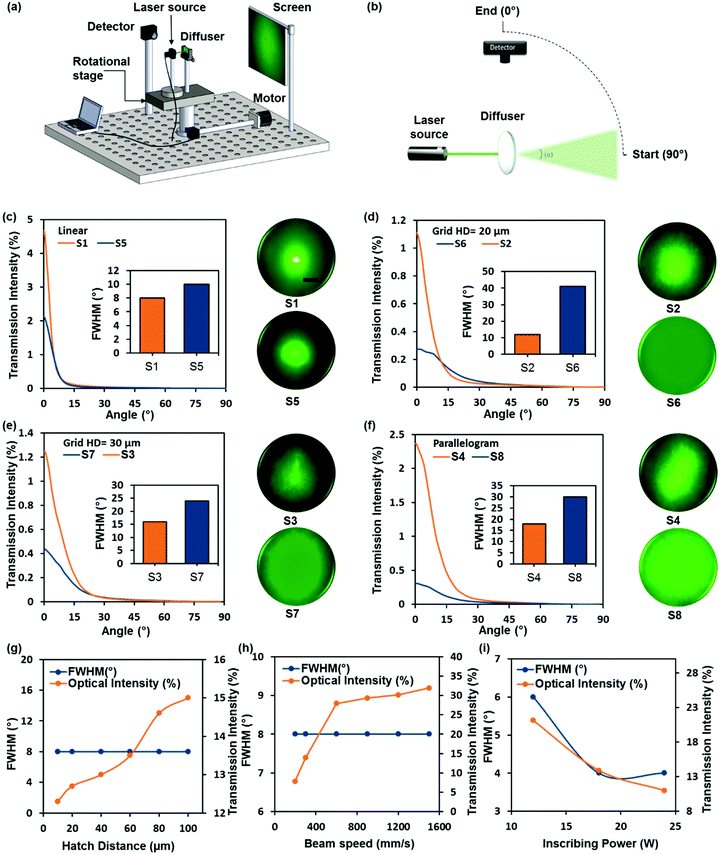
The optical performance of the glass-based optical diffusers was determined using an angular light distribution measurement setup including a digital camera and a spectrophotometer. The angle-resolved measurement setup was used to determine the light diffusion intensity profiles of the glass diffusers. Fig. 3a and b show the setup consisting of a laser pointer, a microphotonic diffuser and an optical detector to measure the scattered light intensity at various angles. The laser pointer and the diffuser were mounted on a 360° continuous rotation stage with a stepper motor actuator controlled by a computer. This setup allows setting operating parameters. The confined rotation of the light source and the sample ensures that the incident light remains normal to the diffuser surface. The stage was rotated from +90° to the incident normal (0°), and the photometer recorded the intensity of the diffused light at 2° rotation increments to characterize the diffuser beam shape including its diffusion angle, the FWHM of the diffusion angle, and the intensity profile. This setup was calibrated after every rotation to ensure the high reliability of the measurements.Fig. 3c–f show the light intensity profiles and the scattering patterns of the fabricated diffusers when illuminated with a green laser pointer (λ = 532 nm). The diffused light profiles exhibited a Gaussian illumination distribution, which indicated that the light diffusion was caused by the variations in surface topography features.31 The diffusion characteristics were compared between one-sided and double-sided diffusers with the same patterns. As expected, two-sided diffusers displayed greater diffusion angles, and their capabilities to diffuse light were almost twice those of the one-sided diffusers. The FWHM of diffusion angles ranged from 8° to 41°, where the smallest angles were recorded for the linear surface pattern while the grid and parallelogram patterns displayed higher diffusion angles. The highest diffusion angles were obtained to be 41°, 30° and 24° with peak transmission intensities of ∼29%, ∼39% and ∼42% for samples S6, S8 and S7, respectively. The variation in the thickness of the glass layers causes the energy of the particles to be dependent on their in-plane location in the layer, thus resulting in a roughness-dependent light scattering profile which shows the importance of the design of the structure embedded on the surface.46
A collimated green laser beam was used to illuminate the diffuser surfaces, and their scattering patterns in the far field were captured off a projection screen using a digital camera. Fig. 3c shows that the linear one-sided diffuser (S1) displayed a higher intensity density at the 0th order compared to the double-sided diffuser (S5), which showed slightly wider diffusion at the center. However, the intensity at the 0th order for the linear surface relief diffuser was high. On the other hand, the one-sided diffusers S2, S3 and S4 fabricated using the overlapping grid and parallelogram micropatterns displayed relatively high diffusion angles but with non-homogenous illumination, resulting in different areas receiving more/less light intensity. Furthermore, the double-sided grid and parallelogram microstructures (S6, S7 and S8) showed the most efficient diffraction patterns with an even intensity distribution and high diffusion homogeneity across the illuminated surface. Light homogenization and high diffusion angles are critical factors in determining the efficiency of optical diffusers. Therefore, the proposed method of producing overlapping grid and parallelogram patterns on two sides of the glass substrates has the potential in fabricating high-quality optical diffusers.
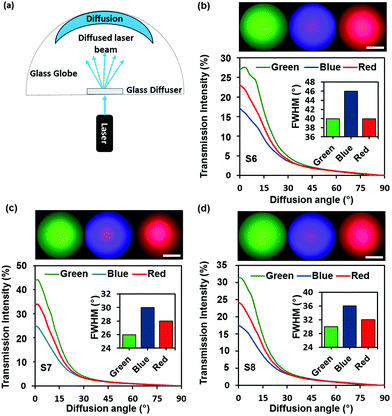
To visualize the effect of varying the wavelength on the distribution of the diffused light, a setup (Fig. 4a) was used to capture off the scattering image projected on the screen. The diffusion profile depends strongly on the wavelength or frequency of the transmitted light. Therefore, samples S6, S7 and S8 that displayed the highest diffusion angles were analysed against varying laser sources (λ1 = 450 nm, λ2 = 533 nm, λ3 = 633 nm). The diffusion plots of the samples with their respective diffusion patterns are shown in Fig. 4b–d. The highest FWHM of the diffusion angle was 46° in response to the blue laser for the grid micropattern S6, where the diffuser displayed a lower intensity (∼16%) at the 0th order (Fig. 4b). Furthermore, the correlation between the diffusion angle and the transmitted light wavelengths was ambiguous as the optical diffusers showed higher diffusion angles at the shortest and longest wavelengths (λ1 = 450 nm & λ3 = 633 nm), while the moderate light wavelength (λ2 = 532 nm) displayed the lowest diffusion angles.
The double sided grid and parallelogram micropatterns (S6, S7 and S8) were illuminated with three different collimated laser sources and the observed light scattering patterns were captured using a white globe. A semi-transparent spherical globe was utilized due to its capability to provide the visual representation of wide scattering patterns. Fig. 4b–d show the different diffusion patterns produced. Almost all the diffusers reacted to varying wavelengths in a similar manner; thus, further comparisons were conducted on the patterns produced by the blue, green, and red laser beams. The optical diffusion field of view increased from ∼172° for the green laser to ∼177° for the blue and red lasers.
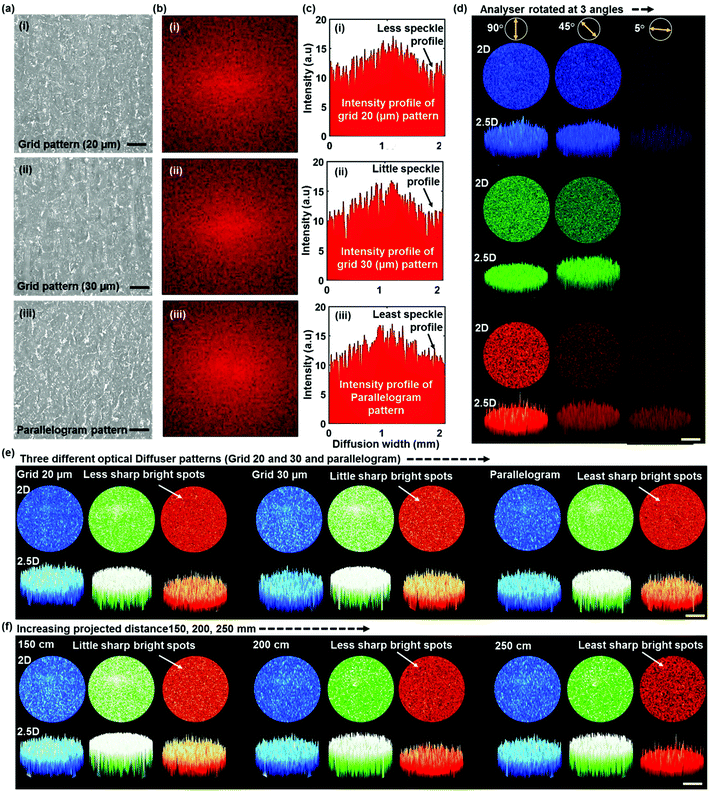
A Fast Fourier Transform (FFT) simulation47,48 and a 2D/2.5D speckle imaging experiment were performed to assess the relationship between the pseudorandom microstructures and light scattering from optical diffusers. The difference between the simulation and the experimental results determines the homogeneity of light diffusion. The FFT simulation was employed to predict the optical characteristics of the diffusers (Fig. 5b and c). These simulations were analyzed based on the optical images obtained from normal incidence in transmission mode (Fig. 5a). The simulated image produced speckles with a wide range of bright region in the centre of the image and the bright region reduced with the increase of the dark region towards the edge. At the zero order, the light scattering area increased from the grid to parallelogram pattern diffuser. The intensity profile revealed that the intensity profile of the parallelogram pattern diffuser was smooth compared to the grid patterned diffuser.
2D/2.5D speckle imaging was conducted experimentally to analyze the speckle/diffusion pattern. In a polarization experiment, the sample was mounted on a holder, and the diffuser was placed between the linear polarizer and analyzer to make the laser linearly polarized and to adjust the analyzer at 5°, 45° and 90° from the normal. Collimated laser sources (450, 533 and 633 nm) were located on one side and a high-resolution imaging camera with a complementary metal–oxide–semiconductor (CMOS) sensor was placed on the opposite side of the optical diffuser. This allowed photons to propagate through the diffuser and capture a 2D high-resolution image via the CMOS sensor. The 2D recorded image was used to reconstruct a 2.5D image (intensity profile) using optical image processing.
The diffuser (HD = 30 μm) generated speckle patterns preserved the linear polarization of the laser beam incident normally to the plane at the horizontal polarizer (0°), but the image was recorded at an angle of 5° with respect to the surface plane due to low light intensity (Fig. 5d). Thus, the diffusion pattern can be controlled by modifying the polarization orientation. Three optical diffusers with different fabrication patterns produced a speckle intensity distribution in the far field upon illumination with monochromatic light (Fig. 5e). The speckled patterns consisted of highly intense spots and bright and dark regions over an area with 5 mm diameter. In general, the sharp bright spots increased slightly from the parallelogram diffuser to the grid (HD = 30 μm) diffuser. Additionally, the speckle pattern was studied at different projection lengths. Over 90% of highly intense spots were reduced with increasing projection length from 15 to 25 cm. This provides sufficiently high contrast with the sharp bright spot free condition in the long far field view range. ESI, Fig. S4† provides additional speckle pattern images of other diffusers. This optical diffuser can be utilized as part of an imaging device, in which scattered light can be used for image reconstruction.49,50
Broadband light transmittance was utilized to assess the performance of the fabricated optical diffusers. A typical soda lime glass substrate having a thickness of 2 mm has a transmittance of ∼90% across the visible spectrum. The spectral transmittance measurement setup consisted of a broadband light source and a spectrometer (2 nm resolution) connected to an optical microscope via an optic fiber. For transmitted light polarization measurement, the experimental setup had a linear polarizer and analyser, which were underneath and above the optical diffuser, respectively. This allowed to have linearly polarized light before it passed through the diffuser and to control and modify the polarization direction, and to measure its effect on transmittance measurement. Fig. 6a shows a schematic of the spectral transmittance measurement setup integrated with two polarizers.
Fig. 6b–i show the transmittance of the fabricated diffusers as a function of the incident wavelength (450–700 nm). The results indicated that one-sided diffusers were more efficient in transmitting visible light than double sided diffusers. The parallelogram diffuser (S4) showed the highest transmission (∼50%), thus the parallelogram structure was considered to be the most efficient one-sided structure as it also revealed the highest diffusion angle (18°) for one-sided diffusers (Fig. 3d). The spectral transmittance of diffusers S6, S7 and S8 that showed the highest diffusion angles was ∼25%, ∼35% and ∼28%, respectively. Hence, it is observed from the grid samples S6 (HD = 20 μm) and S7 (HD = 30 μm) that increasing the hatch distance increases the transmittance of the diffuser, but results in a lower diffusion angle. It can be deduced that the double-sided diffuser fabrication technique negatively influenced the transmittance of the optical diffuser. This is attributed to the increase in the number of diffusing surfaces, thus having additional microsurface features that can further scatter the incident light. However, the use of an additional anti-reflective coating on the surface of the diffusers can improve the transmittance of the diffusers by reducing the reflection from the diffusion surfaces.
Glass surface peeling
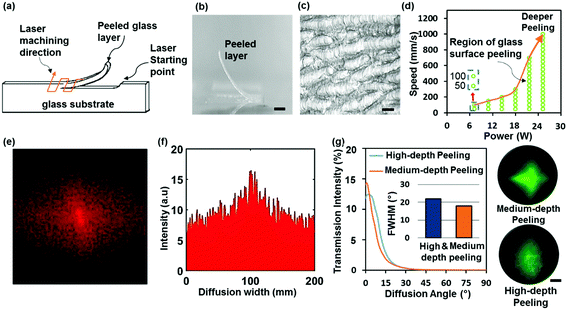
Surface peeling is defined as the continuous removal of a thin layer from the surface of an ablated material.51,52 The removed layer is usually of a constant thickness. Applications of glass surface peeling include improving the surface finish of laser cutting glass products and forming microchannels on glass substrates for optofluidic devices.53 Laser cutting of glass substrates induces the formation of defects on the cutting edges which acts as starting point for cracks to propagate through the material.52 Thus, peeling off the cutting-edge layer that contains these defects can strengthen the material and create a defect free surface.36 Glass surface peeling is a function of the energy deposition rate on the surface, which in turn depends on the input laser power and scanning speed.51 When the ratio of the two parameters results in an energy deposition rate in the range of 3.0–6.0 J (cm2 s)−1, the temperature inside the material exceeds the strain point and reaches the softening point of the glass, where a thin layer starts to separate from the surface. Fig. 7a shows a glass substrate experiencing surface peeling. The formed microstructure on the surface of the glass due to surface peeling indicates that multiple microchannels with varying lengths are engraved on the substrate (Fig. 7b). In Fig. 7c, a strip was peeled off the diffuser surface, showing the material removal from the surface of the diffuser in the peeled region.Throughout the experiments, glass surface peeling was a key factor in determining the optimum laser operating parameters. During the fabrication stage, the samples that experienced surface peeling were discarded from the experiment and considered to be in-viable optical diffusers. Therefore, it was essential to develop a glass surface peeling prediction model based on experimental data. Fig. 7a shows a schematic of the surface peeling process with the adopted texturing pattern (a linear pattern). A hatching distance of 10 μm was implemented within the texturing pattern to authenticate the prediction model with the parameters employed in the fabrication stage.
Fig. 7d shows the experimental prediction model of glass surface peeling for a CW CO2 laser. The graph indicates that the ratio of the laser power and speed must fall outside the shaded region to avoid glass surface peeling. At low laser powers (12–30 W), it is necessary to maintain a linear relationship between the two parameters to prevent the induction of glass layer peeling, while at higher laser powers (+30 W) the speed must be doubled. This is due to the high material removal rate from the surface at high laser powers. Fig. 7g shows the diffusion plots of two glass slides that exhibited surface peeling with their respective scattering patterns. The high-depth peeling sample (P = 42 W, V = 100 mm s−1, and HD = 10 μm) experienced material removal, which resulted in a thicker layer being peeled from the surface. The peeled layer was detached from the glass surface and its optical diffusion properties were measured. A diffusion angle of 22° was obtained for the high-depth peeling sample. The sample produced a heterogeneous diffusion pattern with reduced intensity at the 0th order when the surface was illuminated with a green laser beam. On the other hand, the medium-depth peeling sample (P = 12 W, V = 50 mm s−1, HD = 10 μm) that exhibited thin layer removal from the surface showed a lower diffusion angle (17°) with a defined transmission peak intensity of ∼1.4%. The sample also displayed a random cross-shaped diffusion pattern. The obtained diffusion characteristics of the peeled samples indicate that they are inviable to be used as efficient optical diffusers. Moreover, the most popular method is the use of a holographic diffuser, which relies on the surface structure of various shapes to spread out light. However, this method falls short due to the finer structures, which are easier to get damaged chemically or mechanically.
Conclusion
The work demonstrated the viability of producing glass based optical diffusers using direct CO2 laser writing. The proposed approach of fabricating overlapping surface relief structures on both sides of the glass substrates was successful and its direct influence on enhancing the optical performance of glass diffusers was measured. The characteristics of diffusers fabricated using this method can be altered by changing the microstructures including linear, grid and parallelogram patterns. This novel technique provides a fast and economically viable approach in the massive fabrication of optical diffusers. The diffusion measurements showed that structures with overlapping laser exposure were efficient diffusers. Increasing the number of diffuser surfaces resulted in wider scattering patterns and increased homogeneity. The highest diffusion angles were recorded for the two-sided grid diffuser with HD = 20 μm, which are 46°, 42° and 41° in response to wavelengths of 450, 633 and 532 nm, respectively. The broadband light transmission of the fabricated samples decreased when the structures were patterned on both sides. The parallelogram structure displayed the highest (∼50%) broadband light transmission across the visible range. A prediction model of glass surface peeling induced by the CW CO2 laser was constructed to avoid the formation of thin rolled glass layers on the surface of the produced diffusers. The diffusion characteristics of the peeled samples were determined and their negative impact on the diffuser performance was determined. The laser ablation process on the glass substrates was simulated to create a model, which displayed the temperature variations on the ablated region together with the material removal rate. The Gaussian profile of the laser intensity distribution resulted in non-uniform concavity formation on the surface of the material with a maximum depth of 0.5 mm in the center, after 2 ms ablation time. The conducted experiments demonstrated a rapid and accurate fabrication method for high-quality glass diffusers that can serve multiple optical functions. Future studies on enhancing the optical performance of the fabricated diffusers can involve additive surface coatings or implementation of this approach in materials with higher light transmittance capabilities.Experimental section
A CW CO2 laser
The diffusers were fabricated by machining a surface relief pseudorandom microstructure on float glass slides (thickness ∼1.1 mm). The patterns were implemented using a desktop laser setup (LS3040, HPC Laser Ltd, UK). The desktop setup utilizes a CW CO2 laser as the heating source with a maximum power of 60 W and a wavelength (λ) of 10.6 μm. The laser features an adjustable optic head and platform configuration, where the substrates are mounted on a z-axial translation stage and the laser head moves in the x–y horizontal axes. The laser operates at a maximum engraving speed of 1500 mm s−1 within a 420 × 300 mm work area. The laser beam focus on the glass surface is provided by a ZnSe lens (focal length ∼28.1 mm and the minimum spot diameter ∼180 μm). Finally, the desired machining patterns can be imported from computer-aided modelling software.A high-resolution imaging camera
The speckle pattern was recorded using an AXIOCAM 105 color with a basic resolution of 5 megapixels and integrated with a complementary metal–oxide–semiconductor (CMOS) sensor from Carl ZEISS company. This camera was placed on a holder and connected to an optical microscope and the microscope was connected to a computer to provide the speckled pattern image on the screen.Conflicts of interest
We declare no competing financial interests.Acknowledgements
H. B. thanks the Leverhulme Trust for the research funding. T. A. thanks Saudi Arabian cultural Bureau in London for the research funding.References
- M. Sparvoli and R. D. Mansano, Glass Difractive Optical Elements (DOEs) with complex modulation DLC thin film coated, Mater. Res., 2008, 11, 341–345 CrossRef CAS.
- M. Nixon, et al., Real-time wavefront shaping through scattering media by all-optical feedback, Nat. Photonics, 2013, 7(11), 919–924 CrossRef CAS.
- J. Hu, Y. Zhou and X. Sheng, Optical diffusers with enhanced properties based on novel polysiloxane@CeO2@PMMA fillers, J. Mater. Chem. C, 2015, 3(10), 2223–2230 RSC.
- T.-C. Huang, et al., Fast fabrication of integrated surface-relief and particle-diffusing plastic diffuser by use of a hybrid extrusion roller embossing process, Opt. Express, 2008, 16(1), 440–447 CrossRef PubMed.
- A. K. Singh, et al., Exploiting scattering media for exploring 3D objects, Light: Sci. Appl., 2017, 6, e16219 CrossRef CAS.
- G. Donati, Optical imaging: Light scattering on tape, Nat. Photonics, 2017, 11(3), 141–141 CrossRef CAS.
- E. R. Méndez, et al., Photofabrication of random achromatic optical diffusers for uniform illumination, Appl. Opt., 2001, 40(7), 1098–1108 CrossRef.
- T. Alqurashi, et al., Femtosecond laser directed fabrication of optical diffusers, RSC Adv., 2017, 7(29), 18019–18023 RSC.
- H. Butt, et al., Devitrite-Based Optical Diffusers, ACS Nano, 2014, 8(3), 2929–2935 CrossRef CAS PubMed.
- H. Butt, et al., Electrically Tunable Scattering from Devitrite–Liquid Crystal Hybrid Devices, Adv. Opt. Mater., 2017, 5(1), 1600414 CrossRef.
- R. Ahmed, A. K. Yetisen and H. Butt, High Numerical Aperture Hexagonal Stacked Ring-Based Bidirectional Flexible Polymer Microlens Array, ACS Nano, 2017, 11(3), 3155–3165 CrossRef CAS PubMed.
- C. Yi Wu, T. H. Chiang and C. C. Hsu, Fabrication of microlens array diffuser films with controllable haze distribution by combination of breath figures and replica molding methods, Opt. Express, 2008, 16(24), 19978–19986 CrossRef.
- S.-I. Chang, et al., Microlens array diffuser for a light-emitting diode backlight system, Opt. Lett., 2006, 31(20), 3016–3018 CrossRef PubMed.
- D. Sakai, et al., Direct Fabrication of Surface Relief Holographic Diffusers in Azobenzene Polymer Films, Opt. Rev., 2005, 12(5), 383–386 CrossRef CAS.
- R. Ahmed, et al., Printable ink lenses, diffusers, and 2D gratings, Nanoscale, 2017, 9(1), 266–276 RSC.
- T. Alqurashi, et al., Nanosecond pulsed laser texturing of optical diffusers, AIP Adv., 2017, 7(2), 025313 CrossRef.
- L. Yi, A. Pukhov and B. Shen, Direct acceleration of electrons by a CO2 laser in a curved plasma waveguide, 2016, vol. 6, p. 28147 Search PubMed.
- L. Goldman, et al., Some Parameters of High Output CO2 Laser Experimental Surgery, Nature, 1970, 228(5278), 1344–1345 CrossRef CAS PubMed.
- C. K. N. Patel, Continuous-Wave Laser Action on Vibrational-Rotational Transitions of CO2, Phys. Rev., 1964, 136(5A), A1187–A1193 CrossRef.
- B. S. Yilbas, Comprehensive Materials Processing, Elsevier, Amsterdam, 2014, vol. 9, p. 5634 Search PubMed.
- D. Hülsenberg, et al., Silicate Glasses: A Class of Amorphous Materials, in Microstructuring of Glasses, Springer Berlin Heidelberg, Berlin, Heidelberg, 2008, pp. 3–56 Search PubMed.
- D. A. Coucheron, et al., Laser recrystallization and inscription of compositional microstructures in crystalline SiGe-core fibres, 2016, vol. 7, p. 13265 Search PubMed.
- J. Lawrence and L. Li, Modification of the wettability characteristics of polymethyl methacrylate (PMMA) by means of CO2, Nd:YAG, excimer and high power diode laser radiation, Mater. Sci. Eng., A, 2001, 303(1), 142–149 CrossRef.
- B. Temelkuran, et al., Wavelength-scalable hollow optical fibres with large photonic bandgaps for CO2 laser transmission, Nature, 2002, 420(6916), 650–653 CrossRef CAS PubMed.
- A. W. Ehler, High-energy ions from a CO2 laser-produced plasma, J. Appl. Phys., 1975, 46(6), 2464–2467 CrossRef CAS.
- X.-H. Lee, et al., Surface-structured diffuser by iterative down-size molding with glass sintering technology, Opt. Express, 2012, 20(6), 6135–6145 CrossRef PubMed.
- R. Bitterli, et al., Fabrication and characterization of linear diffusers based on concave micro lens arrays, Opt. Express, 2010, 18(13), 14251–14261 CrossRef PubMed.
- L. Eastham, LSD expands possibilities for beam shaping and optical control, in LEDs, LEDs & Lighting media group, UK, 2004 Search PubMed.
- T. R. Sales, et al., Light tamers, Photonics Spectra, 2004, 38, 58–65 Search PubMed.
- L. Ding, et al., Orthogonal Molecular Structure for Better Host Material in Blue Phosphorescence and Larger OLED White Lighting Panel, Adv. Funct. Mater., 2015, 25(4), 645–650 CrossRef CAS.
- Q. Zhao, et al., Printable Nanophotonic Devices via Holographic Laser Ablation, ACS Nano, 2015, 9(9), 9062–9069 CrossRef CAS PubMed.
- B. AlQattan, et al., Holographic direct pulsed laser writing of two-dimensional nanostructures, RSC Adv., 2016, 6(112), 111269–111275 RSC.
- J.-M. Guay, et al., Laser-induced plasmonic colours on metals, Nat. Commun., 2017, 8, 16095 CrossRef CAS PubMed.
- H. S. Lim and J. Yoo, FEM based simulation of the pulsed laser ablation process in nanosecond fields, J. Mech. Sci. Technol., 2011, 25(7), 1811 CrossRef.
- M. S. Brown and C. B. Arnold, Fundamentals of Laser-Material Interaction and Application to Multiscale Surface Modification, in Laser Precision Microfabrication, ed. K. Sugioka, M. Meunier and A. Piqué, Springer Berlin Heidelberg, Berlin, Heidelberg, 2010, p. 91–120 Search PubMed.
- M. Malinauskas, et al., Ultrafast laser processing of materials: from science to industry, Light: Sci. Appl., 2016, 5, e16133 CrossRef CAS.
- V. Malka, et al., Principles and applications of compact laser-plasma accelerators, Nat. Phys., 2008, 4(6), 447–453 CrossRef CAS.
- D. Hülsenberg, et al., Microstructuring Glasses Using Lasers, in Microstructuring of Glasses, Springer Berlin Heidelberg, Berlin, Heidelberg, 2008, pp. 175–196 Search PubMed.
- A. G. Kalampounias, et al., Influence of cw CO2-laser radiation on the amorphous-to-microcrystalline phase transition in a-Si:H films: a Raman spectroscopic study, Appl. Phys. A, 2014, 116(1), 303–310 CrossRef CAS.
- C. Huygens, Treatise on Light, Echo Library, Gloucestershire, 2007, pp. 139 Search PubMed.
- R. A. Barrio, et al., Regular ring dynamics in AX 2 tetrahedral glasses, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48(21), 15672–15689 CrossRef CAS.
- F. Domine and B. Piriou, Rarnan spectroscopic study of the SiOr-Al2O.-KrO vitreous system: distribution of silicon second neighbors, Am. Mineral., 1986, 71, 38–50 CAS.
- A. K. Yadav and P. Singh, A review of the structures of oxide glasses by Raman spectroscopy, RSC Adv., 2015, 5(83), 67583–67609 RSC.
- N. Umesaki, et al., Raman spectroscopic study of alkali silicate glasses and melts, J. Non-Cryst. Solids, 1996, 205, 225–230 CrossRef.
- T. Deschamps, et al., Soda-lime silicate glass under hydrostatic pressure and indentation: a micro-Raman study, J. Phys.: Condens. Matter, 2011, 23(3), 035402 CrossRef CAS PubMed.
- R. E. Prange and T.-W. Nee, Quantum Spectroscopy of the Low-Field Oscillations in the Surface Impedance, Phys. Rev., 1968, 168(3), 779–786 CrossRef CAS.
- Y. Montelongo, et al., Computer generated holograms for carbon nanotube arrays, Nanoscale, 2013, 5(10), 4217–4222 RSC.
- Y. Montelongo, et al., Plasmonic nanoparticle scattering for color holograms, Proc. Natl. Acad. Sci. U. S. A., 2014, 111(35), 12679–12683 CrossRef CAS PubMed.
- O. Katz, et al., Non-invasive single-shot imaging through scattering layers and around corners via speckle correlations, Nat. Photonics, 2014, 8(10), 784–790 CrossRef CAS.
- O. Katz, E. Small and Y. Silberberg, Looking around corners and through thin turbid layers in real time with scattered incoherent light, Nat. Photonics, 2012, 6(8), 549–553 CrossRef CAS.
- Z. K. Wang and H. Y. Zheng, Investigation on CO2 laser irradiation inducing glass strip peeling for microchannel formation, Biomicrofluidics, 2012, 6(1), 012820 CrossRef CAS PubMed.
- H. Y. Zheng and T. Lee, Studies of CO 2 laser peeling of glass substrates, J. Micromech. Microeng., 2005, 15(11), 2093 CrossRef CAS.
- Y. Yalikun, et al., An all-glass 12 [small mu ]m ultra-thin and flexible micro-fluidic chip fabricated by femtosecond laser processing, Lab Chip, 2016, 16(13), 2427–2433 RSC.
- T. Alqurashi, et al., Femtosecond laser ablation of transparent microphotonic devices and computer-generated holograms, Nanoscale, 2017, 9(36), 13808–13819 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8nr00529j |
| This journal is © The Royal Society of Chemistry 2018 |