Open Access Article
Open Access ArticleCommensurability between protein nanotubes in contractile ejection nanomachines
Sergey B.
Rochal
 *a,
Daria S.
Roshal
a,
Anna E.
Myasnikova
a and
Vladimir L.
Lorman
b
*a,
Daria S.
Roshal
a,
Anna E.
Myasnikova
a and
Vladimir L.
Lorman
b
aFaculty of Physics, Southern Federal University, 5 Zorge str., 344090 Rostov-on-Don, Russia. E-mail: rochal_s@yahoo.fr
bLaboratoire Charles Coulomb, UMR 5221 CNRS and Université de Montpellier, pl. E. Bataillon, 34095 Montpellier, France
First published on 4th December 2017
Abstract
Contractile ejection nanomachines being sheath–tube assemblies create an opening in the cell membrane to translocate molecules or ions across it. Here, on the most structurally investigated examples of the bacteriophage T4 tail and pyocin R2, we show that the rearrangement of the sheath structure resulting in its contraction and twist occurs in such a way that the contracted sheath becomes commensurate with the inner tube. This fact dictates the previously unknown simple geometrical relationship between the nanotube symmetries. Using the Frank and van der Merwe classical theory of commensurability, we study an interaction between two protein nanotubes forming such nanomachines and obtain an expression for the corresponding energy, which depends on the tube structures and their mutual arrangement. The appearance of commensurability between the contracted sheath and the inner tube decreases both the interaction energy and the total energy of the system. It improves the nanomachine efficiency, since the energy gain obtained increases the torque of the inner tube piercing the cell membrane.
Introduction
Among the most widely studied types of molecular nanomachines are contractile ejection systems.1–7 These nanomachines, which use a sheath–tube assembly to create an opening in the envelopes of target cells to translocate molecules or ions across lipid membranes, function due to a massive structural transformation involving the contraction of the sheath and the linear motion of the inner tube.6 Syringe-like molecular machines are especially widespread in the bacterial world.4,5,7,8 With the type VI secretion system (T6SS), Gram-negative bacteria can release toxins into the environment or into their prey.4,5,7 They also apply this system to translocate protein virulence factors into target eukaryotic cells and in intraspecific competition.4,5 Another kind of similar molecular machine for killing bacteria is synthesized by the bacteria themselves to kill competitors.9 These are the R-type pyocins produced by P. aeruginosa, which are unique because they do not inject any substance into the interior of the cell, but destroy it, making a hole in its shell and dissipating the cell's proton potential.6 Similar nanomachines are used by viruses selectively affecting bacterial cells.1–3,10 Using a syringe-like nanomachine located at the viral tail, bacteriophages inject into the cell their genetic material.1 Owing to their high killing capacity,11 R-type pyocins and bacteriophages have attracted attention for antimicrobial and bioengineering applications.12–14A significant breakthrough in the research of various biological nanomachines was induced by the methods of cryoelectron microscopy and X-ray crystallography,1,2,15 which in turn increased the scientific interest in these objects. Among the contractile ejection systems, the nanodevice of bacteriophage T4 is the most investigated. This bacteriophage attacking enterobacteria consists of a capsid containing viral DNA and a tail1 formed by a pair of coaxial cylinders of equal length. Both tail tubes are composed of M = 23 rings with 6 proteins per ring. Before intrusion into the host cell, the proteins of the outer envelope (so-called sheath) form loosely twisted spirals, and the tail has a so-called extended structure. Upon contact with the bacterium, the sheath changes its shape dramatically. Protein spirals are twisted more strongly and compressed. As a result, the outer shell decreases greatly in length, somewhat widens and turns into a more compact contracted structure. This leads to the piercing of the cell wall by the relatively rigid inner tail tube, which creates a pathway for the penetration of the viral DNA into the interior of the host cell.1 Despite the different functions, the structure of the bacteriophage T4 tail practically coincides with that of pyocin R2.6 Two nanoassemblies differ only in the number of rings (for pyocin M = 24) and have some variations in geometry (including the length and twist of protein spirals).
According to the recent structural data on the pyocin R2 assembly6 and the bacteriophage T4 tail,1 in both nanomachines the inner tube is commensurate with the extended outer one: the distance between the nearest rings and the turn angle between them are practically the same. This fact enforces us to raise a question whether the sheath contraction is a transition to another commensurate state of the sheath–tube system. The work of the syringe-like nanomachines is mainly produced at the expense of the internal energy stored in the extended sheath.1,6 However, the transition into the commensurate state would allow some increase of this work due to the additional decrease of the total energy of the system.
Modulated and commensurate systems are quite common in condensed matter physics.16 For example, such crystalline structures can be formed due to emerging sublattices17 or charge density waves,18 by the periodic distortion of one initial lattice,19 in magnetic systems.20 As we have recently shown,21 some commensurability is also possible in protein nanoassemblies, in particular, it occurs between two walls of the double-shelled spherical capsids of Reoviridae and Cystoviridae families and between concentric spherical sublattices forming the icosahedral capsids of some marine viruses, in which the capsid includes protruding knob-like proteins.
In this paper, using and generalizing the classical theory of commensurability, which is typical of modulated crystal structures,16 we show that in both the discussed nanomachines the commensurability between the outer and inner tubes reappears after the sheath contraction. Namely, the protein spirals of the outer tube contract and twist in such a way that they align along the larger diagonals of elementary cells forming the protein structure of the inner tube. Such structural organization of the contracted sheath reduces the energy of the interaction between the coaxial nanotubes and allows the increase of the torque created by the nanomachine.
Also, this paper studies an additional rational commensurability that is possible between the nanotubes of finite length. As we show here, if the distance between the nearest rings forming the inner tube is greater than the analogous one characterizing the outer tube, then some gain in the interaction energy can be achieved due to the appearance of the rational commensurability. It happens if the total length of the outer tube becomes equal to the half-integer number of distances between the rings in the inner tube. As we show here, this relationship exists between the total length of the contracted sheath and the distance between the rings in the inner tube of the bacteriophage T4 tail. However, the energy gain from this geometrical relationship is small, and in pyocin R2 there is no analogous rational commensurability.
Results and discussion
To begin with, below we study the commensurability and its features in the sheath–tube assembly of bacteriophage T4. As was already mentioned, both inner and outer tubes of this system are formed by ring-like hexamers consisting of N = 6 proteins. The contraction of the bacteriophage sheath starts from the baseplate and is realized by the successive flattening of neighboring hexamers. In addition, the turn angle δφ between the nearest hexamers changes and the sheath part, which is not yet contracted, rotates with respect to the inner tube as a whole. Thus, a front, which divides the initial and contracted sheath states, propagates along the tail.1,6,22 Note also that in the equilibrium contracted state the adjacent rings are turned by the angle δφ = 32.9° and are spaced from each other by the distance δz = 16.4 Å.2 Analogous parameters characterizing the structure of the inner tube,1δzin = 40.2 Å and δφin = 17.9°, practically coincide with those of the extended sheath, δzex = δzin, δφex = δφin, and the latter sheath structure is commensurate with the inner tube.Let us introduce a cylindrical coordinate system with the rotation angle φ and the z axis directed along the bacteriophage tail. Then the protein positions can be specified by two indices (n, m), where n = 0, 1, 2, ……, N − 1; m = 0, 1, 2, …, M − 1; M is the number of rings in the tube. In the contracted sheath tube the coordinates of the protein with indices (n, m) in a cylindrical coordinate system are
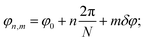 | (1a) |
| zn, m = z0 + mδz, | (1b) |
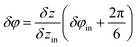 | (2) |
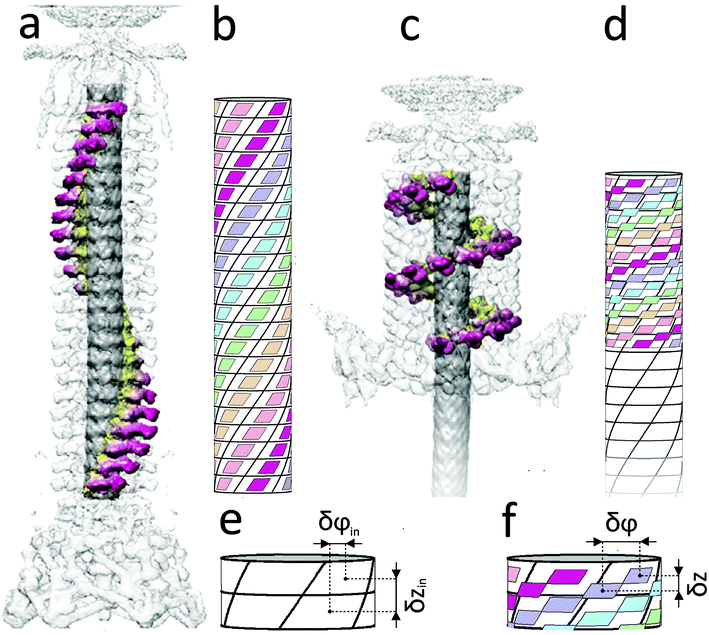 | ||
| Fig. 1 Extended (a, b) and contracted (c, d) states of the bacteriophage T4 tail. The panels (a, c) (modified from ref. 23, where these figures were constructed using the data from ref. 1) show the protein spiral in the extended and contracted states, accordingly. The elementary cells of the inner tube (see panels b, d) are shown by cylindrical parallelograms bounded with solid black lines. Each cell corresponds to one protein molecule of the inner tube. The protein helixes of the sheath are represented by small parallelograms whose centers coincide with the protein positions (see panels b, d). The sides of these parallelograms are parallel to the boundaries of the elementary cells drawn on the inner tube surface. In the extended state (a, b), the structures of the inner and outer tubes are commensurate and equivalent to each other: the centers of small and large parallelograms coincide. In the idealized contracted state (d), the protein helixes of the sheath are arranged along the diagonals of the inner tube elementary cells, and the length of the contracted sheath is exactly equal to the height of 9.5 cells drawn on the inner tube. Thin black circles show the upper and lower boundaries of the idealized sheath. The panels (e, f) demonstrate the definition of (δzin, δφin) and (δz, δφ) parameters for the inner tube and the contracted sheath, respectively. The parameters (δzex, δφex) of the extended sheath coincide1 with those of the internal tube. | ||
The proposed way to rationalize the contracted sheath arrangement is extremely accurate. The calculation of the δφ value according to eqn (2) yields 32.2°, while the structural work2 reports δφ = 32.9° and, as far as we know, this latter δφ value has not been revised in the subsequent studies.
The previously unknown but very simple commensurability relation (2) is not a single one for the bacteriophage T4 tail. According to the structural data for the outer2 and inner1 tubes, the total length of the contracted sheath 23δz turns out to be equal, with good accuracy, to the 9.5 times the distance between the neighboring rings in the inner tube. Indeed, the calculation of δz with the formula 9.5δzin/23 (δzin = 40.2 Å) yields δz = 16.6 Å instead of the actual value of 16.4 Å.2 This coincidence, in our opinion, is not accidental. It shows that an additional rational commensurability along the z-direction between the contracted sheath and the inner tube exists. This commensurability relationship is taken into account in idealized Fig. 1d and will be deduced below.
In order to understand the structural relationships between the sheath and the inner tube, we will develop further and apply the widely known model17 proposed by Frank and van der Merwe. In its initial form the model explains the commensurability appearance in a simple one-dimensional system. The system is a linear chain of particles located in an external periodic field. The particle energy in this field is 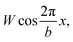 where W and b are the field's amplitude and period, respectively, and x stands for the particle coordinate. The neighboring particles of the chain are connected by springs and the model Hamiltonian is:
where W and b are the field's amplitude and period, respectively, and x stands for the particle coordinate. The neighboring particles of the chain are connected by springs and the model Hamiltonian is:
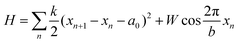 | (3) |
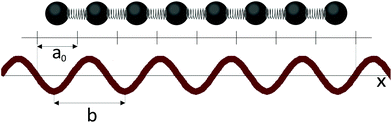
The minimization of (3) leads to a one-dimensional sine-Gordon equation that yields the equilibrium particle positions.24 When the parameters of the system, for example the equilibrium distance between particles a0 or period b, change, a sequence of phase transitions, called the devil's staircase, arises.16,17 The deepest minima of the Hamiltonian (3) correspond to the cases where the equilibrium distance between the nearest neighbors is an integer multiple of the distance between the minima of the periodic potential.
In the frames of the model17 one can also introduce a rational commensurability. Let us assume that all distances between the particles are equal to a0 (it occurs provided k ≫ W/b2) and, consequently, the particle coordinates are xn = a0n + Δ, where Δ is a constant. In this case only the second term in the energy (3) is non-zero and some specific relationships, which minimize the interaction of the chain fragment with the external field, exist. We refer to these relationships between b, a0 and Δ as those of rational commensurability. Fig. 2 shows an example of this commensurability between the external harmonic field and the chain fragment (8 particles located at the centers of 8 elementary cells). The shown chain fragment is 4.5 times longer than the period b and corresponds to 5 negative and 4 positive half-waves of the external field. It is easy to verify that the fragment's length and location are the most energetically favorable with respect to the periodic external field.
Note, however, that in the contracted state a gap of about 10 Å appears between the inner and outer nanotubes, and unlike the extended state, the direct contact between the nanotubes is absent. When modeling the sheath contraction, this fact is often used in order to neglect or to downplay the role of the sheath–tube interaction. For example, the authors of a recent report in ref. 25 do not consider this interaction at all during the construction of their model and argue at the end of the article that it can only increase the energy of the extended state. In contrast, we state that this interaction is much more important since both the inner and outer nanotubes are periodic structures formed from large structural units with the size of the same order as the gap between nanotubes. Due to the large dipole moments of such structural units6 they interact with each other at distances greater than the gap length. However, it is difficult to construct a microscopic approach explicitly taking into account the above-described electrostatic interaction between nanotubes. So, below we will generalize the theory17 and introduce a phenomenological potential determined by the structure of the inner rigid tube and model its influence upon the outer tunable sheath.
It is natural to assume that the minima of the desired interaction potential, reflecting the symmetry of the inner tube, coincide with the protein positions in the extended sheath, since the latter one is commensurate with the internal tubular structure. For the sake of simplicity, let us construct such simplest potential as a superposition of only two waves determined on the cylindrical surface.
As the first of them, it is reasonable to choose a planar wave with a period along the z direction equal to the distance between neighboring rings in the inner tube: V1 = −V10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(k1z), where
cos(k1z), where 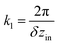 is the wave vector of this wave. To construct the second wave, let us recall that the protein positions of the inner tube like the positions (1) can be considered as located on a system of helical lines. Note also that there is an ambiguity in the choice of such a system since it is impossible to distinguish whether the neighboring hexamers are mutually turned by the angle δφin or by angles δφin + 2πq/N provided q is an integer and N = 6. So, one can use different systems of helical lines. The wave, whose troughs on the cylindrical surface form such a system with index q, is written as V2 = −V20
is the wave vector of this wave. To construct the second wave, let us recall that the protein positions of the inner tube like the positions (1) can be considered as located on a system of helical lines. Note also that there is an ambiguity in the choice of such a system since it is impossible to distinguish whether the neighboring hexamers are mutually turned by the angle δφin or by angles δφin + 2πq/N provided q is an integer and N = 6. So, one can use different systems of helical lines. The wave, whose troughs on the cylindrical surface form such a system with index q, is written as V2 = −V20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(k1z + Nφ), where
cos(k1z + Nφ), where 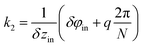 . Let us stress that for any q value the superposition of waves V1 and V2 has equivalent minima at the centers of the elementary cells drawn on the inner tube surface (see Fig. 1b and d), while it has maxima at the cells’ vertices. The horizontal boundaries of the cells are given by the troughs of the wave V1. Different q values correspond to different choices of the elementary cells. In particular, the ordinary cell tessellation shown in Fig. 1b and d is determined by q = 0. However, since the centers of elementary cells composing the contracted sheath are aligned along helical lines with q = 1 (see Fig. 1d), below we will use the wave with this q value to construct the desired phenomenological potential.
. Let us stress that for any q value the superposition of waves V1 and V2 has equivalent minima at the centers of the elementary cells drawn on the inner tube surface (see Fig. 1b and d), while it has maxima at the cells’ vertices. The horizontal boundaries of the cells are given by the troughs of the wave V1. Different q values correspond to different choices of the elementary cells. In particular, the ordinary cell tessellation shown in Fig. 1b and d is determined by q = 0. However, since the centers of elementary cells composing the contracted sheath are aligned along helical lines with q = 1 (see Fig. 1d), below we will use the wave with this q value to construct the desired phenomenological potential.
The consideration of the sheath contraction as a process and the discussion of the soliton-like6,22 boundary motion between the contracted and extended states of the outer tube are out of scope of this paper. Moreover, it should be emphasized that the nanomachine accomplishes work due to its internal energy, which is mainly stored in the extended sheath and is also not considered here. However, if the contracted sheath is characterized by such values of δφ and δz, which decrease the interaction energy between the inner tube and contracted sheath, an additional resulting energy gain can also be used when the nanomachine is activated. So, below we study only the energy Eint of the tube interaction, which is analogous to the second term in eqn (3):
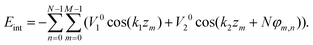 | (4) |
Since in the extended sheath state all the minima of the energy (4) simply coincide with the positions of sheath proteins, Eint in this state has the global minimum value Eint = −NM(V10 + V20). To calculate Eint for the contracted sheath, we substitute the protein coordinates (1) into the energy (4). Then the latter one becomes a function of the four variables φ0, z0, δφ, and δz with respect to which it should be minimized. Let us note that after the substitution of φ0 = z0k2 and eqn (2) into eqn (4), the second term in (4) takes its lowest possible value −V20NM. It is the energy gain due to the appearance of the commensurability (2). It occurs since the substituted equalities mean that all the protein positions are located in the troughs of the corresponding potential wave. Thus, eqn (4) becoming a function of two variables z0 and δz acquires the following form:
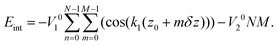 | (5) |
The above substitution does not fix the values of z0 and δz, which are the only variables determining the contribution of the first term (proportional to V10) into energies (4) and (5). Therefore, an additional energetically favorable relationship between δz, z0 and δzin can be found by the minimization of eqn (5). Using the Euler formula eiϕ = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ + i
ϕ + i![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ and summarizing the resulting geometric progression (its denominator is eik1δz) we obtain:
ϕ and summarizing the resulting geometric progression (its denominator is eik1δz) we obtain:
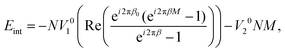 | (6) |
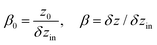 .
.
Note that the energy (6) could hypothetically take a globally minimal value if the sheath does not shorten during the nanomachine action, but elongates in such a way that the product k1δz would be a multiple of 2π. In this case in the global minima of (6) the variables β0 and β would be integers. However, in reality, the sheath contracts and such simple integer commensurability between the inner and outer tubes is not realized in the systems under consideration. So, below we investigate the local minima of the interaction energy (6), where the system can find itself if the more complex rational commensurability appears. For this purpose we rewrite the real part of the complex fraction in eqn (6) as:
| Re(ei2πβ0abs(Θ)eiγ), | (7) |
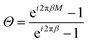 . Then, in the maxima of eqn (7), which correspond to the minima of eqn (6), ei2πβ0eiγ = 1 and eqn (7) is reduced to
. Then, in the maxima of eqn (7), which correspond to the minima of eqn (6), ei2πβ0eiγ = 1 and eqn (7) is reduced to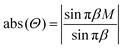 | (8) |
The minima of the function (8) with respect to the variable β are located at points β = j/M, where j = 1, 2, …, M − 1. Fig. 3 shows an example of such a function with M = 8. This value is equal to the number of particles which form the chain fragment shown in Fig. 2. The local maxima of eqn (8) lie in the midpoints between the local minima with high accuracy. Therefore in the local minima of the energy (6):
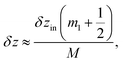 | (9a) |
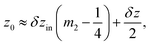 | (9b) |
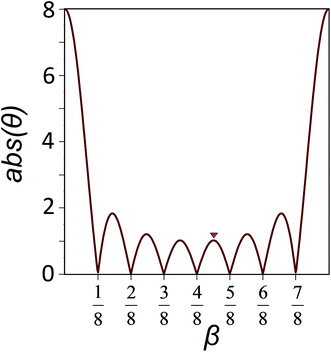 | ||
| Fig. 3 The dependence of abs(θ) on the β value. This function is used for the rigorous analysis of the rational commensurability between coaxial nanotubes. The function with M = 8 is shown. Its minima are located at the points 1/8, 2/8, …, 7/8. The red triangle marks the maximum (β ≈ 4.5/8) corresponding to the rationally commensurate state shown in Fig. 2. | ||
Let us stress that in the above part of the paper we have minimized not the total energy of the system, but only its part corresponding to the interaction between the nanotubes forming the nanomachines under consideration. As is well known, only the minimization of total free energy yields the equilibrium parameters of any system. The fact that in the bacteriophage case the minima of both energies practically coincide (with respect to variables δφ, δz) is very surprising and it can be explained only as the natural way to increase the nanomachine efficiency.
It should be noted that the appearance of the rational commensurability reduces the tube interaction energy by a value, which is proportional to NV10. At the same time, if the condition (2) is satisfied (and, consequently, the protein positions in the sheath are located along the larger diagonals of the inner tube elementary cells), then the gain in the interaction energy due to the commensurability (2) is V20NM, which is M times larger (provided V10 ≈ V20). Therefore, the rational commensurability is not very important for the considered systems.
Note also that since the condition (2) means that all positions of the contracted sheath are located in the troughs of one of the waves forming the tubes’ interaction potential, the condition (2) describes the ordinary multiple commensurability, which is widespread in classical objects studied in condensed matter physics. One can also say that it is the simplest commensurability since we used the wave with q = 1 and obtained the minimal rotation 2π/6 in eqn (2). In a more general case, the minimal angle 2π/6 in eqn (2) should be multiplied by an appropriate integer q.
Exactly the same commensurability (2) is manifested between the inner tube and the contracted sheath in pyocin R2. The structure of this contractile ejection nanomachine was recently studied in detail in ref. 6. Just like the tail of the bacteriophage T4, the syringe mechanism of pyocin R2 consists of two protein tubes; each of them, like in the bacteriophage case, is formed by six spirals. However, the number of rings in each of the tubes is 24 instead of 23. The tubes are commensurate in the precontracted state, where their common parameters6 are δzin≈ δzex≈ 38.4 Å and δφin ≈ δφex ≈ 18.3°. The parameters6 of the contracted sheath are δz = 16.2 Å and δφ = 33.1°. It is not difficult to verify that the protein spirals forming the structure of the contacted sheath are located approximately along the diagonals of the elementary cells composing the inner tube as it occurs in the bacteriophage T4. This fact indicates the commensurability existence. The usage of formula (2) yields an ‘ideal’ turn angle δφ = 33.03° for the contracted sheath, while the measured6 value is 33.1°. As distinct from commensurability (2), the rational commensurability between the contracted sheath and the inner tube being not very energetically profitable is absent in this system: 24δz/δzin ≈ 10.2.
In addition it should be noted that 10 years ago the sheath of the φKZ bacteriophage tail was investigated10 with comparatively low resolution and the symmetry of the internal tube was not determined. However, if in this bacteriophage, like in the both above-discussed systems, the extended sheath is commensurate with the internal tube, then, using the parameter values,10δzex ≈ 34.1 Å, δφex ≈ 22°, and δz ≈ 17.9 Å, one can apply eqn (2). For the contracted sheath it yields the turn angle δφ ≈ 37.8° instead of the reported10 one 36.7°. Thus, the structural study10 also confirms the theory suggested since the small angular deviation obtained is very likely associated with the insufficient study resolution.
Conclusions
In this paper, using the structural data on the bacteriophage T4 tail1,2 and pyocin R2 assembly,6 we investigated the commensurability between nanotubes forming syringe-like nanomachines and the commensurability influence on the nanomachine efficiency. The considered and similar nanodevices include two coaxial protein tubes, the outer one of which is tunable and can be in extended and contracted states. In both considered systems, as has been recently found,1,6 the inner tube is completely commensurate with the outer extended one. Here we show that after the sheath contraction a novel multiple commensurability arises between the nanotubes. The twisting of the sheath during its reconstruction occurs in such a way that the protein spirals forming the contracted sheath align along the diagonals of the inner tube elementary cells. In order to explain this finding, we developed the classic theory by Frank and van der Merwe17 and proposed a simple phenomenological potential, which describes the influence of the inner rigid tube upon the outer tunable one. Assuming that in the contracted sheath the neighboring protein rings are turned by the identical angle δφ and separated by the same distance δz, we minimized the interaction energy obtained and deduced the relationship between the δφ and δz variables and the analogous parameters characterizing the rigid inner tube. This simple relationship is satisfactory with a very good accuracy in both the considered systems.The extended state of the sheath is converted into the contracted one at the contraction front moving from the baseplate.1,2,22 At this boundary, the novel appearing commensurability minimizes the energy of the interaction between the inner tube and the contracted part of the outer one. So, at the contraction front the transformed and turned hexamer ring of the sheath falls into the minimum of the potential created by the inner tube that increases the torque between the tubes and, consequently, can be biologically expedient.
Along with the multiple commensurability, a less energetically profitable so-called rational commensurability can exist between the nanotubes of finite length. As we have shown, if the ring spacing δzin corresponding to the inner tube is greater than the analogous parameter δz of the sheath, then the rationally commensurate situation can be energetically favorable and it is realized provided that the total length of the outer tube Mδz is equal to the half-integer number of δzin values. In the tail of bacteriophage T4 this relationship (with the coefficient 9.5) exists, however, in pyocin R2 it is absent.
On the one hand, the results obtained in this work show the need for subsequent high resolution structural studies of syringe-like nanosystems and, on the other hand, our findings are important to understand and model the nanomachine action. With the exception of two systems considered in this paper, the geometric parameters of the other analogous nanodevices have not been sufficiently studied. The determination of these parameters for the type VI secretion system,4,5 the metamorphosis-associated contractile arrays26 and other similar objects would make it possible to understand better the general patterns that allow nature to increase the efficiency of contractile ejection nanomachines. In addition, our generalization of the theory17 for the tubular case could be developed further. As is known, solitons naturally appear in the classical version of this theory. Therefore, we believe that in the subsequent work it will be possible not only to consider the commensurability between the coaxial nanotubes in contractile ejection nanomachines, but also to construct a more adequate model of their action, which will describe the soliton-like motion of the boundary between the extended and contracted states of the outer tube.
Author contributions
V. L. proposed an idea that in both states of the bacteriophage T4 tail the protein nanotubes forming the tail are commensurate. After V.L.'s sudden death S. R. found the explicit form of this commensurability. He also wrote the greater part of the text. D. R. made the computations and drew the figures. A. M. participated in the discussion of the results and text writing.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors are grateful to Peter Leiman, who proposed to consider the example of pyocin R2 in this paper. S. R. and D. R. gratefully acknowledge the financial support of the Russian Science Foundation, grant number 15-12-10004.Notes and references
- N. M. Taylor, N. S. Prokhorov, R. C. Guerrero-Ferreira, M. M. Shneider, C. Browning, K. N. Goldie, H. Stahlberg and P. G. Leiman, Nature, 2016, 533, 346–352 CrossRef CAS PubMed.
- P. G. Leiman, P. R. Chipman, V. A. Kostyuchenko, V. V. Mesyanzhinov and M. G. Rossmann, Cell, 2004, 118, 419–429 CrossRef CAS PubMed.
- V. A. Kostyuchenko, P. R. Chipman, P. G. Leiman, F. Arisaka, V. V. Mesyanzhinov and M. G. Rossmann, Nat. Struct. Mol. Biol., 2005, 12, 810 CAS.
- M. Basler, M. Pilhofer, G. P. Henderson, G. J. Jensen and J. J. Mekalanos, Nature, 2012, 483, 182–186 CrossRef CAS PubMed.
- C. T. French, I. J. Toesca, T. H. Wu, T. Teslaa, S. M. Beaty, W. Wong, M. Liu, I. Schröder, P. Y. Chiou, M. A. Teitell and J. F. Miller, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 12095–12100 CrossRef CAS PubMed.
- P. Ge, D. Scholl, P. G. Leiman, X. Yu, J. F. Miller and Z. H. Zhou, Nat. Struct. Mol. Biol., 2015, 22, 377 CAS.
- G. Bönemann, A. Pietrosiuk and A. Mogk, Mol. Microbiol., 2010, 76, 815–821 CrossRef PubMed.
- A. B. Russell, S. B. Peterson and J. D. Mougous, Nat. Rev. Microbiol., 2014, 12, 137 CrossRef CAS PubMed.
- Y. Michel-Briand and C. Baysse, Biochimie, 2002, 84, 499–510 CrossRef CAS PubMed.
- A. Fokine, A. J. Battisti, V. D. Bowman, A. V. Efimov, L. P. Kurochkina, P. R. Chipman, V. V. Mesyanzhinov and M. G. Rossmann, Structure, 2007, 15, 1099–1104 CrossRef CAS PubMed.
- M. Kageyama, K. Ikeda and F. Egami, J. Biochem, 1964, 55, 59–64 CrossRef CAS PubMed.
- S. R. Williams, D. Gebhart, D. W. Martin and D. Scholl, Appl. Environ. Microbiol., 2008, 74, 3868–3876 CrossRef CAS PubMed.
- D. Scholl, M. Cooley, S. R. Williams, D. Gebhart, D. Martin, A. Bates and R. Mandrell, Antimicrob. Agents Chemother., 2009, 53, 3074–3080 CrossRef CAS PubMed.
- J. M. Ritchie, J. L. Greenwich, B. M. Davis, R. T. Bronson, D. Gebhart, S. R. Williams, D. Martin, D. Scholl and M. K. Waldor, Antimicrob. Agents Chemother., 2011, 55, 5469–5474 CrossRef CAS PubMed.
- S. Kanamaru, P. G. Leiman, V. A. Kostyuchenko, P. R. Chipman, V. V. Mesyanzhinov, F. Arisaka and M. G. Rossmann, Nature, 2002, 415, 553–557 CrossRef CAS PubMed.
- P. Bak, Rep. Prog. Phys., 1982, 45, 587 CrossRef.
- F. C. Frank and J. H. Van der Merwe, Proc. R. Soc. London, Ser. A, 1949, 198, 216 CrossRef CAS.
- J. A. Wilson, F. J. Di Salvo and S. Mahajan, Adv. Phys., 1975, 24, 117–201 CrossRef CAS.
- R. Pynn, Nature, 1979, 281, 433–437 CrossRef CAS.
- W. C. Koehler, Magnetic structures of rare earth metals and alloys, in Magnetic properties of rare earth metals, Springer, US, 1972, pp. 81–128 Search PubMed.
- S. B. Rochal, O. V. Konevtsova, A. E. Myasnikova and V. L. Lorman, Nanoscale, 2016, 8, 16976–16988 RSC.
- D. L. Caspar, Biophys. J., 1980, 32, 103–138 CrossRef CAS PubMed.
- M. Brackmann, S. Nazarov, J. Wang and M. Basler, Trends Cell Biol., 2017, 27, 623–632 CrossRef CAS PubMed.
- J. Rubinstein, J. Math. Phys., 1970, 11, 258–266 CrossRef.
- A. Maghsood, A. Chatterjee, I. Andricioaei and N. C. Perkins, Biophys. J., 2017, 113, 195–205 CrossRef PubMed.
- N. J. Shikuma, M. Pilhofer, G. L. Weiss, M. G. Hadfield, G. J. Jensen and D. K. Newman, Science, 2014, 343, 529–533 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2018 |