Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Hexanuclear iron(III) α-aminophosphonate: synthesis, structure, and magnetic properties of a molecular wheel†
Iaroslav
Doroshenko
 ab,
Michal
Babiak
ab,
Michal
Babiak
 ab,
Axel
Buchholz
ab,
Axel
Buchholz
 c,
Jiri
Tucek
c,
Jiri
Tucek
 d,
Winfried
Plass
d,
Winfried
Plass
 *c and
Jiri
Pinkas
*c and
Jiri
Pinkas
 *ab
*ab
aDepartment of Chemistry, Masaryk University, Kotlarska 2, CZ-61137 Brno, Czech Republic. E-mail: jpinkas@chemi.muni.cz
bCEITEC MU, Masaryk University, Kamenice 5, CZ-62500 Brno, Czech Republic
cInstitut für Anorganische und Analytische Chemie, Friedrich-Schiller-Universität Jena, Humboldtstraße 8, 07743 Jena, Germany. E-mail: sekr.plass@uni-jena.de
dRegional Centre of Advanced Technologies and Materials, Faculty of Science, Palacky University, Slechtitelu 27, CZ-78371 Olomouc, Czech Republic
First published on 12th January 2018
Abstract
A new hexanuclear molecular iron phosphonate complex, [Fe6(HAIPA)12(OH)6]·nH2O (1·nH2O) (H2AIPA = NH2(CH3)2CP(O)(OH)2, (2-aminopropan-2-yl)phosphonic acid), was synthesized from Fe2+ and Fe3+ salts in water by interaction with the ligand salts. Addition of corresponding amounts of sodium or tetramethylammonium salts of H2AIPA to the solution of iron precursors led to the formation of large bright-green crystals of complex 1. Isolated products were studied by spectroscopic and analytical methods – IR, Mössbauer spectroscopy, TG/DSC, ICP-OES, and CHN analysis. A novel {Fe6} hexanuclear molecular structure of 1 was confirmed by single crystal X-ray diffraction analysis. An octahedral coordination environment of iron cations is formed by phosphonate and hydroxo oxygens. Twelve phosphonate groups and six –OH groups act as bridging ligands and bind six Fe octahedra. Because of protonation of the amino group, the phosphonate anions coordinate in the zwitterionic form as HAIPA− (NH3+(CH3)2CPO32−). The iron cations are present in the form of high-spin Fe3+, which was confirmed by the bond valence sum (BVS) calculations and the 57Fe Mössbauer spectra. The magnetic measurements show antiferromagnetic coupling between the iron centers with decreasing temperature.
1 Introduction
The active study of metal phosphonate chemistry started from the middle of the previous century.1 Subsequently, the first layered zirconium phosphonate was obtained and investigated in the 1970s.2 A phosphonate group can potentially connect to nine metal centers by the three O donor atoms, and the bond strength of M–O–P is higher than that of M–O–C in carboxylates. This strong coordinating ability of phosphonate ligands results in the formation of different poorly soluble polymeric structures (chains, layers or networks).3 As a result, phosphonates have a wide range of applications in the synthesis of various metal–organic materials,4 catalysis,5–9 ion exchanging,10 and ion conducting materials.11,12 Molecular phosphonates have potential applications as precursors (building-blocks) for the synthesis of new organic–inorganic materials with predicted properties.13–15 However, due to the facile formation of polymeric structures, synthesizing molecular metal phosphonates is a challenging task. Usually there are two main synthetic strategies for their preparation. The first is addition of external non-phosphonate ligands to fill auxiliary coordination sites, which prevents the formation of polymeric structures. Another option is to use sterically demanding phosphonate ligands.16Molecular complexes of paramagnetic cations are very interesting objects due to their magnetic properties. Iron based molecules have been investigated in biological modeling studies.16–21 Polynuclear molecular iron phosphonates with nuclearities from {Fe4} to {Fe36} were reviewed recently.22–24 All these polynuclear molecular phosphonates contain Fe3+ ions. The corresponding reported hexanuclear {Fe6} cage molecules are based on three structural types, and all of them contain {Fe3O} triangular units.
In our study, the hexanuclear molecular iron phosphonate complex [Fe6(HAIPA)12(OH)6]·nH2O (1·nH2O) (H2AIPA = NH2(CH3)2CP(O)(OH)2, (2-aminopropan-2-yl)phosphonic acid) with a new structure was obtained without addition of any external ligand from an aqueous solution by the metathesis reaction between the sodium salt of (2-aminopropan-2-yl)phosphonic acid (H2AIPA) and iron salts. As the molecule of H2AIPA has an amino group, it crystallizes in the zwitterionic form as NH3+(CH3)2CP(O)(OH)O−. Coordination compounds of H2AIPA are potentially very interesting, because such complexes could find applications as molecular precursors to MOFs due to their stability and the presence of additional NH3+ groups. A polynuclear coordination compound of H2AIPA with aluminium was studied and reported previously by our group.25
2 Experimental
2.1 Materials and methods
Commercially available precursors FeCl3·6H2O, FeSO4·7H2O, NaOH, and (CH3)4NOH were used. H2AIPA was synthesized by the literature method26 from benzylcarbamate, acetone and phosphorus trichloride. IR spectra were recorded on a Bruker Tensor T27 spectrometer (4000–400 cm−1). KBr pellet and ATR (Bruker Platinum ATR) techniques were used. Thermogravimetric analysis (TG/DSC) was performed on a Netzsch STA 449C Jupiter apparatus over a temperature range of 25–1100 °C at a heating rate of 5 K min−1 and in the temperature range 25–1000 °C under a mixed atmosphere of 90% of nitrogen and 10% of synthetic air (70 cm3 min−1). The Fe, P and Na contents were measured on an ICP-OES spectrometer iCAP 6500 Duo (thermo, generator 27.12 MHz, amplitude 1.15 kW, plasma gas flow 12 dm3 min−1). Emission lines of 259.940 and 240.488 nm for Fe, 213.618 and 214.914 nm for P, and 588.995 and 589.952 nm for Na were used. Elemental analyses were carried out on Leco CHNS-932 and El Vario III elemental analyzers. Magnetic susceptibilities were measured for the ground polycrystalline sample using a Quantum Design MPMS-5 SQUID magnetometer. The measurements were performed with an applied field of 1000 and 2000 Oe in the temperature range of 2 to 300 K. The collected data were corrected for the diamagnetism of the sample holder, the capsula, and the diamagnetic contribution of the ligand. Transmission 57Fe Mössbauer spectra were recorded by employing a Mössbauer spectrometer operating at a constant acceleration mode and equipped with a 50 mCi 57Co(Rh) source. For low-temperature measurements, the samples were placed inside the chamber of a cryomagnetic system (Oxford Instruments, UK) to which a Mössbauer spectrometer is attached. For fitting the collected 57Fe Mössbauer spectra, the MossWinn software program was used. The isomer shift values were referenced to α-Fe at room temperature. Single crystal X-ray diffraction analysis was carried out on a Rigaku diffraction system (MicroMax-007 HF DW rotating anode source with a multilayer optic, partial χ axis goniometer, Saturn 724+ HG detector and Cryostream cooling device). Molybdenum Kα radiation (λ = 0.71075 Å) was used. The CrystalClear (Rigaku 2014) and CrysAlisPro (Agilent Technologies 2013) software packages were used for the data collection and data reduction. The structure was solved using the SHELXT program and refined (full matrix least-squares refinement on F2) using the SHELXL program. Powder X-ray diffraction analysis (PXRD) was performed on a GNR EUROPE XRD 600 diffractometer. Cobalt Kα radiation (λ = 1.7903 Å) was used (40 kV, 15 mA).2.2 Synthesis
Method A. A solution of H2AIPA (1.50 mmol, 0.235 g) and NaOH (1.50 mmol) in 30 cm3 of water was added to a solution of FeCl3·6H2O (0.500 mmol, 0.135 g) in 10 cm3 of water. After three days of standing in a closed vessel, bright green cube-like crystals were formed. The crystals were filtered off and washed with a small portion of cold water and dried in air. During drying, the crystals crumbled on evaporation of the crystal water. Yield 0.148 g (67.0%).
IR (KBr), ν, cm−1: 3424 (s), 1625 (m), 1514 (m), 1391 (w), 1371 (w), 1262 (w), 1121 (s), 1064 (vs), 988 (vs), 835 (w), 664 (m), 510 (m), 441 (w).
Elem., calcd (found) for [Fe6(HAIPA)12(OH)6]·31H2O (Mr(1·31H2O) = 2652.32 g mol−1), %: C, 16.30 (16.05); H, 6.70 (6.65); N, 6.34 (6.10); Fe, 12.63 (12.7); P, 14.01 (14.1); Na below detection limit.
The reaction was repeated with a larger amount of precursors: H2AIPA (6.00 mmol, 1.00 g), NaOH (6.00 mmol), FeCl3·6H2O (2.00 mmol, 0.540 g). Yield 0.708 g (80.1%).
Method B. A solution of H2AIPA (1.00 mmol, 0.157 g) and NaOH (1.00 mmol) in 20 cm3 of water was added to a solution of FeSO4·7H2O (0.500 mmol, 0.139 g) in 5 cm3 of water. After two days, green cube-like crystals were formed. After filtration, the product was washed with a small amount of cold water and dried in air. The crystals lost some amount of the crystal water, resulting in damage. Yield 0.066 g (29.3%).
IR (ATR), ν, cm−1: 3152 (m), 1607 (m), 1508 (m), 1467 (w), 1390 (w), 1369 (w), 1260 (w), 1110 (vs), 1060 (vs), 971 (vs), 834 (m), 656 (m), 500 (s), 428 (m).
Elem., calcd (found) for [Fe6(HAIPA)12(OH)6]·34H2O (Mr(1·34H2O) = 2706.35 g mol−1), %: C, 15.98 (16.10); H, 6.79 (6.10); N, 6.21 (6.08); Fe, 12.38 (12.7); P, 13.73 (13.68); Na below the detection limit.
The product yield could be increased by concentrating the mother liquor by evaporation. The reaction was repeated with a larger amount of the precursors: H2AIPA (31.8 mmol, 5.00 g), NaOH (31.8 mmol), FeSO4·7H2O (15.9 mmol, 4.420 g). Yield 5.182 g (72.3%).
The single crystals were grown in the reaction solution and taken for X-ray diffraction analysis directly from the mother liquor.
3 Results and discussion
3.1 Synthesis
(2-Aminopropan-2-yl)phosphonic acid (H2AIPA) was synthesized from benzylcarbamate, acetone and phosphorus trichloride by the literature method.26 H2AIPA crystallizes from water in a zwitterionic form as a monohydrate. The ligand identity was established by IR-, 1H, 31P{1H} NMR, ICP-OES spectroscopy, ESI-MS spectrometry, TG/DSC, and elemental analysis. Its molecular structure, which agreed with the literature studies,27,28 was confirmed by single crystal X-ray diffraction analysis.Because of the very low solubility of the ligand in organic solvents except methanol, all complexation reactions were carried out in water. The reaction of FeCl3·6H2O with three equivalents of the ligand sodium salt (NaHAIPA), which was formed by the dissolution of H2AIPA in water with one equivalent of NaOH, provides green cube-like crystals of [Fe6(HAIPA)12(OH)6] (1) upon standing for several days in a closed vessel. The same product was isolated from the reaction of FeSO4·7H2O with two equivalents of (NaHAIPA). Also, using a different base leads to the same product, as the synthesis was repeated with FeCl3·6H2O and (CH3)4NOH. The crystalline product has a large number of waters of crystallization, 30–44 per one molecule of 1. The water content in the dried product was calculated from the data obtained by TG/DSC, CHN and ICP-OES analysis. Qualitative tests for Fe2+ with 2,2′-bipyridil were negative on all samples of 1.
3.2 Crystal structure
The crystal structures of the free ligand, H2AIPA, and the obtained complex 1 were elucidated by single-crystal X-ray diffraction analysis.The molecular structure of H2AIPA was originally published in 198527 and later it was reinvestigated and intermolecular H-bonding was also discussed.28 The structural identity of H2AIPA was confirmed by our group during this work and previous studies.25
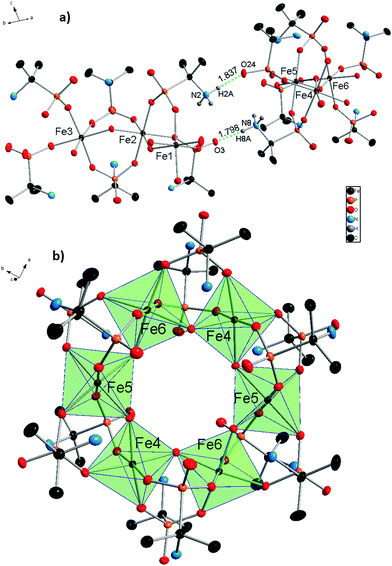
X-ray diffraction analysis of molecular iron phosphonate 1 was carried out for the crystals obtained by method A directly from the mother liquor. The identity of the two other samples of 1, synthesized by method B (see Experimental) and method A with NaOH replaced by (CH3)4NOH was confirmed by cell parameters comparison, powder X-ray diffraction analysis (Fig. S1 in the ESI†), and physico-chemical methods. The crystallographic data and the structure refinement parameters are shown in Table 1. The complex 1 crystallizes in the monoclinic crystal system (space group P21/c). The cyclic {Fe6} coordination clusters contain six iron cations connected by twelve bridging anionic HAIPA− ligands and six OH− groups. The asymmetric unit contains two halves of the complex 1 (three Fe atoms in each) that form two full molecules lying on special positions. This causes subtle differences between the geometries of the two crystallographically independent molecules. The selected bond lengths between nonequivalent iron cations and oxygen atoms are summarized in Table 2. The molecule of 1 possesses ideal D3d symmetry. The coordination environment of the iron centers in all cases is octahedral and formed exclusively by oxygen atoms. The two equatorial and two axial positions are filled by phosphonate oxygens and the two remaining equatorial positions are occupied by the bridging OH− groups in cis orientation. In the first independent unit (Fe1–3), the axial Fe–O distances are the longest of the six octahedral bonds, while the Fe–OH bridging distances are the shortest. This unit also has more regular Fe–O bonds than the second one (Fe4–6), possessing smaller differences between the longest and shortest distance in the octahedra. The iron centers connected by OH− bridges form the inner circle of the complex 1. Each phosphonate group binds two iron centers by two oxygen atoms. One phosphonate oxygen stays uncoordinated and takes part in the formation of H-bonds with the protonated amino groups. The six HAIPA− anions coordinate from each side of the molecular plane (Fig. 1). Their uncoordinated phosphoryl oxygens point alternately along the molecular C3 axis and along the horizontal plane. The amino groups alternate inside and outside of the molecular cavity. The hydrogen atoms of the internal amino groups form intramolecular H-bonds with both neighboring phosphonate oxygens (Fig. 2). Also, one hydrogen atom of the outer amino group, H9CN, forms an intramolecular H-bond with an outer phosphonate oxygen, O35, in the Fe4–6 independent part of the molecule. The eight outer amino groups in each molecule form intermolecular H-bonds with the outside pointing uncoordinated phosphonate oxygen atoms of the neighboring molecules (Fig. 1a). These intermolecular H-bonds connect independent molecules into the molecular sheets (Fig. S2 in the ESI†). The lengths and angles of the hydrogen bonds are presented in Table 3.
| 1 | |
|---|---|
| a Molecular formula and molecular weight include the six –OH hydrogen atoms not located in the crystal structure. | |
| Formula | C36H114Fe6N12O42P12a |
| fw (g mol−1) | 2094.14a |
| Cryst syst | Monoclinic |
| Space group | P21/c |
| a (Å) | 26.4924(3) |
| b (Å) | 17.3470(2) |
| c (Å) | 27.3768(3) |
| α (deg) | 90 |
| β (deg) | 106.530(1) |
| γ (deg) | 90 |
| V (Å3) | 12061.4(2) |
| Z | 4 |
| T (K) | 120 |
| δ calc. (g cm−3) | 1.150 |
| F(000) | 4320 |
| μ(Mo Kα) (mm−1) | 0.93 |
| θ range of data collection (deg) | 2.692–25.682 |
| Meased reflections | 68076 |
| Unique reflections (Rint) | 22874 (0.020) |
| No. of param. | 1009 |
| GOF on F2 | 1.058 |
| R 1 [I > 2σ(I)] | 0.0447 |
| wR2 (all data) | 0.1224 |
| Δρmax (e Å−3) | 0.88 |
| Δρmin (e Å−3) | −0.58 |
| Bond | Bond length, Å | S ij | n j | Bond | Bond length, Å | S ij | n j |
|---|---|---|---|---|---|---|---|
| a S ij = bond valence calculated by eqn (2). b n ij = atom valence calculated by eqn (1). | |||||||
| Fe1–O15i | 1.969 (2) | 0.56 | 3.03 | Fe4–O36ii | 1.983 (2) | 0.53 | 3.05 |
| Fe1–O1 | 1.972 (2) | 0.55 | Fe4–O39ii | 1.986 (2) | 0.53 | ||
| Fe1–O18i | 1.996 (2) | 0.51 | Fe4–O22 | 1.991 (2) | 0.52 | ||
| Fe1–O2 | 2.003 (2) | 0.50 | Fe4–O26 | 1.992 (2) | 0.52 | ||
| Fe1–O5 | 2.031 (2) | 0.46 | Fe4–O42ii | 2.016 (2) | 0.48 | ||
| Fe1–O21i | 2.037 (2) | 0.45 | Fe4–O23 | 2.023 (2) | 0.47 | ||
| Fe2–O1 | 1.969 (2) | 0.56 | 2.98 | Fe5–O25 | 1.964 (3) | 0.57 | 3.01 |
| Fe2–O8 | 1.990 (2) | 0.52 | Fe5–O29 | 1.965 (2) | 0.57 | ||
| Fe2–O4 | 1.994 (2) | 0.51 | Fe5–O22 | 1.982 (2) | 0.54 | ||
| Fe2–O12 | 2.004 (2) | 0.50 | Fe5–O33 | 2.012 (2) | 0.48 | ||
| Fe2–O7 | 2.031 (2) | 0.46 | Fe5–O28 | 2.047 (2) | 0.43 | ||
| Fe2–O9 | 2.044 (2) | 0.44 | Fe5–O30 | 2.050 (2) | 0.43 | ||
| Fe3–O16 | 1.976 (2) | 0.55 | 3.04 | Fe6–O29 | 1.973 (2) | 0.55 | 3.00 |
| Fe3–O15 | 1.979 (2) | 0.54 | Fe6–O36 | 1.975 (2) | 0.55 | ||
| Fe3–O14 | 1.993 (2) | 0.52 | Fe6–O37 | 1.996 (2) | 0.51 | ||
| Fe3–O8 | 1.999 (2) | 0.51 | Fe6–O32 | 2.020 (2) | 0.47 | ||
| Fe3–O11 | 2.023 (2) | 0.47 | Fe6–O35 | 2.020 (2) | 0.47 | ||
| Fe3–O19 | 2.028 (2) | 0.46 | Fe6–O40 | 2.040 (2) | 0.44 | ||
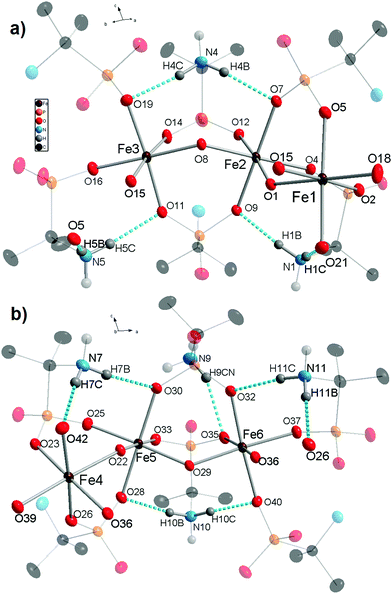 | ||
| Fig. 2 Asymmetrical fragments of the two independent molecules of 1 with Fe1, Fe2, and Fe3 atoms (a) and Fe4, Fe5, and Fe6 atoms (b). Intramolecular hydrogen bonds are represented by blue dashed lines, and their lengths are shown in Table 3. All atoms not taking part in the formation of the FeO6 polyhedra and the H-bonds were shaded for the sake of clarity. Thermal ellipsoids are drawn at the 50% probability level. | ||
| Bond | N–H, Å | H⋯O, Å | N⋯O, Å | ∠(N–H⋯O), deg. | |
|---|---|---|---|---|---|
| Intermolecular | N2–H2A⋯O24 | 0.911 | 1.837 | 2.737 | 168.99 |
| N8–H8A⋯O3 | 0.910 | 1.798 | 2.696 | 168.21 | |
| Intramolecular | N1–H1B⋯O9 | 0.910 | 1.947 | 2.854 | 174.73 |
| N1–H1C⋯O21 | 0.909 | 2.056 | 2.964 | 177.86 | |
| N4–H4B⋯O7 | 0.910 | 2.068 | 2.973 | 173.39 | |
| N4–H4C⋯O19 | 0.910 | 1.997 | 2.902 | 172.64 | |
| N5–H5B⋯O5 | 0.910 | 1.999 | 2.908 | 178.01 | |
| N5–H5C⋯O11 | 0.910 | 2.133 | 3.039 | 173.39 | |
| N7–H7B⋯O30 | 0.910 | 2.045 | 2.950 | 173.17 | |
| N7–H7C⋯O42 | 0.910 | 2.008 | 2.915 | 174.30 | |
| N9–H9CN⋯O35 | 0.911 | 2.336 | 3.183 | 154.53 | |
| N10–H10B⋯O28 | 0.912 | 2.047 | 2.846 | 173.86 | |
| N10–H10C⋯O40 | 0.909 | 1.940 | 2.955 | 174.33 | |
| N11–H11B⋯O26 | 0.911 | 1.986 | 2.897 | 179.15 | |
| N11–H11C⋯O32 | 0.909 | 2.089 | 2.993 | 172.62 | |
A large number of water molecules of crystallization are present in the crystal lattice. During the X-ray diffraction data processing, it was impossible to localize all the water oxygen atoms because of their thermal motions and positional disorder. The intermolecular electron density equal to 1374 electrons was removed by SQUEEZE. This value potentially represents 137.4 water molecules for one unit cell or 34.35 per one molecule of 1. The solvent accessible volume of one unit cell is 4841.5 Å3. The ratio of this value to the volume of one water molecule (0.0334 Å3) is equal to 161 H2O in the whole unit cell and 40.42 per one molecule of 1. Water content can be calculated relatively precisely for the dried product using the data obtained from auxiliary techniques, such as TG/DSC, ICP-OES, and CHN elemental analysis. The number of water molecules varies in the dried samples around 30–35 per one molecule of 1 and most probably depends on the environmental conditions.
Because of its diprotic nature, H2AIPA is able to form HAIPA− and AIPA2− anions. Therefore, both Fe3+ and Fe2+ oxidation states should be considered. The coordination sphere of all iron cations is formed exclusively by oxygen atoms and the oxidation states nj of the central atoms were evaluated by the BVS (bond valence sum) method using eqn ((1) and (2)).29,30
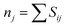 | (1) |
| Sij = exp[(R0 − rij)/B] | (2) |
3.3 Spectroscopy and thermal behavior
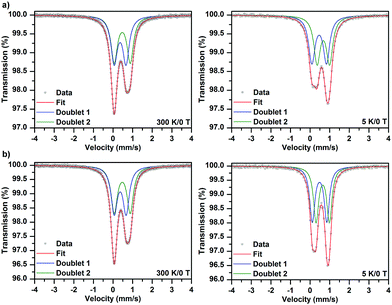
The 57Fe Mössbauer spectra of samples 1·31H2O and 1·34H2O measured at a temperature of 300 and 5 K, respectively, are depicted in Fig. 3. As can be clearly seen, the recorded 57Fe Mössbauer spectra show an asymmetric profile. As the texture effect and/or Goldanskii-Karyagin effect are highly improbable in this case, the asymmetry in the spectra implies the presence of more spectral components with distinct values of isomer shift (δ) and quadrupole splitting (ΔEq). At 300 K, the 57Fe Mössbauer spectra of both samples can be well fitted with two doublets (Fig. 3 and Table 4); the δ and ΔEq values fall in the interval typical for iron(III) in a high-spin state (i.e., S = 5/2) and with an octahedral coordination. Interestingly, the spectral ratio of the two doublet components amounts to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (Table 4). Thus, the presence of the two doublets can be ascribed to the two asymmetric units building the complex, most probably characterized by a slightly different ligand field. On lowering the temperature down to 5 K, the fitting model featuring the two doublet components with an equal spectral ratio matches well with the recorded 57Fe Mössbauer spectra of both 1·31H2O and 1·34H2O systems (Fig. 3 and Table 4). Upon decreasing the temperature, the ΔEq value was found to increase for one doublet while a reduction in the ΔEq parameter was observed for the other doublet component (Table 4). In order to explain the temperature dependence of the ΔEq parameter, contributions to the tensor of the electric field gradient must be considered. For complexes, lattice and valence electron terms play a crucial role; while the lattice contribution is most often temperature-independent, the valence electron contribution varies with temperature. Thus, the opposite temperature behavior of the ΔEq parameter for the two doublets can be explained in terms of different changes (i.e., magnitude and orientation) in the valence electron contribution of the Fe atoms in the two asymmetric units, which affects the probability of the presence of s-electrons in the Fe nucleus and hence the electric monopole interaction witnessed by the isomer shift. At the same time, the nature and type of bridging between the two asymmetric units are also believed to be responsible for the different orientational dependences of the electric field gradient evidenced by the two doublets.
1 (Table 4). Thus, the presence of the two doublets can be ascribed to the two asymmetric units building the complex, most probably characterized by a slightly different ligand field. On lowering the temperature down to 5 K, the fitting model featuring the two doublet components with an equal spectral ratio matches well with the recorded 57Fe Mössbauer spectra of both 1·31H2O and 1·34H2O systems (Fig. 3 and Table 4). Upon decreasing the temperature, the ΔEq value was found to increase for one doublet while a reduction in the ΔEq parameter was observed for the other doublet component (Table 4). In order to explain the temperature dependence of the ΔEq parameter, contributions to the tensor of the electric field gradient must be considered. For complexes, lattice and valence electron terms play a crucial role; while the lattice contribution is most often temperature-independent, the valence electron contribution varies with temperature. Thus, the opposite temperature behavior of the ΔEq parameter for the two doublets can be explained in terms of different changes (i.e., magnitude and orientation) in the valence electron contribution of the Fe atoms in the two asymmetric units, which affects the probability of the presence of s-electrons in the Fe nucleus and hence the electric monopole interaction witnessed by the isomer shift. At the same time, the nature and type of bridging between the two asymmetric units are also believed to be responsible for the different orientational dependences of the electric field gradient evidenced by the two doublets.
| Sample | T, K | Component | δ ± 0.01, mm s−1 | ΔEq ± 0.01, mm s−1 | Γ ± 0.01, mm s−1 | RA ± 1, % |
|---|---|---|---|---|---|---|
| 1·31H2O | 300 | D1 | 0.36 | 0.60 | 0.39 | 50 |
| D2 | 0.47 | 0.81 | 0.39 | 50 | ||
| 5 | D1 | 0.46 | 0.75 | 0.34 | 50 | |
| D2 | 0.67 | 0.64 | 0.34 | 50 | ||
| 1·34H2O | 300 | D1 | 0.37 | 0.61 | 0.38 | 50 |
| D2 | 0.47 | 0.82 | 0.38 | 50 | ||
| 5 | D1 | 0.48 | 0.74 | 0.32 | 50 | |
| D2 | 0.67 | 0.68 | 0.32 | 50 | ||
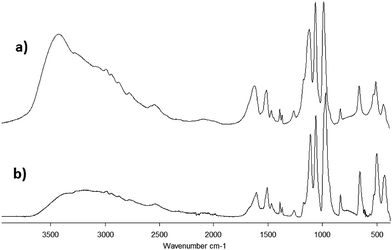
The IR spectra of both samples 1·31H2O and 1·34H2O are similar. Analogous to the spectra of the free ligand, the strongest absorption bands are located in the 1150–950 cm−1 region and correspond to the CPO3 group valence vibrations. An absorption band corresponding to the stretching vibrations of C–NH3+ could also be found in this region. The deformation vibrations of the CPO3 groups are located around 500 cm−1 (Fig. 4). The absorption bands at 1600 cm−1 most likely correspond to the deformation vibrations of the –NH3+ groups, while the absorption band corresponding to the deformation vibration of the –CH3 groups is observable near 1500 cm−1. Two low intensity bands near 1380 cm−1 probably correspond to the deformation vibrations of C(CH3)2.
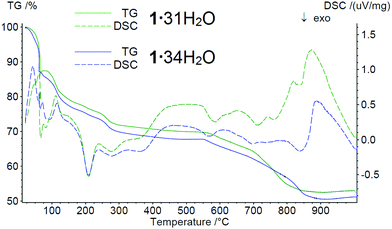
Thermogravimetric analysis was carried out under a low oxidation atmosphere of 90% N2 and 10% air to prevent rapid burning of the samples. The thermal behavior of the two samples 1·31H2O and 1·34H2O is very similar but we list resulting values for both of them. Endothermic evaporation of water is observed in two steps up to 160 °C with weight losses of 21.50 and 23.46%. From 160 °C to 230 °C, the first exothermic weight loss is observed (2.94 and 2.95%). Subsequently, exothermic weight loss (3.84 and 4.14%) is observed up to 310 °C. These two effects are most likely caused by oxidation of the organic groups. In the 310–925 °C temperature range, a continuous weight loss is accompanied by several exothermic events. The total weight losses in this temperature range are 19.01 and 18.94%. The exothermic peaks near 570, 700 and 830 °C are most likely formed by the combination of oxidation processes and crystallization of some phosphono–phosphate phases. The residues of the samples melted, forming a thin film at the bottom of the crucible. This is in good accordance with the intensive endothermic peaks at 870–880 °C, which most likely indicate the melting processes. The total weight losses are 47.06 and 48.85% for 1·31H2O and 1·34H2O, respectively (Fig. 5).
Thermogravimetric analysis of 1 obtained by method A with NaOH replaced by (CH3)4NOH was also repeated under an air atmosphere with heating up to 800 and 1000 °C. The thermograms are quite similar to the ones measured in the low oxidation atmosphere. The main differences are steeper and exothermic weight losses at 675–775 °C, which are explained by the faster and more intensive burning in air atmosphere. At 1000 °C, the residues of the sample also melted, forming a thin film in the crucible, while at 800 °C, a solid product was isolated. The powder X-ray diffraction analysis (PXRD) of this residue shows the presence of two main phases, Fe(PO3)3 (COD: 96-152-0967) and Fe3(P2O7)2 (COD: 96-403-0357) (Fig. S3 in the ESI†).
3.4 Magnetic properties
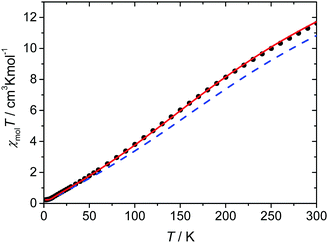
The magnetic susceptibility data of complex 1·31H2O were measured in the temperature range from 2 to 300 K. The magnetic data as a function of temperature are shown in Fig. 6. The χT value at 300 K is 11.6 cm3 K mol−1, which is significantly lower than the expected spin-only value for six independent high-spin iron(III) ions with S = 5/2 (26.25 cm3 K mol−1 for g = 2). Nevertheless, this value is much higher than the spin-only value expected for six independent low-spin iron(III) ions with S = 1/2 (2.25 cm3 K mol−1 for g = 2), supporting the results of the Mössbauer spectra that the majority of the iron(III) ions are in the high-spin state. On cooling, the χT value steadily decreases to reach values of nearly zero at temperatures below 5 K, indicating an overall antiferromagnetic coupling within the hexanuclear high-spin iron(III) ring system resulting in an S = 0 ground state and the presence of a small amount of paramagnetic impurity. Based on the crystal structure, two independent hexanuclear molecules are present in 1, where both in turn are composed of three crystallographically independent iron(III) ions. Therefore, at least three different coupling constants should be operative in each hexanuclear ring system. Unfortunately, the analysis of the spin system in terms of fitting appropriate coupling parameters to the experimental data using the standard software packages utilizing diagonalization of the full spin-Hamiltonian matrix is hampered by the large dimension of the resulting matrix.However, a well established magneto-structural correlation has been reported for dinuclear iron(III) complexes containing oxido, hydroxido, and alkoxido bridges utilizing the expression given in eqn (3),32 for which the coupling constant J for a pair of iron(III) ions is related to the average distance of the shortest Fe–O bridge (r) between them and the corresponding Fe–O–Fe angle (α).
J = A(B + C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) α + cos2 α + cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) α)exp(−Dr) α)exp(−Dr) | (3) |
Recently, Christou et al. proposed a new improved parameter set for eqn (3) that is especially validated for high-nuclearity iron(III) complexes (A = 2.46 × 109 cm−1, B = −0.12, C = 1.57, D = −8.99 Å−1 based on the Ĥ = −JŜ1Ŝ2 convention).36 The coupling constants calculated for the two independent hexanuclear molecules of 1 utilizing this magnetostructural correlation range from −29.0 to −36.6 cm−1 with an average value of −33.4 cm−1 and are summarized in Table 5. For the simulation of the experimental χT data, the coupling constants derived from the magnetostructural correlation of each of the two hexanuclear ring systems (Table 5) with subsequent averaging were employed. Although these lead to reasonably good agreement, the antiferromagnetic interactions are still somewhat overestimated (Fig. 6). It is tempting to take advantage of the rather small deviations between the individual coupling constants predicted by the magnetostructural correlation, as this suggests that a model based on six equal coupling constants might already be sufficient to describe the experimental magnetic data. In fact, the simulation with such a symmetric model with an average coupling constant of Jav = −30 cm−1, gives a good agreement with the experimental magnetic data, as observed in Fig. 6.
| r av, Å | α, deg | J, cm−1 | |
|---|---|---|---|
| Molecule 1 | |||
| Fe1–O1–Fe2 | 1.971 | 133.42 | −36.2 |
| Fe2–O8–Fe3 | 1.995 | 132.57 | −29.0 |
| Fe3–O15–Fe1 | 1.974 | 132.65 | −35.0 |
| Molecule 2 | |||
| Fe4–O22–Fe5 | 1.987 | 132.35 | −31.2 |
| Fe5–O29–Fe6 | 1.969 | 133.21 | −36.6 |
| Fe6–O36–Fe4 | 1.979 | 133.66 | −33.6 |
4 Conclusions
In conclusion, we have synthesized and structurally characterized a novel hexanuclear complex of iron(III) using (2-aminopropan-2-yl)phosphonic acid (H2AIPA) as the ligand and studied its spectroscopic, thermal, and magnetic properties by various physicochemical methods. The inorganic core is composed of six octahedral iron centers connected by bridging OH groups forming a wheel-like motif. The same molecular complex, [Fe6(HAIPA)12(OH)6]·nH2O, was synthesized from both Fe2+ and Fe3+ precursors. The presence of only the Fe3+ cations in the obtained products was confirmed by qualitative chemical analysis, bond valence sum calculation, magnetochemical analysis, and Mössbauer spectroscopy. The χT value at 300 K is in good agreement with the Mössbauer spectra, and shows the presence of Fe3+ in the high-spin state. On cooling, the χT value steadily decreases to reach nearly zero below 5 K, indicating an overall antiferromagnetic coupling within the hexanuclear iron(III) ring system resulting in an S = 0 ground state.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The results of this research have been acquired within the CEITEC 2020 (LQ1601) project with financial contribution made by the MEYS CR within special support paid from the National Program for Sustainability II funds. J. T. acknowledges the support from the MEYS CR under Project No. LO1305. CIISB research infrastructure project LM2015043 funded by the MEYS CR is gratefully acknowledged for the financial support for the measurements at the CF X-ray Diffraction and Bio-SAXS and the Josef Dadok National NMR Centre. The authors thank Dr M. Bittova for MS measurements, and Dr K. Novotny and L. Simonikova for ICP-OES analyses.References
- L. W. Daasch, J. Am. Chem. Soc., 1958, 80, 5301–5303 CrossRef CAS.
- G. Alberti, U. Costantino, S. Allulli and N. Tomassini, J. Inorg. Nucl. Chem., 1978, 40, 1113–1117 CrossRef CAS.
- A. Clearfield, Prog. Inorg. Chem., 1998, 47, 371–510 CAS.
- K. Maeda, Microporous Mesoporous Mater., 2004, 73, 47–55 CrossRef CAS.
- T. Y. Ma and S. Z. Qiao, ACS Catal., 2014, 4, 3847–3855 CrossRef CAS.
- Y.-P. Zhu, T.-Z. Ren and Z.-Y. Yuan, RSC Adv., 2015, 5, 7628–7636 RSC.
- S. He, X. Liu, H. Zhao, Y. Zhu and F. Zhang, J. Colloid Interface Sci., 2015, 437, 58–64 CrossRef CAS PubMed.
- G. a. Seisenbaeva, I. V. Melnyk, N. Hedin, Y. Chen, P. Eriksson, E. Trzop, Y. L. Zub and V. G. Kessler, RSC Adv., 2015, 5, 24575–24585 RSC.
- P. L. Llewellyn, M. Garcia-Rates, L. Gaberova, S. R. Miller, T. Devic, J. C. Lavalley, S. Bourrelly, E. Bloch, Y. Filinchuk, P. A. Wright, C. Serre, A. Vimont and G. Maurin, J. Phys. Chem. C, 2015, 119, 4208–4216 CAS.
- L. Jing, Y. Zhang, X. Li, X. He, J. Ma and L. Yang, J. Taiwan Inst. Chem. Eng., 2015, 56, 103–112 CrossRef CAS.
- G. Alberti and M. Casciola, Solid State Ionics, 1997, 97, 177–186 CrossRef CAS.
- P. Ramaswamy, N. E. Wong, B. S. Gelfand and G. K. H. Shimizu, J. Am. Chem. Soc., 2015, 7640–7643 CrossRef CAS PubMed.
- J. Chyba, Z. Moravec, M. Necas, S. Mathur and J. Pinkas, Inorg. Chem., 2014, 53, 3753–3762 CrossRef CAS PubMed.
- R. Murugavel, M. G. Walawalkar, M. Dan, H. W. Roesky and C. N. R. Rao, Acc. Chem. Res., 2004, 37, 763–774 CrossRef CAS PubMed.
- A. C. Kalita, N. Gogoi, R. Jangir, S. Kuppuswamy, M. G. Walawalkar and R. Murugavel, Inorg. Chem., 2014, 53, 8959–8969 CrossRef CAS PubMed.
- J. Goura, P. Bag, V. Mereacre, A. K. Powell and V. Chandrasekhar, Inorg. Chem., 2014, 53, 8147–8154 CrossRef CAS PubMed.
- S. Konar and A. Clearfield, Inorg. Chem., 2008, 47, 5573–5579 CrossRef CAS PubMed.
- R. Murugavel, N. Gogoi and R. Clérac, Inorg. Chem., 2009, 48, 646–651 CrossRef CAS PubMed.
- M. Mitra and R. Ghosh, Inorg. Chem. Commun., 2012, 24, 95–103 CrossRef CAS.
- E. M. Pineda, F. Tuna, Y. Z. Zheng, S. J. Teat, R. E. P. Winpenny, J. Schnack and E. J. L. McInnes, Inorg. Chem., 2014, 53, 3032–3038 CrossRef CAS PubMed.
- S. Konar, N. Bhuvanesh and A. Clearfield, J. Am. Chem. Soc., 2006, 128, 9604–9605 CrossRef CAS PubMed.
- C. M. Beavers, A. V. Prosverin, J. D. Cashion, K. R. Dunbar and A. F. Richards, Inorg. Chem., 2013, 52, 1670–1672 CrossRef CAS PubMed.
- J. Goura and V. Chandrasekhar, Chem. Rev., 2015, 115, 6854–6965 CrossRef CAS PubMed.
- J. A. Sheikh, H. S. Jena, A. Clearfield and S. Konar, Acc. Chem. Res., 2016, 49, 1093–1103 CrossRef CAS PubMed.
- J. Kratochvil, M. Necas, V. Petricek and J. Pinkas, Inorg. Chem., 2006, 45, 6562–6564 CrossRef CAS PubMed.
- J. Oleksyszyn, R. Tyka and P. Mastalerz, Synthesis, 1978, 479–480 CrossRef CAS.
- T. Glowiak, J. Crystallogr. Spectrosc. Res., 1985, 15, 173–180 CrossRef CAS.
- A. Bogomilova, G. Hägele, K. Troev, E. Wagner and M. Günther, Phosphorus, Sulfur Silicon Relat. Elem., 2012, 187, 165–180 CrossRef CAS.
- G. J. Palenik, Inorg. Chem., 2003, 42, 2725–2728 CrossRef CAS PubMed.
- I. D. Brown, Chem. Rev., 2009, 109, 6858–6919 CrossRef CAS PubMed.
- S. Z. Hu and Z. H. Zhou, Z. Kristallogr., 2004, 219, 614–620 CAS.
- H. Weihe and H. U. Güdel, J. Am. Chem. Soc., 1997, 119, 6539–6543 CrossRef CAS.
- C. Cañada Vilalta, T. A. O'Brien, E. K. Brechin, M. Pink, E. R. Davidson and G. Christou, Inorg. Chem., 2004, 43, 5505–5521 CrossRef PubMed.
- D. Plaul, E. T. Spielberg and W. Plass, Z. Anorg. Allg. Chem., 2010, 636, 1268–1274 CrossRef CAS.
- J. J. Borrás-Almenar, J. M. Clemente-Juan, E. Coronado and B. S. Tsukerblat, J. Comput. Chem., 2001, 22, 985–991 CrossRef.
- K. J. Mitchell, K. A. Abboud and G. Christou, Inorg. Chem., 2016, 55, 6597–6608 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 1567541. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7nj03606j |
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2018 |