Understanding charge transfer and recombination by interface engineering for improving the efficiency of PbS quantum dot solar cells†
Abstract
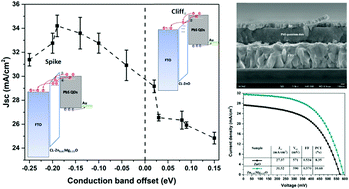
In quantum dot heterojunction solar cells (QDHSCs), the QD active layer absorbs sunlight and then transfers the photogenerated electrons to an electron-transport layer (ETL). It is generally believed that the conduction band minimum (CBM) of the ETL should be lower than that of the QDs to enable efficient charge transfer from the QDs to the collection electrode (here, FTO) through the ETL. However, by employing Mg-doped ZnO (Zn1−xMgxO) as a model ETL in PbS QDHSCs, we found that an ETL with a lower CBM is not necessary to realize efficient charge transfer in QDHSCs. The existence of shallow defect states in the Zn1−xMgxO ETL can serve as additional charge-transfer pathways. In addition, the conduction band offset (CBO) between the ETL and the QD absorber has been, for the first time, revealed to significantly affect interfacial recombination in QDHSCs. We demonstrate that a spike in the band structure at the ETL/QD interface is useful for suppressing interfacial recombination and improving the open-circuit voltage. By varying the Mg doping level in ZnO, we were able to tune the CBM, defect distribution and carrier concentration in the ETL, which play key roles in charge transfer and recombination and therefore the device performance. PbS QDHSCs based on the optimized Zn1−xMgxO ETL exhibited a high power conversion efficiency of 10.6%. Our findings provide important guidance for enhancing the photovoltaic performance of QD-based solar cells.
- This article is part of the themed collections: Quantum Dots: A Nanoscience Nobel Prize and International Year of the Periodic Table : From Pb and Sn Perovskites to the Next Generation


 Please wait while we load your content...
Please wait while we load your content...
