Electron transfer and exciplex chemistry of functionalized nanocarbons: effects of electronic coupling and donor dimerization
Tomokazu
Umeyama
 *a and
Hiroshi
Imahori
*a and
Hiroshi
Imahori
 *ab
*ab
aDepartment of Molecular Engineering, Graduate School of Engineering, Kyoto University, Nishikyo-ku, Kyoto 615-8510, Japan. E-mail: umeyama@scl.kyoto-u.ac.jp; imahori@scl.kyoto-u.ac.jp
bInstitute for Integrated Cell-Material Sciences (WPI-iCeMS), Kyoto University, Sakyo-ku, Kyoto 606-8501, Japan
First published on 12th March 2018
Abstract
In the past few decades, research on the construction of donor–bridge–acceptor linked systems capable of efficient photoinduced charge separation has fundamentally contributed to the fields of artificial photosynthesis and solar energy conversion. Specifically, the above systems are often fabricated by using carbon-based nanomaterials such as fullerenes, carbon nanotubes, and graphenes, offering limitless possibilities of tuning their optical and electronic properties. Accordingly, since understanding the structure–photodynamics relationships of π-aromatic donor–bridge–nanocarbon linked systems is crucial for extracting the full potential of nanocarbon materials, this review summarizes recent research on their photophysical properties featuring nanocarbon materials as electron acceptors. In particular, we highlight the electronic coupling effects on the photodynamics of donor–bridge–nanocarbon acceptor linked systems, together with the effects of donor dimerization. On a basis of their time-resolved spectroscopic data, the photodynamics of donor–bridge–nanocarbon acceptor linked systems is shown to be substantially influenced by the formation and decay of an exciplex state, i.e., an excited-state consisting of a π-molecular donor and a nanocarbon acceptor with partial charge-transfer character. Such basic information is essential for realizing future application of carbon-based nanomaterials in optoelectronic and energy conversion devices.
1. Introduction
In natural photosynthesis, especially in light-harvesting complexes and reaction centers, multistep energy transfer (EnT) and electron transfer (ET) reactions between well-arranged organic donor (D) and acceptor (A) pigments produce a long-lived charge-separated state in nearly 100% quantum yield, and thus allow to achieve eventual conversion of solar energy to chemical energy.1 The above processes have inspired the fabrication of artificial photosynthetic systems for use in solar fuels and photovoltaic devices; however, the structural complexity of natural photosynthetic systems necessitates the design and synthesis of simplified artificial analogues.2–7 Electron donors and acceptors are covalently or non-covalently linked with each other to perform the key steps of natural photosynthesis such as the highly efficient separation of photogenerated charges. In particular, covalently linked D–bridge (B)–A systems have received remarkable attention because of a better defined D–A geometry and elimination of the influence of complicated factors like D–A collisions in solution.Among the building blocks available for the construction of such D–B–A ensembles, fullerenes hold a prominent position as electron acceptors due to their excellent photophysical properties.8–19 For example, fullerenes exhibit a rigid and confined aromatic π-sphere structure, being able to accept up to six electrons. One-electron reduced fullerenes can also delocalize the charge over the spherical curved surface outside and inside with this unpaired electron stabilization, lowering the reorganization energy of ET processes. This behavior accounts for the acceleration of photoinduced charge separation (CS) and deceleration of charge recombination (CR) in fullerene-based D–B–A systems, as predicted by the Marcus theory of ET.8–19 Similar promises rest on one-dimensional (1D) and two-dimensional (2D) carbon nanostructures, i.e., single-walled carbon nanotubes (SWNTs) and graphenes. Sharing the sp2 carbon networks with fullerenes, SWNTs and graphenes have non-discrete structures with extraordinary mechanical, optical, and electronic properties.20–32 The continuous sp2 carbon networks of these nanostructures can be covalently functionalized, which allows their incorporation into D–B–A systems and simultaneously improves the processability of these otherwise poorly soluble materials.33,34
CS optimization has also spurred investigations of various kinds of electron donors (e.g., porphyrins, phthalocyanines, polyaromatic hydrocarbons, and π-conjugated oligomers). They are covalently linked to electron-accepting carbon nanostructures through a bridge,8–32 with hope to provide a wealth of information on the effects of the nature of the D and A units, electronic couplings (V), free energy change, reorganization energy, intervening solvent, and temperature. Various review articles8–32 including ours8–16,20,21 have been published on these topics, summarizing some important features of D–B–A ensembles containing carbon nanostructures as acceptor units. However, a deeper understanding of the relationship between the structure and photodynamics of π-aromatic donor–bridge–nanocarbon acceptor linked systems is still required for extracting the full potential of nanocarbon materials and extending their application scope.
Herein, we focus on our recent comprehensive studies35–38 and highlight the effects of D–A interaction (i.e., electronic coupling) on the photodynamics of D–B–A linked systems containing carbon nanostructures as acceptor units. Although the precise tuning of D–A electronic coupling is known to be essential for controlling the photodynamics,39–47 the electronic coupling effects on the photodynamics of nanocarbon-based photoactive composites have not been systematically addressed in detail prior to our work.35–38 We used oligo(p-arylene) (i.e., xylene or phenylene) as the bridge with straight rigid structures,48,49 to tune the D–A interaction finely and precisely by changing the number of aryl rings. Furthermore, we also summarize the effects of donor dimerization on the photodynamics of D–B–A linked systems containing SWNTs or graphenes as acceptor units.50–52 Dimer is a minimum unit to see the molecular interaction, but it is not straightforward to assess the effects of D–D or A–A dimer on their excited-state interaction between the D–D dimer and A or D and the A–A dimer. In bacterial photosynthetic reaction centers, the first CS event starts from a bacteriochlorophyll dimer, the so-called “special pair”.1 This unique structure has inspired synthetic chemists to mimic the dimer structure and the redox properties of the special pair to elucidate the intrinsic role in the CS event.2,53–61 However, the effects of donor dimerization on the photodynamics of donor-linked SWNT/graphene composites have never been scrutinized before due to the synthetic difficulty of accessing such composites. During the course of our study, we discovered the selective formation of donor dimers on SWNTs and graphenes by using aryl radical addition reactions.50–52 In this review article, we overview the photophysical properties of these uniquely designed systems to understand the structure–photodynamics relationships of covalently linked D–B–A systems with carbon nanostructures as acceptor units. The emphasis lies on the formation and decay of the exciplex state, an excited-state complex consisting of a π-molecular donor and a nanocarbon acceptor with partial charge-transfer (CT) character. In a simple CS reaction of D–B–A linked systems, the reactant state is the locally excited state of donor or acceptor (D*–B–A or D–B–A*) and the product state is the complete charge-separated state (D˙+–B–A˙−). However, when interaction between the donor and the acceptor is sufficiently strong, the exciplex can be rapidly produced.62,63 In the exciplex state, electron density is shared partially between the donor and acceptor units, forming (Dδ+–B–Aδ−)*. The exciplex sometimes appears as the precursor intermediate followed by formation of the complete charge-separated state, but the direct energy-wasting decay of the exciplex state to the ground state frequently happens.64 Although the precise understanding of the intrinsic nature of the exciplex state is crucial for efficient formation of the long-lived charge-separated state, the information is extremely limited in comparison with the complete charge-separated state because of lack of suitable model systems and difficulty in discovering such systems. The D–B–A linked systems with nanocarbons as acceptor units overviewed in this review are suitable models to give the insight into the exciplex states.
2. Effects of D–A electronic coupling on photodynamics
2.1. Photodynamics of D–B–A linked systems
Due to their facile synthesis, chemical stability, and excellent light-harvesting properties, porphyrin derivatives are one of the most frequently used electron donors in D–B–A linked systems,65,66 including a large number of porphyrin–fullerene analogues, mimicking photosynthetic CS and CR being available.8–32 It should be noted that the bridge structure in D–B–A ensembles exerts a profound influence on rate constants of CS and CR21 and affects the corresponding mechanisms (hopping versus tunneling).48 When the D–B energy gap is sufficiently small, the hopping mechanism is activated. In the tunneling mechanism, the transferred charge carriers have to tunnel in a single step through the barrier imposed by the bridge unit. The rate constants of tunneling-induced CS and CR (kCS and kCR, respectively) can be described as k0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(–βRee), where k0 is a kinetic prefactor, β is an attenuation factor, and Ree is the edge-to-edge separation distance between donor and acceptor.48,67–69 Namely, small β values correspond to long distances over which charges can be efficiently transferred. Generally, β values for CS and CR are dependent on bridge structures. For instance, β values for conjugated bridges (0.2–0.8 Å−1) are smaller than those for saturated hydrocarbon ones (0.8–1.0 Å−1), reflecting the weakly distance-dependent, molecular-wire nature of the conjugated bridges.
exp(–βRee), where k0 is a kinetic prefactor, β is an attenuation factor, and Ree is the edge-to-edge separation distance between donor and acceptor.48,67–69 Namely, small β values correspond to long distances over which charges can be efficiently transferred. Generally, β values for CS and CR are dependent on bridge structures. For instance, β values for conjugated bridges (0.2–0.8 Å−1) are smaller than those for saturated hydrocarbon ones (0.8–1.0 Å−1), reflecting the weakly distance-dependent, molecular-wire nature of the conjugated bridges.
Several groups have studied π-conjugated oligomers such as oligo(p-phenylene-vinylene), oligothiophene, and oligo(thienylene-vinylene) as bridge moieties to mediate electronic coupling between porphyrin and fullerene units,39–47 showing that these bridges allow efficient long-range ET with small β values, without forming the exciplex states. However, oligomeric π-conjugated bridges may exhibit a switch of the ET mechanism from tunneling to hopping at longer bridge length as the result of band gap narrowing by the π conjugation. To systematically investigate the effects of D–A electronic coupling on photodynamics without any influence of the π-conjugation degree of bridge units, the use of a rigid oligomer with a length-independent electronic structure is desirable.
2.2. Porphyrin–oligoarylene–fullerene linked systems
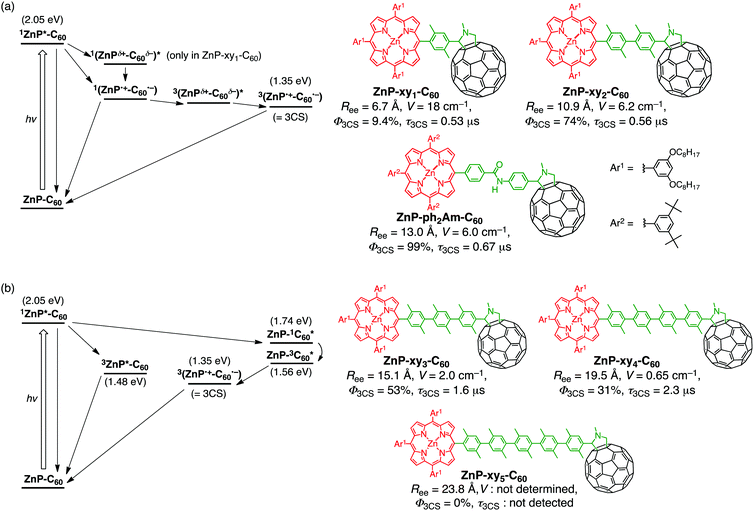
We employed oligo(p-xylene)s as the bridge units connecting zinc porphyrin (ZnP) and fullerene (C60) to prepare the dyads (ZnP–xyn–C60 (n = 1–5), Fig. 1).35 In the above bridges, the electronic conjugation of the benzene rings is almost nonexistent due to the significantly large (∼69°) equilibrium torsion angles between adjacent p-xylene units caused by steric hindrance.70,71 In addition, the rigid rod-shaped structure of these bridges enables fine length variation, with the edge-to-edge separation (Ree) of ZnP and C60, increasing by ∼4.2 Å per added xylene unit, from 6.7 Å for n = 1 to 23.8 Å for n = 5 (Fig. 2). To evaluate the effects of this separation in more detail, we also prepared ZnP–ph2Am–C60 with an Ree of 13.0 Å, lying between those of ZnP–xy2–C60 (10.9 Å) and ZnP–xy3–C60 (15.1 Å) (Fig. 2).39,72,73 The absorption spectra of ZnP–xyn–C60 (n = 1–5) and ZnP–ph2Am–C60 in benzonitrile (PhCN) could be well reproduced by a linear combination of those of porphyrin and fullerene references (ZnP–ref1 and C60–ref, Fig. 1). As expected, the π-conjugation effect through the oligoxylene bridges is completely suppressed and the ground-state electronic interaction between ZnP and C60 is negligible for all the dyads. Moreover, a decrease of the ZnP fluorescence by C60 in ZnP–xyn–C60 implies the existence of accelerated relaxation process of the porphyrin singlet excited-state (1ZnP*) by C60, e.g., ET, EnT, and/or exciplex formation. Indeed, the extent of fluorescence quenching in ZnP–xyn–C60 increases with decreasing Ree (>99% (n = 1), 95% (n = 2), 55% (n = 3), 30% (n = 4), and 5% (n = 5)), which is consistent with the distance-dependent decay of ZnP fluorescence quenching by C60 (vide infra).35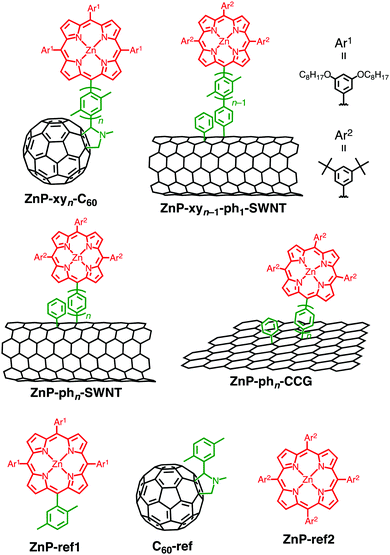 | ||
| Fig. 1 Structures of porphyrin–oligoarylene–carbon nanomaterial linked systems and reference compounds. | ||
The femto- to picosecond time-resolved transient absorption (TA) measurements of ZnP–xy2–C60 were performed by exciting the sample at the porphyrin Soret band. They reveal the formation of a spin-singlet charge-separated state (with a lifetime (τ) of 660 ps) exhibiting fingerprints of the ZnP radical cation (ZnP˙+) at 600–700 nm and of the C60 radical anion (C60˙−) at 1000 nm.35 Notably, nano- to microsecond time-resolved TA spectra demonstrated the unprecedented relaxation process of the spin-singlet charge-separated state: (i) the spin-singlet charge-separated state decays to the ground state or is converted into a triplet exciplex state, where the decay of the spin-singlet charge-separated state to the ground state is seemingly exclusive because the absorption of the triplet exciplex state is very close to that of the ground-state. (ii) The “spectroscopically transparent” triplet exciplex state is subsequently transformed with τ = 12 ns into a spin-triplet charge-separated state, followed by the decay to the ground state with τ = 560 ns. The above relaxation pathways are summarized in Fig. 2a. Considering the broader TA spectrum of the spin-singlet charge-separated state than the spin-triplet one, suggested is involvement of the exciplex character in the spin-singlet charge-separated state. Thus, the unidirectional conversion of the spin-singlet charge-separated state to the spin-triplet one via the triplet exciplex state may be explained by the plausible higher energy level of the spin-singlet charge-separated state than the spin-triplet one. The time-resolved electron paramagnetic resonance (EPR) spectroscopy complemented the relaxation pathway, in particular the important role of the spin–orbit coupling on the quick conversion of the spin-singlet charge-separated state to the triplet exciplex state, followed by the further transformation to yield the long-lived spin-triplet charge-separated state.35 The analogous behavior of the spin-singlet and spin-triplet charge-separated states was also observed in the TA spectra of ZnP–xy1–C60 and ZnP–ph2Am–C60, although the photoexcitation of ZnP–xy1–C60 resulted in a singlet exciplex being formed prior to the spin-singlet charge-separated state due to the stronger D–A electronic coupling originating from the short Ree, as we have already established before (Fig. 2a).21,39,64,74
Increasing the number of xylene units from n = 2 to n = 3 significantly affects the relaxation pathway, as summarized in Fig. 2b. Thus, ca. 50% of 1ZnP* undergoes intersystem crossing (ISC) to generate the triplet excited state (3ZnP*) that decays to the ground state without yielding the spin-triplet charge-separated state.35 In this case, the electronic coupling between 3ZnP* and C60 may be insufficient for CS owing to the ineffective π-orbital overlap between the planar porphyrin and xylene bridge caused by their orthogonal geometry. The rest of 1ZnP* contributes to EnT to C60, forming the corresponding singlet excited-state (1C60*). 1C60* undergoes ISC to yield the triplet excited-state (3C60*) that triggers ET from ZnP to 3C60* to generate the spin-triplet charge-separated state (Fig. 2b).35 Similar but less efficient EnT from 1ZnP* to C60, followed by ISC and ET from ZnP to 3C60*, was observed for ZnP–xy4–C60. Finally, the photodynamics of ZnP–xy5–C60 is almost the same as that of ZnP–ref1, which suggests little or no occurrence of CS and EnT in ZnP–xy5–C60. The gradual switch of the relaxation processes from 1ZnP* in the order of ET, EnT, and ISC can be rationalized by stronger distance dependence of ET than Förster-type EnT. On a basis of the rate constants obtained by TA analyses, the β value of ZnP–xyn–C60 (n = 1–5) was calculated as 0.52 Å−1, being comparable to the values previously reported for oligo(p-xylene) bridges.48
The quantum efficiency of the formation of the spin-triplet charge-separated state (Φ3CS) was estimated from the absorption intensity of C60˙− under the same conditions (Fig. 2).35 The Φ3CS value of ZnP–ph2Am–C60 was determined quantitatively by the photocatalytic oxidation of 1-benzyl-1,4-dihydronicotinamide by hexylviologen. The Φ3CS value dramatically increases with decreasing the electronic coupling (n = 1, 2), reaching a maximum of 99% for ZnP–ph2Am–C60,75 and gradually drops afterwards (n = 3–5). Remarkable is the bell-shaped dependence of these Φ3CS values as a function of the electronic coupling, highlighting the importance of modulating electronic coupling for CS efficiency optimization. This is in marked contrast with the dependence of the lifetime of the spin-triplet charge-separated state as a function of the electronic coupling where the τ value from submicrosecond to microsecond increases monotonically with decreasing the electronic coupling. Another important aspect of this study is the fast CR from the spin-singlet charge-separated state to the ground state, which conventionally has been interpreted by semi-classical Marcus theory for ET in the context of the strong vibration–ET coupling.76 Such spectroscopic behavior may be associated at least to some extent with the involvement of exciplex nature in spin-singlet charge-separated states as well as the evolution of the barely detectable triplet exciplex state, which governs the fate of relaxation from the spin-singlet charge-separated state, i.e., the direct decay to the ground state versus the generation of the spin-triplet charge-separated state via the triplet exciplex state.
2.3. Porphyrin–oligoarylene–SWNT linked systems
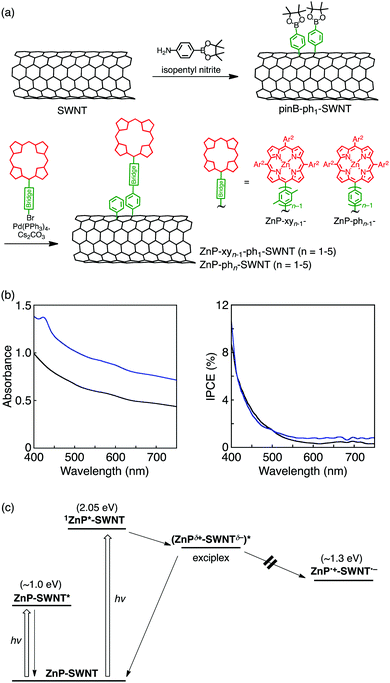
Chemical protocols for covalent SWNT functionalization can be largely divided into two categories.33,34 The first category involves the oxidation-assisted introduction of carboxy groups at the open ends and defect sites of SWNTs, followed by reactions with amines and alcohols to yield amide and ester linkages, respectively. The second approach is related to direct addition reactions to SWNT sidewalls, most of which correspond to the functionalization methods successfully employed in fullerene chemistry. Compared to the first method, the second one affords porphyrin–bridge–SWNT linked systems with robust and well-defined structures if the bridge unit introduced by the direct addition reactions is rationally designed. Therefore, the direct functionalization of SWNT sidewall by porphyrins is expected to contribute to a better understanding of the effect of electronic coupling on the photodynamics of porphyrin–bridge–SWNT linked systems. So far, covalently linked porphyrin–SWNT systems with various bridges have been constructed,77–81 with some of them being capable of forming the complete charge-separated state under illumination.79–81 However, in comparison with porphyrin–bridge–fullerene composites,8–32 the photodynamics of porphyrin–bridge–SWNT linked systems is extremely underexplored, and therefore, not much detailed information on the effects of bridge structure and length is available. Within this framework, our group envisioned the usage of oligo(p-xylene) bridges for porphyrin–bridge–SWNT linked systems (ZnP–xyn−1-ph1–SWNT (n = 1–5), Fig. 1).36Porphyrin–SWNT composites with oligo(p-xylene) bridges were prepared by two-step functionalization of SWNT with enriched chirality of semiconducting (6,5) produced by CoMoCAT method (average diameter of 0.8 nm) (Fig. 3a)36 to avoid the dimerization of porphyrin units on SWNT sidewalls (vide infra). First, SWNT sidewalls were functionalized with phenylpinacolborane groups utilizing a diazonium intermediate generated in situ from 4-aminophenylboronic acid pinacol ester and isopentyl nitrite to yield pinB–ph1–SWNT. Subsequently, Suzuki coupling between pinB–ph1–SWNT and porphyrin derivatives bearing oligo(p-xylene) with a terminal bromo group furnished porphyrin–SWNT linked systems with the oligo(p-xylene) bridge (ZnP–xyn−1-ph1–SWNT, n = 1–5). In view of the steric hindrance caused by the bottom part of the bridge being close to the SWNT, a phenylene unit was used instead of the xylene one. The absorption spectra of ZnP–xyn−1-ph1–SWNT (n = 1–5) in dimethylformamide (DMF) display an intense Soret band at 430 nm and weak Q-bands at 560 and 600 nm, together with a broad structureless absorption of SWNTs extending into the near-infrared region.36 The fluorescence spectra of ZnP–xyn−1-ph1–SWNT (n = 1–5) and ZnP–ref2 (Fig. 1) were measured by exciting at the Soret peaks where the porphyrin absorbances were adjusted to be identical. The porphyrin fluorescence in ZnP–xyn−1-ph1–SWNT (n = 1–5) is quenched intensively relative to that of ZnP–ref2 (>98%). This long-range efficient quenching of 1ZnP* by SWNTs in ZnP–xyn−1-ph1–SWNT through the oligo(p-xylene) bridges is in stark contrast with the short-range quenching of ZnP–xyn–C60 (e.g., only 5% fluorescence quenching in ZnP–xy5–C60 with the long bridge).35 This result implies that 1ZnP* can interact with 1D SWNTs more efficiently than zero-dimensional (0D) C60 through the bridge.
To shed light on the ultrafast photodynamic process, ZnP–xyn−1-ph1–SWNT (n = 1–5) were subjected to femto- to picosecond TA measurements, with simultaneous laser excitation of both porphyrin and SWNT moieties at 420 nm.36 The TA spectrum of ZnP–xy2-ph1–SWNT could be deconvoluted into four components with τ = 0.3, 1.1, 25, and 875 ps. On a basis of TA peak shapes as well as their fluorescence lifetimes, the first three components were assigned to SWNT excited-states (τ = 0.3 and 1.1 ps) and 1ZnP* (τ = 25 ps). Because ET from 1ZnP* to the conduction band of SWNTs is energetically favorable, the fourth component might be originated from the complete charge-separated state, i.e., the oxidized ZnP (ZnP˙+) and the reduced SWNTs (SWNT˙−). However, from the close comparison of the fourth component spectrum and electrochemical absorption spectra of ZnP˙+ and SWNT˙−, such an assignment can be ruled out. Then, the photoelectrochemical properties of ZnP–xy2-ph1–SWNT and pinB–ph1–SWNT were investigated using the electrophoretically deposited films on a nanostructured SnO2 electrode on FTO (denoted as FTO/SnO2/ZnP–xy2-ph1–SWNT and FTO/SnO2/pinB–ph1–SWNT).36 The incident photon-to-current efficiency (IPCE) spectrum of the FTO/SnO2/ZnP–xy2-ph1–SWNT electrode reveals a monotonously downward-sloping curve without the response of the Soret band of the porphyrin unit, although the absorption spectrum of FTO/SnO2/ZnP–xy2-ph1–SWNT exhibits the Soret band at 424 nm (Fig. 3b). This result indicates that the absorption arising from the porphyrin units does not generate the photocurrent, but one from the SWNT moiety solely generates the photocurrent in the FTO/SnO2/ZnP–xy2-ph1–SWNT device, as also seen in the devices with FTO/SnO2/pinB–ph1–SWNT (Fig. 3b). If EnT or ET from 1ZnP* to SWNT took place, the corresponding photocurrent response would be detected. Thus, the photoelectrochemical property of ZnP–xy2-ph1–SWNT indicates no occurrences of both EnT and ET from 1ZnP* to SWNT.
Considering the above results together with the preceding assignment associated with the exciplex formation in ZnP–C60 covalently linked systems,35,39,63,64 the fourth component observed in the TA spectrum of ZnP–xy2-ph1–SWNT can be attributed to an exciplex state that decays to the ground state without forming the complete charge-separated state (Fig. 3c).82 As contrasted with complete EnT and ET, the exciplex state formed by the interaction between 1ZnP* and SWNTs does not contribute to the photocurrent generation due to the partial CT character. One of the general features of the exciplex is red-shifted emission relative to those of the locally excited states of the individual chromophores. However, no exciplex emission of ZnP–xy2-ph1–SWNT was observed, indicating that the exciplex composed of ZnP and SWNT is nonemissive and decays to the ground state via vibronic relaxation pathways. This nonemissive character is the same as those of previously reported other porphyrin-linked fullerene systems.35,39,64 Furthermore, exciplex components were also observed for all the ZnP–xyn−1-ph1–SWNT (n = 1–5), although the exciplex lifetimes were dependent on bridge length.36 This finding demonstrates the exclusive formation of the exciplex state that directly decays to the ground state irrespective of the oligo(p-xylene) bridge length. Compared to ZnP–xyn–C60 with 0D C60 (n = 1–5), which yield the singlet exciplex state from 1ZnP* only in the case of n = 1,35 the strong interaction between 1ZnP* and 1D SWNTs via oligo(p-xylene) bridges allowed efficient bridge-mediated exciplex formation over a wide range of separation distances in ZnP–xyn−1-ph1–SWNT (n = 1–5).
The obtained TA data allowed us to determine rate constants for the formation and decay of the exciplex state (kFEX and kDEX, respectively), which exhibits exponential dependencies on Ree (edge-to-edge distance between ZnP and SWNT via the oligo(p-xylene) bridge). The slopes of the above plots, i.e., the β values for exciplex formation and decay in ZnP–xyn−1-ph1–SWNT (n = 1–5), were calculated as 0.12 and 0.14 Å−1, respectively, with these values being much smaller than those previously reported for CS and CR in D–B–A systems with oligo(p-xylene) bridges (0.5–0.8 Å−1).35,48,71 Such rather distance-independent character was attributed to the unique electronic structure of the exciplex with the partial CT character.
To study the effects of bridge conformation on the bridge-mediated interaction, ZnP and SWNTs were linked by oligo(p-phenylene) bridges (ZnP–phn–SWNT (n = 1–5), Fig. 1 and 3a).36 Benzene rings in oligo(p-phenylene) bridges are known to exhibit a more pronounced π conjugation than those in oligo(p-xylene) bridges, since the equilibrium torsion angle between adjacent phenylene units is smaller than that between the corresponding bulky xylene ones.48 The TA spectra of all the ZnP–phn–SWNT (n = 1–5) reveal the formation of the exciplex state, followed by its direct decay to the ground state without generating the complete charge-separated state (Fig. 3c). Moreover, the exponential dependencies of kFEX and kDEX on Ree in ZnP–phn–SWNT (n = 1–5) were unambiguously exemplified by the single logarithmic plots of ln(kFEX) vs. Ree and ln(kDEX) vs. Ree. Reflecting the more conjugated structure of oligo(p-phenylene), the β values for kFEX and kDEX (0.10 and 0.12 Å−1, respectively) in ZnP–phn–SWNT (n = 1–5) are slightly smaller than those in ZnP–xyn−1-ph1–SWNT (n = 1–5) (0.12 and 0.14 Å−1, respectively).36 This difference in the β values between ZnP–xyn−1-ph1–SWNT and ZnP–phn–SWNT systems supports that exciplex formation and decay occur via a through-bridge mechanism rather than via a through-space one. These unambiguous bridge length and conformation effects on the rate constants of bridge-mediated formation and decay of the exciplex state give a basis on the unique photodynamics of strongly electronically coupled D–B–A systems, wherein the exciplex state plays an essential role.
2.4. Porphyrin–oligoarylene–graphene linked systems
The sp2 carbon plane of graphene has also been decorated with porphyrins via covalent functionalization.83–87 To evaluate the effects of electronic coupling on their photodynamics, we covalently attached porphyrins onto the basal plane of chemically converted graphene (CCG) using an oligo(p-phenylene) spacer (ZnP–phn–CCG (n = 1–5), Fig. 1).37 Herein, CCG prepared by a chemical reduction of graphene oxide using hydrazine was used instead of graphene due to their graphene-like properties including transportation of charges.88 CCG is amenable to covalent functionalizations, and more importantly, is less expensive and easier to process than graphene. Such features of CCG render it a suitable model system for the photodynamics investigations. As in the case of ZnP–phn–SWNT,36 a series of ZnP–phn–CCG (n = 1–5) were prepared based on two-step functionalization: the attachment of phenylpinacolborane groups onto the CCG basal plane by the aryl addition reaction and the subsequent Suzuki coupling reaction between the porphyrins bearing the oligo(p-phenylene) bridge with a terminal bromo group and phenylpinacolborane-functionalized CCG (pinBph1–CCG). The absorption spectra in DMF are similar to the sum of those of ZnP–ref2 and pinB–ph1–CCG reference compounds. Notably, in comparison with the porphyrin–bridge–C60 linked system, enhanced fluorescence quenching of the ZnP moiety is observable:35 88% for ZnP–ph5–CCG and 5% for ZnP–xy5–C60. This result suggests that the excited ZnP interacts more intensively with 2D CCG than 0D C60. However, the quenching trend is suppressed considerably in ZnP–phn–CCG (n = 1–5) relative to ZnP–phn–SWNT:36 88% for ZnP–ph5–CCG and >98% for ZnP–phn–SWNT (n = 1–5), irrespective of the change from 1D SWNT to 2D CCG. This is counterintuitive, suggesting the alternation in the interaction between ZnP and CCG compared to that between ZnP and SWNT.The femto- to picosecond TA spectra of ZnP–phn–CCG (n = 1–5) were recorded at an excitation wavelength of 430 nm to allow the simultaneous excitation of both CCG and ZnP moieties.37 As a typical example, two components with τ of 0.3 and 40 ps were extracted from the TA data of ZnP–ph3–CCG. The analogy of the spectral shape and τ with those of reference CCG without the porphyrin moiety suggests that the shorter-lived component stems mainly from the CCG excited state. It should be noted here that CCG may function as both electron donor and acceptor in combination with ZnP because the oxidative excited-state of the ZnP unit is energetically higher than the conduction band of the functionalized CCG and the reductive excited-state of ZnP is lower than the valence band of the functionalized CCG.89–91 However, the broad spectral shape of the second component does not match with characteristic signals of the radical cation and anion of the porphyrin units. In addition, as in the case of ZnP–xyn−1-ph1–SWNT (n = 1–5),36 the absence of photocurrent response from porphyrin moieties in the photoelectrochemical device based on ZnP–ph3–CCG rules out the assignment of the longer component to 1ZnP* as well as the radical cation and anion. Therefore, the longer-lived component is safely attributed to an exciplex state, (ZnPδ+–CCGδ−)*. Similarity with the photodynamics of porphyrin–fullerene and porphyrin–SWNT linked systems reasonably excludes the possibility of the inverse exciplex, (ZnPδ−–CCGδ+)*.21,35,36,39,82 Furthermore, the exciplex components were also observed for all the ZnP–phn–CCG (n = 1–5), indicating that the exciplex state directly decays to the ground state without forming the complete charge-separated state irrespective of the bridge length (Fig. 4a).89–91 The exciplex formation from 1ZnP* to CCG is not detectable probably due to the ultrafast formation.37 This photodynamic behavior is almost identical to that of ZnP–phn–SWNT (n = 1–5),36 but notable is the difference in the dependence of the exciplex lifetime on bridge length. Namely, the exciplex lifetime of ZnP–phn–SWNT monotonically increases with increasing bridge length, whereas that of ZnP–phn–CCG does not follow the same proportional trend as a function of the bridge length: ZnP–ph1–CCG (33 ps) < ZnP–ph3–CCG (40 ps) < ZnP–ph2–CCG (42 ps) < ZnP–ph4–CCG (50 ps) < ZnP–ph5–CCG (59 ps). It is known that stronger electronic coupling results in shorter exciplex lifetimes.36,39 The switching of the τ values for ZnP–ph3–CCG and ZnP–ph2–CCG indicates the change in the decay mechanism of the exciplex state in terms of the bridge length. The decay process of the exciplex as the function of the number of the phenylene units was considered by through-bridge vs. through-space mediated mechanism.92 Indeed, the through-space electronic coupling between ZnP and CCG was shown to play a key role in the decay of the exciplex state to the ground state.
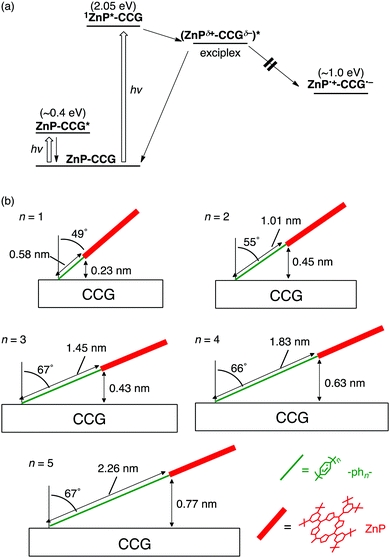 | ||
| Fig. 4 (a) Relaxation pathways of ZnP–phn–CCG (n = 1–5) in DMF. Energy levels of CCG are taken from literatures supposing that the covalent functionalizations by the aryl radical reaction would induce optical bandgaps of ca. 0.4 eV in the CCG moieties.89–91 (b) Schematic structures of ZnP–phn–CCG (n = 1–5) with the values of θ and through-space Ree estimated by AFM measurements. Through-bond Ree values are also shown. | ||
To support the hypothesis, the porphyrin-bridge geometry on CCG was evaluated by using atomic force microscopy (AFM). The thickness of ZnP–phn–CCG (n = 1–5) was determined within an error of ±0.1 nm, enabling us to precisely estimate the tilt angle (θ) of the rigid oligo(p-phenylene) bridges with respect to the surface normal and the Ree between ZnP and CCG (Fig. 4b). The θ value increases with increasing bridge length (n = 1–3), leveling off at 66–67° owing to the steric congestion around the bottom part of the phenylene unit and the attached CCG surface (n ≥ 3).37 The origin of the tendency on molecular tilt on 2D CCG as the function of bridge length is unclear, but it may result from special interaction between the ZnP–bridge and CCG. As a result, the direct through-space Ree value rises in the order of ZnP–ph1–CCG < ZnP–ph3–CCG < ZnP–ph2–CCG < ZnP–ph4–CCG < ZnP–ph5–CCG, which is in good agreement with the order of exciplex lifetime. The through-bond mechanism might contribute to the decay of the exciplex state to the ground state to some extent in ZnP–phn–CCG with the short bridges (n = 1, 2) because typically through-bond interaction is more efficient than through-space one. Nevertheless, the through-space mechanism rather than the through-bond one would be dominant in ZnP–phn–CCG, especially with the long bridges (n = 3–5) considering the short through-space distance relative to the long through-bond one. In accordance with the major contribution from the through-space mechanism, the rate constant of exciplex decay (kDEX) in ZnP–phn–CCG (n = 1–5) was exponentially dependent on the through-space Ree, with the corresponding β value calculated as 0.11 Å−1 being comparable to that of ZnP–phn–SWNT (0.12 Å−1).36 Such fundamental information on exciplex states, which can be addressed solely in the present well-defined ZnP–bridge–CCG system, provides deeper insights on the role of donor–graphene interaction in the excited-state.
2.5. Polythiophene–oligoarylene–C60 linked systems
Organic photovoltaics (OPVs) converting light into electricity generally comprise conjugated polymers as electron donors and fullerene derivatives as electron acceptors.93–97 Among the conjugated polymers, regioregular poly(3-hexylthiophene) (P3HT) is a prototypical donor in OPVs owing to its facile synthesis and good processability.98–100 The role of molecular environments in CS and CR processes of OPV-related materials can be unveiled by studying the photophysical properties of polymer–bridge–fullerene linked systems with well-defined structures and electronic interactions.101–104 To address the issue, we designed P3HT–bridge–fullerene linked systems (P3HT–phn–C60 (n = 0–3), Fig. 5a). An oligo(p-phenylene) bridge is used to tune the electronic coupling systematically, whereas the P3HT unit possesses a regioregular head-to-tail structure with high monodispersity (molecular weight distribution of ca. 5000). We examined their photodynamics based on time-resolved EPR spectra, fluorescence lifetimes, and nano- to microsecond time-resolved TA spectra in solution.38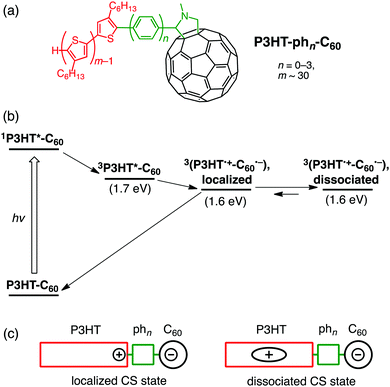 | ||
| Fig. 5 (a) Structures, (b) relaxation pathways in THF, and (c) schematic illustrations for localized and dissociated charge-separated states of P3HT–phn–C60 (n = 0–3). | ||
The relaxation pathways of P3HT–phn–C60 (n = 0–3) after excitation of the P3HT moiety at 532 nm are as follows (Fig. 5b).38 First, 3P3HT*–phn–C60 triplet excitons are dominantly generated from 1P3HT*–phn–C60 singlet excitons by ISC. Note that CS from 1P3HT*–phn–C60 does not take place efficiently because most of the singlet excitons cannot migrate to the terminal end connected to the bridge. Next, bridge-mediated intramolecular ET from the P3HT triplet state (3P3HT*) to C60 produces a localized charge-separated state (Fig. 5c) immediately after the triplet exciton reaches the next to the bridge during diffusion within the thiophene backbone. Similar to ZnP–xyn–C60 (n = 1–5),35 the exciplex state is not formed from 3P3HT* even in the case of short oligo(p-phenylene) bridges (n = 0, 1). In addition, no EnT from 3P3HT* to the C60 moiety was observed probably due to the stronger electronic coupling of oligo(p-phenylene) bridges than oligo(p-xylene) ones. Subsequently, charge dissociation gives rise to a dissociated charge-separated state (Fig. 5c) by overcoming the Coulomb binding energy. For all the P3HT–phn–C60 (n = 0–3), the rate constants of charge dissociation are on the order of ∼106 s−1, not being affected by bridge length. This implies that the entropy effect of disordered side chains in the P3HT moiety may be a major factor of influence for electron–hole dissociation. This thermodynamic dissociation mechanism is in remarkable contrast with the hot CT mechanism operating in conjugated polymer–fullerene bulk heterojunction (BHJ) blend films, where the vibrationally unrelaxed electron–hole pairs are generated on a timescale of <50 fs before completing the internal conversion of the excited polymer donor.105 Finally, the ground state of P3HT–phn–C60 (n = 0–3) is regenerated by CR. On a basis of the spin–spin exchange couplings (J), estimated by the spectral shapes of time-resolved EPR spectra,106 the V values for the CR processes were determined to be 3.7 and 2.9 cm−1 for P3HT–ph2–C60 and P3HT–ph3–C60, respectively, although the J and V values for P3HT–ph0–C60 and P3HT–ph1–C60 could not be estimated.107 In a BHJ blend film of P3HT and a typical fullerene acceptor, [6,6]-phenyl-C61-butyric acid methyl ester ([60]PCBM), V for CR was reported to be 0.2 cm−1.108 The larger V values in P3HT–ph2–C60 and P3HT–ph3–C60 highlight the role of the molecular environments on the efficient charge-dissociations by the BHJ films, where the P3HT polymer forms the π–π stacking crystalline phase.109 Meanwhile, the τ values of dissociated charge-separated states are essentially independent of bridge length (>4 μs in the presence of an external magnetic field for EPR measurements).38 Thus, the radical-pair deactivations are not governed by the primary CR kinetics of bridge-mediated electron tunneling, but by the diffusion of holes migrating within the conjugated polymer chains in the dyads. The present model is different from real systems of BHJ films with π–π stacking of conjugated polymers. Nevertheless, these unique molecular wire properties of the photogenerated charges in single molecules of the linearly arranged conjugated polymer–fullerene composites with the finely tuned electronic coupling may open a new door to the rational design of high-performance molecular electronics.
3. Effect of donor dimerization on photodynamics
3.1. Dimer formation on SWNT sidewalls
A fascinating feature of organic photoactive molecules is that their photophysical properties are altered by the degree of intermolecular interactions. Bearing this in mind, the photodynamics of donor–bridge–nanocarbon linked systems is expected to be modulated by controlling intermolecular interactions between donors as well as the electronic coupling. A dimer is the smallest molecular ensemble exhibiting photophysical properties different from the monomer. Actually, several artificial covalently and non-covalently assembled porphyrin dimer–fullerene systems have been constructed as a mimic of the “special pair” in natural photosynthesis,1 with the changes in the driving force and reorganization energy by the porphyrin dimerization, accelerating the photoinduced CS and decelerating CR.55,56,59,61SWNTs provide a number of reaction sites on their non-discrete 1D sp2 carbon network. However, studies of covalent sidewall modification with electron donors have mainly focused on donor–SWNT interactions.20–32,36 Intermolecular interactions between donors on SWNT sidewalls were ignored, since the donors were assumed to exist separately owing to their plausible random attachment and a low functionalization ratio (typically less than one donor unit per hundred carbons of the SWNT sidewall). To shed light on the effects of donor dimerization on donor–bridge–SWNT linked systems, a facile synthetic strategy is highly desirable. In this context, we paid attention to the addition reaction of highly reactive aryl radicals onto the sidewall,110,111 since this reaction was theoretically predicted to result in the attachment of two proximal aryl groups.112,113 The addition of a single aryl group with an unpaired electron is thought to activate carbon atoms near the addition sites, promoting the addition of a further aryl group thereon. More importantly, π–π interactions between donor units would accelerate their concerted or stepwise addition to form the corresponding donor dimer on the sidewall if we selected donors that were anticipated to show significant π–π interactions. Torres and coworkers recently reported a π–π interaction-directed functionalization approach to yield the regio-, stereo-, and atropselective products of untethered phthalocyanine dimer-linked [60]fullerene.59 However, such a strategy was applied only to fullerenes.
3.2. Pyrene dimer–SWNT linked systems
On a basis of the above hypothesis, the formation of pyrene dimers on SWNT sidewalls was attempted by the reaction between surfactant-wrapped SWNTs and 4-(1-pyrenyl)phenyl radicals produced from a diazonium salt (Fig. 6a).50 Herein, semiconductor-enriched SWNT produced by CoMoCAT method (average diameter of 0.8 nm) was employed. Pyrene, a simple polycyclic aromatic hydrocarbon, was utilized with hope that the π–π interaction would accelerate the dimer formation. Indeed, the UV-vis absorption of pyrene dimers is known to be different from that of the monomer and changed characteristically depending on their separation distance and mutual orientation.114,115 To our surprise, the obtained product showed a new broad absorption band at 450 nm with an intensity comparable to that of the pyrene π–π* band at 350 nm, suggesting the formation of pyrene dimer-linked SWNTs ((Py–ph1)2–SWNT, Fig. 6a). In accordance with this assignment, high-resolution transmission electron microscopy (HR-TEM) images allowed us to determine the precise structure of the pyrene dimers attached to the SWNT sidewall in (Py–ph1)2–SWNT.50 The UV-vis absorption spectrum is in good agreement with that calculated from the observed dimer structure, where the pyrene planes are separated by van der Waals contact with an orientation angle of ca. 65°. Thus, the present methodology of forming and probing molecular dimers on SWNT sidewalls looks promising to elucidate close structure–property relationships existing within the dimeric molecules of interest, which is selectively prepared by the one-step functionalization.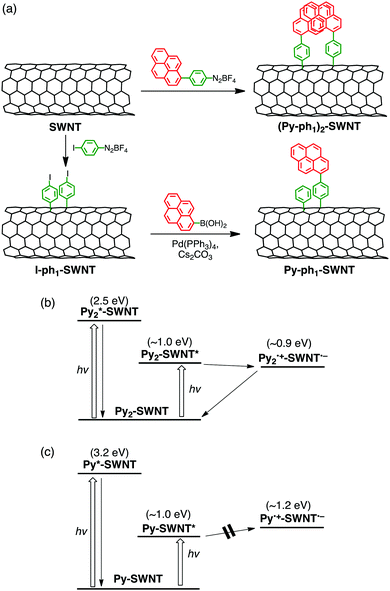 | ||
| Fig. 6 (a) Synthetic scheme and relaxation pathways of (b) (Py–ph1)2–SWNT and (c) Py–ph1–SWNT in DMF. Energy levels of SWNT are based on (6,5)-chirality. | ||
As in the case of ZnP–xyn−1-ph1–SWNT (n = 1–5), monomeric pyrene-linked SWNTs (Py–ph1–SWNT) were selectively prepared by two-step functionalization (Fig. 6a).50 In the first step, the sidewalls of SWNTs were functionalized with p-iodophenyl groups using a diazonium salt to yield I–ph1–SWNT, which was followed by Suzuki coupling with pyrenylboronic acid (coupling reaction yield ≈9%). Although p-iodophenyl groups in I–ph1–SWNT might form dimeric structures on SWNTs, the low yield of the Suzuki coupling excluded the formation of the pyrene dimer in Py–ph1–SWNT. In fact, the UV-vis absorption spectrum of Py–ph1–SWNT is a linear combination of the sum of those of I–ph1–SWNT and 1-phenylpyrene references, confirming the selective formation of the pyrene monomers on SWNTs by using the two-step functionalization (vide supra).
The femto- to picosecond TA spectrum of (Py–ph1)2–SWNT was recorded in DMF at an excitation wavelength of 350 nm where both pyrene and SWNT moieties were excited. ET occurs from the ground-state pyrene dimer to the excited-state SWNT, yielding the pyrene dimer radical cation and the SWNT radical anion with a rate constant of ∼30 ps (Fig. 6b).50 Meanwhile, the monomeric excited-state pyrene in Py–ph1–SWNT is rapidly quenched by the SWNT, possibly generating the SWNT excited state via EnT within the time resolution of the measurement system (∼0.15 ps). The π–π interaction between the pyrene units lifts the energy level of the highest occupied molecular orbital (HOMO), making it possible to drive exothermic ET from the dimeric pyrenes to the excited SWNT in (Py–ph1)2–SWNT. On the other hand, ET from the monomeric pyrenes to the excited SWNT in Py–ph1–SWNT remains energetically unfavorable considering the lower HOMO level of the monomeric pyrene than the energy level of the reductive SWNT excited state. In sharp contrast to exclusive exciplex formation and decay of ZnP–ph1–SWNT,36 (Py–ph1)2–SWNT did not form the exciplex state irrespective of the same short phenylene bridge. This may result from the weaker electronic coupling with small π pyrene than large π porphyrin. Nevertheless, the difference in intermolecular interactions of donors between (Py–ph1)2–SWNT and Py–ph1–SWNT has a profound influence on their photodynamics.
3.3. Pyrene dimer–graphene linked systems
The same methodology was applied to pyrene–graphene systems.51 The one-step reaction between the graphene plane of CCG and the 4-(1-pyrenyl)phenyl radical, in situ generated from the corresponding diazonium salt, yielded a CCG-bound pyrene dimer ((Py–ph1)2–CCG, Fig. 7a).51 The dimer formation was confirmed by the appearance of the additional absorption band at 450 nm. Meanwhile, the two-step method led to the attachment of monomeric pyrene to CCG (Py–ph1–CCG, Fig. 7b). Femto- to picosecond TA spectra of (Py–ph1)2–CCG and Py–ph1–CCG were recorded in DMF. The photoexcitation of (Py–ph1)2–CCG results in the formation of the exciplex state (τ = 19 ps) that subsequently is converted to the complete charge-separated state (τ > 6 ns) (Fig. 7c). In contrast, the photoexcitation of Py–ph1–CCG leads to the sole formation of the exciplex state (τ = 41 ps) that directly decays to the ground state without forming the complete charge-separated state (Fig. 7d). Both (Py–ph1)2–CCG and Py–ph1–CCG possessing the same short phenylene bridge form the exciplex state upon photoexcitation, suggesting that pyrene interacts with 2D CCG more effectively than 1D SWNT.50 Strikingly, the dimerization of pyrene on CCG enables the formation of the complete charge-separated state following the exciplex state in (Py–ph1)2–CCG,51 in partial analogy with the occurrence of photoinduced ET in (Py–ph1)2–SWNT.50 However, the difference in the photodynamics of (Py–ph1)2–CCG and Py–ph1–CCG cannot be rationalized simply by the differences between the HOMO energy levels of the pyrene monomer and dimer, since the oxidative excited states of both pyrene monomer and dimer are much higher in energy than the CCG conduction band.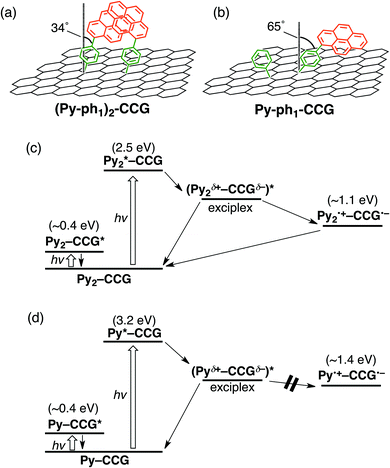 | ||
| Fig. 7 Structures of (a) (Py–ph1)2–CCG and (b) Py–ph1–CCG with the values of θ determined by AFM measurements. The though-space Ree values of (Py–ph1)2–CCG and Py–ph1–CCG are estimated to be 0.41 nm and ∼0 nm, respectively. Relaxation pathways of (c) (Py–ph1)2–CCG and (d) Py–ph1–CCG in DMF. Energy levels of CCG are taken from literatures supposing that the covalent functionalizations by the aryl radical reaction would induce optical bandgaps of ca. 0.4 eV in the CCG moieties.87–89 | ||
To throw light on the origin of differences between the photodynamics of (Py–ph1)2–CCG and Py–ph1–CCG, we scrutinized the pyrene geometry on CCG by using AFM, as described for ZnP–phn–CCG (n = 1–5).37 The θ values for (Py–ph1)2–CCG and Py–ph1–CCG were determined as ∼34° and ∼65°, respectively. Accordingly, the direct through-space edge-to-edge distance between pyrene and CCG in Py–ph1–CCG is shorter than that in (Py–ph1)2–CCG (Fig. 7a and b). Therefore, the photodynamics of (Py–ph1)2–CCG and Py–ph1–CCG can be explained as follows. The CCG-bound pyrene monomers in Py–ph1–CCG are more steeply tilted with respect to the CCG basal plane. Thus, the enhanced through-space electronic coupling in Py–ph1–CCG would lead to the exclusive formation and decay of the exciplex state. In contrast, the pyrene dimerization with the double anchoring onto CCG in (Py–ph1)2–CCG inhibits the above tilt, reducing the electronic coupling compared to Py–ph1–CCG. Consequently, the initial formation of the exciplex state, followed by conversion to the complete charge-separated state would take place, as seen in ZnP–xy1–C60. Tuning D–A electronic coupling by controlling intermolecular interactions between donors may become a new strategy for the rational design of π-aromatic compound–2D nanostructure linked systems.
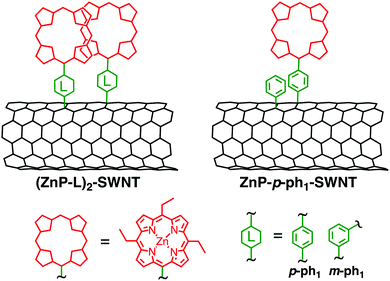
3.4. Porphyrin dimer–SWNT linked systems
The successful formation of pyrene dimers on SWNT and CCG encouraged us to apply the same methodology to porphyrin–SWNT systems, as shown in Fig. 8.52 The one-step reaction of ZnP aryl radicals with the SWNT sidewall is expected to form a special pair mimic ((ZnP–L)2–SWNT (L = p-ph1, m-ph1)). SWNT composed mainly of a semiconducting (13,8)-chirality (produced by an arc-discharge method, average diameter of 1.4 nm) was employed. A ZnP unit with sterically less hindered ethyl groups at the three meso-positions was used to facilitate plausible dimer formation owing to the intense intermolecular π–π interaction between the porphyrin rings. A monomeric porphyrin–SWNT linked system with identical substituents at porphyrin meso-positions (ZnP–p-ph1–SWNT, Fig. 8) was also prepared by the two-step functionalization. Compared to the monomodal Soret band of ZnP–p-ph1–SWNT at 430 nm, the absorption spectrum of (ZnP–p-ph1)2–SWNT in DMF exhibits split Soret bands. Namely, are visible a slightly blue-shifted absorption peak at 427 nm and a red-shifted shoulder at 447 nm, corroborating the formation of the ZnP dimer on SWNT in (ZnP–p-ph1)2–SWNT. However, contrary to the case of pyrene dimer–bridge–SWNTs linked systems that allowed photoinduced CS,50 photoexcitation of the porphyrin dimers and SWNT moieties of (ZnP–p-ph1)2–SWNT results in the selective formation of an exciplex state that directly decayed to the ground state without yielding the complete charge-separated state.52 Although both (Py–ph1)2–SWNT and (ZnP–p-ph1)2–SWNT have the same short phenylene bridge, the electronic coupling between ZnP and SWNT would be larger than that between pyrene and SWNT because the π-system of ZnP is larger than that of pyrene. SWNT with larger diameters (1.4 nm in average) and more defect-free structures revealed by resonant Raman spectroscopies in (ZnP–p-ph1)2–SWNT would also strengthen the electronic coupling than in (Py–ph1)2–SWNT (average diameter; 0.8 nm). The enhanced electronic coupling may be responsible for the exclusive formation of the exciplex state in (ZnP–p-ph1)2–SWNT.Meanwhile, photoexcitation of the porphyrin monomers in ZnP–p-ph1–SWNT also generates the exciplex that directly decays to the ground state. However, the exciplex lifetime of (ZnP–p-ph1)2–SWNT (τ = 24 ps) is 1.5 times longer than that of ZnP–p-ph1–SWNT (τ = 17 ps).52 Considering that (ZnP–p-ph1)2–SWNT and ZnP–p-ph1–SWNT possess the same p-phenylene bridge, their electronic couplings should be comparable and have little impact on the exciplex decay rate constant. Note that the molecular tilt does not occur on SWNT, but occurs on CCG probably on the account of the stronger interaction with 2D CCG than 1D SWNT (vide supra). Despite that the driving force for exciplex decay to the ground state is reduced due to the elevated HOMO levels of the porphyrin dimers, the smaller reorganization energy arising from the porphyrin dimerization may result in the lifetime of the exciplex state in (ZnP–p-ph1)2–SWNT being longer than that in ZnP–p-ph1–SWNT, as observed for CR processes between porphyrin dimers and various acceptors.58 On the other hand, the exciplex lifetime of (ZnP–m-ph1)2–SWNT (Fig. 8), where the dimeric porphyrins are linked to the SWNT sidewall through a m-phenylene linker, is 2 times longer (τ = 49 ps) than that of (ZnP–p-ph1)2–SWNT (τ = 24 ps).52 This may be ascribed to the electronic coupling through the meta-linkage being weaker than that through the para-one, as reported before.116 Such basic information on the effect of donor dimerization on the photodynamics of the exciplex state in D–B–A linked systems is of crucial importance for the design of photoactive devices based on large π-aromatic molecules and nanocarbon materials such as SWNTs.
4. Summary and outlook
Herein, we have reviewed the recent advances in the interpretation of photophysical properties of covalently linked electron-donating molecule–nanocarbon material composites. Systematic studies revealed that the “exciplex state”, an excited-state complex consisting of an π-molecular donor and a nanocarbon acceptor with partial charge-transfer character, plays a pivotal role in determining the photodynamics of these composites, which have been overlooked in some previous reports on D–B–A linked systems. Tuning the electronic coupling of porphyrin–bridge–fullerene systems has an astonishing impact on the quantum yields of the formation of spin-triplet exciplex and charge-separated states.35 Meanwhile, porphyrin-linked SWNTs and graphenes exhibit long-range exclusive formation of their exciplex state, reflecting their 1D and 2D huge π-conjugated structures. The exciplex lifetimes of porphyrin-linked SWNTs are exponentially dependent on the through-bridge edge-to-edge distance, whereas those of porphyrin-linked graphenes are on the direct through-space distance.36,37 That is, SWNTs and graphenes exhibit a marked tendency to form exciplex states that directly decay to the ground state, which increases the difficulty of efficient formation of complete charge-separated states. Despite the charge transport properties of SWNTs and graphenes being superior to those of fullerenes, fullerenes are known to be much better acceptors for high-performance OPV.94,117 Since the formation of complete charge-separated states is prerequisite for high-performance OPVs, the high tendency to form the energy-wasting exciplex state should be one of the critical reasons for the inferior performances of OPV device with SWNTs or graphenes as an electron-acceptor. In addition, graphenes show higher tendency to form the exciplex state than SWNT.50,51 Although the origins of such a difference as well as the real identity of “the exciplex states” are still not clear at the current stage, the π-electron systems spreading around the linked electron-donor units may enhance the electronic coupling between the donor and the acceptor in the order of 0D fullerene, 1D SWNT, and 2D graphene. Future innovative development of spectroscopic and theoretical methods will give us more deep insight into “the exciplex states”. The difference in the photophysical properties of D–B–A linked systems with nanocarbons as acceptor units will be further understood by the investigations on nanocarbon models with well-defined structures and optical and electronic properties, e.g., aceanthrylenes,118,119 carbon nanorings,120–122 and nanographenes.123,124 On the other hand, the pyrene dimerization on SWNTs and graphenes facilitates the formation of complete charge-separated states despite the short length of the phenylene bridge,50,51 whereas the porphyrin dimerization simply results in a significant increase in the exciplex lifetime without forming the complete charge-separated state.52 Overall, our studies show that in donor–bridge–nanocarbon systems appropriate selection of donor and nanocarbon with moderate electronic coupling is essential for the suppression of the exciplex formation and thereby the efficient formation of the complete charge-separated state. The new strategy to tune the ET parameters (i.e., driving force and electronic coupling) by donor dimerization on nanocarbon materials is highly promising for the rational design of photoinduced ET systems. These guidelines are essential for harvesting full potential of carbon-based nanomaterials and developing next-generation optoelectronic and energy devices.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by Grant-in-Aid for Scientific Research (S) (No. JP25220501 to H. I.), Grant-in-Aid for Young Scientists (A) (No. JP26708023 to T. U.), and Grant-in-Aid for Scientific Research on Innovative Areas “New Polymeric Materials Based on Element-Blocks (No. 2401)” (JP15H00737 to T. U.). Authors thank Prof. Akihiko Furube (AIST), Prof. Nikolai V. Tkchenko (Tampere University of Technology), Prof. Yasuhiro Kobori (Kobe University), Prof. Koichi Yamashita (The University of Tokyo) and Prof. Kazu Suenaga (AIST) for the collaborative works in the investigations of structures and photophysical properties of nanocarbon materials.References
- A. J. Hoff and J. Deisenhofer, Phys. Rep., 1997, 287, 1 CrossRef CAS
.
- M. R. Wasielewski, Chem. Rev., 1992, 92, 435 CrossRef CAS
.
- M. D. Ward, Chem. Soc. Rev., 1997, 26, 365 RSC
.
- D. Gust, T. A. Moore and A. L. Moore, Acc. Chem. Res., 2001, 92, 40 CrossRef
.
- J. H. Alstrum-Acevedo, M. K. Brennaman and T. J. Meyer, Inorg. Chem., 2005, 44, 6802 CrossRef CAS PubMed
.
- M. R. Wasielewski, Acc. Chem. Res., 2009, 42, 1910 CrossRef CAS PubMed
.
- T. M. Clarke and J. R. Durrant, Chem. Rev., 2010, 110, 6736 CrossRef CAS PubMed
.
- H. Imahori and Y. Sakata, Adv. Mater., 1997, 9, 537 CrossRef CAS
.
- H. Imahori and Y. Sakata, Eur. J. Org. Chem., 1999, 2445 CrossRef CAS
.
- H. Imahori, Y. Mori and Y. Matano, J. Photochem. Photobiol., C, 2003, 4, 51 CrossRef CAS
.
- H. Imahori, Org. Biomol. Chem., 2004, 2, 1425 CAS
.
- H. Imahori and S. Fukuzmi, Adv. Funct. Mater., 2004, 14, 525 CrossRef CAS
.
- F. D’Souza and O. Ito, Coord. Chem. Rev., 2005, 249, 1410 CrossRef
.
- H. Imahori, Bull. Chem. Soc. Jpn., 2007, 80, 621 CrossRef CAS
.
- H. Imahori, J. Mater. Chem., 2007, 17, 31 RSC
.
- H. Imahori and T. Umeyama, J. Phys. Chem. C, 2009, 113, 9029 CAS
.
- D. M. Guldi, Chem. Commun., 2000, 321 RSC
.
- D. M. Guldi, Chem. Soc. Rev., 2002, 31, 22 RSC
.
- D. M. Guldi, B. M. Illescas, C. M. Atienza, M. Wielopolskia and N. Martín, Chem. Soc. Rev., 2009, 38, 1587 RSC
.
- T. Umeyama and H. Imahori, Energy Environ. Sci., 2008, 1, 120 CAS
.
- T. Umeyama and H. Imahori, J. Phys. Chem. C, 2013, 117, 3195 CAS
.
- S. Fukuzumi and T. Kojima, J. Mater. Chem., 2008, 18, 1427 RSC
.
- R. Chitta and F. D’Souza, J. Mater. Chem., 2008, 18, 1440 RSC
.
- V. Sgobba and D. M. Guldi, Chem. Soc. Rev., 2009, 38, 165 RSC
.
- F. D’Souza, A. S. D. Sandanayaka and T. Ito, J. Phys. Chem. Lett., 2010, 1, 2586 CrossRef
.
- G. Bottari, G. de la Torre, D. M. Guldi and T. Torres, Chem. Rev., 2010, 110, 6768 CrossRef CAS PubMed
.
- F. D’Souza and O. Ito, Chem. Soc. Rev., 2012, 41, 86 RSC
.
- I. V. Lightcap and P. V. Kamat, Acc. Chem. Res., 2013, 46, 2235 CrossRef CAS PubMed
.
- G. A. M. Sáfar, D. C. S. Martins, G. DeFreitas-Silva, J. S. Rebouças, Y. M. Idemori and A. Righi, Synth. Met., 2014, 193, 64 CrossRef
.
- G. Bottari, G. de la Torre and T. Torres, Acc. Chem. Res., 2015, 48, 900 CrossRef CAS PubMed
.
- E. M. Pérez and N. Martín, Chem. Soc. Rev., 2015, 44, 6425 RSC
.
- V. Strauss, A. Roth, M. Sekita and D. M. Guldi, Chem, 2016, 1, 531 CAS
.
- N. Karousis, N. Tagmatarchis and D. Tasis, Chem. Rev., 2010, 110, 5366 CrossRef CAS PubMed
.
- V. Georgakilas, M. Otyepka, A. B. Bourlinos, V. Chandra, N. Kim, K. C. Kemp, P. Hobza, R. Zboril and K. S. Kim, Chem. Rev., 2012, 112, 6156 CrossRef CAS PubMed
.
- T. Higashino, T. Yamada, M. Yamamoto, A. Furube, N. V. Tkachenko, T. Miura, Y. Kobori, R. Jono, K. Yamashita and H. Imahori, Angew. Chem., Int. Ed., 2016, 55, 629 CrossRef CAS PubMed
.
- J. Baek, T. Umeyama, K. Stranius, H. Yamada, N. V. Tkachenko and H. Imahori, J. Phys. Chem. C, 2017, 121, 13952 CAS
.
- T. Umeyama, T. Hanaoka, J. Baek, T. Higashino, F. Abou-Chahine, N. V. Tkachenko and H. Imahori, J. Phys. Chem. C, 2016, 120, 28337 CAS
.
- T. Miura, R. Tao, S. Shibata, T. Umeyama, T. Tachikawa, H. Imahori and Y. Kobori, J. Am. Chem. Soc., 2016, 138, 5879 CrossRef CAS PubMed
.
- N. V. Tkachenko, H. Lemmetyinen, J. Sonoda, K. Ohkubo, T. Sato, H. Imahori and S. Fukuzumi, J. Phys. Chem. A, 2003, 107, 8834 CrossRef CAS
.
- J. Ikemoto, K. Takimiya, Y. Aso, T. Otsubo, M. Fujitsuka and O. Ito, Org. Lett., 2002, 4, 309 CrossRef CAS PubMed
.
- G. de la Torre, F. Giacalone, J. L. Segura, N. Martín and D. M. Guldi, Chem. – Eur. J., 2005, 11, 1267 CrossRef CAS PubMed
.
- F. Oswald, D.-M. S. Islam, Y. Araki, V. Troiani, R. Caballero, P. de la Cruz, O. Ito and F. Langa, Chem. Commun., 2007, 4498 RSC
.
- A. Molina-Ontoria, M. Wielopolski, J. Gebhardt, A. Gouloumis, T. Clark, D. M. Guldi and N. Martín, J. Am. Chem. Soc., 2011, 133, 2370 CrossRef CAS PubMed
.
- M. Wielopolski, A. Molina-Ontoria, C. Schubert, J. T. Margraf, E. Krokos, J. Kirschner, A. Gouloumis, T. Clark, D. M. Guldi and N. Martín, J. Am. Chem. Soc., 2013, 135, 10372 CrossRef CAS PubMed
.
- J. Sukegawa, C. Schubert, X. Zhu, H. Tsuji, D. M. Guldi and E. Nakamura, Nat. Chem., 2014, 6, 899 CrossRef CAS PubMed
.
- F. Oswald, D.-M. S. Islam, M. E. El-Khouly, Y. Araki, R. Caballero, P. de la Cruz, O. Ito and F. Langa, Phys. Chem. Chem. Phys., 2014, 16, 2443 RSC
.
- S. V. Kirner, D. Arteaga, C. Henkel, J. T. Margraf, N. Alegret, K. Ohkubo, B. Insuasty, A. Ortiz and N. Martín, Chem. Sci., 2015, 6, 5994 RSC
.
- O. S. Wenger, Chem. Soc. Rev., 2011, 40, 3538 RSC
.
- M. Taniguchi and J. S. Lindsey, Tetrahedron, 2010, 66, 5549 CrossRef CAS
.
- T. Umeyama, J. Baek, Y. Sato, K. Suenaga, F. Abou-Chahine, N. V. Tkachenko, H. Lemmetyinen and H. Imahori, Nat. Commun., 2015, 6, 7732 CrossRef CAS PubMed
.
- T. Umeyama, J. Baek, J. Mihara, N. V. Tkachenko and H. Imahori, Chem. Commun., 2017, 53, 1025 RSC
.
- J. Baek, T. Umeyama, S. Mizuno, N. V. Tkachenko and H. Imahori, J. Phys. Chem. C DOI:10.1021/acs.jpcc.7b08594
.
- H. Ozeki, A. Nomoto, K. Ogawa, Y. Kobuke, M. Murakami, K. Hosoda, M. Ohtani, S. Nakashima, H. Miyasaka and T. Okada, Chem. – Eur. J., 2004, 10, 6393 CrossRef CAS PubMed
.
- M. Isosomppi, N. V. Tkachenko, A. Efimov and H. Lemmetyinen, J. Phys. Chem. A, 2005, 109, 4881 CrossRef CAS PubMed
.
- A. de la Escosura, M. V. Martínez-Díaz, D. M. Guldi and T. Torres, J. Am. Chem. Soc., 2006, 128, 4112 CrossRef CAS PubMed
.
- F. D’Souza, R. Chitta, S. Gadde, L. M. Rogers, P. A. Karr, M. E. Zandler, A. S. D. Sandanayaka, Y. Araki and O. Ito, Chem. – Eur. J., 2007, 13, 916 CrossRef PubMed
.
- W. Xu, H. Chen, Y. Wang, C. Zhao, X. Li, S. Wang and Y. Weng, ChemPhysChem, 2008, 9, 1409 CrossRef CAS PubMed
.
- A. Takai, C. P. Gros, J.-M. Barbe, R. Guilard and S. Fukuzumi, Chem. – Eur. J., 2009, 15, 3110 CrossRef CAS PubMed
.
- G. Bottari, O. Trukhina, A. Kahnt, M. Frunzi, Y. Murata, A. Rodríguez-Fortea, J. M. Poblet, D. M. Guldi and T. Torres, Angew. Chem., Int. Ed., 2016, 55, 11020 CrossRef CAS PubMed
.
- P. E. Hartnett, C. M. Mauck, M. A. Harris, R. M. Young, Y.-L. Wu, T. J. Marks and M. R. Wasielewski, J. Am. Chem. Soc., 2017, 139, 749 CrossRef CAS PubMed
.
- C. Stangel, A. Charisiadis, G. E. Zervaki, V. Nikolaou, G. Charalambidis, A. Kahnt, G. Rotas, N. Tagmatarchis and A. G. Coutsolelos, J. Phys. Chem. C, 2017, 121, 4850 CAS
.
- J. J. Benson-Smith, J. Wilson, C. Dyer-Smith, K. Mouri, S. Yamaguchi, H. Murata and J. Nelson, J. Phys. Chem. B, 2009, 113, 7794 CrossRef CAS PubMed
.
- A. H. Al-Subi, M. Niemi, N. V. Tkachenko and H. Lemmetyinen, J. Phys. Chem. A, 2012, 116, 9653 CrossRef CAS PubMed
.
- T. J. Kesti, N. V. Tkachenko, V. Vehmanen, H. Yamada, H. Imahori, S. Fukuzumi and H. Lemmetyinen, J. Am. Chem. Soc., 2002, 124, 8067 CrossRef CAS PubMed
.
- M. E. El-Khouly, O. Ito, P. M. Smith and F. D’Souza, J. Photochem. Photobiol., C, 2004, 5, 79 CrossRef CAS
.
- H. Imahori, J. Phys. Chem. C, 2004, 108, 6130 CrossRef CAS PubMed
.
- W. B. Davis, W. A. Svec, M. A. Ratner and M. R. Wasielewski, Nature, 1998, 396, 60 CrossRef CAS
.
- F. Lafolet, S. Welter, Z. Popović and L. D. Cola, J. Mater. Chem., 2005, 15, 2820 RSC
.
- C. Schubert, M. Wielopolski, L.-H. Mewes, G. de Miguel Rojas, C. van der Pol, K. C. Moss, M. R. Bryce, J. E. Moser, T. Clark and D. M. Guldi, Chem. – Eur. J., 2013, 19, 7575 CrossRef CAS PubMed
.
- D. Hanss and O. S. Wenger, Inorg. Chem., 2008, 47, 9081 CrossRef CAS PubMed
.
- D. Hanss and O. S. Wenger, Eur. J. Inorg. Chem., 2009, 3778 CrossRef CAS
.
- C. Luo, D. M. Guldi, H. Imahori, K. Tamaki and Y. Sakata, J. Am. Chem. Soc., 2000, 122, 6535 CrossRef CAS
.
- H. Imahori, K. Tamaki, D. M. Guldi, C. Luo, M. Fujitsuka, O. Ito, Y. Sakata and S. Fukuzumi, J. Am. Chem. Soc., 2001, 123, 2607 CrossRef CAS PubMed
.
- N. V. Tkachenko, H. Lemmetyinen, J. Sonoda, K. Ohkubo, T. Sato, H. Imahori and S. Fukuzumi, J. Phys. Chem. A, 2003, 107, 8834 CrossRef CAS
.
- S. Fukuzumi, H. Imahori, K. Okamoto, H. Yamada, M. Fujitsuka, O. Ito and D. M. Guldi, J. Phys. Chem. A, 2002, 106, 1903 CrossRef CAS
.
-
Electron Transfer from Isolated Molecules to Biomolecules, ed. J. Jortner and M. Bixon, Wiley, New York, 1999 Search PubMed
.
- T. Umeyama, M. Fujita, N. Tezuka, N. Kadota, Y. Matano, K. Yoshida, S. Isoda and H. Imahori, J. Phys. Chem. C, 2007, 111, 11484 CAS
.
- M. Alvaro, P. Atienzar, P. de la Cruz, J. L. Delgado, V. Troiani, H. Garcia, F. Langa, A. Palkar and L. Echegoyen, J. Am. Chem. Soc., 2006, 128, 6626 CrossRef CAS PubMed
.
- T. Arai, S. Nobukuni, A. S. D. Sandanayaka and O. Ito, J. Phys. Chem. C, 2009, 113, 14493 CAS
.
- T. Palacin, H. L. Khanh, B. Jousselme, P. Jegou, A. Filoramo, C. Ehli, D. M. Guldi and S. Campidelli, J. Am. Chem. Soc., 2009, 131, 15394 CrossRef CAS PubMed
.
- T. Umeyama, J. Mihara, H. Hayashi, N. Kadota, V. Chukharev, N. V. Tkachenko, H. Lemmtyinen, K. Yoshida, S. Isoda, M. Takano and H. Imahori, Chem. Commun., 2011, 47, 11781 RSC
.
- Y. Hirana, G. Juhasz, Y. Miyauchi, S. Mouri, K. Matsuda and N. Nakashima, Sci. Rep., 2013, 3, 2959 CrossRef PubMed
.
- N. Karousis, A. S. D. Sandanayaka and T. Hasobe, J. Mater. Chem., 2011, 21, 109 RSC
.
- H.-X. Wang, K.-G. Zhou, Y.-L. Xie, J. Zeng, N.-N. Chai, J. Li and H.-L. Zhang, Chem. Commun., 2011, 47, 5747 RSC
.
- X. Zhang, L. Hou, A. Cnossen, A. C. Coleman, O. Ivashenko, P. Rudolf, B. J. van Wees, W. R. Browne and B. L. Feringa, Chem. – Eur. J., 2011, 17, 8957 CrossRef CAS PubMed
.
- M.-E. Ragoussi, G. Katsukis, A. Roth, J. Malig, G. de la Torre, D. M. Guldi and T. Torres, J. Am. Chem. Soc., 2014, 136, 4593 CrossRef CAS PubMed
.
- T. Umeyama, J. Mihara, N. Tezuka, Y. Matano, K. Stranius, V. Chukharev, N. V. Tkachenko, H. Lemmetyinen, K. Noda, K. Matsushige, T. Shishido, Z. Liu, K. Hirose-Takai, K. Suenaga and H. Imahori, Chem. – Eur. J., 2012, 18, 4250 CrossRef CAS PubMed
.
- S. Park and R. S. Ruoff, Nat. Nanotechnol., 2009, 4, 217 CrossRef CAS PubMed
.
- T. Umeyama, D. Matano, J. Baek, S. Gupta, S. Ito, V. Subramanian and H. Imahori, Chem. Lett., 2015, 44, 1410 CrossRef CAS
.
- S. Niyogi, E. Bekyarova, M. E. Itkis, H. Zhang, K. Shepperd, J. Hicks, M. Sprinkle, C. Berger, C. N. Lau, W. A. de Heer, E. H. Conrad and R. C. Haddon, Nano Lett., 2010, 10, 4061 CrossRef CAS PubMed
.
- G. L. C. Paulus, Q. H. Wang and M. S. Strano, Acc. Chem. Res., 2013, 46, 160 CrossRef CAS PubMed
.
- H. Imahori, S. Kang, H. Hayashi, M. Haruta, H. Kurata, S. Isoda, S. E. Canton, Y. Infahsaeng, A. Kathiravan, T. Pascher, P. Chabera, A. P. Yartsev and V. Sundström, J. Phys. Chem. A, 2011, 115, 3679 CrossRef CAS PubMed
.
- H. Zhou, L. Yang and W. You, Macromolecules, 2012, 45, 607 CrossRef CAS
.
- T. Umeyama and H. Imahori, J. Mater. Chem. A, 2014, 2, 11545 CAS
.
- C. L. Chochos, N. Tagmatarchis and V. G. Gregoriou, RSC Adv., 2013, 3, 7160 RSC
.
- T. Umeyama, T. Miyata, A. C. Jakowetz, S. Shibata, K. Kurotobi, T. Higashino, T. Koganezawa, M. Tsujimoto, S. Gélinas, W. Matsuda, S. Seki, R. H. Friend and H. Imahori, Chem. Sci., 2017, 8, 181 RSC
.
- T. Umeyama, K. Igarashi, D. Sakamaki, S. Seki and H. Imahori, Chem. Commun., 2018, 54, 405 RSC
.
- G. Li, V. Shrotriya, J. Huang, Y. Yao, T. Moriarty, K. Emery and Y. Yang, Nat. Mater., 2005, 4, 864 CrossRef CAS
.
- W. Ma, C. Yang, X. Gong, K. Lee and A. J. Heeger, Adv. Funct. Mater., 2005, 15, 1617 CrossRef CAS
.
- T. Umeyama, S. Shibata, T. Miyata, K. Igarashi, T. Koganezawa and H. Imahori, RSC Adv., 2017, 7, 45697 RSC
.
- P. A. van Hal, J. Knol, B. M. W. Langeveld-Voss, S. C. J. Meskers, J. C. Hummelen and R. A. J. Janssen, J. Phys. Chem. A, 2000, 104, 5974 CrossRef CAS
.
- M. Narutaki, K. Takimiya, T. Otsubo, Y. Harima, H. Zhang, Y. Araki and O. Ito, J. Org. Chem., 2006, 71, 1761 CrossRef CAS PubMed
.
- T. Nakamura, Y. Araki, O. Ito, K. Takimiya and T. Otsubo, J. Phys. Chem. A, 2008, 112, 1125 CrossRef CAS PubMed
.
- N. Banerji, J. Seifter, M. Wang, E. Vauthey, F. Wudl and A. J. Heeger, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 075206 CrossRef
.
- K. Vandewal, S. Albrecht, E. T. Hoke, K. R. Graham, J. Widmer, J. D. Douglas, M. Schubert, W. R. Mateker, J. T. Bloking, G. F. Burkhard, A. Sellinger, J. M. Frechet, J. A. Amassian, M. K. Riede, M. D. McGehee, D. Neher and A. Salleo, Nat. Mater., 2014, 13, 63 CrossRef CAS PubMed
.
- G. L. Closs, M. D. E. Forbes and J. R. Norris, J. Phys. Chem., 1987, 91, 3592 CrossRef CAS
.
- Y. Kobori, S. Sekiguchi, K. Akiyama and S. Tero-Kubota, J. Phys. Chem. A, 1999, 103, 5416 CrossRef CAS
.
- Y. Kobori and T. Miura, J. Phys. Chem. Lett., 2015, 6, 113 CrossRef CAS PubMed
.
- Y. Kobori, R. Noji and S. Tsuganezawa, J. Phys. Chem. C, 2013, 117, 1589 CAS
.
- J. L. Bahr, J. Yang, D. V. Kosynkin, M. J. Bronikowski, R. E. Smalley and J. M. Tour, J. Am. Chem. Soc., 2001, 123, 6536 CrossRef CAS PubMed
.
- M. S. Strano, C. A. Dyke, M. L. Usrey, P. W. Barone, M. J. Allen, H. Shan, C. Kittrell, R. H. Hauge, J. M. Tour and R. E. Smalley, Science, 2003, 301, 1519 CrossRef CAS PubMed
.
- J.-X. Zhao and Y. H. Ding, J. Phys. Chem. C, 2008, 112, 13141 CAS
.
- Y. F. Zhang, C. Suc, Z. F. Liu and J. Q. Li, J. Phys. Chem. B, 2006, 110, 22462 CrossRef CAS PubMed
.
- F. M. Winnik, Chem. Rev., 1993, 93, 587 CrossRef CAS
.
- T. Kawashima, T. Otsubo, Y. Sakata and S. Misumi, Tetrahedron Lett., 1978, 19, 5115 CrossRef
.
- H. Imahori, K. Hagiwara, M. Aoki, T. Akiyama, S. Taniguchi, T. Okada, M. Shirakawa and Y. Sakata, J. Am. Chem. Soc., 1996, 118, 11771 CrossRef CAS
.
- N. Martín, Adv. Energy Mater., 2017, 7, 1601102 CrossRef
.
- H. Dang and M. A. Garcia-Garibay, J. Am. Chem. Soc., 2001, 123, 355 CrossRef CAS PubMed
.
- A. M. Philip, A. R. Mallia and M. Hariharan, J. Phys. Chem. Lett., 2016, 7, 4751 CrossRef CAS PubMed
.
- A. Yagi, Y. Segawa and K. Itami, J. Am. Chem. Soc., 2012, 134, 2962 CrossRef CAS PubMed
.
- K. Miki, T. Matsushita, Y. Inoue, Y. Senda, T. Kowada and K. Ohe, Chem. Commun., 2013, 49, 9092 RSC
.
- D. Lu, G. Zhuang, H. Wu, S. Wang, S. Yang and P. Du, Angew. Chem., Int. Ed., 2017, 56, 158 CrossRef CAS PubMed
.
- D. Kiessling, R. D. Costa, G. Katsukis, J. Malig, F. Lodermeyer, S. Feihl, A. Roth, L. Wibmer, M. Kehrer, M. Volland, P. Wagner, G. G. Wallace, D. L. Officer and D. M. Guldi, Chem. Sci., 2013, 4, 3085 RSC
.
- D. Lungerich, J. F. Hitzenberger, M. Marcia, F. Hampel, T. Drewello and N. Jux, Angew. Chem., Int. Ed., 2014, 53, 12231 CrossRef CAS PubMed
.
| This journal is © The Royal Society of Chemistry 2018 |