Classification of spatially resolved molecular fingerprints for machine learning applications and development of a codebase for their implementation
Abstract
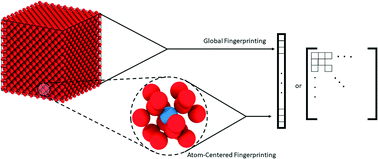
Direct mapping between material structures and properties for various classes of materials is often the ultimate goal of materials researchers. Recent progress in the field of machine learning has created a unique path to develop such mappings based on empirical data. This new opportunity warranted the need for the development of advanced structural representations suitable for use with current machine learning algorithms. A number of such representations termed “molecular fingerprints” or descriptors have been proposed over the years for this purpose. In this paper, we introduce a classification framework to better explain and interpret existing fingerprinting schemes in the literature, with a focus on those with spatial resolution. We then present the implementation of SEING, a new codebase to computing those fingerprints, and we demonstrate its capabilities by building k-nearest neighbor (k-NN) models for force prediction that achieve a generalization accuracy of 0.1 meV Å−1 and an R2 score as high as 0.99 at testing. Our results indicate that simple and generally overlooked k-NN models could be very promising compared to approaches such as neural networks, Gaussian processes, and support vector machines, which are more commonly used for machine learning-based predictions in computational materials science.
- This article is part of the themed collection: Machine Learning and Data Science in Materials Design


 Please wait while we load your content...
Please wait while we load your content...