Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Oral drug suitability parameters†
M. C.
Wenlock

InSilicoLynx Ltd, BioHub at Alderley Park, Mereside, Alderley Park, Cheshire, SK10 4TG, UK. E-mail: mark.wenlock@insilicolynx.com
First published on 5th February 2018
Abstract
Assessing the oral drug suitability of compounds as early as possible within drug discovery is an important objective. This study describes a methodology that attempts to simplify the evaluation of compounds based on their in vivo quantity levels within a mammalian body, represented using a mathematical model that imposes a time limitation on oral absorption and assumes non-instantaneous drug distribution between plasma and tissue. This simplification results in two new oral drug suitability parameters that can quantitatively relate oral dose to in vivo exposure for compounds with vastly different tendencies in terms of absorption into, and elimination from, the body. Consequently, the complexities associated with evaluating a compound's oral drug suitability are simplified to an assessment of these two new parameters. Application of this methodology at the virtual design stage is discussed, along with functionality that accounts for uncertainty related to a compound's distribution kinetics and errors associated to in silico QSAR predictions for the required input data.
Introduction
When assessing the oral drug suitability of compounds it is common to consider physicochemical parameters such as hydrophobicity and molecular size.1,2 Over the past two decades, virtual drug design has been strongly influenced by hypotheses derived from the comparison of large sets of physicochemical property data associated to oral drugs;3–9 in particular, hypotheses that indicate limitations on a compound's predicted log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P. However, such propositions tend to be ambiguous with regard to causality, as they rely heavily on arguments based on simple data trend observations. In practice, a compound's success as an oral drug in humans is predominantly defined by in vivo exposure, efficacy and toxicity factors; the evidence directly implicating a dependence of predicted log
P. However, such propositions tend to be ambiguous with regard to causality, as they rely heavily on arguments based on simple data trend observations. In practice, a compound's success as an oral drug in humans is predominantly defined by in vivo exposure, efficacy and toxicity factors; the evidence directly implicating a dependence of predicted log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P on these in vivo factors is weak and influenced by the type of compounds being considered.8,10
P on these in vivo factors is weak and influenced by the type of compounds being considered.8,10
The octanol–water partitioning system from which a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P is derived, and on which a predicted log
P is derived, and on which a predicted log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P is based, is intended as a model system for compound transfer between aqueous and lipid phases and is arguably too simplistic for a whole mammalian system. This study addresses this point by proposing alternative oral drug suitability parameters for consideration during virtual drug design.
P is based, is intended as a model system for compound transfer between aqueous and lipid phases and is arguably too simplistic for a whole mammalian system. This study addresses this point by proposing alternative oral drug suitability parameters for consideration during virtual drug design.
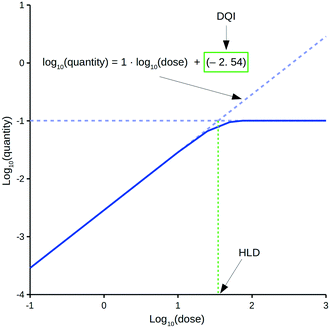
The oral drug suitability parameters are derived from rate equations for determining in vivo quantity levels associated to a relevant mathematical model of a mammalian system. The focus of this study is a mathematical model for a human system in the form of a three-compartment pharmacokinetic (PK) model, which imposes a time limitation on the absorption of an orally dosed drug from the small intestines, assumes non-instantaneous drug distribution between plasma and tissue, and only allows for elimination of the absorbed drug from one compartment.11,12 Application of the proposed PK model in a repeat-dosing simulation can approximate steady-state in vivo data for a quantity (e.g., maximum plasma concentration) as a function of the oral dose, resulting in a dose–quantity curve (Fig. 1).
Each dose–quantity curve has two compound-specific features, which are treated as a pair of oral drug suitability parameters: the first is the dose–quantity intercept (DQI) for the regression line fitted through the curve's linear PK region; the second is the highest dose that still leads to linear PK (or near-linear PK) for the particular quantity (highest linear dose [HLD]). This study describes the methodology for calculating a compound's DQI and HLD, and demonstrates how to interpret the results to assess a compound's oral drug suitability. Importantly, the PK model is not intended to be physiologically accurate, rather it is a minimum model system that permits consideration of key factors related to a drug's in vivo exposure. Hence, the DQI and HLD contain information on the absorption, distribution and elimination properties of a compound based on this model system, which can facilitate the ranking of compounds. However, the calculated DQI and HLD values may differ from an in vivo measurement.
This study considers the application of the aforementioned PK model to 15 known oral drugs. The size of the set was restricted to 15 because of the limited number of compounds (within the literature and the European Bioinformatics Institute's ChEMBL database13) with experimentally derived values for pKa, aqueous solubility at pH 7.4 (and room temperature, solubilitypH7.4), apparent human Caco2 membrane permeability (A to B) at pH 6.5 (Papp,Caco2,pH6.5), human volume of distribution at steady state (Vss), human in vivo plasma clearance (Cl), human in vivo efficacy and, optionally, human plasma protein binding (PPB). However, it is envisaged that the DQI and HLD should be used at the virtual design stage and that such compound information would be generated using in silico QSAR models. Such methods have associated prediction errors, which can be large, so the impact of these errors on the DQI and HLD values is discussed.
Experimental
Compounds and required input data
Table 1 lists the 15 compounds being considered along with the following required input data: pKa, solubilitypH7.4 (M), Papp,Caco2,pH6.5 (cm s−1), Vss (L kg−1), Cl (mL min−1 kg−1) and PPB (% bound). Further details can be found within the ESI.†| Drug | Charge type | pKa | SolubilitypH7.4 (M) | P app,Caco,pH6.5 (cm s−1) | V ss (L kg−1) | Cl (mL min−1 kg−1) | PPB (% bound) |
|---|---|---|---|---|---|---|---|
| Chlorpromazine | Monobase | 9.24 (ref. 14 and 15) | 3.72 × 10−4 (ref. 14, 15, 21 and 22) | 2.00 × 10−5 (ref. 26) | 10.00 (ref. 27) | 16.00 (ref. 29) | 98.64 (ref. 22) |
| Diazepam | Neutral | 1.57 × 10−4 (ref. 22 and 23) | 6.03 × 10−5 (ref. 26) | 1.00 (ref. 27) | 0.38 (ref. 29) | 98.61 (ref. 22) | |
| Diclofenac | Monoacid | 4.26 (ref. 15–18) | 6.53 × 10−3 (ref. 15, 16, 18, 23 and 24) | 5.37 × 10−5 (ref. 26) | 0.19 (ref. 27 and 28) | 3.83 (ref. 28 and 29) | 99.68 (ref. 22) |
| Furosemide | Monoacid | 3.94 (ref. 14, 17 and 19) | 1.78 × 10−1 (ref. 14) | 2.82 × 10−7 (ref. 26) | 0.11 (ref. 27 and 28) | 2.19 (ref. 28 and 29) | 98.37 (ref. 22) |
| Haloperidol | Monobase | 8.63 (ref. 17 and 18) | 7.56 × 10−5 (ref. 18, 21 and 22) | 1.58 × 10−5 (ref. 26) | 17.00 (ref. 27) | 7.80 (ref. 29) | 85.48 (ref. 22) |
| Imipramine | Monobase | 9.50 (ref. 14 and 17) | 9.85 × 10−3 (ref. 14) | 2.75 × 10−5 (ref. 26) | 12.00 (ref. 27) | 13.00 (ref. 29) | 87.87 (ref. 22) |
| Indomethacin | Monoacid | 4.31 (ref. 15, 17 and 20) | 1.44 × 10−3 (ref. 15, 20 and 25) | 2.95 × 10−5 (ref. 26) | 0.16 (ref. 27 and 28) | 1.61 (ref. 28 and 29) | |
| Ketoprofen | Monoacid | 4.25 (ref. 15–17 and 19) | 5.55 × 10−1 (ref. 15 and 16) | 4.68 × 10−5 (ref. 26) | 0.13 (ref. 27) | 1.60 (ref. 29) | 98.73 (ref. 22) |
| Naproxen | Monoacid | 4.23 (ref. 15–19) | 9.87 × 10−2 (ref. 15, 16, 18 and 23) | 4.68 × 10−5 (ref. 26) | 0.09 (ref. 28) | 0.07 (ref. 28) | |
| Nifedipine | Neutral | 5.23 × 10−5 (ref. 18, 21, 22 and 24) | 3.24 × 10−5 (ref. 26) | 0.79 (ref. 27) | 7.30 (ref. 29) | 96.17 (ref. 22) | |
| Phenytoin | Monoacid | 8.06 (ref. 15–18) | 8.51 × 10−5 (ref. 15, 16, 18, 21, 22 and 24) | 3.98 × 10−5 (ref. 26) | 1.40 (ref. 28) | 0.57 (ref. 28) | 87.11 (ref. 22) |
| Pindolol | Monobase | 9.54 (ref. 15) | 2.62 × 10−2 (ref. 15) | 3.89 × 10−5 (ref. 26) | 1.20 (ref. 27) | 7.70 (ref. 29) | |
| Prazosin | Monobase | 6.50 (ref. 17) | 1.48 × 10−5 (ref. 22) | 4.07 × 10−6 (ref. 26) | 0.73 (ref. 27) | 4.70 (ref. 29) | 96.00 (ref. 22) |
| Trimethoprim | Monobase | 7.26 (ref. 17) | 2.17 × 10−3 (ref. 23) | 8.71 × 10−5 (ref. 26) | 1.50 (ref. 27) | 2.10 (ref. 29) | 66.10 (ref. 22) |
| Warfarin | Monoacid | 4.97 (ref. 14, 15, 17 and 18) | 3.35 × 10−3 (ref. 14, 15 and 18) | 4.37 × 10−5 (ref. 26) | 0.12 (ref. 27 and 28) | 0.05 (ref. 28 and 29) | 99.31 (ref. 22) |
PK model
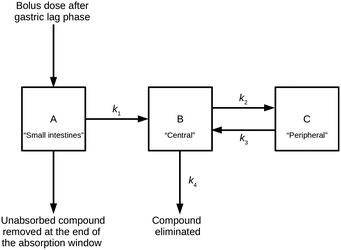
The PK model combines a two-compartment model with an additional compartment to model absorption of extravascular doses of a compound from the small intestines.11,12 This model can be described by a series of linear differential equations that can be solved using the Laplace transformation technique to derive a series of rate equations.30Fig. 2 shows a compartmental representation of the model, and details of the mathematical equations can be found in the ESI.†The application of the rate equations, along with the input data required to calculate compound compartment levels at different time points, constituted a simulation. Simulations were run at a series of doses and included multiple distribution kinetics scenarios. An open-source Python (software) library was written to perform and analyse these simulations.31
To establish steady-state conditions, simulations considered repeat dosing. Using the principle of superposition, compound compartment levels were considered for each repeated dose from time of dose to end of the simulation, and then all levels at each time point were summed for the repeated doses. Compartment A represented a hypothetical uniform cylindrical intestinal segment, filled with a constant intestinal fluid volume (Vintestinal, L) of 0.08 L,32 into which the compound (in solid form) was delivered as a bolus; for this study, the intestinal fluid was represented by aqueous pH 6.5 buffer. The uniform mixing and dissolution process within compartment A was treated as instantaneous and only solubilised compound could undergo the one-way transfer into compartment B; this transfer was treated as either a zero-order or a first-order process, characterised by the absorption rate constant k1 (min−1), similar to the approach used by Dressman et al.12 The model restricted this process to an absorption window, during which compound could only be removed from compartment A by said absorption; any remaining compound at the end of the absorption window was discarded, and the model reverted to a classic two-compartment PK model.33 For clarity, the absorption window represented the transit of this uniform cylindrical slug of intestinal fluid (containing the dosed drug) through the small intestines, during which its shape and volume remained unchanged.
Compartment B (the central compartment) represented the body spaces into which a compound could distribute extremely rapidly (i.e., plasma and well-perfused tissues, including the major eliminating organs). The volume of compartment B was compound specific and represented the compound's initial dilution volume (Vcentral, L). Compartment C (the peripheral compartment) represented the body spaces into which a compound distributed more slowly. Compound transfer from compartment B to compartment C was treated as a first-order process, characterised by the rate constant k2 (min−1), and the reverse process was characterised by the rate constant k3 (min−1). It was assumed that, once absorbed, compound could only be removed permanently from the body from compartment B via a first-order process, characterised by the rate constant k4 (min−1).
Simulation time frame
Each simulation spanned 168 h and comprised 14 repeat doses of similar size for each compound. Each simulation time frame consisted of a start time (t0, min) and an end time (tend, min). With respect to the ith dose, ti (min) was the time that this dose was given, and the first dose (t1) was equal to t0. The time of subsequent doses (t2, t3, etc.) was 12 h after the previous dose and reflects the dosing interval. Mathematically, each dose was considered in isolation, where the amounts of compound in the PK model's three compartments was zero at ti. A bolus of the ith dose appeared in compartment A at time ti,A, where the time difference between ti and ti,A represented an absorption delay of 1 h to reflect the gastric lag phase.34 The absorption window started at ti,A and ended at time ti,B, and equated to 4 h.35,36 Compound in compartment B was transferred to compartment C or removed from further consideration during the time between ti,A and tend. This time period also reflected the time during which compound in compartment C could be transferred to compartment B.Saturation state of compartment A
For scenarios where Vintestinal was saturated with compound at ti,A, a constant rate of compound transferred from compartment A to compartment B applied, given by k1 multiplied by the saturated amount of compound in the intestinal fluid (mg). The latter was derived from the compound's aqueous solubility at pH 6.5 (solubilitypH6.5, M) multiplied by its molecular weight and VIntestinal. This rate of transfer was considered up to time ti,B or ti,A,unsaturated, when Vintestinal became unsaturated. At ti,A,unsaturated the amount of compound remaining in compartment A reflected its solubilitypH6.5, from which point the rate of transfer followed first-order kinetics until time ti,B.The solubilitypH6.5 was calculated by multiplying a compound's solubilitypH7.4 by the ratio of its fraction neutral at pH 7.4 to its fraction neutral at pH 6.5; the fraction neutral values were calculated using the method described by Wenlock.37
Simulation time points
Each simulation was defined by approximately 1000 time points. This included time points at 15 min intervals between t0 and tend, along with 336 randomly selected time points from the same time frame. The following specific time points were also considered: t0, ti, ti,A, ti,B, tend and, where applicable, ti,A,unsaturated.Estimating k1
Estimations were based on a compound's predicted human jejunal effective permeability at pH 6.5 (Peff,human,pH6.5, cm s−1) from a uniform cylindrical intestinal segment, filled with intestinal fluid equal to Vintestinal, using the following equation:| k1 = (SA·Peff,human,pH6.5·60)/Vintestinal | (1) |
P eff,human,pH6.5 was estimated based on a compound's Papp,Caco2,pH6.5 using a similar approach to that previously described.37,41 Critically, this approach focuses on the establishment of a (log10–log10) linear regression equation for a set of compounds between their neutral species human membrane permeability at pH 6.5 (Pm,human,neutral,pH6.5, cm s−1) and their neutral species human Caco2 membrane permeability (A to B) at pH 6.5 (Pm,Caco2,neutral,pH6.5, cm s−1). For this study, a larger set of 32 compounds was used to establish the following regression equation:
| log10(Pm,human,neutral,pH6.5) = 0.916·log10(Pm,Caco2,neutral,pH6.5) + 1.579 | (2) |
Fraction escaping first-pass metabolism (Fh)
The model assumes that drug absorption is exclusively through the small intestines, with no gut wall metabolism, and that Fh can be estimated using the equation:42| Fh = 1 − Clb/Qh | (3) |
Distribution kinetics scenarios and estimates for k2, k3 and k4
Three volume of distribution terms are relevant for each compound considered: Vcentral, Vss and the terminal volume of distribution (Vterminal, L). A compound's Vss value is one of the model's required input data values (see Table 1). With respect to Vcentral and Vterminal, each simulation considers five distribution scenarios: (i) Vcentral equals 3.0 L, and the ratio of Vterminal to Vss equals 1.1; (ii) Vcentral equals 50% of the Vss, and the ratio of Vterminal to Vss equals 1.1; (iii) Vcentral equals 3.0 L, and the ratio of Vterminal to Vss equals 2.0; (iv) Vcentral equals 50% of the Vss, and the ratio of Vterminal to Vss equals 2.0; and (v) Vcentral equals the mid-point between the two previous values of Vcentral, and Vterminal equals the mid-point between the two previous values of Vterminal. The first four scenarios represent possible extreme values and the fifth represents a mid-point value for a compound.For each scenarios, values for k2, k3 and k4 were derived using the values for Vcentral, Vss, Vterminal and Cl, in conjunction with rearrangement of standard mathematical equations associated to a two-compartment model.33 Details of these equations can be found in the ESI.†
Five simulations were performed for each compound and each dose, based on the five scenarios.
Doses considered
Simulations were run at 20 different oral doses (mg): 0.000001, 0.000005, 0.00001, 0.00005, 0.0001, 0.001, 0.01, 0.1, 1, 10, 25, 50, 75, 100, 250, 500, 1000, 2500, 5000, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000.
000.
Quantities calculated
A simulation resulted in estimates of quantities of drug in compartments B and C at different time points. For each dose, the compound levels at steady state in compartment B were calculated, including the maximum concentration (Css,central,max, mg L−1) and area under the curve (AUCss,central, mg min L−1). Steady-state conditions were assumed to have been reached by the time of the last repeat dose in a simulation. The AUCss,central was calculated using the composite Simpson's rule, integrating over the time course of the last repeat dose. Free levels were calculated by multiplying the total Css,central,max or AUCss,central by the fraction unbound (i.e., (100 − % bound)/100).The quantities calculated for each simulation were collated and used to create a (log10–log10) dose–quantity curve for each distribution kinetics scenario.
Estimating DQI and HLD
For a set of dose–quantity data, the DQI equals the intercept for a linear regression equation through the region of the log10(dose) versus the log10(quantity) curve, where the slope was approximately equal to 1 (within ±0.0001). The HLD was the log10(dose) calculated using said linear regression equation and the maximum value of the log10(quantity) data (i.e., log10(max_quantity)). Typically, this maximum value reflected the level of the horizontal plateau (Fig. 1). In the few cases where no plateau was observed, the maximum value was that of the highest dose considered.Assessing the impact of errors on DQI and HLD
Variations in DQI and HLD values associated to total level quantities, based on errors in Vss and Cl values for each compound, were also considered. An additional 50 scenarios were calculated for each compound, where original values for these two parameters were replaced by values randomly selected from a Gaussian distribution. Each distribution was based on the log10(original value) and a standard deviation value of 0.3.Presentation of DQI and HLD data
Each set of DQI and HLD data was treated as a Cartesian coordinate pair; due to the five distribution kinetics scenarios, each compound had five pairs. Where errors were considered, each compound had 255 coordinate pairs (i.e., five distribution kinetics scenarios for each of the 51 input data scenarios). Non-self-intersecting closed polygons, whose vertices were described using these Cartesian coordinates in the DQI–HLD plane, were used to represent each compound. The centroid and area of each polygon were calculated using standard methods. Again using standard methods, the second moments of area of each polygon were calculated to reflect the distribution of vertices in the x-axis (i.e., HLD dimension) and y-axis (i.e., DQI dimension).Results and discussion
DQI and HLD parameters
The proposed oral drug suitability parameters are intended to provide insight into the in vivo quantities of a compound based on a relevant PK model of a mammalian system. For the purpose of this study, steady-state conditions are of interest, and 14 repeat doses within a simulation are considered sufficient to establish such. Importantly, the DQI and HLD parameters are composite terms that simplify the understanding of how a compound with a given pKa, solubilitypH7.4, Papp,Caco2,pH6.5, Vss, Cl and (in the case of free levels) PPB profile behaves within the PK model, facilitating dose predictions.Fig. 1 highlights a typical dose–quantity curve resulting from the application of the PK model. It is characterised by a linear region with a slope of 1 for doses below a certain limit. As the dose increases above this limit, compartment A becomes increasingly saturated for the duration of the absorption window. This results in the dose–quantity curve bending as the dose increases, eventually plateauing. For the linear region, the corresponding regression equation takes the form of:
| log10(quantity) = 1·log10(dose) + DQI | (4) |
Rearrangement of eqn (4) leads to eqn (5) or (6):
| quantity = dose·10DQI | (5) |
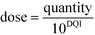 | (6) |
However, these equations only apply up to a log10(dose) equal to the HLD; this equates to the extrapolated log10(dose), using eqn (4), for the log10(max_quantity) observed for a particular distribution kinetics scenario (Fig. 1). The HLD value arrived at using this method is not strictly the HLD, as the dose–quantity curve has already begun to deviate from linearity at this log10(dose) (Fig. 1); rather, it is an approximation using a standardised approach.
Importantly, the DQI and HLD provide a simple way to understand a compound's dose–quantity curve. A plot of DQI against HLD provides an alternative scale against which to evaluate different compounds.
PK model
The PK model used in this study is considered the minimum necessary to account for time-limited oral absorption, non-instantaneous drug distribution between plasma and tissue, and elimination from the central compartment (B). The PK model is intended to be a generic model for use at the virtual drug design stage, and the model settings described in the Experimental section are intended to have broad applicability. Importantly, the PK model and the associated constraints may not be optimal for all compounds. The approach used for modelling oral absorption is based on that used by Dressman et al.12 It is simplistic in nature but deemed sufficient for use at the virtual drug design stage. More complex models are available and Sjögren et al. can provide further insight.41 For clarity, the absorption window is necessary to account for non-linear PK resulting from compound absorption limitations, and the calculation of a compound's HLD is dependent on this feature.Other PK models based on this linear differential equation approach are possible – rate equations for some alternative PK models can be found in the ESI.† The simplest of these is a one-compartment intravenous (bolus dosing) model that only considers a first-order rate constant for elimination.43 This model can be extended to include an oral absorption step – the approached used by Wenlock and Page.37,42 Such a model is applicable for compounds where oral absorption cannot be assumed to be instantaneous; it can also be refined to account for time-limited oral absorption, and details of this can be found in the ESI.† A limitation of one-compartment models is the assumption of instantaneous drug distribution between plasma and tissue; this is overcome in the present PK model by use of a second compartment that permits distribution kinetics to be modelled. For reference, details of a two-compartment intravenous model can be found in the ESI.†
Distribution kinetics scenarios
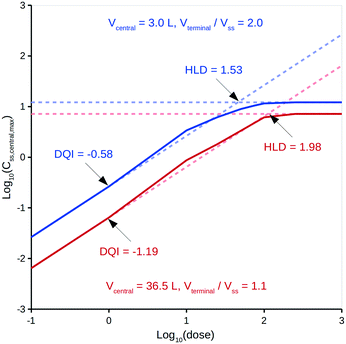
Treating distribution of absorbed drug as not being instantaneous can lead to significant variations in calculated in vivo quantities.33 Specifically, the model assumes non-instantaneous distribution between compartments B and C, albeit distribution within each compartment is instantaneous.It is intended that DQI and HLD be calculated at the virtual drug design stage using in silico technologies37,44 to provide the input data, but, for simplicity, this study only considers experimentally derived input data. With respect to a compound's distribution kinetics, it is unlikely that there will be any insight into these at the virtual design stage. To account for this, the model considers five hypothetical distribution kinetics scenarios for each compound, intended to cover a range of possibilities that encompass the true situation. These scenarios depend on a range of hypothetical values for a compound's Vcentral and Vterminal. Vcentral ranges from 3.0 L, which is the approximate value for the plasma volume in human, to a value that is 50% of the compound's Vss; a mid-point value is also considered. Vterminal ranges from 1.1 times the Vss to 2.0 times the Vss; a mid-point value is also considered. For comparison, Rowland and Tozer33 provide human details for aspirin, salicylic acid and gentamicin C: their Vcentral values can be calculated as 5.3, 6.8 and 14.0 L, respectively, and their Vterminal values as 1.1-, 1.3- and 5.1-fold greater than Vss, respectively. The Vterminal of gentamicin C is considered an extreme and a value 2.0-fold greater than Vss deemed appropriate. To illustrate the effect of these different distribution kinetics scenarios, Fig. 3 shows the dose versus Css,central,max curves generated by the PK model for two of these scenarios for diazepam (further details can be found in the ESI†).
It can be seen from Fig. 3 that differing distribution kinetics scenarios can lead to significant variation in values for DQI (i.e., 2.1-fold) and HLD (i.e., 1.3-fold).
Visualising DQI and HLD data
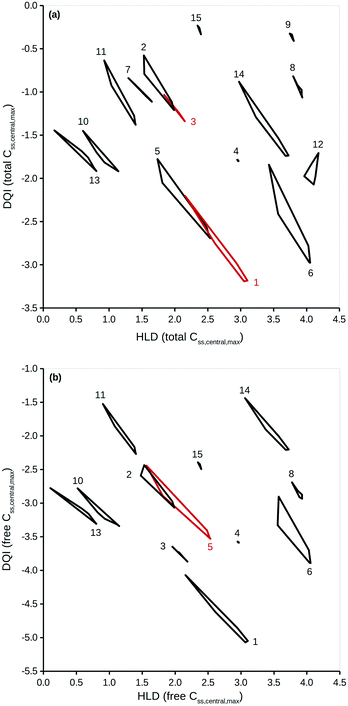
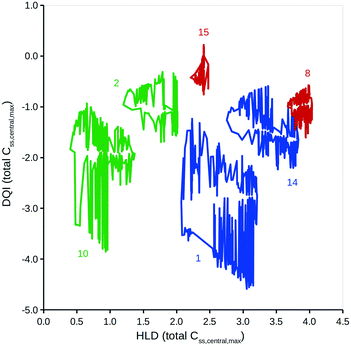
To properly reflect the lack of knowledge regarding a compound's distribution kinetics at the virtual design stage it is important to consider the DQI and HLD from each of the five distribution kinetics scenarios. A way of visualising this information is to treat each pair of DQI and HLD values as a Cartesian coordinate within the DQI–HLD plane, to represent a vertex of a non-self-intersecting closed polygon. Fig. 4 shows such a plot for the Css,central,max total levels for the 15 compounds considered, and a similar plot for the Css,central,max free levels (further details can be found in the ESI†).The polygons shown in Fig. 4 highlight the DQI–HLD space occupied by a compound. The extent of the area overlap of the polygons for two different compounds reflects their similarity. Importantly, at the virtual design stage it is not possible to define precise values for a compound's DQI and HLD. Instead, it is possible to determine an area of DQI–HLD space, defined by a non-self-intersecting closed polygon, where the true value lies. Provided that the two polygons do not overlap, the compounds can be argued to have distinct DQI and HLD values.
This method can be expanded to incorporate errors in the estimation of the input data. A Gaussian distribution can be assumed, based on the original value and an estimation of the associated standard deviation. Additional simulations using randomly selected values from such a Gaussian distribution can then be considered. To illustrate, DQI and HLD were calculated for the 15 compounds, using 50 additional simulations to account for an error of 0.3 on a logarithmic base 10 scale for the values of Vss and Cl. To simplify the plot in Fig. 5, DQI–HLD polygons are shown for only six compounds: chlorpromazine (monobase), diazepam (neutral), ketoprofen (monoacid), nifedipine (neutral), trimethoprim (monobase) and warfarin (monoacid) (further details can be found in the ESI†). It is clear from Fig. 5 that the polygons are very irregular, but again, provided that two polygons do not overlap, the compounds can be argued to have distinct DQI and HLD values. This approach also applies when the input data are sourced from in silico QSAR models, where any prediction error is expressed as a standard deviation.45
The areas covered by the different polygons vary, with that for chlorpromazine being the largest and that for warfarin the smallest. The calculated areas are summarised in Table 2, along with the polygons' second moment of area and centroid values in the DQI and HLD dimensions. The second moment of area indicates the sensitivity of the compound to errors in the input data with respect to the DQI and HLD dimensions; the larger the value, the greater the sensitivity. With respect to warfarin, the DQI value is more sensitive to the combined errors in the values of Vss and Cl than that for HLD; the reverse is true for prazosin. It is useful to think of the HLD dimension reflecting the ability of a compound to be absorbed into the body, while the DQI dimension reflects the extent of elimination of a compound from the body.
| Drug | Area | Second moment of area | Centroid | ||
|---|---|---|---|---|---|
| HLD | DQI | HLD | DQI | ||
| Chlorpromazine | 1.72 | 15.30 | 11.88 | 2.61 | −2.93 |
| Diazepam | 0.33 | 0.31 | 0.89 | 1.63 | −0.94 |
| Diclofenac | 0.73 | 1.82 | 3.04 | 2.03 | −1.56 |
| Furosemide | 0.09 | 0.36 | 0.74 | 2.93 | −2.03 |
| Haloperidol | 1.58 | 13.27 | 5.88 | 1.90 | −2.83 |
| Imipramine | 1.00 | 9.68 | 13.96 | 3.74 | −3.06 |
| Indomethacin | 0.20 | 0.21 | 0.47 | 1.52 | −1.02 |
| Ketoprofen | 0.11 | 0.11 | 1.63 | 3.88 | −1.00 |
| Naproxen | 0.05 | 0.01 | 0.70 | 3.72 | −0.45 |
| Nifedipine | 0.78 | 3.54 | 0.51 | 0.77 | −2.07 |
| Phenytoin | 0.46 | 0.62 | 0.60 | 1.11 | −1.13 |
| Pindolol | 0.33 | 1.32 | 5.18 | 3.98 | −1.95 |
| Prazosin | 0.80 | 4.35 | 0.17 | 0.39 | −2.30 |
| Trimethoprim | 0.49 | 0.99 | 5.28 | 3.26 | −1.39 |
| Warfarin | 0.05 | 0.01 | 0.29 | 2.38 | −0.30 |
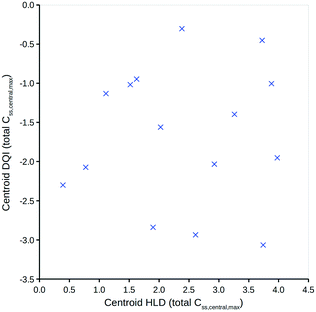
To simplify the information represented by the polygons in Fig. 5, it is proposed that the centroid coordinate could be used to standardise comparisons. Fig. 6 shows a DQI–HLD plot for the total level Css,central,max centroid values for the 15 compounds considered.
Interpreting the DQI and HLD oral drug suitability parameters
Fig. 6 shows how different compounds have vastly different tendencies in terms of absorption and elimination. Absorption is indicated by a compound's centroid value on the HLD dimension, and elimination by a compound's centroid value on the DQI dimension. Arguably, compounds with a higher DQI (i.e., lower elimination) are preferable, but a higher HLD can compensate for a lower DQI. Consider the two monobases prazosin and chlorpromazine: prazosin has a higher centroid DQI (total Css,central,max) of −2.30, compared with −2.93 for chlorpromazine, but a lower centroid HLD (total Css,central,max) of 0.39 compared with 2.61 for chlorpromazine. If the HLD value is used as the log10(dose) in eqn (4), as shown in eqn (7) (where the slope of 1 is omitted):| log10(max_quantity) = HLD + DQI | (7) |
These observations are well established, but evaluation of the properties of oral compounds (i.e., pKa, solubilitypH7.4, Papp,Caco2,pH6.5, Vss, Cl and, optionally, PPB) can be vastly simplified to a quantitative comparison within the two dimensions of DQI and HLD. The magnitude of a compound's DQI and HDI should be considered in conjunction with the desired log10(quantity).
Proposed use of DQI and HLD within virtual drug design
It is envisaged that input data for the present PK model would be sourced from in silico QSAR models.37,44 At the virtual design stage many potential compounds can be considered and it is proposed that their DQI–HLD polygon areas be calculated as described (including consideration of errors in the estimations of the input data).45 The results of these calculations can be visualised as described to give insight into the polygon DQI–HLD space occupied by different compounds. These compounds can also be ranked by application of eqn (5) or (7). For a target log10(max_quantity) requirement, eqn (7) can be used to estimate the log10(max_quantity) for each compound; if this exceeds what is needed, a lower log10(dose) will suffice. However, if the calculated log10(max_quantity) is less than what is needed, then such compounds are not viable as absorption limitations would prevent the use of a higher dose. Similarly, if compounds need to be ranked on the magnitude of a quantity at a particular dose, e.g., 50 mg, eqn (5) could be applied using a value of 50 mg for compounds with an HLD ≥1.70 (i.e., log10(50)) and an anti-log10(HLD) value for those compounds with an HLD <1.70.DQI and in vivo efficacy
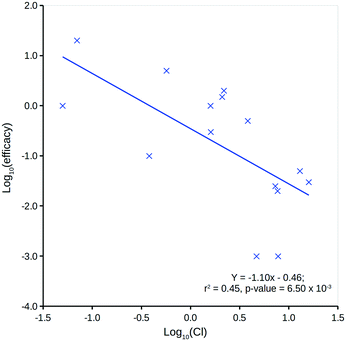
The DQI is a single factor that relates dose to a compound's in vivo (steady-state) quantity following repeat oral dosing in a model system representation of the body. It can be considered a measure of a compound's in vivo exposure.Human in vivo efficacy (mg L−1) data for the 15 compounds considered have been sourced from Schulz et al. (further details can be found in the ESI†).46 Comparison to predicted log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P (ref. 13) indicates a very weak, non-significant linear relationship, but comparison to Cl shows a significant linear relationship (Fig. 7). This is not unexpected, as a compound's Cl will heavily influence in vivo levels – with respect to an intravenous one-compartment model, the steady-state concentration upon repeat dosing is, in theory, inversely proportional to Cl.43
P (ref. 13) indicates a very weak, non-significant linear relationship, but comparison to Cl shows a significant linear relationship (Fig. 7). This is not unexpected, as a compound's Cl will heavily influence in vivo levels – with respect to an intravenous one-compartment model, the steady-state concentration upon repeat dosing is, in theory, inversely proportional to Cl.43
Fig. 8 shows two plots between the 15 compounds' human in vivo efficacy and their centroid DQI for (a) total level Css,central,max and (b) total level AUCss,central quantities (further details can be found in the ESI†). Both show significant linear relationships, such that those that displaying human in vivo efficacy at higher levels tend to have higher centroid DQI and vice versa. The statistics for both plots are slightly better than for the plot in Fig. 7. It can be argued that these centroid DQI values contain slightly more information than Cl for this small data set of 15 compounds. This can be understood from the perspective that oral absorption and drug distribution will have influence over in vivo levels in addition to that of Cl. It can be inferred from these plots that compounds with lower potency require a higher centroid DQI (total level Css,central,max or AUCss,central). This can be understood from the perspective of a fixed dose, such that a less potent compound requires more of the oral dose to be in the central compartment at steady state to drive the therapeutic effect, whereas a more potent compound requires less of the oral dose to be in the central compartment to drive a similar effect.
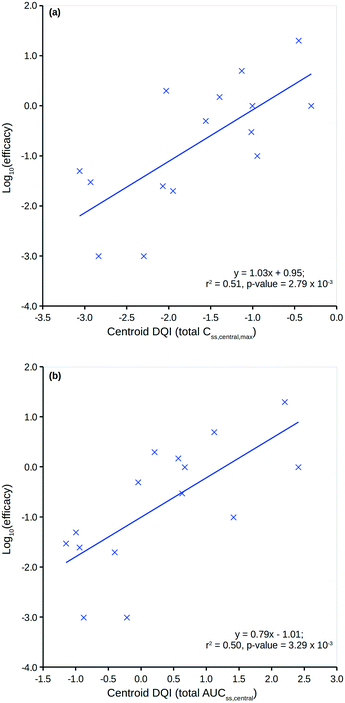 | ||
| Fig. 8 Human in vivo log10(efficacy) versus the total level centroid DQI for (a) Css,central,max and (b) AUCss,central. | ||
Clearly, an appreciation of potency is a key factor in understanding the plots in Fig. 8. Still, the centroid DQI values for the total level Css,central,max or AUCss,central quantities are sufficient to explain approximately half of the information in the human in vivo efficacy values for the 15 compounds.
Relatedly, DQI and HLD values can be proposed as novel compound descriptors for use in conjunction with QSAR modelling methods (and other descriptors) to model other in vivo quantity endpoints. At the virtual design stage, such an approach would involve use of in silico predictions for input data for the model to derive DQI and HLD values, which could then be used as descriptors in further in silico models.
Additional considerations
This study uses solubility7.4 data generated at room temperature, when 37 °C would be more relevant. It is reasonable to assume that solubility7.4 will increase with temperature in all cases, resulting in higher HLD values. Furthermore, variations in the magnitude of model parameters (e.g., Vintestinal, Vcentral, Vterminal to Vss ratio, absorption window, dosing intervals, etc.) will lead to variations in DQI and HLD values. However, the approach discussed here focuses on the evaluation of DQI and HLD for a set of compounds within a standardised PK model (with specific settings) and it is the relative, rather than absolute, values that matter. If absolute values are important, then correction factors are required. For example, if the in vivo quantity and corresponding dose for a representative set of compounds are known, DQI values could be determined using the method described in this work and eqn (6) applied to predict the doses based on the known in vivo quantity. Correction factors for the predicted dose can be derived from a linear regression equation between the known and predicted doses. A similar approach can be used to determine correction factors for an in vivo quantity.Although this study focuses on determining DQI and HLD for the total and free level Css,central,max and AUCss,central, other in vivo quantities could also be assessed using this model. These include total and free levels for the average concentration (Css,central,average) and the minimum concentration (Css,central,min) at steady state in compartment B. In addition, the corresponding levels in compartment C (peripheral compartment) can be considered, including steady-state total and free levels for the maximum concentration (Css,peripheral,max), the average concentration (Css,peripheral,average), the minimum concentration (Css,peripheral,min) and the area under the curve AUCss,peripheral.
Importantly, a twice-daily dosing scenario is considered; changing the dosing interval will lead to different DQI and HLD values for the same compound. Changing the simulation length can also affect these values, in particular if it is shortened. From a virtual drug design perspective, consideration of 14 repeat doses using a once- or twice-daily dosing scenario is recommended.
With respect to the use of 20 different dose simulations to define a dose–quantity curve, this can be reduced to two in theory. The DQI can be determined from a simulation using a very low dose (e.g., 0.000001 mg), where linear PK can be assumed. The HLD can be determined from a simulation using a very high dose (e.g., 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000.0 mg), where compartment A can be assumed to be saturated throughout the absorption window and the corresponding log10(quantity) is at its maximum (i.e., log10(max_quantity)). Relatedly, the standardised method used to determine the HLD only provides an approximation – other methods can be used, including fitting the dose–quantity curve to a power function of the form:
000.0 mg), where compartment A can be assumed to be saturated throughout the absorption window and the corresponding log10(quantity) is at its maximum (i.e., log10(max_quantity)). Relatedly, the standardised method used to determine the HLD only provides an approximation – other methods can be used, including fitting the dose–quantity curve to a power function of the form:
| log10(quantity) = log10(max_quantity) − log10(1 + 10HLD−log10(dose)) | (8) |
The application of eqn (8) using a least-fit method benefits from the use of as many data points as possible to define the transition region of the dose–quantity curve from linear to non-linear PK.
The DQI and HLD calculations can be made in different mammalian species by adjusting the PK model settings accordingly and by using species-specific in silico predictions for Vss, Cl and PPB (and assuming the use of Papp,Caco2,pH6.5 for other species).
Finally, an extension of this study, which is beyond the scope of the present work due to its size and complexity, would be to use in silico QSAR models for pKa, solubilitypH7.4, Papp,Caco2,pH6.5, Vss, Cl and (optionally) PPB to predict the input data for a larger set of compounds, calculate their DQI values, and assess how well they relate to in vivo efficacy and toxicity data.
Conclusions
Assessing the oral drug suitability of compounds at the virtual design stage is an important objective. This study describes a methodology that provides an alternative to the heuristic approaches that emphasise controlling a compound's physicochemical properties. The methodology attempts to simplify the evaluation of compounds based on their estimated in vivo quantity levels within a mammalian body. This simplification comes from the application of the compound-specific DQI and HLD values for a particular in vivo quantity, calculated by assessing a series of PK model simulations. In essence, the PK model takes the form a series of rate equations that can estimate the varying exposure of a compound in different parts of the body over time and repeated oral dosing; for this study, the focus was on steady-state exposure levels. An open-source Python library31 provides a mechanism to perform such complex calculations, also taking into consideration distribution kinetics variations and random (Gaussian) error in the values of the input data. Such functionality facilitates the use of this method at the virtual design stage, where in silico QSAR models can be used to provide the input data and the associated prediction errors factored into the calculation of a compound's DQI and HLD. The DQI parameter is a power term that relates an oral dose of a compound to its estimated in vivo quantities; for a given dose, a larger DQI value corresponds to a larger in vivo quantity. This is only relevant during linear PK conditions and the corresponding HLD value approximates the upper dose limit of applicability.Application of this methodology to 15 known oral drugs demonstrates how different compounds that have vastly different tendencies in terms of absorption into, and elimination from, the body can be compared on the same scale. In spite of the computational complexities associated with gaining such insight, DQI and HLD provide a direct relationship between a compound's dose and in vivo exposure. Evaluation of a compound's oral drug suitability is simply dependent on the ability to match a compound's dose to the required in vivo exposure.
Conflicts of interest
In carrying out this work, the author has used computational tools supplied by InSilicoLynx Ltd, of which he is the sole company share owner. InSilicoLynx Ltd is a member of the RSC Enterprise Plus program.Acknowledgements
The author thanks Lindsay North for her assistance in copy-editing the manuscript.Notes and references
- A. Leo, C. Hansch and D. Elkins, Chem. Rev., 1971, 71, 525 CrossRef CAS.
- C. Pidgeon, S. Ong, H. Liu, X. Qiu, M. Pidgeon, A. H. Dantzig, J. Munroe, W. J. Hornback, J. S. Kasher, L. Glunz and T. Szczerba, J. Med. Chem., 1995, 38, 590 CrossRef CAS PubMed.
- C. A. Lipinski, F. Lombardo, B. W. Dominy and P. J. Feeny, Adv. Drug Delivery Rev., 1997, 23, 3 CrossRef CAS.
- T. Sakaeda, N. Okamura, S. Nagata, T. Yagami, M. Horinouchi, K. Okumura, F. Yamashita and M. Hashida, Biol. Pharm. Bull., 2001, 24, 935 CAS.
- M. C. Wenlock, R. P. Austin, P. Barton, A. M. Davis and P. D. Leeson, J. Med. Chem., 2003, 46, 1250 CrossRef CAS PubMed.
- P. D. Leeson and A. M. Davis, J. Med. Chem., 2004, 47, 6338 CrossRef CAS PubMed.
- P. D. Leeson and B. Springthorpe, Nat. Rev. Drug Discovery, 2007, 6, 881 CrossRef CAS PubMed.
- J. D. Hughes, J. Blagg, D. A. Price, S. Bailey, G. A. DeCrescenzo, R. V. Devraj, E. Ellsworth, Y. M. Fobian, M. E. Gibbs, R. W. Gilles, N. Greene, E. Huang, T. Krieger-Burke, J. Loesel, T. Wager, L. Whiteley and Y. Zhang, Bioorg. Med. Chem. Lett., 2008, 18, 4872 CrossRef CAS PubMed.
- M. P. Gleeson, J. Med. Chem., 2008, 51, 817 CrossRef CAS PubMed.
- M. C. Wenlock, Med. Chem. Commun., 2017, 8, 571 RSC.
- L. Z. Benet, J. Pharm. Sci., 1972, 61, 536 CrossRef CAS PubMed.
- J. B. Dressman, D. Fleisher and G. L. Amidon, J. Pharm. Sci., 1984, 73, 1274 CrossRef CAS PubMed.
- A. P. Bento, A. Gaulton, A. Hersey, L. J. Bellis, J. Chambers, M. Davies, F. A. Krüger, Y. Light, L. Mak, S. McGlinchey, M. Nowotka, G. Papadatos, R. Santos and J. P. Overington, Nucleic Acids Res., 2014, 42, D1083 CrossRef CAS PubMed European Bioinformatics Institute's ChEMBL database (version 20), https://www.ebi.ac.uk/chembl. Data made available under a Creative Commons Attribution-Share Alike 3.0 Unported (CC BY-SA 3.0) license (http://creativecommons.org/licenses/by-sa/3.0/).
- K. J. Box, G. Völgyi, E. Baka, M. Stuart, K. Takács-Novák and J. E. A. Comer, J. Pharm. Sci., 2006, 95, 1298 CrossRef CAS PubMed.
- B. Bard, S. Martel and P. A. Carrupt, Eur. J. Pharm. Sci., 2008, 33, 230 CrossRef CAS PubMed.
- A. Avdeef, Adv. Drug Delivery Rev., 2007, 59, 568 CrossRef CAS PubMed.
- X. Sui, J. Sun, H. Li, Y. Wang, J. Liu, X. Liu, W. Zhang, L. Chen and Z. He, Eur. J. Med. Chem., 2009, 44, 4455 CrossRef CAS PubMed.
- M. C. Wenlock, R. P. Austin, T. Potter and P. Barton, J. Lab. Autom., 2011, 16, 276 CrossRef PubMed.
- A. Avdeef and K. Y. Tam, J. Med. Chem., 2010, 53, 3566 CrossRef CAS PubMed.
- C. A. S. Bergström, C. M. Wassvik, K. Johansson and I. Hubatsch, J. Med. Chem., 2007, 50, 5858 CrossRef PubMed.
- Y. W. Alelyunas, R. Liu, L. Pelosi-Kilby and C. Shen, Eur. J. Pharm. Sci., 2009, 37, 172 CrossRef CAS PubMed.
- ChEMBL document id: CHEMBL3301361.
- D. S. Palmer, A. Llinàs, I. Morao, G. M. Day, J. M. Goodman, R. C. Glen and J. B. O. Mitchell, Mol. Pharmaceutics, 2008, 5, 266 CrossRef CAS PubMed.
- J. Alsenz and M. Kansy, Adv. Drug Delivery Rev., 2007, 59, 546 CrossRef CAS PubMed.
- A. Drews, S. Bovens, K. Roebrock, C. Sunderkötter, D. Reinhardt, M. Schäfers, A. van der Velde, A. S. Elfringhoff, J. Fabian and M. Lehr, J. Med. Chem., 2010, 53, 5165 CrossRef CAS PubMed.
- R. Gozalbes, M. Jacewicz, R. Annand, K. Tsaioun and A. Pineda-Lucena, Bioorg. Med. Chem., 2011, 19, 2615 CrossRef CAS PubMed.
- R. S. Obach, F. Lombardo and N. J. Waters, Drug Metab. Dispos., 2008, 36, 1385 CrossRef CAS PubMed.
- L. J. Jolivette and K. W. Ward, J. Pharm. Sci., 2005, 94, 1467 CrossRef CAS PubMed.
- M. V. S. Varma, B. Feng, R. S. Obach, M. D. Troutman, J. Chupka, H. R. Miller and A. El-Kattan, J. Med. Chem., 2009, 52, 4844 CrossRef CAS PubMed.
- K. A. Connors, in Chemical Kinetics. The Study of Reaction Rates in Solution, VCH Publishers, New York, 1990, pp. 59–131 Search PubMed.
- Source packages for the insilicolynxdqi Python library are available on the Python Package Index (PyPi), https://pypi.python.org/pypi/insilicolynxdqi.
- D. M. Mudie, K. Murray, C. L. Hoad, S. E. Pritchard, M. C. Garnett, G. L. Amidon, P. A. Gowland, R. C. Spiller, G. E. Amidon and L. Marciani, Mol. Pharmaceutics, 2014, 11, 3039 CrossRef CAS PubMed.
- M. Rowland and T. N. Tozer, in Clinical Pharmacokinetics: Concepts and Applications, Lippincott Williams and Wilkins, Pennsylvania, 3rd edn, 1995, pp. 313–339 Search PubMed.
- L. P. Degen and S. F. Phillips, Gut, 1996, 39, 299 CrossRef CAS PubMed.
- T. T. Kararli, Biopharm. Drug Dispos., 1995, 16, 351 CrossRef CAS PubMed.
- Y. Kwon, in Handbook of Essential Pharmacokinetics, Pharmacodynamics, and Drug Metabolism for Industrial Scientists, Kluwer Academic/Plenum Publishers, New York, 2001, p. 233 Search PubMed.
- M. C. Wenlock, Med. Chem. Commun., 2016, 7, 706 RSC.
- Y. Kwon, in Handbook of Essential Pharmacokinetics, Pharmacodynamics, and Drug Metabolism for Industrial Scientists, Kluwer Academic/Plenum Publishers, New York, 2001, p. 65 Search PubMed.
- H. F. Helander and L. Fändriks, Scand. J. Gastroenterol., 2014, 49, 681 CrossRef PubMed.
- D. M. Mudie, G. L. Amidon and G. E. Amidon, Mol. Pharmaceutics, 2010, 7, 1388 CrossRef CAS PubMed.
- E. Sjögren, J. Westergren, I. Grant, G. Hanisch, L. Lindfors, H. Lennernäs, B. Abrahamsson and C. Tannergren, Eur. J. Pharm. Sci., 2013, 49, 679 CrossRef PubMed.
- K. M. Page, Mol. Pharmaceutics, 2016, 13, 609 CrossRef CAS PubMed.
- M. Rowland and T. N. Tozer, in Clinical Pharmacokinetics: Concepts and Applications, Lippincott Williams and Wilkins, Pennsylvania, 3rd edn, 1995, pp. 83–105 Search PubMed.
- M. C. Wenlock and P. Barton, Mol. Pharmaceutics, 2013, 10, 1224 CrossRef CAS PubMed.
- M. C. Wenlock and L. A. Carlsson, J. Chem. Inf. Model., 2015, 55, 125 CrossRef CAS PubMed.
- M. Schulz, S. Iwersen-Bergmann, H. Andresen and A. Schmoldt, Crit. Care, 2012, 16, R136 CrossRef PubMed Data distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0). The lowest value of multiple values was used.
Footnote |
| † Electronic supplementary information (ESI) available: (1) A file containing the raw data for Table 1; (2) a file containing details of the mathematical equations associated to the PK models discussed; (3) a file containing the raw data for eqn (2); (4) a file containing the summary of raw data for Fig. 3 and 4a; (5) a file containing the summary of raw data for Fig. 4b; (6) a file containing the plot data for Fig. 4a and b, 5, 7 and 8a and b; (7) a file containing the command line code for the insilicolynxdqi Python library to replicate the raw data; (8) a file containing the required input data formatted for use with the insilicolynxdqi Python library. See DOI: 10.1039/c7md00586e |
| This journal is © The Royal Society of Chemistry 2018 |