DOI:
10.1039/C7LC01283G
(Paper)
Lab Chip, 2018,
18, 1035-1046
Inertial manipulation of bubbles in rectangular microfluidic channels†
Received
30th November 2017
, Accepted 2nd February 2018
First published on 7th March 2018
Abstract
Inertial microfluidics is an active field of research that deals with crossflow positioning of the suspended entities in microflows. Until now, the majority of the studies have focused on the behavior of rigid particles in order to provide guidelines for microfluidic applications such as sorting and filtering. Deformable entities such as bubbles and droplets are considered in fewer studies despite their importance in multiphase microflows. In this paper, we show that the trajectory of bubbles flowing in rectangular and square microchannels can be controlled by tuning the balance of forces acting on them. A T-junction geometry is employed to introduce bubbles into a microchannel and analyze their lateral equilibrium position in a range of Reynolds (1 < Re < 40) and capillary numbers (0.1 < Ca < 1). We find that the Reynolds number (Re), the capillary number (Ca), the diameter of the bubble (![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) ), and the aspect ratio of the channel are the influential parameters in this phenomenon. For instance, at high Re, the flow pushes the bubble towards the wall while large Ca or
), and the aspect ratio of the channel are the influential parameters in this phenomenon. For instance, at high Re, the flow pushes the bubble towards the wall while large Ca or ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) moves the bubble towards the center. Moreover, in the shallow channels, having aspect ratios higher than one, the bubble moves towards the narrower sidewalls. One important outcome of this study is that the equilibrium position of bubbles in rectangular channels is different from that of solid particles. The experimental observations are in good agreement with the performed numerical simulations and provide insights into the dynamics of bubbles in laminar flows which can be utilized in the design of flow based multiphase flow reactors.
moves the bubble towards the center. Moreover, in the shallow channels, having aspect ratios higher than one, the bubble moves towards the narrower sidewalls. One important outcome of this study is that the equilibrium position of bubbles in rectangular channels is different from that of solid particles. The experimental observations are in good agreement with the performed numerical simulations and provide insights into the dynamics of bubbles in laminar flows which can be utilized in the design of flow based multiphase flow reactors.
1. Introduction
Multiphase flows are of critical importance in systems which transcend the boundaries of a single discipline. In thermal engineering, phase change heat sinks provide higher heat transfer rates and uniform surface temperatures compared to their single phase counterparts.1 A large number of studies have investigated the performance of these heat sinks for electronic cooling.2–5 In the field of reactor engineering, variants of reactors including trickle-bed,6 fluidized bed,7 and bubble column reactors8 rely on multiphase flows to enhance mass transport which requires a thorough understanding of their complex physics. Moreover, in most electrochemical systems, gaseous products evolve at the interface of the electrodes and the electrolyte, including important processes such as water electrolysis,9 chlor-alkali10 and aluminum production.11 Better understanding and control of the phenomena associated with multiphase flows will contribute to improving the performance of these devices. For instance, many electrochemical reactors use ion conducting membranes or porous separators between the anodic and cathodic half cells. Recently, we have shown that by tuning the flow rate of a liquid electrolyte in a microfluidic electrolyzer, it is possible to control the trajectory of the generated bubbles in a membrane-less configuration.12 Removing the solid membrane in these systems decreases the ohmic losses and provides flexibility in the selection of catalysts in addition to a simplified cell design.13–16 Controlling two-phase flows by topography induced variations of the bubbles' surface energy is another way of eliminating the need for a functional membrane.17 In this paper, we implement experimental and numerical tools to investigate the dynamics of bubbles flowing in microfluidic channels. By doing so we are able to determine the key parameters such as the diameter of the bubble, the channel geometry, and the capillary and Reynolds numbers that influence the position of bubbles in the microchannels and provide insights into how to control the bubbles' motion in the flow.
A large body of research in the field of inertial microfluidics has been dedicated to controlling the position of particles in fluidic channels since the discovery of the Segre–Silberberg effect.18,19 Most of the effort in this field is focused on the control of solid particles with diameters smaller than the size of the channel; typically, by one order of magnitude.20–30 Although there are similarities between the behavior of rigid particles and bubbles, deformation of the bubbles31–34 complicates the understanding of the physical phenomena evidenced in gas/liquid flows.
Understanding the active forces affecting bubble motion is necessary in order to explain its behavior. Important forces at moderate Re (1 < Re < 100) are the wall-induced lift force, the shear gradient lift force, and the deformation-induced lift force. These forces are shown schematically in Fig. 1. In this range of Re numbers and length scales, the buoyancy lift force can be neglected since the inertial forces dominate by at least one order of magnitude. The wall-induced lift force originates from the asymmetry in the flow field around the bubble and its direction is towards the center of the channel.35 This force decreases as the bubble moves further away from the wall since the flow asymmetry decreases. The shear gradient lift force is a result of the non-uniform velocity profile and pushes the bubble towards the wall.32,36 The non-uniform velocity profile induces unequal relative velocities on the two sides of the bubble and as a result, it changes the pressure distribution around the bubble. In the parabolic velocity profile, the relative velocity of the flow to the bubble is higher at the closer edge to the wall resulting in a smaller pressure at this side. Therefore, the bubble moves towards the wall where the magnitude of the relative velocity is the highest.37 Deformation of the bubble induces a force towards the centerline where the bubble can minimize its energy by reducing its deviation from the original spherical shape and gain a symmetric shape.38–40 This force is considered as a deformation-induced lift force. The balance of these forces determines the equilibrium bubble position in the crossflow direction.
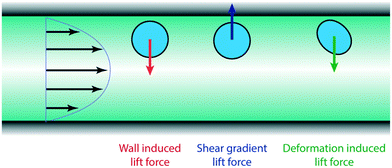 |
| | Fig. 1 Forces acting on the bubble: a wall-induced lift directing towards the centerline which diminishes as the bubble moves away from the wall, a shear gradient lift that pushes the bubble towards the wall, and a deformation-induced lift pointing towards the centerline which becomes stronger as the bubble deformation increases. | |
Numerical and experimental investigations31,33 have confirmed the presence of the deformation-induced, wall and inertial lift forces on the droplets moving in microchannels. As will be discussed in the numerical simulation section, the non-dimensionalized governing equations depend on the Re and Ca numbers. The Re number in the channel flow is an important parameter which determines the relative importance of the lift forces. The flow of the buoyant droplets and bubbles in microfluidic channels has been investigated recently by Stan, et al.32 at low Re. Under these conditions, the forces including buoyancy, deformation-induced, wall, and inertial lift forces have comparable magnitudes.32 In their research, the bubble position is determined by balancing the buoyant force with hydrodynamic lift forces, while at higher Re, the balance of forces acting on the bubble is different. In the study of Rivero-Rodriguez and Scheid,40 the motion of an unconfined bubble in circular microchannels is investigated analytically and numerically. Although their results confirm the effect of inertial and deformation-induced lift forces, the motion of the bubble in the rectangular microchannels is not included in their study.
In this paper, we investigate the bubble motion at moderate Re (1 < Re < 40). We find that by moving towards larger Re, the inertial lift force starts to dominate and gradually changes the equilibrium position. The bubble position in this range of Re is determined by balancing the inertial lift forces with the wall and deformation-induced lift forces, as the effect of the buoyant force is negligible. We use experiments and numerical simulations to investigate systematically the interplay of the bubble diameter, Re, Ca, and the channel geometry in determining the steady state position of the bubbles. We demonstrate that in the channels with aspect ratios higher than one or at high Re, the bubbles stay close to the wall while increasing the Ca or the bubble diameter causes the bubbles to migrate towards the centerline. We discovered that the behavior of the bubble in the rectangular channels is different from the solid particles and this behavior can be modified by using surfactants.
2. Experimental setup
A T-junction geometry is fabricated to introduce nitrogen bubbles from a narrow side channel into the wide main channel as shown in Fig. 2. Microfabrication of the channels starts on a double-sided silicon (Si) wafer with a 1.5 μm silicon dioxide (SiO2) layer on both sides. Two photolithography steps are performed on the topside of the wafer to enable different channel depths for the main and side channels. A third photolithography step is used on the backside to make through holes as fluidic access ports. Channels and ports are fabricated using deep reactive ion etching (DRIE). After etching, a 100 nm layer of silicon dioxide is grown on the silicon wafer. Finally, channels are sealed by bonding the silicon wafer to a Borofloat 33 glass wafer via anodic bonding. Fig. S1 (ESI†) illustrates the complete microfabrication procedure. In order to study the effect of geometry, three sets of channels are fabricated with a depth of 50 μm and widths of 50, 150, and 200 μm. The gas channel is perpendicular to the main channel and its depth and width are both 5 μm. The main channel's length is 16 mm and the gas channel connects to the main channel at the midpoint along the direction of flow. There are two inlets for injecting the liquid and the gas and one outlet for both phases.
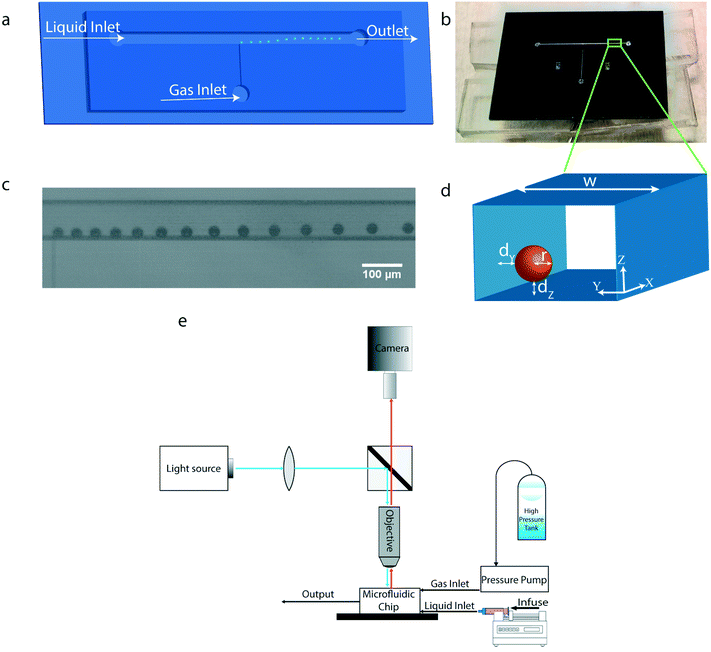 |
| | Fig. 2 Microfluidic device showing (a) a schematic representation of the channel geometry, (b) a photograph of the fabricated device, (c) an image of the bubble formation at the T-junction, and (d) a cross-sectional representation depicting how the radius of the bubble, r, and the bubble distance from the wall, dY, are measured at 6 mm downstream of the T-junction. (e) Experimental setup: the liquid is injected using a syringe pump and a constant pressure pump is used to introduce the gas phase into the device. Motion of bubbles is recorded with a high speed camera in the reflection mode. | |
The flow rate of the liquid and the pressure of the gas are regulated to produce different bubble radii in a wide range of Re values, while Ca is changed by employing different liquids as the carrier phases. Table 1 lists the properties of water, ethanol (Thommen-Furler AG), and isopropanol (Fisher Scientific UK) which are used as carrier phases. The surface tension coefficients of the liquids are measured using a KRUSS DSA-30 drop shape analyzer using the pendant drop method.41 Gas bubbles are generated at the side of the channel. A syringe pump (Cronus Sigma 1000 Series) and a constant pressure pump (Elveflow OB1 MK3) are used for introducing liquid and gas phases, respectively. Bubble properties are measured at a position 6 mm downstream of the T-junction. Videos are recorded using a high-speed camera (Photron FASTCAM Mini UX100) with a frame rate of up to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 fps. The schematic of the experimental setup is depicted in Fig. 2e. The recorded video is used to measure the bubble's distance to the side and the bubble radius in each frame. Diagrams of the bubble position with the error bars representing the standard deviation from the average value are shown in Fig. S2 (ESI†). Based on the measured values, the following parameters are used to define the bubble position for convenience:
000 fps. The schematic of the experimental setup is depicted in Fig. 2e. The recorded video is used to measure the bubble's distance to the side and the bubble radius in each frame. Diagrams of the bubble position with the error bars representing the standard deviation from the average value are shown in Fig. S2 (ESI†). Based on the measured values, the following parameters are used to define the bubble position for convenience:
| | 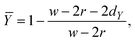 | (1) |
| | 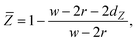 | (2) |
where
w,
r,
dY, and
dZ are the width of the channel, the radius of the bubble, the minimum distance between the bubble's edge to the wall in the
y-direction, and that in the
z-direction, respectively. According to these definitions,
Ȳ and
![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif)
are unit-less quantities that vary from zero to one as the bubble moves from the wall towards the center. Furthermore, it should be noted that the diameter of the bubble is normalized to the channel width:
| | 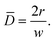 | (3) |
Table 1 Properties of the liquids used as carrier phases: density and viscosity are given at room temperature and atmospheric pressure, and surface tension is measured using a pendant drop method
|
|
Density (kg m−3) |
Viscosity (m2 s−1) |
Surface tension (N m−1) |
| Water |
998.2 |
1.01 × 10−3 |
0.073 |
| Ethanol (Thommen-Furler AG) |
789.4 |
1.14 × 10−3 |
0.022 |
| Isopropanol (Fisher Scientific UK) |
790 |
2.1 × 10−3 |
0.021 |
3. Numerical simulation
We carry out simulations in COSMOL Multiphysics. It resolves the fluid interface by the arbitrary Lagrangian Eulerian (ALE) moving mesh technique, where the interface is represented by exact mesh lines body-fitted with the bubble.
The nondimensional incompressible Navier–Stokes equations solved using COMSOL are:
| | 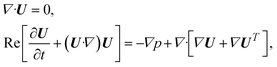 | (4) |
where
p is the pressure and
U is the velocity. Re denotes the ratio of the inertial forces to the viscous forces as:
| | 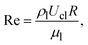 | (5) |
where
μl is the viscosity of the liquid,
ρl is the density of the liquid,
Ucl is the centerline velocity of the underlying flow, and
R is the radius of the bubble at rest. The boundary condition at the interface can be written as:
| | 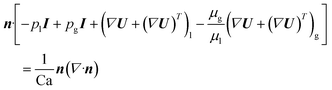 | (6) |
where
n is the unit normal vector to the bubble interface,
I is the unit tensor, and the l and g subscripts denote the liquid and the gas phases, respectively. The capillary number Ca compares the viscous forces against the capillary forces:
| | 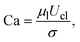 | (7) |
where
σ is the surface tension at the interface. Because the viscosity ratio
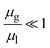
,
eqn (6) can be simplified as follows:
| | 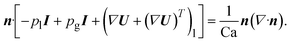 | (8) |
Since the volume of the bubble is supposed to be constant, the pressure pg can be obtained by imposing an additional constraint where the surface integral of the normal velocity on the bubble interface is zero:
We perform the simulations in the reference frame that has the same streamwise translational velocity Ububble of the bubble. In this frame, the velocity imposed on the wall is Ububbleex. At the inlet, the analytical velocity profile (shifted by −Ububble) of a rectangular duct is applied; hence the mean inlet velocity is (Umean − Ububble)ex, where Umean is the average velocity of the underlying flow. The advantage of adopting this frame is that the bubble only translates in the spanwise direction, viz., in the plane normal to the streamwise direction and is hence not advected out of the computational domain but still allowed to freely rotate and deform. This also significantly alleviates the need for expensive remeshing and interpolation which have been the main hurdles of ALE-based simulations. Note that Ububble is a time-dependent unknown obtained at every time step, and it is subject to an additional constraint where the surface integral of the streamwise velocity on the bubble interface is zero. We launch the simulation by initially putting a spherical bubble slightly away from the center of the domain. After a transient period (see Fig. 3), the bubble will reach an equilibrium state, where Ububble, the shape and the lateral position of the bubble do not vary with time. We do not attempt to resolve the transient phase of the dynamics, because in this chosen reference frame, the underlying flow changes the magnitude with time, introducing an artificial acceleration term that will influence the transient dynamics. Luckily, we only focus on the equilibrium configuration of the bubble when it reaches a steady velocity Usteadybubble and hence the artificial acceleration term vanishes without influencing the equilibrium dynamics. To confirm that the equilibrium configuration is independent of the transient dynamics, we have conducted for certain cases a new computation where the velocities towards the wall and in the inlet are shifted by a time-invariant magnitude, Usteadybubble. The new equilibrium configuration is the same as the previous one, confirming that our strategy is appropriate.
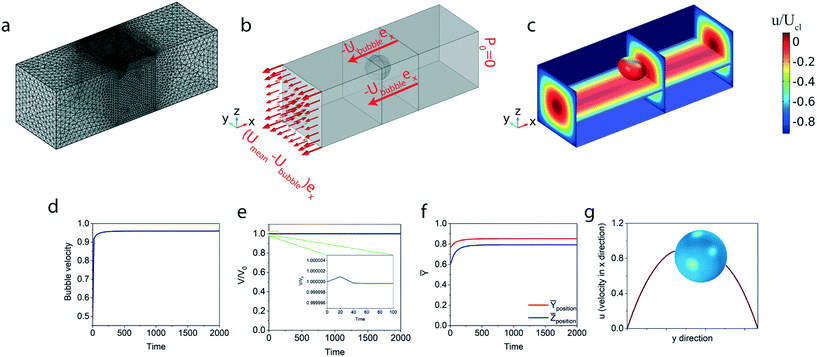 |
| | Fig. 3 Computational setup: (a) the computational mesh used in the numerical simulation. (b) In the streamwise direction, the reference frame is applied on the bubble. Hence a velocity shift of Ububble in the −ex direction is applied on both the walls and the inlet boundary. (c) The streamwise velocity at different cross sections of the duct when the bubble reaches its equilibrium position. (d) The time evolution of bubble velocity indicates that the bubble reaches its equilibrium position. (e) The volume of the bubble is monitored to guarantee its time invariance. The bubble's lateral position (f) and velocity profile around the bubble (g) are extracted from the equilibrium solution. | |
We span a wide range of the three nondimensional numbers Re, Ca, and ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) for a thorough computational investigation. Fig. 3 shows the computational setup and results. The velocity of the bubble is monitored as a function of time to make sure that the solution converges to the steady state. To verify the conservation of the bubble's volume, the temporal evolution of the bubble's volume is plotted in Fig. 3e. After verifying that the equilibrium state has been reached, the bubble position and the velocity profile around the bubble are extracted and shown in Fig. 3f and g, respectively.
for a thorough computational investigation. Fig. 3 shows the computational setup and results. The velocity of the bubble is monitored as a function of time to make sure that the solution converges to the steady state. To verify the conservation of the bubble's volume, the temporal evolution of the bubble's volume is plotted in Fig. 3e. After verifying that the equilibrium state has been reached, the bubble position and the velocity profile around the bubble are extracted and shown in Fig. 3f and g, respectively.
4. Validation of simulations
Recently, COMSOL Multiphysics has been used for simulation of droplets in circular geometries where the results are in good agreement with the asymptotic analysis and the boundary integral method which shows its capability in resolving the droplet motion.42 Table S1† shows the results of the numerical simulations for different grid sizes. The grid parameter sizes of the third simulation are optimal and chosen for the numerical study. In this section, for validation of the numerical simulations with the experiments, simulations are performed over the same range of Re, ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) , and Ca as in experiments. Experimental data are selected for both of the cases where bubbles go to the center or to the wall. Also, data are chosen from two different types of liquids to probe the impact of Ca. The comparison between the two sets of results is summarized in Table 2 with isopropanol as the carrier fluid and Table 3 with ethanol as the carrier fluid. In the tables, Ȳ and
, and Ca as in experiments. Experimental data are selected for both of the cases where bubbles go to the center or to the wall. Also, data are chosen from two different types of liquids to probe the impact of Ca. The comparison between the two sets of results is summarized in Table 2 with isopropanol as the carrier fluid and Table 3 with ethanol as the carrier fluid. In the tables, Ȳ and ![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) are calculated using eqn (1) and (2). At Re ≤ 1.29, the predicted bubble position from the simulations does not correspond to the experimental values. This discrepancy can be explained by considering the possibility that multiple equilibrium positions exist in the channel.33 As a result, it is possible that the simulation chooses one of the equilibrium positions and the experiment the other. More importantly, in the experiments, a row of bubbles can be seen, while a single bubble motion is simulated numerically. At low Re, the range of influence of a bubble increases; promoting inter-bubble interactions that can affect the lateral position of the bubble.43 At higher values of Re and Ca, excellent agreement can be seen between simulations and experiments. Table 4 shows the numerical results for the equilibrium position of the bubbles with different initial positions. The results show that the bubble, starting from different positions, reaches the same equilibrium position. However, this result cannot be considered as a general statement since at low Re, a bubble can possibly have multiple equilibrium positions as seen for solid particles.44
are calculated using eqn (1) and (2). At Re ≤ 1.29, the predicted bubble position from the simulations does not correspond to the experimental values. This discrepancy can be explained by considering the possibility that multiple equilibrium positions exist in the channel.33 As a result, it is possible that the simulation chooses one of the equilibrium positions and the experiment the other. More importantly, in the experiments, a row of bubbles can be seen, while a single bubble motion is simulated numerically. At low Re, the range of influence of a bubble increases; promoting inter-bubble interactions that can affect the lateral position of the bubble.43 At higher values of Re and Ca, excellent agreement can be seen between simulations and experiments. Table 4 shows the numerical results for the equilibrium position of the bubbles with different initial positions. The results show that the bubble, starting from different positions, reaches the same equilibrium position. However, this result cannot be considered as a general statement since at low Re, a bubble can possibly have multiple equilibrium positions as seen for solid particles.44
Table 2 Bubble equilibrium positions when the carrier fluid is isopropanol
| Re |
0.48 |
0.51 |
2.11 |
2.60 |
2.66 |
7.37 |
9.48 |
10.60 |
| Ca |
0.007 |
0.007 |
0.035 |
0.035 |
0.046 |
0.162 |
0.162 |
0.162 |
![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif)
|
0.74 |
0.78 |
0.64 |
0.78 |
0.60 |
0.48 |
0.61 |
0.69 |
|
Ȳ
experiment
|
1.00 |
1.00 |
0.52 |
1.01 |
0.52 |
0.36 |
0.48 |
0.77 |
|
Ȳ
simulation
|
0.80 |
0.95 |
0.53 |
0.96 |
0.48 |
0.36 |
0.50 |
0.80 |
![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) simulation
simulation
|
0.88 |
0.86 |
0.56 |
0.96 |
0.50 |
0.36 |
0.50 |
0.83 |
Table 3 Bubble equilibrium positions when the carrier fluid is ethanol
| Re |
1.29 |
1.68 |
4.53 |
6.22 |
11.07 |
15.13 |
13.62 |
18.77 |
| Ca |
0.006 |
0.006 |
0.024 |
0.024 |
0.059 |
0.059 |
0.071 |
0.071 |
![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif)
|
0.64 |
0.84 |
0.56 |
0.78 |
0.55 |
0.75 |
0.57 |
0.78 |
|
Ȳ
experiment
|
0.13 |
0.99 |
0.09 |
0.32 |
0.17 |
0.34 |
0.14 |
0.36 |
|
Ȳ
simulation
|
0.69 |
0.86 |
0.19 |
0.44 |
0.19 |
0.38 |
0.19 |
0.54 |
![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) simulation
simulation
|
0.81 |
0.88 |
0.24 |
0.45 |
0.20 |
0.38 |
0.19 |
0.54 |
Table 4 Numerical simulation of the bubble equilibrium position with different initial positions
Re = 2.60 Ca = 0.035 ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) = 0.78 = 0.78 |
Re = 9.48 Ca = 0.162 ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) = 0.61 = 0.61 |
| Initial position |
Equilibrium position |
Initial position |
Equilibrium position |
|
Ȳ = 0.71 |
Ȳ = 0.96 |
Ȳ = 0.87 |
Ȳ = 0.50 |
![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) = 0.82 = 0.82 |
![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) = 0.96 = 0.96 |
![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) = 0.92 = 0.92 |
![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) = 0.51 = 0.51 |
|
Ȳ = 0.60 |
Ȳ = 0.96 |
Ȳ = 0.67 |
Ȳ = 0.50 |
![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) = 0.64 = 0.64 |
![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) = 0.96 = 0.96 |
![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) = 0.78 = 0.78 |
![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) = 0.50 = 0.50 |
|
Ȳ = 0.42 |
Ȳ = 0.94 |
Ȳ = 0.46 |
Ȳ = 0.50 |
![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) = 0.45 = 0.45 |
![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) = 0.93 = 0.93 |
![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) = 0.57 = 0.57 |
![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) = 0.50 = 0.50 |
5. Results
The influence of Re, Ca, the bubble diameter and the channel geometry on the positioning of the bubbles merits a detailed discussion. In the following subsections, each parameter's role is discussed and in the last part, the equilibrium position of the bubbles is compared with the solid particles.
1. Effect of the Reynolds number
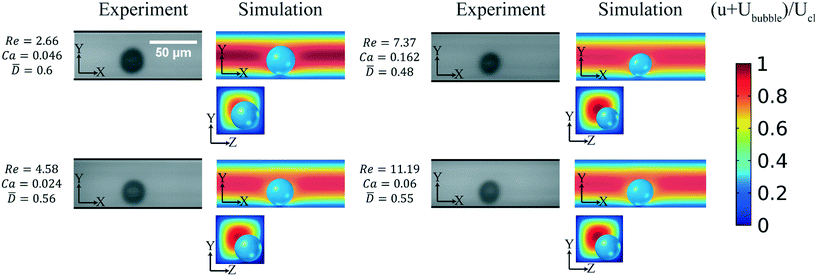
The Reynolds number determines the balance of the different forces acting on the bubble. The shear gradient lift force towards the wall depends on the relative velocity at the two sides of the bubble. By increasing the Re, the difference in relative velocity at the two sides of the bubble increases and as a result, the shear gradient lift force increases. The higher relative velocity near the wall generally translates to lower pressure on the side of the bubble facing the wall; therefore, this force dominates at higher Re, pushing the bubbles towards the wall. Fig. 4 shows the effect of the Re in the 50 μm wide channel. At small Re values, the bubble equilibrium position is at the centerline. Fig. 5 shows the numerical results for the bubble's lateral position at different Re values for Ca = 0.1 and ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) = 0.4. In each simulation, the bubble's initial position is at (Ȳ,
= 0.4. In each simulation, the bubble's initial position is at (Ȳ, ![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) ) = (0.7667, 0.6). As the Re increases, the bubble moves closer to the wall and at Re larger than 20, the bubble moves to the corner of the channel on the diagonal.
) = (0.7667, 0.6). As the Re increases, the bubble moves closer to the wall and at Re larger than 20, the bubble moves to the corner of the channel on the diagonal.
 |
| | Fig. 4 Effect of Re on the lateral position of the bubble: experimental results and the corresponding numerical simulations are for the channel with 50 μm width and 50 μm depth. The bubble diameter is normalized to the channel width. By increasing the Re, the bubble moves gradually towards the wall. | |
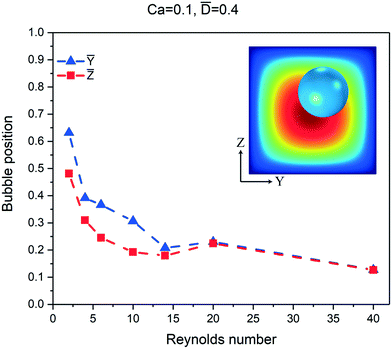 |
| | Fig. 5 Numerical results of the Reynolds number's effect on the lateral position of a bubble in a square channel. The blue points and the red points show the equilibrium position of the bubble in the horizontal and vertical directions, respectively. All simulations are carried out for ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) = 0.4 and Ca = 0.1. The initial bubble position is at (Ȳ, = 0.4 and Ca = 0.1. The initial bubble position is at (Ȳ, ![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) ) = (0.7667, 0.6). ) = (0.7667, 0.6). | |
2. Effect of the capillary number
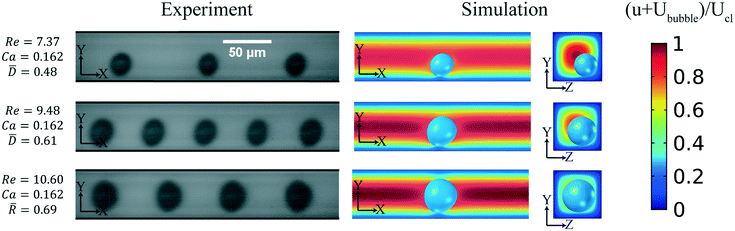
The capillary number signifies the ratio of viscous forces to the surface tension forces. At large Ca, the viscous forces are stronger than the capillary forces and a bubble under this condition undergoes larger deformation. The minimum surface energy for the bubble is achieved in the spherical shape. This condition is best met when the bubble is in the middle of the channel where the velocity profile is symmetric and the velocity is the same on both sides of the bubble. As a result, the flow exerts stronger deformation-induced lift force on the bubble towards the center of the channel. Fig. 6 shows the bubble position at different Ca values. In this figure, the continuous phases in the first and second rows are isopropanol and ethanol, respectively. The Ca is larger in the first row and as a result, the distance between the bubble and the wall is larger in the first row. Numerical results at different Ca values with Re = 10 and ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) = 0.4 are shown in Fig. 7. The bubble equilibrium position is closer to the centerline at larger Ca. At Ca higher than 0.9, the bubble moves to the centerline.
= 0.4 are shown in Fig. 7. The bubble equilibrium position is closer to the centerline at larger Ca. At Ca higher than 0.9, the bubble moves to the centerline.
 |
| | Fig. 6 Effect of the Ca on the bubble position for the square channel: the carrier fluid in the first row is isopropanol and that in the second row is ethanol. Ca has a smaller value when the carrier fluid is ethanol and as a result, the bubble is closer to the wall. As the Ca increases, the bubble moves further away from the wall. The channel's cross sectional dimensions in the experiments are 50 μm by 50 μm. Numerical simulations, corresponding to the same parameters, support the experimental results. The color bar shows the velocity in the flow direction which is normalized by the centerline velocity. | |
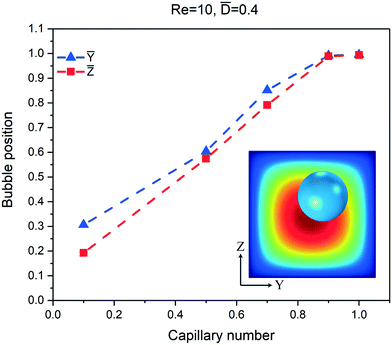 |
| | Fig. 7 Numerical results for the square channel at different Ca values, while the Re and ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) are constant. The initial position of the bubble is (Ȳ, are constant. The initial position of the bubble is (Ȳ, ![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) ) = (0.7667, 0.6). The blue points and the red points show the equilibrium positions of the bubble in the horizontal and vertical directions, respectively. As the Ca number increases the bubble moves closer to the center and at Ca > 0.9 the bubble moves exactly to the center. ) = (0.7667, 0.6). The blue points and the red points show the equilibrium positions of the bubble in the horizontal and vertical directions, respectively. As the Ca number increases the bubble moves closer to the center and at Ca > 0.9 the bubble moves exactly to the center. | |
3. Effect of the bubble's diameter
Lateral forces acting on the bubble originate from unequal pressure and velocity around the bubble. These parameters change as the diameter of the bubble varies. Fig. 8 presents the effect of bubble diameter on its equilibrium position. It can be observed that the larger bubble is closer to the channel's centerline. Fig. 9 shows the results of the simulations for various bubble diameters at constant Re = 10 and Ca = 0.1. The equilibrium position of a bubble smaller than half of the channel is between the diagonal line and the center of the sidewall. On the one hand, such a bubble moves towards the center of the sidewall similar to a small solid particle.45 On the other hand, the deformation-induced lift force pushes the bubble towards the diagonal line where the shear stress is smaller as shown in Fig. S5.† Therefore, as the diameter of the bubble decreases, the deformability of the bubble decreases and the equilibrium position of the bubble moves closer to the center of the sidewall. When the bubble diameter becomes larger than half of the width of the channel, the bubble moves along the diagonal and by increasing the diameter of the bubble, eventually, it moves to the centerline of the channel. Larger bubbles feel stronger wall-induced lift force towards the center and besides that, when the diameter of the bubble exceeds half of the channel width, the shear gradient lift force towards the wall decreases. Therefore, as the bubble becomes larger, forces towards the center dominate and the shear gradient lift force towards the wall diminishes resulting in positioning of the bubble at the centerline.
 |
| | Fig. 8 Effect of the bubble's radius on the equilibrium position: experimental results for a channel with 50 μm width and 50 μm depth are compared with the corresponding simulations in color. The color map shows the normalized velocity of the flow in the x-direction. The results show that the equilibrium position of larger bubbles is closer to the centerline than that of smaller bubbles. | |
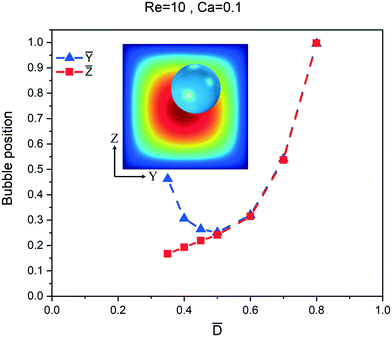 |
| | Fig. 9 Numerical simulations of different bubble diameters for the square channel at constant Re = 10 and Ca = 0.1. The initial position of the bubble is at (Ȳ, ![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) ) = (0.7667, 0.6). The equilibrium position of a bubble that is smaller than half of the channel width is close to the wall. A bubble larger than half of the channel width moves along the diagonal of the channel and by increasing the diameter of the bubble, it eventually moves to the center of the channel. ) = (0.7667, 0.6). The equilibrium position of a bubble that is smaller than half of the channel width is close to the wall. A bubble larger than half of the channel width moves along the diagonal of the channel and by increasing the diameter of the bubble, it eventually moves to the center of the channel. | |
4. Effect of aspect ratio of the channel
As discussed in the previous section, bubbles with diameters larger than half of the channel width with a square geometry move towards the center. In the channels with aspect ratios larger than one, the bubble diameter can be larger than half of the height and smaller than half of the width of the channel. Therefore, the bubble moves towards the center in the height direction and moves towards the wall in the width direction. Fig. 10 shows the experimental and numerical results for channels with different aspect ratios. In the square channel, since the bubble diameter is larger than half of the channel's width, it moves to the centerline. In the channels with aspect ratios larger than one, the equilibrium position of the bubble changes from the centerline to the narrower side of the channel. Fig. 11 shows the experimental results for channels with three different aspect ratios. In the square channel, bubbles can be in the center of the channel or close to the wall based on their diameters. As discussed in section 3, for bubbles with larger diameter, the forces towards the center increases and push the bubbles to the center while smaller bubbles move to the wall. On the other hand, in the rectangular channels, the equilibrium position of the bubbles with the same diameters is close to the narrow side of the channel.
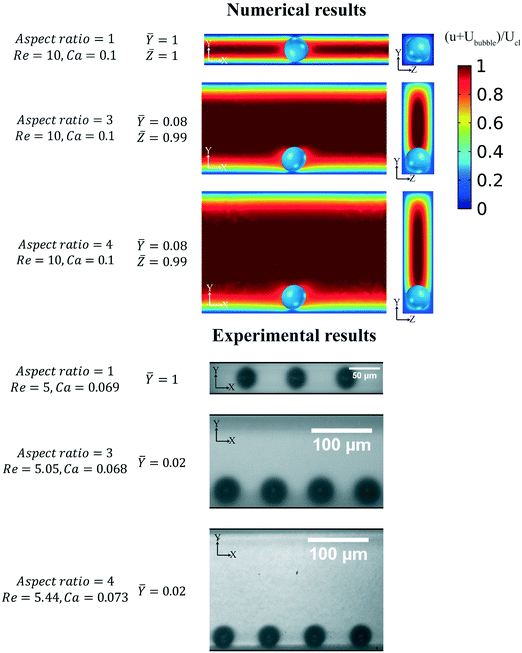 |
| | Fig. 10 Effect of the channel geometry on the lateral position of the bubble while the Re and Ca are constant. Experimental and numerical results show that in the wider channels, the bubble equilibrium position is close to the smaller edge while in the channel with an aspect ratio of one the bubble equilibrium position is in the center. | |
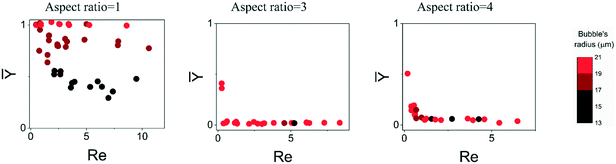 |
| | Fig. 11 Experimental results for three different channel aspect ratios when the carrier fluid is isopropanol. The vertical axis and horizontal axis show the bubble position and Reynolds number, respectively, and the color map indicates the radius of the bubble in μm. In these diagrams, Ȳ = 1 corresponds to the bubble position at the centerline and Ȳ = 0 to the bubble position close to the wall. In the square channel, the bubbles are in the center of the channel or close to the wall based on their diameters, but in the rectangular channels, the equilibrium positions of the bubbles are closer to the smaller sidewall. | |
5. The difference between equilibrium positions of bubbles and particles
As shown in Fig. 11 for the considered parameter range, the equilibrium position of the bubble in a rectangular channel is close to the shallower edge, whereas it is known that the equilibrium position of a rigid particle in a rectangular channel is in the center of the channel's longer wall.35,45–47 The different behavior of the bubble and the solid particle is due to the existence of a rigid particle–fluid interface in the former and a fluid–fluid interface in the latter case. To have a better comparison between the rigid particles and bubbles, it is possible to add a surfactant to the carrier fluid to make the bubbles behave similarly to rigid particles.48,49Fig. 12 shows the equilibrium position of particles when the carrier fluid is water and the equilibrium position of bubbles when the continuous phase is water or a solution of water and a surfactant (a 1% volumetric aqueous solution of Triton X-100) in the channel with 150 μm width. This figure demonstrates that even with a small amount of the surfactant, the bubbles move to the center of the wider channel while at the same Re, bubbles in surfactant-free water stay close to the shallower wall. By adding the surfactant to the liquid, molecules of the surfactant are adsorbed at the interface, making it a no-slip surface. This phenomenon reduces the interaction of the two fluids at the interface and makes the bubbles behave similarly to the rigid particles. Fig. 13 shows the schematic of the equilibrium position of clean bubbles, contaminated bubbles, and solid particles in the cross section of the channel. A clean bubble goes towards the shallower wall while a solid particle or a contaminated bubble stabilizes at the center of the wider sidewalls.45,46
 |
| | Fig. 12 Experimental results show different equilibrium position for bubbles and particles: addition of a small amount of surfactant forces the bubble to behave like a particle. At the same flow rate, the equilibrium positions of contaminated bubbles and solid particles are at the center of the wider channel while clean bubbles stay close to the shallower wall. | |
 |
| | Fig. 13 Schematic of the equilibrium position of a bubble in a clean carrier fluid (left), a bubble in a carrier fluid with surfactants (middle), and a solid particle (right). Different circles show the position of circles at different times (× marks the initial position). The clean bubble goes to the center in the Z direction and moves towards the shallower wall. The solid particle and contaminated bubble move towards the center of the wider channel and stay centered in the Y direction. | |
6. Transition of the bubble position
Given the importance of the Re and Ca, it is of interest to elaborate more on their combined impact on the bubble behavior. Simulations are carried out for a bubble with the diameter of ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) = 0.4 at different combinations of Ca and Re. In the simulations, the bubble is initially positioned at (Ȳ,
= 0.4 at different combinations of Ca and Re. In the simulations, the bubble is initially positioned at (Ȳ, ![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) ) = (0.7667, 0.6) in a square channel. Color coding the equilibrium position of the bubble in Fig. 14 for different Ca and Re values helps to highlight the transition zone of the bubble position from the center to the wall. This figure displays that at high Re, the bubble moves to the wall (small Ȳ) while at high Ca the bubble moves to the centerline (large Ȳ). This diagram helps in predicting the bubble position in the channel under different flow conditions. Analogous diagrams can be drawn for different bubble diameters using the proposed numerical tool.
) = (0.7667, 0.6) in a square channel. Color coding the equilibrium position of the bubble in Fig. 14 for different Ca and Re values helps to highlight the transition zone of the bubble position from the center to the wall. This figure displays that at high Re, the bubble moves to the wall (small Ȳ) while at high Ca the bubble moves to the centerline (large Ȳ). This diagram helps in predicting the bubble position in the channel under different flow conditions. Analogous diagrams can be drawn for different bubble diameters using the proposed numerical tool.
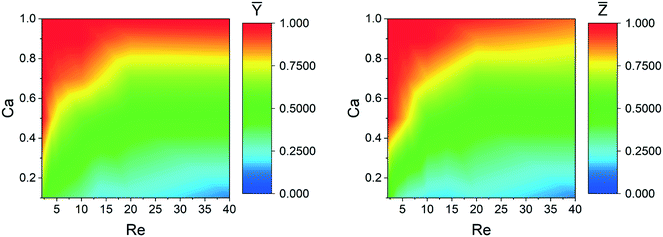 |
| | Fig. 14 Numerical results for the equilibrium position of a bubble with ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) = 0.4 and an initial position of (Ȳ, = 0.4 and an initial position of (Ȳ, ![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) ) = (0.7667, 0.6) in the channel at different Re and Ca values. ) = (0.7667, 0.6) in the channel at different Re and Ca values. | |
6. Conclusion
Monodisperse bubbles' motion in rectangular microchannels was investigated in order to observe their crossflow equilibrium position. The diameter of the bubble, the aspect ratio of the channel, and the Reynolds and capillary numbers are found to be the critical parameters. Analysis of the results reveals the pattern of the changes in the bubbles' position. Both numerical and experimental data show that a high Re flow pushes the bubbles towards the wall. Moreover, bubbles in the channel with an aspect ratio higher than unity move to the shallower sidewall and by increasing the aspect ratio of the channel their distance from the center increases. On the other hand, by increasing the capillary number, the bubble moves close to the center and for bubbles with ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) = 0.4 in a square channel and at capillary numbers higher than 0.9, their equilibrium position is at the centerline. Furthermore, bubbles that have a radius smaller than half of the width of the channel move to the wall while bubbles with a radius larger than half of the channel's width move to the centerline. Finally, the comparison between the equilibrium position of a bubble and a solid particle demonstrates that the shallower wall of the rectangular channel is the equilibrium position of the bubble while the solid particle moves to the center of the wider sidewall. This study provides insights into the effective parameters in the bubble motion and the methods we presented can be employed in designing multiphase microfluidic devices. Future studies on the interactions of bubbles introduced from multiple side channels with various sizes will shed more light on the complex dynamics of bubbly flows.
= 0.4 in a square channel and at capillary numbers higher than 0.9, their equilibrium position is at the centerline. Furthermore, bubbles that have a radius smaller than half of the width of the channel move to the wall while bubbles with a radius larger than half of the channel's width move to the centerline. Finally, the comparison between the equilibrium position of a bubble and a solid particle demonstrates that the shallower wall of the rectangular channel is the equilibrium position of the bubble while the solid particle moves to the center of the wider sidewall. This study provides insights into the effective parameters in the bubble motion and the methods we presented can be employed in designing multiphase microfluidic devices. Future studies on the interactions of bubbles introduced from multiple side channels with various sizes will shed more light on the complex dynamics of bubbly flows.
Conflicts of interest
There are no conflicts of interest to declare.
Acknowledgements
The authors thank Professor Petros Koumoutsakos, Dr. Sergey Litvinov, and Petr Karnakov for helpful and stimulating discussions. This research was supported by the grant no. “CRSII5_173860” of Sinergia for the Multiphase Flow Electrochemical Reactors (MFERS) project (P. H., S. M. H. H., M. A. M., and D. P.), the grant no. “20NA21-145936” of Nano-Tera Initiative for the Solar Hydrogen Integrated Nano Electrolyzer (SHINE) project (P. H., S. M. H. H., M. A. M., and D. P.), ERC grant no. “SIMCOMICS 280117” (G. B. and F. G.), and the VR International Postdoc Grant from Swedish Research Council “2015-06334” (L. Z.). The numerical simulations were performed through the use of the facilities of EPFL Scientific IT and Application Support Center.
References
- J. Lee and I. Mudawar, Two-phase flow in high-heat-flux micro-channel heat sink for refrigeration cooling applications: Part II—heat transfer characteristics, Int. J. Heat Mass Transfer, 2005, 48(5), 941–955 CrossRef CAS.
- C. Green,
et al., A Review of Two-Phase Forced Cooling in Three-Dimensional Stacked Electronics: Technology Integration, J. Electron. Packag., 2015, 137(4), 040802 CrossRef.
- S. G. Kandlikar, History, advances, and challenges in liquid flow and flow boiling heat transfer in microchannels: a critical review, J. Heat Transfer, 2012, 134(3), 034001 CrossRef.
- A. Fazeli, M. Mortazavi and S. Moghaddam, Hierarchical biphilic micro/nanostructures for a new generation phase-change heat sink, Appl. Therm. Eng., 2015, 78, 380–386 CrossRef.
- E. N. Wang,
et al., Micromachined jets for liquid impingement cooling of VLSI chips, J. Microelectromech. Syst., 2004, 13(5), 833–842 CrossRef.
-
V. V. Ranade, R. Chaudhari and P. R. Gunjal, Trickle bed reactors: reactor engineering & applications, Elsevier, 2011 Search PubMed.
-
J. Werther, Fluidized Bed Reactors, Wiley Online Library, 1992 Search PubMed.
- C. Leonard,
et al., Bubble column reactors for high pressures and high temperatures operation, Chem. Eng. Res. Des., 2015, 100, 391–421 CrossRef CAS.
- M. Carmo,
et al., A comprehensive review on PEM water electrolysis, Int. J. Hydrogen Energy, 2013, 38(12), 4901–4934 CrossRef CAS.
- J. Crook and A. Mousavi, The chlor-alkali process: A review of history and pollution, Environ. Forensics, 2016, 17(3), 211–217 CrossRef CAS.
- D. S. Severo,
et al., Modeling magnetohydrodynamics of aluminum electrolysis cells with ANSYS and CFX, Light Met., 2005, 2005, 475–480 Search PubMed.
- S. M. H. Hashemi, M. A. Modestino and D. Psaltis, A membrane-less electrolyzer for hydrogen production across the pH scale, Energy Environ. Sci., 2015, 8(7), 2003–2009 Search PubMed.
- M. A. Modestino, S. M. H. Hashemi and S. Haussener, Mass transport aspects of electrochemical solar-hydrogen generation, Energy Environ. Sci., 2016, 9(5), 1533–1551 CAS.
- D. V. Esposito, Membraneless Electrolyzers for Low-Cost Hydrogen Production in a Renewable Energy Future, Joule, 2017, 651–658 CrossRef.
- G. D. O'Neil,
et al., Hydrogen Production with a Simple and Scalable Membraneless Electrolyzer, J. Electrochem. Soc., 2016, 163(11), F3012–F3019 CrossRef.
- M. A. Modestino,
et al., The potential for microfluidics in electrochemical energy systems, Energy Environ. Sci., 2016, 9(11), 3381–3391 CAS.
- S. Hashemi,
et al., Membrane-less micro fuel cell based on two-phase flow, J. Power Sources, 2017, 348, 212–218 CrossRef CAS.
- G. Segre, Radial particle displacements in Poiseuille flow of suspensions, Nature, 1961, 189, 209–210 CrossRef.
- G. Segre and A. Silberberg, Behaviour of macroscopic rigid spheres in Poiseuille flow Part 2. Experimental results and interpretation, J. Fluid Mech., 1962, 14(01), 136–157 CrossRef.
- D. Di Carlo,
et al., Continuous inertial focusing, ordering, and separation of particles in microchannels, Proc. Natl. Acad. Sci. U. S. A., 2007, 104(48), 18892–18897 CrossRef CAS PubMed.
- A. A. S. Bhagat, S. S. Kuntaegowdanahalli and I. Papautsky, Enhanced particle filtration in straight microchannels using shear-modulated inertial migration, Phys. Fluids, 2008, 20(10), 101702 CrossRef.
- X. Xuan, J. Zhu and C. Church, Particle focusing in microfluidic devices, Microfluid. Nanofluid., 2010, 9(1), 1–16 CrossRef.
- X. Lu and X. Xuan, Continuous microfluidic particle separation via elasto-inertial pinched flow fractionation, Anal. Chem., 2015, 87(12), 6389–6396 CrossRef CAS PubMed.
- M. Jimenez and H. Bridle, Microfluidics for effective concentration and sorting of waterborne protozoan pathogens, J. Microbiol. Methods, 2016, 126, 8–11 CrossRef CAS PubMed.
- C. Xue,
et al., Lateral migration of dual droplet trains in a double spiral microchannel, Sci. China: Phys., Mech. Astron., 2016, 59(7), 1–10 CAS.
- Y.-S. Choi and S.-J. Lee, Holographic analysis of three-dimensional inertial migration of spherical particles in micro-scale pipe flow, Microfluid. Nanofluid., 2010, 9(4–5), 819–829 CrossRef CAS.
- A. A. S. Bhagat,
et al., Inertial microfluidics for sheath-less high-throughput flow cytometry, Biomed. Microdevices, 2010, 12(2), 187–195 CrossRef PubMed.
- A. Karimi, S. Yazdi and A. Ardekani, Hydrodynamic mechanisms of cell and particle trapping in microfluidics, Biomicrofluidics, 2013, 7(2), 021501 CrossRef CAS PubMed.
- A. J. Chung, D. R. Gossett and D. Di Carlo, Three dimensional, sheathless, and high throughput microparticle inertial focusing through geometry induced secondary flows, Small, 2013, 9(5), 685–690 CrossRef CAS PubMed.
- A. A. Kayani,
et al., Optofluidics incorporating actively controlled micro-and nano-particles, Biomicrofluidics, 2012, 6(3), 031501 CrossRef PubMed.
- S. Mortazavi, and G. Tryggvason, A numerical study of the motion of drops in Poiseuille flow. Part 1. Lateral migration of one drop, J. Fluid Mech., 2000, 411, 325–350 CrossRef.
- C. A. Stan,
et al., Sheathless hydrodynamic positioning of buoyant drops and bubbles inside microchannels, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84(3), 036302 CrossRef PubMed.
- X. Chen,
et al., Inertial migration of deformable droplets in a microchannel, Phys. Fluids, 2014, 26(11), 112003 CrossRef.
- S. C. Hur,
et al., Deformability-based cell classification and enrichment using inertial microfluidics, Lab Chip, 2011, 11(5), 912–920 RSC.
- J. Zhang,
et al., Fundamentals and applications of inertial microfluidics: a review, Lab Chip, 2016, 16(1), 10–34 RSC.
- B. Ho and L. Leal, Inertial migration of rigid spheres in two-dimensional unidirectional flows, J. Fluid Mech., 1974, 65(02), 365–400 CrossRef.
- J. M. Martel and M. Toner, Inertial focusing in microfluidics, Annu. Rev. Biomed. Eng., 2014, 16, 371 CrossRef CAS PubMed.
- H. Goldsmith and S. Mason, The flow of suspensions through tubes. I. Single spheres, rods, and discs, J. Colloid Sci., 1962, 17(5), 448–476 CrossRef.
- C. Schaaf and H. Stark, Inertial migration and axial control of deformable capsules, Soft Matter, 2017, 3544–3555 RSC.
-
J. Rivero-Rodriguez and B. Scheid, Bubbles dynamics in microchannels: inertial and capillary migration forces, 2017, arXiv preprint arXiv:1708.01114 Search PubMed.
- A. Daerr and A. Mogne, Pendent_Drop: An ImageJ Plugin to Measure the Surface Tension from an Image of a Pendent Drop, J. Open Res. Softw., 2016, 4(1), e3 Search PubMed.
-
G. Balestra, L. Zhu and F. Gallaire, A viscous droplet in a capillary tube: from Bretherton's theory to empirical models, 2017, arXiv preprint arXiv:1711.10447 Search PubMed.
- Y. Wang and P. Dimitrakopoulos, Low-Reynolds-number droplet motion in a square microfluidic channel, Theor. Comput. Fluid Dyn., 2012, 26(1), 361–379 CrossRef CAS.
- A. A. S. Bhagat, S. S. Kuntaegowdanahalli and I. Papautsky, Enhanced particle filtration in straight microchannels using shear-modulated inertial migration, Phys. Fluids, 2008, 20(10), 101702 CrossRef.
- C. Prohm and H. Stark, Feedback control of inertial microfluidics using axial control forces, Lab Chip, 2014, 14(12), 2115–2123 RSC.
- H. Amini, W. Lee and D. Di Carlo, Inertial microfluidic physics, Lab Chip, 2014, 14(15), 2739–2761 RSC.
- P. Paiè,
et al., Particle focusing by 3D inertial microfluidics, Microsyst. Nanoeng., 2017, 3, 17027 CrossRef.
- S. Takagi and Y. Matsumoto, Surfactant effects on bubble motion and bubbly flows, Annu. Rev. Fluid Mech., 2011, 43, 615–636 CrossRef.
-
R. Clift, J. Grace and M. Webber, Bubbles, drop, and particles, Academic Press, New York, 1978 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7lc01283g |
|
| This journal is © The Royal Society of Chemistry 2018 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
S. Mohammad H.
Hashemi
a,
Gioele
Balestra
a,
S. Mohammad H.
Hashemi
a,
Gioele
Balestra
 b,
Lailai
Zhu
b,
Lailai
Zhu
 cd,
Miguel A.
Modestino
e,
François
Gallaire
cd,
Miguel A.
Modestino
e,
François
Gallaire
 b and
Demetri
Psaltis
*a
b and
Demetri
Psaltis
*a
![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) ), and the aspect ratio of the channel are the influential parameters in this phenomenon. For instance, at high Re, the flow pushes the bubble towards the wall while large Ca or
), and the aspect ratio of the channel are the influential parameters in this phenomenon. For instance, at high Re, the flow pushes the bubble towards the wall while large Ca or ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) moves the bubble towards the center. Moreover, in the shallow channels, having aspect ratios higher than one, the bubble moves towards the narrower sidewalls. One important outcome of this study is that the equilibrium position of bubbles in rectangular channels is different from that of solid particles. The experimental observations are in good agreement with the performed numerical simulations and provide insights into the dynamics of bubbles in laminar flows which can be utilized in the design of flow based multiphase flow reactors.
moves the bubble towards the center. Moreover, in the shallow channels, having aspect ratios higher than one, the bubble moves towards the narrower sidewalls. One important outcome of this study is that the equilibrium position of bubbles in rectangular channels is different from that of solid particles. The experimental observations are in good agreement with the performed numerical simulations and provide insights into the dynamics of bubbles in laminar flows which can be utilized in the design of flow based multiphase flow reactors.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 fps. The schematic of the experimental setup is depicted in Fig. 2e. The recorded video is used to measure the bubble's distance to the side and the bubble radius in each frame. Diagrams of the bubble position with the error bars representing the standard deviation from the average value are shown in Fig. S2 (ESI†). Based on the measured values, the following parameters are used to define the bubble position for convenience:
000 fps. The schematic of the experimental setup is depicted in Fig. 2e. The recorded video is used to measure the bubble's distance to the side and the bubble radius in each frame. Diagrams of the bubble position with the error bars representing the standard deviation from the average value are shown in Fig. S2 (ESI†). Based on the measured values, the following parameters are used to define the bubble position for convenience: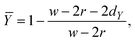
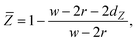
![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) are unit-less quantities that vary from zero to one as the bubble moves from the wall towards the center. Furthermore, it should be noted that the diameter of the bubble is normalized to the channel width:
are unit-less quantities that vary from zero to one as the bubble moves from the wall towards the center. Furthermore, it should be noted that the diameter of the bubble is normalized to the channel width: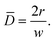
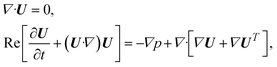
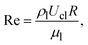
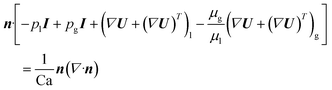
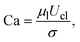
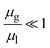 , eqn (6) can be simplified as follows:
, eqn (6) can be simplified as follows: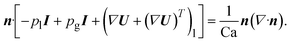
![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) for a thorough computational investigation. Fig. 3 shows the computational setup and results. The velocity of the bubble is monitored as a function of time to make sure that the solution converges to the steady state. To verify the conservation of the bubble's volume, the temporal evolution of the bubble's volume is plotted in Fig. 3e. After verifying that the equilibrium state has been reached, the bubble position and the velocity profile around the bubble are extracted and shown in Fig. 3f and g, respectively.
for a thorough computational investigation. Fig. 3 shows the computational setup and results. The velocity of the bubble is monitored as a function of time to make sure that the solution converges to the steady state. To verify the conservation of the bubble's volume, the temporal evolution of the bubble's volume is plotted in Fig. 3e. After verifying that the equilibrium state has been reached, the bubble position and the velocity profile around the bubble are extracted and shown in Fig. 3f and g, respectively.![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) , and Ca as in experiments. Experimental data are selected for both of the cases where bubbles go to the center or to the wall. Also, data are chosen from two different types of liquids to probe the impact of Ca. The comparison between the two sets of results is summarized in Table 2 with isopropanol as the carrier fluid and Table 3 with ethanol as the carrier fluid. In the tables, Ȳ and
, and Ca as in experiments. Experimental data are selected for both of the cases where bubbles go to the center or to the wall. Also, data are chosen from two different types of liquids to probe the impact of Ca. The comparison between the two sets of results is summarized in Table 2 with isopropanol as the carrier fluid and Table 3 with ethanol as the carrier fluid. In the tables, Ȳ and ![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) are calculated using eqn (1) and (2). At Re ≤ 1.29, the predicted bubble position from the simulations does not correspond to the experimental values. This discrepancy can be explained by considering the possibility that multiple equilibrium positions exist in the channel.33 As a result, it is possible that the simulation chooses one of the equilibrium positions and the experiment the other. More importantly, in the experiments, a row of bubbles can be seen, while a single bubble motion is simulated numerically. At low Re, the range of influence of a bubble increases; promoting inter-bubble interactions that can affect the lateral position of the bubble.43 At higher values of Re and Ca, excellent agreement can be seen between simulations and experiments. Table 4 shows the numerical results for the equilibrium position of the bubbles with different initial positions. The results show that the bubble, starting from different positions, reaches the same equilibrium position. However, this result cannot be considered as a general statement since at low Re, a bubble can possibly have multiple equilibrium positions as seen for solid particles.44
are calculated using eqn (1) and (2). At Re ≤ 1.29, the predicted bubble position from the simulations does not correspond to the experimental values. This discrepancy can be explained by considering the possibility that multiple equilibrium positions exist in the channel.33 As a result, it is possible that the simulation chooses one of the equilibrium positions and the experiment the other. More importantly, in the experiments, a row of bubbles can be seen, while a single bubble motion is simulated numerically. At low Re, the range of influence of a bubble increases; promoting inter-bubble interactions that can affect the lateral position of the bubble.43 At higher values of Re and Ca, excellent agreement can be seen between simulations and experiments. Table 4 shows the numerical results for the equilibrium position of the bubbles with different initial positions. The results show that the bubble, starting from different positions, reaches the same equilibrium position. However, this result cannot be considered as a general statement since at low Re, a bubble can possibly have multiple equilibrium positions as seen for solid particles.44
![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif)
![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) simulation
simulation
![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif)
![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) simulation
simulation
![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) = 0.78
= 0.78![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) = 0.61
= 0.61![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) = 0.82
= 0.82![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) = 0.96
= 0.96![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) = 0.92
= 0.92![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) = 0.51
= 0.51![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) = 0.64
= 0.64![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) = 0.96
= 0.96![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) = 0.78
= 0.78![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) = 0.50
= 0.50![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) = 0.45
= 0.45![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) = 0.93
= 0.93![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) = 0.57
= 0.57![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) = 0.50
= 0.50![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) = 0.4. In each simulation, the bubble's initial position is at (Ȳ,
= 0.4. In each simulation, the bubble's initial position is at (Ȳ, ![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) ) = (0.7667, 0.6). As the Re increases, the bubble moves closer to the wall and at Re larger than 20, the bubble moves to the corner of the channel on the diagonal.
) = (0.7667, 0.6). As the Re increases, the bubble moves closer to the wall and at Re larger than 20, the bubble moves to the corner of the channel on the diagonal.
![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) = 0.4 are shown in Fig. 7. The bubble equilibrium position is closer to the centerline at larger Ca. At Ca higher than 0.9, the bubble moves to the centerline.
= 0.4 are shown in Fig. 7. The bubble equilibrium position is closer to the centerline at larger Ca. At Ca higher than 0.9, the bubble moves to the centerline.
![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) = 0.4 at different combinations of Ca and Re. In the simulations, the bubble is initially positioned at (Ȳ,
= 0.4 at different combinations of Ca and Re. In the simulations, the bubble is initially positioned at (Ȳ, ![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) ) = (0.7667, 0.6) in a square channel. Color coding the equilibrium position of the bubble in Fig. 14 for different Ca and Re values helps to highlight the transition zone of the bubble position from the center to the wall. This figure displays that at high Re, the bubble moves to the wall (small Ȳ) while at high Ca the bubble moves to the centerline (large Ȳ). This diagram helps in predicting the bubble position in the channel under different flow conditions. Analogous diagrams can be drawn for different bubble diameters using the proposed numerical tool.
) = (0.7667, 0.6) in a square channel. Color coding the equilibrium position of the bubble in Fig. 14 for different Ca and Re values helps to highlight the transition zone of the bubble position from the center to the wall. This figure displays that at high Re, the bubble moves to the wall (small Ȳ) while at high Ca the bubble moves to the centerline (large Ȳ). This diagram helps in predicting the bubble position in the channel under different flow conditions. Analogous diagrams can be drawn for different bubble diameters using the proposed numerical tool.

![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) = 0.4 and an initial position of (Ȳ,
= 0.4 and an initial position of (Ȳ, ![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) ) = (0.7667, 0.6) in the channel at different Re and Ca values.
) = (0.7667, 0.6) in the channel at different Re and Ca values.![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) = 0.4 in a square channel and at capillary numbers higher than 0.9, their equilibrium position is at the centerline. Furthermore, bubbles that have a radius smaller than half of the width of the channel move to the wall while bubbles with a radius larger than half of the channel's width move to the centerline. Finally, the comparison between the equilibrium position of a bubble and a solid particle demonstrates that the shallower wall of the rectangular channel is the equilibrium position of the bubble while the solid particle moves to the center of the wider sidewall. This study provides insights into the effective parameters in the bubble motion and the methods we presented can be employed in designing multiphase microfluidic devices. Future studies on the interactions of bubbles introduced from multiple side channels with various sizes will shed more light on the complex dynamics of bubbly flows.
= 0.4 in a square channel and at capillary numbers higher than 0.9, their equilibrium position is at the centerline. Furthermore, bubbles that have a radius smaller than half of the width of the channel move to the wall while bubbles with a radius larger than half of the channel's width move to the centerline. Finally, the comparison between the equilibrium position of a bubble and a solid particle demonstrates that the shallower wall of the rectangular channel is the equilibrium position of the bubble while the solid particle moves to the center of the wider sidewall. This study provides insights into the effective parameters in the bubble motion and the methods we presented can be employed in designing multiphase microfluidic devices. Future studies on the interactions of bubbles introduced from multiple side channels with various sizes will shed more light on the complex dynamics of bubbly flows.













