Landscape of gene networks for random parameter perturbation†
Abstract
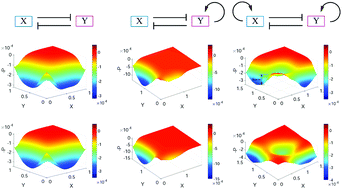
Landscape approaches have been exploited to study the stochastic dynamics of gene networks. However, how to calculate the landscape with a wide range of parameter variations and how to investigate the influence of the network topology on the global properties of gene networks remain to be elucidated. Here, I developed an approach for the landscape of random parameter perturbation (LRPP) to address this issue. Based on a self-consistent approximation approach, by making perturbations to parameters in a given range, I obtained the landscape for gene network systems. I applied this approach to two biological models, one for the mutual repression model and the other for the embryonic stem (ES) cell differentiation network. For the mutual repression model, my results confirm quantitatively that positive feedback promotes the robustness of multistability. For the ES cell differentiation model, I identify three cell states, representing the ES cell, the differentiation cell, and the intermediate state cell, respectively. I propose that the intermediate states and the wide range of parameter values coming from inhomogeneous cellular environments provide possible explanations for the heterogeneity observed in single cell experiments. I also offer a counterintuitive result that noise could reduce heterogeneity and promote the stability of cell states. These results support that the network topology determines the operating principles of the genetic networks, reflected by the representative landscapes from LRPP. This work provides a new route to obtain the potential landscape for a gene network system given a wide range of parameter values and study the influences of the network topology on the global properties of the system.


 Please wait while we load your content...
Please wait while we load your content...