Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Molecular scale structure and dynamics at an ionic liquid/electrode interface†
Peter
Reichert
ab,
Kasper Skov
Kjær
c,
Tim
Brandt van Driel
c,
Julian
Mars
 ab,
Jannis Walther
Ochsmann
a,
Diego
Pontoni
e,
Moshe
Deutsch
ab,
Jannis Walther
Ochsmann
a,
Diego
Pontoni
e,
Moshe
Deutsch
 d,
Martin Meedom
Nielsen
*c and
Markus
Mezger
d,
Martin Meedom
Nielsen
*c and
Markus
Mezger
 *ab
*ab
aMax Planck Institute for Polymer Research, 55128 Mainz, Germany. E-mail: mezger@mpip-mainz.mpg.de
bInstitute of Physics and MAINZ Graduate School, Johannes Gutenberg University Mainz, 55128 Mainz, Germany
cCentre for Molecular Movies, Department of Physics, Technical University of Denmark, DK-2800 Lyngby, Denmark. E-mail: mmee@fysik.dtu.dk
dDepartment of Physics, Institute of Nanotechnology and Advanced Materials, Bar-Ilan University, Ramat-Gan 52900, Israel
eESRF – The European Synchrotron and Partnership for Soft Condensed Matter (PSCM), 38043 Grenoble, France
First published on 27th June 2017
Abstract
After a century of research, the potential-dependent ion distribution at electrode/electrolyte interfaces is still under debate. In particular for solvent-free electrolytes such as room-temperature ionic liquids, classical theories for the electrical double layer are not applicable. Using a combination of in situ high-energy X-ray reflectivity and impedance spectroscopy measurements, we determined this distribution with sub-molecular resolution. We find oscillatory charge density profiles consisting of alternating anion- and cation-enriched layers at both cathodic and anodic potentials. This structure is shown to arise from the same ion–ion correlations dominating the liquid bulk structure. The relaxation dynamics of the interfacial structure upon charging/discharging were studied by impedance spectroscopy and time resolved X-ray reflectivity experiments with sub-millisecond resolution. The analysis revealed three relaxation processes of vastly different characteristic time scales: a 2 ms scale interface-normal ion transport, a 100 ms scale molecular reorientation, and a minute scale lateral ordering within the first layer.
1 Introduction
In the early 20th century Gouy, Chapman and Stern employed the Poisson–Boltzmann equation to describe the spatial ion-distribution of diluted salt solutions near a charged electrode.1–3 However, room-temperature ionic liquids (ILs) consist solely of ions. They are intensively studied as future environmentally-friendly working fluids in applications ranging from catalysis to solar cells and supercapacitors.4 Therefore, the diluted solution approximation is clearly invalid.5–7 Detailed understanding of the function and performance optimization of such devices requires a molecular-resolution knowledge of the electrode’s interfacial structure and its dynamics during the charging/discharging processes.8 Therefore, a variety of experimental, theoretical, and computational techniques have been employed to shed light on the structure and dynamics of ILs near interfaces and in confinement.6For ILs composed of cations with short alkyl side chains, molecular dynamics (MD) simulations suggest an interfacial profile comprising alternating cation- and anion-enriched layers.9 This leads to an oscillatory interfacial concentration profile decaying gradually into the uniform bulk composition. Such profiles deviate significantly from the exponentially decaying concentration profile of a diffuse electric double layer predicted by the classical Gouy–Chapman theory. Furthermore, they cannot be described by the approaches developed for highly concentrated electrolyte solutions and molten salts, taking into account the finite size of ions.10–12 It has been suggested that the observed profiles are a consequence of asymmetric ions13,14 and strong ion–ion correlations in the absence of solvent molecules.15,16
Different experimental techniques have been used to study the molecular-scale structure of ILs at solid/liquid interfaces. Interfacial layering was observed in atomic force microscopy (AFM)17–20 and X-ray reflectivity (XRR) measurements21–24 for several ILs on various substrates. In thin IL films, long range ordered structures have been found by helium atom scattering.25 Starting in 2010, initial attempts have been made to investigate the response of the interfacial structure to electrode potentials by XRR26 and neutron reflectivity.27 However, in these early studies substrate reconstruction on gold surfaces28 and a limited q-range in neutron reflectivity rendered the extraction of the molecular-scale ion structure near the interface highly ambiguous. More recently, different groups have reported synchrotron XRR studies at IL/electrode interfaces under controlled electric potentials.29,30 In all of these studies, distinct changes in the interfacial ion distribution were found upon potential variation. Time resolved experiments, covering the relaxation dynamics on the seconds to minute scale, indicated the presence of ultraslow interfacial processes.31,32 Scanning tunneling microscopy and AFM studies indicate that the substrate-adsorbed cation layer is affected by an applied potential.20,28,33–35 Sum frequency generation (SFG) spectroscopy36 detected molecular reorientations upon variation of the applied potential. Impedance spectroscopy (IS) studies showed that the interfacial dynamics are governed by at least 3 relaxation processes on time scales ranging from milliseconds to minutes.18,20,28 However, based only on these electrochemical studies, it is not possible to unambiguously assign the observed processes to specific spatial rearrangement of ions near the solid/liquid interface.
Here, we present an in situ study of the structure and dynamics of the IL 1-butyl-1-methylpyrrolidinium tris(pentafluoroethyl)trifluorophosphate37 [bmpy]+[FAP]− at an inert electrode during the charging/discharging process. Using high-energy XRR, we determined interface-normal ion profiles with molecular-scale resolution. Comparison with bulk X-ray scattering revealed the origin of the observed spatial ion distribution. Its temporal response to applied potentials was determined by time-resolved XRR and electrochemical IS experiments. This combined approach enabled us for the first time to directly study the structural response of an electrolyte at an electrode on the millisecond to minute time scale.
2 Experimental
2.1 Materials
The IL 1-butyl-1-methylpyrrolidinium tris(pentafluoroethyl)trifluorophosphate [bmpy]+[FAP]− was obtained from Merck in high-purity grade. Pure [bmpy]+[FAP]− can be supercooled well below its melting point of 4 °C, allowing experiments at −12 °C. At this temperature, a liquid mass density of ρm = 1.62 g cm−3 was determined by pycnometry.38 To remove moisture and volatile residues, the IL was kept in a vacuum oven (1 mbar, 90 °C) overnight prior to the experiments.2.2 In situ setup
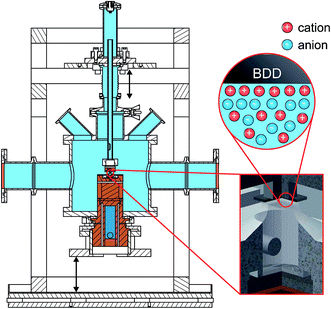
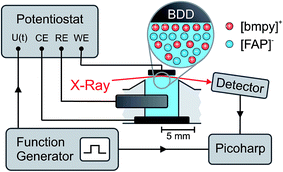
For in situ investigation of the IL/electrode interfaces, a new experimental cell for simultaneous XRR and electrochemical measurements was developed (Fig. 1). The setup is inspired by concepts employed in our previous high energy X-ray reflectivity studies on deeply buried interfaces,21,23,39 and recent developments in the field of electrochemical in situ X-ray scattering techniques.40,41 For visual sample inspection during alignment and measurements in a vacuum or inert atmosphere, the center part of the cell is made of a glass tube (height 140 mm, outer diameter 160 mm, wall thickness 5.5 mm; Schott Duran). For connection with the surrounding stainless steel elements, the glass part is equipped with two DN150 flat flanges (DIN 12214) at the top and bottom. At the side, two KF50 flanges (ISO 2861/1) for the X-ray windows (thickness 50 μm; Kapton) point in the opposite direction. The electrical potential across the solid/liquid interface (Fig. 2) is controlled by a potentiostat in the three electrode configuration (PGSTAT302, Autolab). Using an inert boron doped diamond (BDD) working electrode (WE), we avoid surface reconstruction, which plagues metal electrode measurements.28,42 The working electrode is a monocrystalline BDD plate (size 4 mm × 4 mm × 0.3 mm, boron concentration 1019 cm−3; Element Six) in (100) orientation. A polycrystalline, highly boron doped diamond (electrochemistry grade, boron concentration > 1020 cm−3; Element Six) and a flame annealed 2 mm diameter platinum wire served as the counter electrode and quasi reference electrode, respectively. The solid/liquid interface is formed by touching the BDD electrode to the meniscus of the IL, kept in a temperature controlled PTFE reservoir (Fig. S1†). A 350 μm thick single crystalline corundum plate and a polyether ether ketone spacer electrically isolate the electrochemical cell from the supporting structure. The sample temperature was controlled by a closed cycle thermostat and monitored by two PT-100 sensors underneath the RE and above the WE, respectively. To reduce drifts in the WE/IL interface position, the WE is mechanically decoupled from the lower copper sample post by an aluminum frame and a stainless steel rod.2.3 Impedance spectroscopy (IS)
Impedance spectra for electrode potentials −2.5 V ≤ +1.5 V were recorded in 0.25 V steps under a dry nitrogen atmosphere. For each potential, IS was measured for frequencies between 10 kHz ≥ ω/2π ≥ 0.01 Hz at an excitation voltage of 10 mV.2.4 X-ray reflectivity (XRR)
XRR experiments were performed at the high energy micro diffraction (HEMD) setup at ID15, ESRF (wavelength λ = 0.0178 nm). Details are described elsewhere.38,39,43 After transfer to the measurement chamber, the sample was degassed and kept under helium. This protocol prevents water adsorption, reduces the background signal in XRR measurements, and improves the temperature homogeneity across the sample. X-rays enter and leave the IL through the free standing meniscus formed between the top edge of the PTFE reservoir and the WE. Specular XRR curves R(q) at fixed potentials of +1.5 V, 0 V and −2.5 V were recorded by a single photon counting NaI scintillation detector (Cyberstar CBY48NA05B, Oxford Danfysik). Before each measurement, the interface was equilibrated by applying a 50 Hz oscillatory potential between −2.5 V and +1.5 V. After several minutes the oscillation amplitude was decreased slowly. At the same time, the potential offset was gradually shifted from −0.5 V to its final value. The background, stemming mainly from bulk IL scattering, was collected at a ±0.1° offset in the incidence angle relative to the specular condition. Repeated scans demonstrate that reproducible XRR data up to a scattering angle 2θ = 1.8° can be attained while keeping the radiation damage of the sample at an acceptable level. The specular and background signals from multiple scans were averaged and interpolated to a regular grid in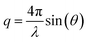 , where θ is the X-rays’ grazing angle of incidence with respect to the interface and 2θ is the total scattering angle. After background subtraction, footprint corrections were applied to account for the finite beam and sample sizes.
, where θ is the X-rays’ grazing angle of incidence with respect to the interface and 2θ is the total scattering angle. After background subtraction, footprint corrections were applied to account for the finite beam and sample sizes.
2.5 Time resolved experiments
Time resolved XRR signals were recorded at a fixed incidence angle θ = 0.35°, corresponding to a momentum transfer q = 4.3 nm−1. At this angle, excellent counting statistics were obtained. To study slow processes on the minute time scale, cyclic voltammetry (CV) between −2.5 V and +1.6 V was performed at a scanning speed of 10 mV s−1. Fast processes were investigated by monitoring the relaxation of the XRR signal during periodic square wave potential cycles44,45 (Fig. 2). Alternating steps between −2.5 V and +1.6 V with 0.02 μs rise time were applied to the WE at a frequency of 50 Hz. Each single photon counting event, recorded by the X-ray detector, was logged by a Picoharp (PicoQuant). Sub-millisecond time resolution was achieved by calculating the histogram of counting events recorded over several minutes vs. delay with respect to the rising edge of the potential steps.2.6 Bulk X-ray scattering
Bulk X-ray scattering was measured in the transmission geometry on a self constructed instrument using Cu Kα radiation (λKα = 0.154 nm, Rigaku MicroMax 007 microfocus rotating anode X-ray generator, Osmic Max-Flux confocal multilayer optics).46 A 1 mm thick [bmpy]+[FAP]− sample was contained between two diamond windows to suppress background scattering. Diffraction patterns were obtained by azimuthal integration of the data recorded on a 2D image plate detector (Mar345, MarResearch) at a sample-detector distance of 342 mm and applying standard correction factors.473 Analysis
3.1 X-ray reflectivity
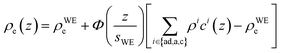 | (1) |
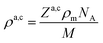 | (2) |
Originally, the profile normal to the solid/liquid interface was composed of ionic contributions from cations (c), anions (a), and the working electrode ρWEe. This model was extended to account for the excess charge of the surface-adsorbed (ad) ion layer cad, controlled by the applied potential. The partial electron densities ρa,c are calculated from the composition of the respective ion species (eqn (2)). Za,c is the number of electrons per anion/cation, ρm the IL bulk mass density, M the molecular mass of the IL, and NA the Avogadro constant. Following Névot and Croce, the cumulative normal distribution function
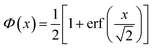 | (3) |
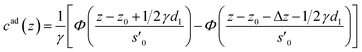 | (4) |
The distance z0 controls the separation of the adsorbed layer from the electrode. A full monolayer of adsorbed ions corresponds to an area density ρaddI. As motivated by the work of Fedorov et al.,5 the dimensionless parameter γ limits the maximum local ion concentration within the adsorbed layer to cad(z) < 1/γ. The slab thickness Δz was set to obey charge neutrality. It is determined by the surface charge σ(U) and calculated numerically by the condition
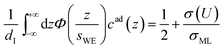 | (5) |
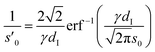 | (6) |
Eqn (6) is calculated from the constraint that at the surface charge σ(U) = 1/2σML the area and maximum value of cad(z) agree with the corresponding Gaussian density distribution for n = 0.
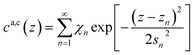 | (7a) |
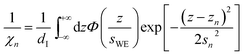 | (7b) |
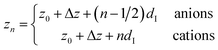 | (7c) |
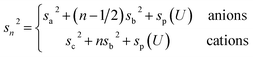 | (7d) |
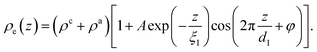 | (8) |
Here, the oscillatory profile adjacent to the solid/liquid interface is solely characterized by its amplitude A, phase φ, periodicity dI, and decay length ξI.
For sufficiently large z/dI, the profiles calculated by eqn (7) exhibit the asymptotic behavior predicted by eqn (8).38,60 Therefore, the effective parameters for the periodicity dI and correlation length ξI of the oscillatory interfacial structures were numerically determined from the anion and cation contributions to the total electron density profiles.
3.2 Impedance spectroscopy
For IS, a small sinusoidal potential variation with frequency ω/(2π) is applied to a capacitor in equilibrium at a constant potential U. The measured complex capacitance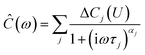 | (9) |
4 Results and discussion
4.1 Surface charge
The impedance spectra (Fig. 3) reveal two distinct capacitive processes on different time scales τj and with different relaxation strengths ΔCj, each represented by a half circle in the complex capacitance plane (Fig. 4). At low frequencies, the onset of a third slow process is observed. With the total differential capacitance ΔC(U), the surface charge difference on the electrode Δσ(U) can be obtained by numerical integration.| C(U) = ΔC1(U) + ΔC2(U) | (10) |
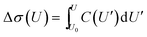 | (11) |
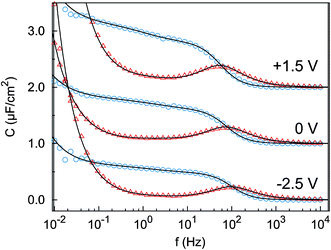 | ||
| Fig. 3 Imaginary part (red triangles) and real part (blue circles) of the complex differential capacitance at the potentials +1.5 V (top), 0 V (middle) and −2.5 V (bottom). Lines are fits to the Cole–Cole expression (eqn (9)). Curves are vertically shifted by 1 unit for clarity. | ||
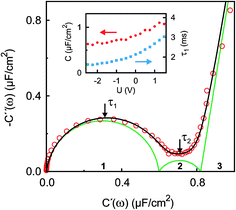 | ||
| Fig. 4 Experimental IS data in the complex capacitance plane Ĉ(ω) = C′(ω) + iC′′(ω) at U = 0 V (open circles) in the frequency range 10 kHz ≥ ω/2π ≥ 0.01 Hz. The black line is a fit to eqn (9). Green lines indicate contributions of the three numbered individual processes. Arrows point to frequencies corresponding to the relaxation times τ1 ≈ 2 ms and τ2 ≈ 120 ms. The inset shows the potential dependence of the differential capacitance C (red circles) and the relaxation time τ1 (blue squares) of the fast process. | ||
The surface charge difference relative to U0 = 0 V was calculated as Δσ(+1.5 V) = 1.8 μC cm−2 and Δσ(−2.5 V) = −1.9 μC cm−2. This amounts to approx. ±10% of a cation monolayer, having a surface charge of σML = 19 μC cm−2. The reduced capacitance of the [bmpy]+[FAP]−/BDD interface, compared to gold electrodes,18 is a consequence of the relatively low free charge carrier density of the semiconducting BDD working electrode.
4.2 Ion profile
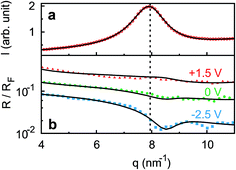
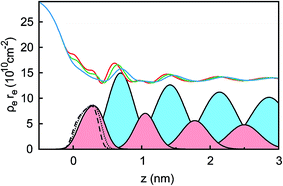
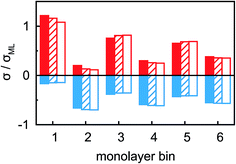
Ion distributions normal to the interface were studied by XRR at fixed potentials. To highlight changes induced by rearrangement of cations and anions, the experimental XRR patterns R(q) were normalized by the Fresnel reflectivity RF(q) of an ideally flat and abrupt IL/BDD interface (Fig. 5b). The −2.5 V XRR curve shows a pronounced dip at q ≈ 8 nm−1, corresponding to a distance of 2π/q ≈ 0.8 nm. Its position and width are close to those of the first scattering peak of the bulk liquid (Fig. 5a). Quantitative analysis by Fourier transformation of the total structure function yield a bulk periodicity dB = 0.80 nm and a bulk correlation length ξB = 1.46 nm.38 Bulk X-ray and neutron scattering measurements as well as MD simulations on similar ILs suggest that this periodicity corresponds to the average bulk separation between same-charge ions.16,63–66 Increasing the potential from −2.5 V to +1.5 V results in an almost structureless XRR pattern. Compared to XRR curves measured at IL/gold interfaces,26 the signal modulations in this study are significantly enhanced. This results from a better scattering contrast between diamond and the IL than that between Au and the IL, demonstrating the high sensitivity of our method for detecting potential-induced ion rearrangement near the electrode.For a quantitative interpretation, the measured XRR curves were fitted by the modified distorted crystal model described in Section 3.1. All three measured XRR curves recorded at different potentials were fitted simultaneously with the same values for all bulk-related parameters, the same surface roughness of the BDD working electrode, and the fixed surface charge difference Δσ(U), determined by IS. The XRR fits (lines in Fig. 5b) yield layered density profiles for both the anion and cation (Fig. 6). The resultant effective interfacial layer periodicity dI = 0.73 nm and the decay length ξI = 1.44 nm are in accordance with the XRR measurements on negatively charged sapphire substrates,21,38 and AFM measurements that revealed a layer periodicity of 0.9 nm.28 The good correspondence between dI and dB as well as ξI and ξB indicates that the interfacial structure is governed by the same ion–ion correlations dominating the bulk structure.23,51,58,67 The ion concentrations in each layer (Fig. 7) were determined by integration of the interfacial model profiles, derived from the XRR fits.
The interfacial profiles agree qualitatively with the results from MD simulations and continuum theory at comparable surface charges.9,15 In comparison with the parameters used in the continuum theory model, in our system the normalized bulk correlation length ξB/dB is four times larger. This leads to stronger oscillations in the relative cation/anion concentrations. A cation excess was found in the substrate adsorbed layer at all three potentials. At +1.5 V, the surface charge, i.e. the sum over all layers, amounts to an equivalent of approx. 60% of the charge in a cation monolayer. Thus, the potential of zero charge must occur at high anodic potentials, where a maximum in C(U) is predicted for symmetric ions.12,15 This is in agreement with the observation of a monotonically increasing C(U) between a potential of −2.5 V and +1.5 V (Fig. 4 inset).
Our choice of a chemically inert but semiconducting BDD electrode material leads to an exponential charge carrier density profile within the working electrode.68 This limits the surface charge difference between −2.5 V and +1.5 V to approx. 20% of a cation monolayer. Therefore, in our experiments neither the potential of zero charge followed by the exchange of cations with anions in the adsorbed layer, nor lattice saturation and the crowding regime, is reached.69–71 However, the observed potential dependent XRR patterns are fully reversible and reproducible. In contrast to a recent study by the group of P. Dutta using silicon working electrodes,32 no formation of extended, several nanometer thick interfacial adsorbed layers were observed in this study.
Two main features of ion density profiles were found to vary significantly with applied potential. The first is the center of mass of the substrate-adsorbed layers. At +1.5 V the center is observed at 0.20 nm. For more negative potentials, the center is shifting away from the electrode surface. At 0 V we find a separation of 0.23 nm and at −2.5 V a value of 0.28 nm. Similar shifts in the substrate-adsorbed layer position were observed in AFM force–distance curves.28,34,35
Moving away from the electrode, details related to the specific molecular organization of the cations in the adsorbed layer become indistinguishable. At these larger distances z, the oscillatory density profiles are solely characterized by their effective amplitudes, phases φ, periodicities dI, and decay lengths ξI (eqn (8)). The latter two are linked to their corresponding bulk values dB and ξB, respectively.38,59,72 Therefore, these two parameters are expected to remain unchanged upon potential variation. However, changes in the adsorbed layer result in phase shifts of the IL’s oscillatory profile relative to the solid electrode (eqn (8) and Fig. 6). The XRR signal R(q)/RF(q) originates from the interference of waves reflected at gradients in the interfacial electron density profiles. Therefore, XRR is highly sensitive to such phase shifts. Demonstratively, phase shifts in the oscillatory profile lead to different interference patterns with the waves reflected from the BDD electrode having an electron density about twice the IL bulk value (Fig. 6 and S2†). These interference effects explain the strong variation of the XRR signal at different potentials despite the rather small changes in the charge concentrations in all layers, shown in Fig. 7.
4.3 Interfacial dynamics
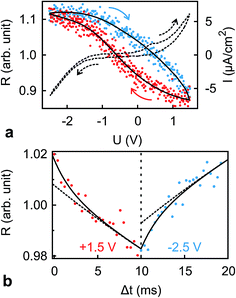
The dynamics of ion rearrangement at the IL/electrode interface during the charging/discharging process were studied by combining the IS measurements (Fig. 4) with two complementary time-resolved XRR measurements. The first, yielding sub-millisecond time resolution, recorded the evolution of the XRR signal at a fixed q following an abrupt positive/negative switching of the potential U(t) (Fig. 8b). The second, providing information on a longer time scale, recorded the evolution of the same fixed-q XRR signal during a slow cyclic voltammetry (CV) scan U(t) (Fig. 8a). Thus, the structural rearrangement of cations and anions adjacent to the electrode during the charging/discharging process was investigated on time scales spanning several orders of magnitudes.In the abrupt switching measurements, a periodic square wave potential with 4 V steps and 0.02 μs rise time were applied to the IL/electrode interface while recording XRR. The resultant XRR signal shows a small but significant modulation with a relative amplitude of approx. 2%. Relaxation times were determined by fitting the measured XRR with a sum of two decaying exponentials and a constant baseline.
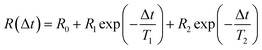 | (12) |
To extract the long relaxation time T2 of the slow component from 50 Hz cycles, R0 = R(Δt → ∞) was fixed to the values determined from the static XRR curves at q = 4.3 nm−1 (Fig. 5b).
The fit (Fig. 8b) yields T1 = 2 ms in good agreement with the relaxation time τ1 ≈ 2 ms of the first, fast, process observed above by IS. The fits by eqn (9) to the IS data yield a value for α1 of 0.93. This is close to unity as expected for diffusion driven electrode polarization.62 Furthermore, on Au electrodes, a Vogel–Fulcher-like temperature dependence was found for this relaxation process.18 Such dependence is characteristic of the bulk ion conductivity, suggesting that the fast relaxation process is connected to ion transport from/to the interface, limited by the ion conductivity. Indeed, its capacitive strength, ΔC1 ≈ 0.6 μF cm−2, dominates the total capacitance found by IS (Fig. 4) and supports this interpretation.
The magnitude R2 of the intensity modulations associated with the second exponential (dashed lines in Fig. 8b) is more than an order of magnitude larger than R1. Our model fits of the XRR curves, recorded at different static potentials, show that these large modulations primarily originate from shifts of the first cation layer normal to the electrode surface. SFG spectroscopy suggests such shifts to result from potential-dependent reorientations of the asymmetric [bmpy]+ substrate-adsorbed cations.36 The corresponding relaxation time T2 = 50 ms is less than half of τ2 ≈ 120 ms of the second relaxation process observed by IS. However, the time scales are of the same order of magnitude. The difference may arise from the specific experimental conditions. In IS an equilibrated system is probed by small perturbations. In contrast, for the fast XRR measurements potential steps of 4 V are applied to the IL/electrode interface. This leads to a highly non-equilibrium ion configuration and a relaxation pathway with a faster time constant T2. Apparently, this reorientation is governed by specific ion–electrode interactions and happens on much longer time scales T2 than the ion transport. The broad relaxation time distribution obtained from IS with α2 ≈ 0.6 may reflect electrode surface inhomogeneities. The Arrhenius-like temperature dependence of τ2 found on gold electrodes18 supports our assignment of this process to molecular reorientation within the first adsorbed cation layer. Finally, note that compared to the fast ion transport process, the slower reorientation process has only a small capacitive strength ΔC2 of approx. 0.2 μF cm−2. This may arise from the relaxation of the first cation layer’s distance from the electrode surface, as well as the adsorption of additional cations on vacancies formed after reorientation.
In the low frequency regime, i.e. on the time scale above 10 s, the IS data (Fig. 4) indicates the onset of a third, very slow, process. This agrees with the existence of a hysteresis loop in the XRR signal recorded during CV (Fig. 8a). The presence of such a loop confirms the occurrence of structural rearrangements on a time scale over which a significant potential variation is affected in a CV scan, i.e. 10–100 s. Such slow dynamics could be caused by a lateral reorganization and eventually 2D ordering of the first layer of interface-adsorbed cations, as observed in scanning tunneling microscopy33 that also shows very slow dynamics upon potential variation.73 Likewise, in XRR studies on electrified IL/graphene interfaces, relaxation times on the 10 s scale have been observed.29,31 Here, the slow dynamics was attributed to the presence of a bistable system with a large energy barrier of approx. 9kBT. The stable states are represented by the structures having either an anion or cation layer adsorbed on the electrode. However, our combined IS and XRR study shows that the ion transport to and from the interface occurs on a much faster millisecond time scale.
5 Summary and conclusions
In conclusion, combining electrochemical and time-resolved XRR and IS measurements, we presented a comprehensive picture of the molecular-scale structure of an IL/electrode interface. Its response to applied potential comprises multiple time scales ranging from a few milliseconds to hundreds of seconds. At all investigated potentials the interface-normal ion concentration profiles exhibit a distinct layering structure. The measured XRR curves are reproduced by a single layering periodicity and a single decay length which are independent of the applied potential. They are close to those of the bulk correlation, implying that bulk correlations dominate also the interfacial structure. The time-resolved measurements suggest a three-step structure-variation scenario for the charging/discharging process at an IL/electrode interface (Fig. 9). Specifically, switching the voltage from −2.5 V to +1.5 V reduces the surface charge by approx. 20% of a monolayer-equivalent. The diffusion-limited ion transport from and to the interface happens on a millisecond time scale. In addition, a shift occurs in the first cation layer’s position relative to the electrode surface. This process exhibits a small capacitive strength and slow relaxation time on the order of 100 ms. We tentatively assign this process to a reorientation of substrate-adsorbed cations. Due to ion–electrode interactions, this reorientation process is strongly hindered and sensitive to electrode inhomogeneities. These inhomogeneities lead to a broad relaxation time distribution. Finally, based on observations by scanning probe techniques,33,73 we suggest that the even slower third process, observed in CV on the 10–100 s time scale, is related to a lateral reorganization of substrate-adsorbed cations. However, at deeply-buried solid/liquid interfaces such processes can not be probed directly by grazing-incidence X-ray diffraction due to the intrinsically strong background originating from the IL bulk.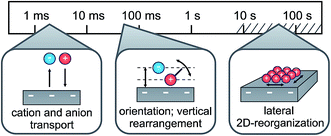 | ||
| Fig. 9 Schematic representation of the three relaxation processes during charging/discharging of the IL/electrode interface, along with their associated time scales. | ||
Acknowledgements
The expert advice and assistance of Veijo Honkimäki at beamline ID15, ESRF, is gratefully acknowledged. This work was supported by the German-Israeli Foundation for Scientific Research and Development (No. 2306-2310.14/2011). PR and JM are recipients of a fellowship funded through the Excellence Initiative (DFG/GSC 266). KSK, TBvD, and MMN acknowledge support from the Danish National Research Foundation, the Danish Strategic Research Council through the project ‘ReLiable’, and from DANSCATT. Open Access funding provided by the Max Planck Society.References
- M. Gouy, J. Phys. Theor. Appl., 1910, 9, 457–468 CrossRef.
- D. L. Chapman, Philos. Mag., 1913, 25, 475–481 Search PubMed.
- O. Stern, Z. Elektrochem. Angew. Phys. Chem., 1924, 30, 508–516 CAS.
- P. Simon and Y. Gogotsi, Nat. Mater., 2008, 7, 845–854 CrossRef CAS PubMed.
- M. V. Fedorov and A. A. Kornyshev, Electrochim. Acta, 2008, 53, 6835–6840 CrossRef CAS.
- M. V. Fedorov and A. A. Kornyshev, Chem. Rev., 2014, 114, 2978–3036 CrossRef CAS PubMed.
- A. Kornyshev and R. Qiao, J. Phys. Chem. C, 2014, 118, 18285–18290 CAS.
- S. Kondrat, P. Wu, R. Qiao and A. A. Kornyshev, Nat. Mater., 2014, 13, 387 CrossRef CAS PubMed.
- R. M. Lynden-Bell, M. G. Del Pópolo, T. G. A. Youngs, J. Kohanoff, C. G. Hanke, J. B. Harper and C. C. Pinilla, Acc. Chem. Res., 2007, 40, 1138–1145 CrossRef CAS PubMed.
- V. Freise, Z. Elektrochem., 1952, 56, 822–827 CAS.
- M. Rovere and M. P. Tosi, Rep. Prog. Phys., 1986, 49, 1001 CrossRef CAS.
- A. A. Kornyshev, J. Phys. Chem. B, 2007, 111, 5545–5557 CrossRef CAS PubMed.
- M. Fedorov, N. Georgi and A. Kornyshev, Electrochem. Commun., 2010, 12, 296–299 CrossRef CAS.
- N. Georgi, A. A. Kornyshev and M. V. Fedorov, J. Electroanal. Chem., 2010, 649, 261–267 CrossRef CAS.
- M. Z. Bazant, B. D. Storey and A. A. Kornyshev, Phys. Rev. Lett., 2011, 106, 046102 CrossRef PubMed.
- H. K. Kashyap, C. S. Santos, H. V. R. Annapureddy, N. S. Murthy, C. J. Margulis and E. W. Castner Jr, Faraday Discuss., 2011, 154, 133–143 RSC.
- R. Atkin and G. Warr, J. Phys. Chem. C, 2007, 111, 5162–5168 CAS.
- M. Drüschler, N. Borisenko, J. Wallauer, C. Winter, B. Huber, F. Endres and B. Roling, Phys. Chem. Chem. Phys., 2012, 14, 5090–5099 RSC.
- H. Li, R. Wood, F. Endres and R. Atkin, J. Phys.: Condens. Matter, 2014, 26, 284115 CrossRef PubMed.
- R. Atkin, N. Borisenko, M. Drüschler, F. Endres, R. Hayes, B. Huber and B. Roling, J. Mol. Liq., 2014, 192, 44–54 CrossRef CAS.
- M. Mezger, H. Schröder, H. Reichert, S. Schramm, J. S. Okasinski, S. Schöder, V. Honkimäki, M. Deutsch, B. M. Ocko, J. Ralston, M. Rohwerder, M. Stratmann and H. Dosch, Science, 2008, 322, 424–428 CrossRef CAS PubMed.
- H. Zhou, M. Rouha, G. Feng, S. S. Lee, H. Docherty, P. Fenter, P. T. Cummings, P. F. Fulvio, S. Dai, J. McDonough, V. Presser and Y. Gogotsi, ACS Nano, 2012, 6, 9818–9827 CrossRef CAS PubMed.
- M. Mezger, S. Schramm, H. Schröder, H. Reichert, M. Deutsch, E. J. De Souza, J. S. Okasinski, B. M. Ocko, V. Honkimäki and H. Dosch, J. Chem. Phys., 2009, 131, 094701 CrossRef PubMed.
- Z. Brkljaca, M. Klimczak, Z. Milicevic, M. Weisser, N. Taccardi, P. Wasserscheid, D. M. Smith, A. Magerl and A. S. Smith, J. Phys. Chem. Lett., 2015, 6, 549 CrossRef CAS PubMed.
- E. M. McIntosh, J. Ellis, A. P. Jardine, P. Licence, R. G. Jones and W. Allison, Chem. Sci., 2014, 5, 667–676 RSC.
- R. Yamamoto, H. Morisaki, O. Sakata, H. Shimotani, H. Yuan, Y. Iwasa, T. Kimura and Y. Wakabayashi, Appl. Phys. Lett., 2012, 101, 053122 CrossRef.
- Y. Lauw, T. Rodopoulos, M. Gross, A. Nelson, R. Gardner and M. D. Horne, Rev. Sci. Instrum., 2010, 81, 074101 CrossRef CAS PubMed.
- R. Atkin, N. Borisenko, M. Drüschler, S. Z. El Abedin, F. Endres, R. Hayes, B. Huber and B. Roling, Phys. Chem. Chem. Phys., 2011, 13, 6849 RSC.
- A. Uysal, H. Zhou, G. Feng, S. S. Lee, S. Li, P. Fenter, P. T. Cummings, P. F. Fulvio, S. Dai, J. K. McDonough and Y. Gogotsi, J. Phys. Chem. C, 2014, 118, 569–574 CAS.
- T. A. Petach, A. Mehta, R. Marks, B. Johnson, M. F. Toney and D. Goldhaber-Gordon, ACS Nano, 2016, 10, 4565 CrossRef CAS PubMed.
- A. Uysal, H. Zhou, G. Feng, S. S. Lee, S. Li, P. T. Cummings, P. F. Fulvio, S. Dai, J. K. McDonough, Y. Gogotsi and P. Fenter, J. Phys.: Condens. Matter, 2015, 27, 032101 CrossRef PubMed.
- M. Chu, M. Miller, T. Douglas and P. Dutta, J. Phys. Chem. C, 2017, 121, 3841 CAS.
- Y.-Z. Su, Y.-C. Fu, J.-W. Yan, Z.-B. Chen and B.-W. Mao, Angew. Chem., Int. Ed., 2009, 48, 5148–5151 CrossRef CAS PubMed.
- X. Zhang, Y.-X. Zhong, J.-W. Yan, Y.-Z. Su, M. Zhang and B.-W. Mao, Chem. Commun., 2012, 48, 582 RSC.
- J. M. Black, D. Walters, A. Labuda, G. Feng, P. C. Hillesheim, S. Dai, P. T. Cummings, S. V. Kalinin, R. Proksch and N. Balke, Nano Lett., 2013, 13, 5954–5960 CrossRef CAS PubMed.
- S. Baldelli, Acc. Chem. Res., 2008, 41, 421–431 CrossRef CAS PubMed.
- N. V. Ignat’ev, U. Welz-Biermann, A. Kucheryna, G. Bissky and H. Willner, J. Fluorine Chem., 2005, 126, 1150–1159 CrossRef.
- M. Mezger, R. Roth, H. Schröder, P. Reichert, D. Pontoni and H. Reichert, J. Chem. Phys., 2015, 142, 164707 CrossRef PubMed.
- M. Mezger, S. Schöder, H. Reichert, H. Schröder, J. Okasinski, V. Honkimäki, J. Ralston, J. Bilgram, R. Roth and H. Dosch, J. Chem. Phys., 2008, 128, 244705 CrossRef PubMed.
- F. U. Renner, Y. Gründer and J. Zegenhagen, Rev. Sci. Instrum., 2007, 78, 033903 CrossRef PubMed.
- B. M. Murphy, M. Greve, B. Runge, C. T. Koops, A. Elsen, J. Stettner, O. H. Seeck and O. M. Magnussen, J. Synchrotron Radiat., 2014, 21, 45–56 CrossRef CAS PubMed.
- B. M. Ocko, J. Wang, A. Davenport and H. Isaacs, Phys. Rev. Lett., 1990, 65, 1466 CrossRef CAS PubMed.
- H. Reichert, V. Honkimäki, A. Snigirev, S. Engemann and H. Dosch, Phys. B, 2003, 336, 46–55 CrossRef CAS.
- J. DeVilbiss, J. Wang, B. Ocko, K. Tamura, R. Adzic, I. Vartanyants and I. Robinson, Electrochim. Acta, 2002, 47, 3057–3064 CrossRef CAS.
- K. Tamura, J. X. Wang, R. R. Adzic and B. M. Ocko, J. Phys. Chem. B, 2004, 108, 1992–1998 CrossRef CAS.
- H. Weiss, J. Mars, H. Li, G. Kircher, O. Ivanova, A. Feoktystov, O. Soltwedel, M. Bier and M. Mezger, J. Phys. Chem. B, 2017, 121, 620–629 CrossRef CAS PubMed.
- L. B. Skinner, C. J. Benmore and J. B. Parise, Nucl. Instrum. Methods Phys. Res., Sect. A, 2012, 662, 61–70 CrossRef CAS.
- M. J. Regan, E. H. Kawamoto, S. Lee, P. S. Pershan, N. Maskil, M. Deutsch, O. M. Magnussen, B. M. Ocko and L. E. Berman, Phys. Rev. Lett., 1995, 75, 2498–2501 CrossRef CAS PubMed.
- O. M. Magnussen, B. M. Ocko, M. J. Regan, K. Penanen, P. S. Pershan and M. Deutsch, Phys. Rev. Lett., 1995, 74, 4444–4447 CrossRef CAS PubMed.
- P. S. Pershan and M. Schlossman, Liquid Surfaces and Interfaces: Synchrotron X-ray Methods, Cambridge University Press, 2012 Search PubMed.
- M. Mezger, B. M. Ocko, H. Reichert and M. Deutsch, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 3733–3737 CrossRef CAS PubMed.
- L. Nevot and P. Croce, Rev. Phys. Appl., 1980, 15, 761–779 CrossRef CAS.
- M. Tolan, X-ray scattering from soft-matter thin films: materials science and basic research, Springer, Berlin, 1999, vol. 148 Search PubMed.
- L. G. Parratt, Phys. Rev., 1954, 95, 359–369 CrossRef.
- C. T. Chantler, K. Olsen, R. A. Dragoset, A. R. Kishore, S. A. Kotochigova and D. S. Zucker, X-Ray Form Factor, Attenuation and Scattering Tables, National Institute of Standards and Technology, Gaithersburg, 2003 Search PubMed.
- L. Ingber, Math. Comput. Modell., 1993, 18, 29–57 CrossRef.
- M. E. Fisher and B. Wiodm, J. Chem. Phys., 1969, 50, 3756–3772 CrossRef CAS.
- C. Grodon, M. Dijkstra, R. Evans and R. Roth, Mol. Phys., 2005, 103, 3009–3023 CrossRef CAS.
- J.-P. Hansen and I. R. McDonald, Theory of simple liquids, Academic Press, Oxford, 2013 Search PubMed.
- M. J. Regan, P. S. Pershan, O. M. Magnussen, B. M. Ocko, M. Deutsch and L. E. Berman, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 15874–15884 CrossRef CAS.
- K. S. Cole and R. H. Cole, J. Chem. Phys., 1941, 9, 341–351 CrossRef CAS.
- R. Coelho, J. Non-Cryst. Solids, 1991, 131–133, 1136–1139 CrossRef.
- C. S. Santos, N. S. Murthy, G. A. Baker and E. W. Castner Jr, J. Chem. Phys., 2011, 134, 121101 CrossRef PubMed.
- C. Hardacre, J. D. Holbrey, C. L. Mullan, T. G. A. Youngs and D. T. Bowron, J. Chem. Phys., 2010, 133, 074510 CrossRef PubMed.
- J. J. Hettige, H. K. Kashyap, H. V. R. Annapureddy and C. J. Margulis, J. Phys. Chem. Lett., 2013, 4, 105–110 CrossRef CAS PubMed.
- J. C. Araque, J. J. Hettige and C. J. Margulis, J. Phys. Chem. B, 2015, 119, 12727–12740 CrossRef CAS PubMed.
- R. Evans and R. J. F. Leote de Carvalho, in Chemical Applications of Density-Functional Theory, ed. B. B. Laird, R. B. Ross and T. Ziegler, American Chemical Society, Washington, DC, 1996, vol. 629, pp. 166–184 Search PubMed.
- M. M. Islam, M. T. Alam, T. Okajima and T. Ohsaka, J. Phys. Chem. C, 2009, 113, 3386–3389 CAS.
- M. M. Islam, M. T. Alam and T. Ohsaka, J. Phys. Chem. C, 2008, 112, 16568–16574 CAS.
- J. Vatamanu, O. Borodin and G. D. Smith, J. Phys. Chem. B, 2011, 115, 3073–3084 CrossRef CAS PubMed.
- J. Vatamanu, O. Borodin, D. Bedrov and G. D. Smith, J. Phys. Chem. C, 2012, 116, 7940–7951 CAS.
- G. A. Martynov, Fundamental theory of liquids: method of distribution functions, Hilger, Bristol, 1992 Search PubMed.
- F. Endres, N. Borisenko, S. Z. E. Abedin, R. Hayes and R. Atkin, Faraday Discuss., 2011, 154, 221–233 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Details of the electrochemical cell and model calculations of XRR patterns. See DOI: 10.1039/c7fd00171a |
| This journal is © The Royal Society of Chemistry 2018 |